Властивостi лiнiйних операторiв та iх застосування при розвтАЩязаннi задач. Матриця лiнiйного оператора
КУРСОВА РОБОТА
"Властивостi лiнiйних операторiв та iх застосування при розвтАЩязаннi задач. Матриця лiнiйного оператора"
Запорiжжя 2010
1. Поняття лiнiйного оператора. Алгебраiчнi операцii над операторами
Нехай ![]() Ваi
Ваi ![]() Вадва рiзних лiнiйних простору над полем комплексних чисел. Вiдображення
Вадва рiзних лiнiйних простору над полем комплексних чисел. Вiдображення ![]() , яке ставляi у вiдповiднiсть кожному вектору
, яке ставляi у вiдповiднiсть кожному вектору ![]() Вапростору
Вапростору ![]() Вадеякий вектор
Вадеякий вектор ![]() Вапростору
Вапростору ![]() , будемо називати оператором
, будемо називати оператором ![]() , дiючий iз
, дiючий iз ![]() Вав
Вав ![]() . Якщо
. Якщо ![]() Ваi образом вектора
Ваi образом вектора ![]() , то пишуть
, то пишуть ![]() .
.
Оператор ![]() Ваназиваiться лiнiйним, якщо виконуються двi умови:
Ваназиваiться лiнiйним, якщо виконуються двi умови:
1. ![]() Ва(властивiсть адитивностi);
Ва(властивiсть адитивностi);
2. ![]() Ва(властивiсть однорiдностi);
Ва(властивiсть однорiдностi);
Тут ![]() довiльно взятi вектори простору
довiльно взятi вектори простору ![]() ,
, ![]() довiльно комплексне число.
довiльно комплексне число.
Позначимо через ![]() Вамножина всiх лiнiйних операторiв, дiючих iз
Вамножина всiх лiнiйних операторiв, дiючих iз ![]() Вав
Вав ![]() . Два лiнiйних оператора
. Два лiнiйних оператора ![]() Ваi
Ваi ![]() Вабудемо вважати рiвними, якщо для будь тАУ якого вектору
Вабудемо вважати рiвними, якщо для будь тАУ якого вектору ![]() Вапростору
Вапростору ![]() . Визначимо тепер операцiю додавання iз множини
. Визначимо тепер операцiю додавання iз множини ![]() Ваi операцiю множення оператора на число. Пiд сумою двох лiнiйних операторiв
Ваi операцiю множення оператора на число. Пiд сумою двох лiнiйних операторiв ![]() Ваi
Ваi ![]() Варозумiють оператор
Варозумiють оператор ![]() Ватакий, що для будь тАУ якого вектора
Ватакий, що для будь тАУ якого вектора ![]() Вапростору
Вапростору ![]()
![]() .
.
Пiд добутком лiнiйного оператора ![]() Вана комплексне число
Вана комплексне число ![]() Варозумiють оператор
Варозумiють оператор ![]() Ватакий, що для любого вектора
Ватакий, що для любого вектора ![]() Вапростору
Вапростору ![]()
![]()
Неважко переконатися в тому, що оператори ![]() Ваi
Ваi ![]() Валiнiйнi.
Валiнiйнi.
Оператор ![]() Ваназиваiться нульовим, якщо для будь тАУ якого вектору
Ваназиваiться нульовим, якщо для будь тАУ якого вектору ![]() Вапростору
Вапростору ![]()
![]() .
.
Щоб переконатися, що оператор ![]() Валiнiйний i, як наслiдок, належностi множинi
Валiнiйний i, як наслiдок, належностi множинi ![]() , потрiбно показати, що для довiльно взятих векторiв
, потрiбно показати, що для довiльно взятих векторiв ![]() Вапростору
Вапростору ![]() Вамають мiсце рiвностi
Вамають мiсце рiвностi ![]() Ваi
Ваi ![]() . Так як будь тАУ якому вектору простору
. Так як будь тАУ якому вектору простору ![]() Ваоператор
Ваоператор ![]() Ваставить у вiдповiднiсть вектор
Ваставить у вiдповiднiсть вектор ![]() , то
, то ![]()
![]() . Як наслiдок,
. Як наслiдок, ![]() - лiнiйний оператор.
- лiнiйний оператор.
Введемо поняття оператора, протилежному лiнiйному оператору ![]() . Оператор тАУ
. Оператор тАУ ![]() Ваназиваiться протилежним оператором
Ваназиваiться протилежним оператором ![]() , якщо
, якщо ![]() . Неважко перевiрити, що для довiльно взятого оператору
. Неважко перевiрити, що для довiльно взятого оператору ![]() Ваiз
Ваiз ![]() Ваi що
Ваi що ![]() Валiнiйний оператор.
Валiнiйний оператор.
Введенi на множинi ![]() Валiнiйнi операцii над ii елементами (операторами) мають такi властивостi:
Валiнiйнi операцii над ii елементами (операторами) мають такi властивостi:
1.![]() ,
,
2. ![]() ,
,
3. iснуi один лiнiйний оператор ![]() Ватакий, що для будь тАУ якого лiнiйного оператора
Ватакий, що для будь тАУ якого лiнiйного оператора ![]() Ваiз
Ваiз ![]()
![]()
4. для кожного оператора ![]() Ваiснуi iдиний оператор тАУ
Ваiснуi iдиний оператор тАУ ![]() Ватакий, що
Ватакий, що ![]() .
.
РЖз перелiчених властивостей лiнiйних операцiй над елементами множини![]()
![]() Вавипливаi, що множина
Вавипливаi, що множина ![]() Вапо вiдношенню до операцii суми операторiв i адитивною абелевою групою. Операцiя множення на число маi такi властивостi
Вапо вiдношенню до операцii суми операторiв i адитивною абелевою групою. Операцiя множення на число маi такi властивостi ![]()
![]() .
.
Всi перелiченi властивостi лiнiйних операцiй над елементами множини ![]() Вадозволяi стверджувати, що множина
Вадозволяi стверджувати, що множина ![]() Ваi лiнiйним простором над полем комплексних чисел. Звiдси випливаi, що можна ставити питання про розмiрнiсть цього простору, про його базиси, пiдпросторiв.
Ваi лiнiйним простором над полем комплексних чисел. Звiдси випливаi, що можна ставити питання про розмiрнiсть цього простору, про його базиси, пiдпросторiв.
2. Лiнiйнi перетворення (оператори) iз простору V в V
В подальшому будемо розглядати лiнiйнi оператори, дiючi iз лiнiйного простору ![]() Вав той самий простiр. Цi оператори називають також перетвореннями iз
Вав той самий простiр. Цi оператори називають також перетвореннями iз ![]() Вав
Вав ![]() .
.
Назвемо тотожнiм (одиничним) оператор ![]() Ватакий, що для любого вектора
Ватакий, що для любого вектора ![]() Вапростору
Вапростору ![]() . Очевидно,
. Очевидно, ![]() ,
, ![]() , для любих
, для любих ![]() . З цього випливаi, оператор
. З цього випливаi, оператор ![]() ВатАУ лiнiйний i, тому,
ВатАУ лiнiйний i, тому, ![]() . Неважко упевнитися в тому, що оператор
. Неважко упевнитися в тому, що оператор ![]() ВатАУ iдиний. Дiйсно, якщо припустити що, крiм тотожного оператора
ВатАУ iдиний. Дiйсно, якщо припустити що, крiм тотожного оператора ![]() Ваз
Ваз ![]() , iснуi ще один тотожний оператор
, iснуi ще один тотожний оператор ![]() , тодi для будь-якого
, тодi для будь-якого ![]() Вабудемо мати
Вабудемо мати ![]() ,
, ![]() , очевидно,
, очевидно, ![]() , тобто
, тобто ![]() .
.
Введемо операцiю множення операторiв. Нехай ![]() Вата
Вата ![]() ВатАУ два будь-яких лiнiйних оператора з
ВатАУ два будь-яких лiнiйних оператора з ![]() , а
, а ![]() ВатАУ довiльний вектор простору
ВатАУ довiльний вектор простору ![]() . Очевидно вектор
. Очевидно вектор ![]() , тому цей вектор можна привести за допомогою оператора
, тому цей вектор можна привести за допомогою оператора ![]() . В результатi вектор
. В результатi вектор ![]() Вабуде перетворений до вектору
Вабуде перетворений до вектору ![]() . Оператор, який приводить довiльний вектор
. Оператор, який приводить довiльний вектор ![]() Вапростору
Вапростору ![]() Вау вектор
Вау вектор ![]() , називаiться добутком операторiв
, називаiться добутком операторiв ![]() Вата
Вата ![]() Ваi позначаiться так:
Ваi позначаiться так: ![]() . За означенням добутку операторiв
. За означенням добутку операторiв ![]() Ваi
Ваi ![]()
![]() Вадля будь-якого вектору
Вадля будь-якого вектору ![]() . Легко перевiрити, що
. Легко перевiрити, що ![]()
![]() ,
, ![]() , де
, де ![]() ВатАУ довiльно вибране комплексне число. З цього слiдуi, що добуток лiнiйних операторiв i лiнiйним оператором, тобто
ВатАУ довiльно вибране комплексне число. З цього слiдуi, що добуток лiнiйних операторiв i лiнiйним оператором, тобто ![]() . Зауважимо, що
. Зауважимо, що ![]() .
.
Операцii додавання та множення лiнiйних операторiв мають наступнi властивостi
1) ![]() , 3)
, 3) ![]() ,
,
2) ![]() , 4)
, 4) ![]() .
.
Для iлюстрацii способу доведення цих властивостей доведемо властивiсть ![]() . Нехай
. Нехай ![]() ВатАУ довiльний вектор простору
ВатАУ довiльний вектор простору ![]() . Для довiльного вектору
. Для довiльного вектору ![]() Вапростору
Вапростору ![]() за означенням добутку i суми операторiв маi
за означенням добутку i суми операторiв маi

Таким чином, ![]() , тобто
, тобто ![]() .
.
Якщо для оператору ![]() Ваможна вказати такий лiнiйний оператор
Ваможна вказати такий лiнiйний оператор ![]() , що
, що ![]() , то оператор
, то оператор ![]() Ваназивають оберненим для оператору
Ваназивають оберненим для оператору ![]() . Можна показати, що оператор
. Можна показати, що оператор ![]() ВатАУ iдиний.
ВатАУ iдиний.
Покажемо, що оператор ![]() , що маi обернений, перетворюi ненульовий вектор в ненульовий, тобто якщо
, що маi обернений, перетворюi ненульовий вектор в ненульовий, тобто якщо ![]() , то й
, то й ![]() . Спочатку доведемо, що
. Спочатку доведемо, що ![]() . Дiйсно, так як
. Дiйсно, так як ![]() ВатАУ лiнiйний оператор, то для будь-якого
ВатАУ лiнiйний оператор, то для будь-якого ![]()
![]() . Доведене твердження справедливе для будь-якого лiнiйного оператора, в тому числi i для оператора, що маi обернений, i для оператора
. Доведене твердження справедливе для будь-якого лiнiйного оператора, в тому числi i для оператора, що маi обернений, i для оператора ![]() . Нехай
. Нехай ![]() Ваi
Ваi ![]() . Так як оператор
. Так як оператор ![]() Вамаi обернений, то
Вамаi обернений, то ![]() , тобто
, тобто ![]() . Якщо припустити, що деякому
. Якщо припустити, що деякому ![]() Вавiдповiдаi вектор
Вавiдповiдаi вектор ![]() , тодi на основi установлених рiвностей
, тодi на основi установлених рiвностей ![]() Ваi
Ваi ![]() виходило б, що
виходило б, що ![]() . А це заперечуi початковому фактовi, що
. А це заперечуi початковому фактовi, що ![]() . З цього випливаi, що припущення про те, що для деякого
. З цього випливаi, що припущення про те, що для деякого ![]()
![]() , невiрно, тому для будь тАУ якого
, невiрно, тому для будь тАУ якого ![]()
![]() .
.
Доведемо ще одну властивiсть оператора ![]() , що маi обернений. Такий оператор два рiзних вектора
, що маi обернений. Такий оператор два рiзних вектора ![]() Вата
Вата ![]() Ваперетворюi у два рiзнi вектори
Ваперетворюi у два рiзнi вектори ![]() Ваi
Ваi ![]() . Дiйсно, якщо припустити противне, що iснують такi нерiвнi один одному
. Дiйсно, якщо припустити противне, що iснують такi нерiвнi один одному ![]() Ваi
Ваi ![]() , для яких
, для яких ![]() , тодi для таких
, тодi для таких ![]() Ваi
Ваi ![]()
![]() Ваабо, що те саме
Ваабо, що те саме ![]() . За умовою оператор
. За умовою оператор ![]() Вамаi обернений. За доведеною вище властивiстю такого оператора iз рiвностi
Вамаi обернений. За доведеною вище властивiстю такого оператора iз рiвностi ![]() Вавипливаi, що
Вавипливаi, що ![]() , тобто
, тобто ![]() . Ми прийшли до протирiччя з тим фактом, що за умовою
. Ми прийшли до протирiччя з тим фактом, що за умовою ![]() . З цього випливаi, що будь тАУ яким двом рiзним векторам
. З цього випливаi, що будь тАУ яким двом рiзним векторам ![]() Ваi
Ваi ![]() Вавiдповiдають рiзнi образи
Вавiдповiдають рiзнi образи ![]() Ваi
Ваi ![]() .
.
Оператор ![]() Ваназивають взаiмно тАУ однозначним, якщо два будь тАУ якi рiзнi вектори
Ваназивають взаiмно тАУ однозначним, якщо два будь тАУ якi рiзнi вектори ![]() Ваi
Ваi ![]() Вавiн перетворюi у рiзнi вектори
Вавiн перетворюi у рiзнi вектори ![]() Ваi
Ваi ![]() . РЖз наведеного вище випливаi, що оператор
. РЖз наведеного вище випливаi, що оператор ![]() , що маi обернений, i взаiмно тАУ однозначним. Для взаiмно тАУ однозначного оператора неважко довести таку властивiсть: якщо
, що маi обернений, i взаiмно тАУ однозначним. Для взаiмно тАУ однозначного оператора неважко довести таку властивiсть: якщо ![]() , то i
, то i ![]() . Покажемо, що взаiмно тАУ однозначний оператор
. Покажемо, що взаiмно тАУ однозначний оператор ![]() Валiнiйно незалежнi вектори
Валiнiйно незалежнi вектори ![]() ,
, ![]() , тАж,
, тАж, ![]() Ваперетворюi в лiнiйно незалежнi вектори
Ваперетворюi в лiнiйно незалежнi вектори ![]() ,
, ![]() , тАж,
, тАж, ![]() . Для доведення цього твердження скористаiмося методом Влвiд противногоВ». Припустимо противне, що вектори
. Для доведення цього твердження скористаiмося методом Влвiд противногоВ». Припустимо противне, що вектори ![]() , тАж,
, тАж, ![]() ВатАУ лiнiйно незалежнi. Тодi можна знайти такi не рiвню нулю числа,
ВатАУ лiнiйно незалежнi. Тодi можна знайти такi не рiвню нулю числа, ![]() Ващо
Ващо ![]() . Так як оператор
. Так як оператор ![]() ВатАУ лiнiйний, то
ВатАУ лiнiйний, то ![]() .
.
Звiдси за властивiстю взаiмно-однозначного оператора ![]() , тобто вектори
, тобто вектори ![]() ,
, ![]() , тАж,
, тАж, ![]() Вавиявляються лiнiйно залежними. Протирiччя з умовою ствердження означаi, що вектори
Вавиявляються лiнiйно залежними. Протирiччя з умовою ствердження означаi, що вектори ![]() ,
, ![]() , тАж,
, тАж, ![]() Валiнiйно незалежнi.
Валiнiйно незалежнi.
РЖз доведеного випливаi, що будь-який вектор ![]() Вапростору
Вапростору ![]() Вамаi iдиний прообраз
Вамаi iдиний прообраз ![]() Ватакий, що
Ватакий, що ![]() . Доведемо тiльки iднiсть прообразу вектора
. Доведемо тiльки iднiсть прообразу вектора ![]() . Дiйсно, якщо припустити, що вектор
. Дiйсно, якщо припустити, що вектор ![]() Вамаi декiлька рiзноманiтних прообразiв, наприклад,
Вамаi декiлька рiзноманiтних прообразiв, наприклад, ![]() Ваi
Ваi ![]() , то виявиться, що
, то виявиться, що ![]() . Звiдси
. Звiдси ![]() , маiмо
, маiмо ![]() , так як оператор взаiмно-однозначний. Отже, якщо оператор
, так як оператор взаiмно-однозначний. Отже, якщо оператор ![]() ВатАУ взаiмно-однозначний, то кожному вектору
ВатАУ взаiмно-однозначний, то кожному вектору ![]() Вапростору
Вапростору ![]() Вавiн ставить у вiдповiднiсть один i тiльки один вектор
Вавiн ставить у вiдповiднiсть один i тiльки один вектор ![]() . Звiдси випливаi, що взаiмно-однозначний оператор маi обернений.
. Звiдси випливаi, що взаiмно-однозначний оператор маi обернений.
Пiдводячи пiдсумок сказаному вище про властивостi оберненого i взаiмно-однозначного операторiв, сформулюiмо наступне твердження.
Теорема 2.1. Для того, щоб лiнiйний оператор ![]() Вамав обернений необхiдно i достатньо, щоб вiн був взаiмно-однозначним.
Вамав обернений необхiдно i достатньо, щоб вiн був взаiмно-однозначним.
Введемо поняття ядра й образу оператора. Ядром лiнiйного оператора ![]() Ваназивають таку множину
Ваназивають таку множину ![]() Вавекторiв простору
Вавекторiв простору ![]() , що для любого
, що для любого ![]()
![]() . Вiдомо, що будь-який лiнiйний оператор приводить вектор
. Вiдомо, що будь-який лiнiйний оператор приводить вектор ![]() Вав
Вав ![]() , тобто
, тобто ![]() , тому ядро довiльного лiнiйного оператора не i пустою множиною, так як воно завжди мiстить оператор
, тому ядро довiльного лiнiйного оператора не i пустою множиною, так як воно завжди мiстить оператор ![]() .
.
Теорема 2.2. Якщо ![]() Вамiстить iдиний вектор
Вамiстить iдиний вектор ![]() , то оператор
, то оператор ![]() Ваi взаiмно-однозначним.
Ваi взаiмно-однозначним.
Доведення. Нехай ![]() - два довiльно взятих вектора лiнiйного простору. Якщо показати, що
- два довiльно взятих вектора лiнiйного простору. Якщо показати, що ![]() , то це буде означати, що оператор
, то це буде означати, що оператор ![]() Ваi взаiмно-однозначним. Припустимо противне, що знайдуться два вектора
Ваi взаiмно-однозначним. Припустимо противне, що знайдуться два вектора ![]() Ваi
Ваi ![]() , такi, що
, такi, що ![]() , а
, а ![]() . Тодi для цих векторiв
. Тодi для цих векторiв ![]() . За умовою теореми
. За умовою теореми ![]() Васкладаiться iз iдиного вектора
Васкладаiться iз iдиного вектора ![]() , тобто для вектора
, тобто для вектора ![]() Ваi тiльки для нього
Ваi тiльки для нього ![]() . В силу цього
. В силу цього ![]() Вачи
Вачи ![]() . Ми прийшли до протирiччя з припущенням про те, що
. Ми прийшли до протирiччя з припущенням про те, що ![]() . Тому для будь-яких не рiвних один одному векторiв
. Тому для будь-яких не рiвних один одному векторiв ![]() Ваi
Ваi ![]() Вапростору
Вапростору ![]()
![]() . Отже, твердження теореми вiрне.
. Отже, твердження теореми вiрне.
Теорема 2.3. Для того, щоб оператор ![]() Вамав обернений, необхiдно i достатньо, щоб
Вамав обернений, необхiдно i достатньо, щоб ![]() .
.
Доведення цiii теореми основуiться на теоремах 2.1 i 2.2 про обернений оператор i ядро взаiмно-однозначного оператора.
Образом оператора ![]() Ваназиваiться множина
Ваназиваiться множина ![]() всiх векторiв простору
всiх векторiв простору ![]() , кожний з яких маi прообраз, тобто якщо
, кожний з яких маi прообраз, тобто якщо ![]() , то iснуi такий вектор
, то iснуi такий вектор ![]() , що
, що ![]() . Легко побачити, що якщо
. Легко побачити, що якщо ![]() Вамiстить тiльки нульовий вектор, то
Вамiстить тiльки нульовий вектор, то ![]() Ваi весь лiнiйний простiр
Ваi весь лiнiйний простiр ![]() :
: ![]() . Дiйсно, якщо
. Дiйсно, якщо ![]() , то оператор
, то оператор ![]() Ваi взаiмно-однозначним. За доведеною вище властивiстю взаiмно-однозначного оператора кожний вектор
Ваi взаiмно-однозначним. За доведеною вище властивiстю взаiмно-однозначного оператора кожний вектор ![]() Вапростору
Вапростору ![]() Вамаi iдиний прообраз
Вамаi iдиний прообраз ![]() :
: ![]() , так що
, так що ![]() .
.
Покажемо тепер, що множина ![]() Вадля довiльного лiнiйного простору
Вадля довiльного лiнiйного простору ![]() Ваi пiдпростором лiнiйного простору
Ваi пiдпростором лiнiйного простору ![]() . Нехай
. Нехай ![]() Ваi
Ваi ![]() ВатАУ два довiльно взятих вектори множини
ВатАУ два довiльно взятих вектори множини ![]() . Так як
. Так як ![]() , то
, то ![]() . Нехай
. Нехай ![]() ВатАУ довiльне число. Так як
ВатАУ довiльне число. Так як ![]() , то
, то ![]() . Таким чином, лiнiйнi операцii над будь-якими векторами множини
. Таким чином, лiнiйнi операцii над будь-якими векторами множини ![]() Вадають вектори тiii ж множини, тобто
Вадають вектори тiii ж множини, тобто ![]() ВатАУ пiдпростiр простору
ВатАУ пiдпростiр простору ![]() .
.
Аналогiчним способом доводиться, що множина ![]() Ватакож i пiдпростором простору
Ватакож i пiдпростором простору ![]() .
.
Розмiрнiсть пiдпростору ![]() Ваназиваiться дефектом оператора
Ваназиваiться дефектом оператора![]() . Розмiрнiсть пiдпростору
. Розмiрнiсть пiдпростору ![]() Ваназиваiться рангом оператора
Ваназиваiться рангом оператора ![]() . Для рангу оператора
. Для рангу оператора ![]() Вавикористовуiться одне з позначень
Вавикористовуiться одне з позначень ![]() Ваабо
Ваабо ![]() , для позначення дефекту оператора використовуiться символ
, для позначення дефекту оператора використовуiться символ ![]() .
.
Теорема 2.4. Для будь-якого лiнiйного оператора ![]() Ваiз
Ваiз ![]() сума розмiнностей його ядра i образу дорiвнюi розмiрностi простору
сума розмiнностей його ядра i образу дорiвнюi розмiрностi простору ![]() , тобто
, тобто ![]() або
або ![]() .
.
Теорема 2.5. Нехай ![]() Ваi
Ваi ![]() - два яких-небудь пiдпростори
- два яких-небудь пiдпростори ![]() - мiрного простору
- мiрного простору ![]() , причому
, причому ![]() . Тодi iснуi такий лiнiйний оператор
. Тодi iснуi такий лiнiйний оператор ![]() , що
, що ![]() , а
, а ![]() .
.
Доведення. Нехай ![]() - розмiрнiсть пiдпростору
- розмiрнiсть пiдпростору ![]() , тобто
, тобто ![]() , а
, а ![]() ВатАУ розмiрнiсть пiдпростору
ВатАУ розмiрнiсть пiдпростору ![]() . За умовою теореми
. За умовою теореми ![]() . Виберемо базис
. Виберемо базис ![]()
![]() - мiрного простору
- мiрного простору ![]() Ватак, щоб
Ватак, щоб ![]() Вавекторiв
Вавекторiв ![]() Вабуло базисом пiдпростору
Вабуло базисом пiдпростору ![]() . В пiдпросторi
. В пiдпросторi ![]() Вавiзьмемо який-небудь базис
Вавiзьмемо який-небудь базис ![]() . Розглянемо лiнiйний оператор
. Розглянемо лiнiйний оператор ![]() , який перетворюi вектори
, який перетворюi вектори ![]() простору
простору ![]() Вау вектори
Вау вектори ![]() , а кожний з векторiв
, а кожний з векторiв ![]() у нульовий вектор, тобто
у нульовий вектор, тобто ![]() .
.
Оператор ![]() Вадовiльний вектор
Вадовiльний вектор ![]() Вапростору
Вапростору ![]() Ваприводить у вектор
Ваприводить у вектор ![]()
![]() , який належить пiдпростору
, який належить пiдпростору ![]() Вапростора
Вапростора ![]() . Звiдси випливаi, що
. Звiдси випливаi, що ![]() , тобто пiдпростiр
, тобто пiдпростiр ![]() Вамiстить образ оператора
Вамiстить образ оператора ![]() . Щоб довести, що
. Щоб довести, що ![]() , треба за означенням множини
, треба за означенням множини ![]() Вапоказати, що будь-який вектор
Вапоказати, що будь-який вектор ![]() Вапiдпростору
Вапiдпростору ![]() , маi прообраз у просторi
, маi прообраз у просторi ![]() . Розглянутий лiнiйний оператор
. Розглянутий лiнiйний оператор ![]() Ваперетворюi вектори
Ваперетворюi вектори ![]() Вапростору
Вапростору ![]() Вау вектори
Вау вектори ![]() , тому довiльно взятий вектор
, тому довiльно взятий вектор ![]() Вапiдпростору
Вапiдпростору ![]() Ваможна представити у виглядi
Ваможна представити у виглядi ![]() . В силу лiнiйностi оператора и також того, що
. В силу лiнiйностi оператора и також того, що ![]() , вектор
, вектор ![]() Ваможна представити також i в такiй формi:
Ваможна представити також i в такiй формi: ![]()
![]() , де
, де ![]() ВатАУ довiльно вибранi комплекснi числа. Останнiй вираз для довiльного вектору
ВатАУ довiльно вибранi комплекснi числа. Останнiй вираз для довiльного вектору ![]() Ваозначаi, що вiн i образом вектора
Ваозначаi, що вiн i образом вектора ![]() Вапростору
Вапростору ![]() . Таким чином,
. Таким чином, ![]() .
.
Покажемо тепер, що пiдпростiр ![]() Ваi ядром оператора
Ваi ядром оператора ![]() . Нехай
. Нехай ![]() Ваякий-небудь вектор пiдпростору
Ваякий-небудь вектор пiдпростору ![]() . Так як
. Так як ![]() , то це означаi, що вектор
, то це означаi, що вектор ![]() Вавходить в ядро оператора
Вавходить в ядро оператора ![]() . Звiдси випливаi, що пiдпростiр
. Звiдси випливаi, що пiдпростiр ![]() . Для доведення того, що
. Для доведення того, що ![]() треба показати, що будь-який вектор
треба показати, що будь-який вектор ![]() Вапростору
Вапростору ![]() , що не належить пiдпростору
, що не належить пiдпростору ![]() , не може бути елементом ядра оператора
, не може бути елементом ядра оператора ![]() . Нехай
. Нехай ![]() - вектор простору
- вектор простору ![]() , який не належить пiдпростору
, який не належить пiдпростору ![]() . Зрозумiло, що хоча б одна iз координат
. Зрозумiло, що хоча б одна iз координат ![]() Вацього вектору не рiвна нулю, так як в протилежному випадку
Вацього вектору не рiвна нулю, так як в протилежному випадку ![]() . Розглянемо
. Розглянемо ![]() . Так як
. Так як ![]() Валiнiйно незалежнi вектори, а серед чисел
Валiнiйно незалежнi вектори, а серед чисел ![]() Ваi вiдмiннi вiд нуля, то
Ваi вiдмiннi вiд нуля, то ![]() . Це означаi, що будь-який вектор, що не належить пiдпростору
. Це означаi, що будь-який вектор, що не належить пiдпростору ![]() , не належить i ядру оператора
, не належить i ядру оператора ![]() . Отже,
. Отже, ![]() .
.
Теорема 2.6. Нехай ![]() Ваi
Ваi ![]() ВатАУ два яких-небудь лiнiйних оператора iз множини
ВатАУ два яких-небудь лiнiйних оператора iз множини ![]() , тодi
, тодi ![]() ,
, ![]() .
.
Доведення. Нехай ![]() ВатАУ довiльний вектор простору
ВатАУ довiльний вектор простору ![]() . Зрозумiло, що
. Зрозумiло, що ![]() . Будь-який вектор
. Будь-який вектор ![]() Вамножини
Вамножини ![]() Ваза означенням добутку операторiв це вектор
Ваза означенням добутку операторiв це вектор ![]() . Останнiй i вектором множини
. Останнiй i вектором множини ![]() . З цього слiдуi, що маi мiсце включення
. З цього слiдуi, що маi мiсце включення ![]() . А це означаi, що
. А це означаi, що ![]() , тобто
, тобто ![]() . Перше твердження теореми доведено.
. Перше твердження теореми доведено.
Доведемо справедливiсть другого. Нехай ![]() ВатАУ довiльний вектор ядра оператора
ВатАУ довiльний вектор ядра оператора ![]() , тодi
, тодi ![]() , i, тому,
, i, тому, ![]() . Це означаi, що якщо
. Це означаi, що якщо ![]() , то
, то ![]() , тобто
, тобто ![]() . Звiдси випливаi нерiвнiсть
. Звiдси випливаi нерiвнiсть ![]() . Позначимо через
. Позначимо через ![]() Варозмiрнiсть простору
Варозмiрнiсть простору ![]() . Згiдно теореми 2.4
. Згiдно теореми 2.4 ![]() ,
, ![]() . Так як
. Так як ![]() , то
, то ![]() , тобто
, тобто ![]() .
.
Теорема 2.7. Нехай ![]() ВатАУ розмiрнiсть простору
ВатАУ розмiрнiсть простору ![]() ,
, ![]() Ваi
Ваi ![]() ВатАУ лiнiйнi оператори iз
ВатАУ лiнiйнi оператори iз ![]() , тодi
, тодi ![]() .
.
3. Матриця лiнiйного оператора
Нехай ![]() - деякий базис лiнiйного простору
- деякий базис лiнiйного простору ![]() , а
, а ![]() ВатАУ який-небудь лiнiйний оператор, дiючий iз
ВатАУ який-небудь лiнiйний оператор, дiючий iз ![]() Вав
Вав ![]() . Вектор
. Вектор ![]() Ваоператор
Ваоператор ![]() Ваперетворюi в вектор
Ваперетворюi в вектор ![]() . Вектори
. Вектори ![]() Вапростору
Вапростору ![]() Варозкладемо по векторах базису
Варозкладемо по векторах базису ![]() Вацього простору. Побудуiмо матрицю
Вацього простору. Побудуiмо матрицю ![]() Вапорядку
Вапорядку ![]() , стовпцi якоi складенi iз координат векторiв
, стовпцi якоi складенi iз координат векторiв ![]() ,
,
 ,
, ![]() ,
, ![]() .
.
Матриця ![]() Ваназиваiться матрицею оператора
Ваназиваiться матрицею оператора ![]() Вав базисi
Вав базисi ![]() .
.
Приклад. Записати матрицю тотожного i нульового операторiв у базисi ![]() Вапростору
Вапростору ![]() .
.
РозвтАЩязок. Тотожний оператор ![]() Вабудь-який вектор простору
Вабудь-який вектор простору ![]() Ваприводить в той же самий оператор. Тому
Ваприводить в той же самий оператор. Тому ![]() . А це означаi, що матриця
. А це означаi, що матриця ![]() Ватотожного оператора буде одиничною в будь-якому базисi простору
Ватотожного оператора буде одиничною в будь-якому базисi простору ![]() . Нульовий оператор
. Нульовий оператор ![]() Вабудь-який вектор простору
Вабудь-який вектор простору ![]() Ваперетворюi в нульовий вектор, тому матриця
Ваперетворюi в нульовий вектор, тому матриця ![]() Вацього оператора тАУ нульова в будь-якому базисi.
Вацього оператора тАУ нульова в будь-якому базисi.
РЖз сказаного вище випливаi, що в обраному базисi ![]() -мiрного простору
-мiрного простору ![]() Ваз кожним лiнiйним оператором
Ваз кожним лiнiйним оператором ![]() Ваможна звтАЩязати квадратну матрицю
Ваможна звтАЩязати квадратну матрицю ![]() Вапорядку
Вапорядку ![]() . Виникаi питання: чи можна кожнiй квадратнiй матрицi
. Виникаi питання: чи можна кожнiй квадратнiй матрицi ![]() Вапорядку
Вапорядку ![]() Вапоставити у вiдповiднiсть такий лiнiйний оператор
Вапоставити у вiдповiднiсть такий лiнiйний оператор ![]() , матриця якого в заданому базисi
, матриця якого в заданому базисi ![]() Вапростору
Вапростору ![]() Васпiвпадаi з матрицею
Васпiвпадаi з матрицею ![]() ? Стверджувальну вiдповiдь на це питання даi
? Стверджувальну вiдповiдь на це питання даi
Теорема 3.1. Нехай ![]() ВатАУ деяка квадратна матриця порядку
ВатАУ деяка квадратна матриця порядку ![]() . Нехай
. Нехай ![]() ВатАУ довiльний обраний базис
ВатАУ довiльний обраний базис ![]() -мiрного лiнiйного простору
-мiрного лiнiйного простору ![]() . Тодi iснуi iдиний лiнiйний оператор
. Тодi iснуi iдиний лiнiйний оператор ![]() , який у вказаному базисi маi матрицю
, який у вказаному базисi маi матрицю ![]() .
.
Доведення. Розглянемо лiнiйний оператор ![]() , який вектори
, який вектори ![]() Вабазису простору
Вабазису простору ![]() Ваперетворюi у вектори
Ваперетворюi у вектори ![]() ,
, ![]() . У базисi
. У базисi ![]() Ваоператор
Ваоператор ![]() , очевидно, маi матрицю
, очевидно, маi матрицю ![]() . Залишаiться довести, що i iдиним оператором з матрицею. Припустимо протилежне, що, крiм оператора
. Залишаiться довести, що i iдиним оператором з матрицею. Припустимо протилежне, що, крiм оператора ![]() , iснуi ще лiнiйний оператор
, iснуi ще лiнiйний оператор ![]() , маючий матрицю
, маючий матрицю ![]() Вав базисi
Вав базисi ![]() . Це означаi, що
. Це означаi, що ![]() ,
, ![]() . Виберемо який-небудь вектор
. Виберемо який-небудь вектор ![]() Вапростору
Вапростору ![]() Ваi розглянемо вектори
Ваi розглянемо вектори ![]() Ваi
Ваi ![]() . Маiмо
. Маiмо ![]()
![]() .
.
Як наслiдок, що для будь-якого ![]()
![]() . Звiдси витiкаi, що
. Звiдси витiкаi, що ![]() . Теорему доведено.
. Теорему доведено.
Теорема 3.2. Нехай ![]() ВатАУ матриця лiнiйного оператора
ВатАУ матриця лiнiйного оператора ![]() Вав базисi
Вав базисi ![]() Вапростору
Вапростору ![]() . Ранг оператора
. Ранг оператора ![]() Вадорiвнюi рангу його матрицi:
Вадорiвнюi рангу його матрицi: ![]() .
.
Доведення. В основi доведення лежать означення рангу оператора i рангу матрицi: ![]() , ранг матрицi
, ранг матрицi ![]() Вадорiвнюi рангу системи його стовпцiв.
Вадорiвнюi рангу системи його стовпцiв.
Нехай ![]() ВатАУ який-небудь вектор
ВатАУ який-небудь вектор ![]() - мiрного простору
- мiрного простору ![]() . Образом вектора
. Образом вектора ![]() Ваi вектор
Ваi вектор ![]()
![]() . Як бачимо, довiльний вектор образу оператора
. Як бачимо, довiльний вектор образу оператора ![]() , тобто множини
, тобто множини ![]() , представляi собою лiнiйну комбiнацiю векторiв
, представляi собою лiнiйну комбiнацiю векторiв ![]() . Отже,
. Отже, ![]() Ваi лiнiйною оболонкою множини векторiв
Ваi лiнiйною оболонкою множини векторiв ![]() . Вiдомо, що розмiрнiсть лiнiйноi оболонки дорiвнюi ранговi системи векторiв, якi вони утворюють, тому
. Вiдомо, що розмiрнiсть лiнiйноi оболонки дорiвнюi ранговi системи векторiв, якi вони утворюють, тому ![]() . За означенням у стовпцях матрицi
. За означенням у стовпцях матрицi ![]() Ваоператора
Ваоператора ![]() Варозмiщенi координати векторiв
Варозмiщенi координати векторiв ![]() Вау базисi
Вау базисi ![]() . Отже, на основi означення рангу матрицi
. Отже, на основi означення рангу матрицi ![]() . Таким чином,
. Таким чином, ![]() .
.
Нехай ![]() Ваi
Ваi ![]() Ваматрицi операторiв
Ваматрицi операторiв ![]() Ваi
Ваi ![]() Вав якому-небудь базисi простору
Вав якому-небудь базисi простору ![]() , тодi iз способу побудови цих матриць витiкаi, що матрицi операторiв
, тодi iз способу побудови цих матриць витiкаi, що матрицi операторiв ![]() Ваi
Ваi ![]() , де
, де ![]() Ваi
Ваi ![]() ВатАУ довiльно взятi числа, рiвнi вiдповiдно
ВатАУ довiльно взятi числа, рiвнi вiдповiдно ![]() Ваi
Ваi ![]() . Доведемо справедливiсть першого твердження, як бiльш складного. Дiйсно, стовпцi матрицi оператора
. Доведемо справедливiсть першого твердження, як бiльш складного. Дiйсно, стовпцi матрицi оператора ![]() Вапобудованi iз координат векторiв
Вапобудованi iз координат векторiв ![]() Вау базисi
Вау базисi ![]() Вапростору
Вапростору ![]() . Визначимо елементи
. Визначимо елементи ![]() -го стовпця цiii матрицi, тобто координати вектора
-го стовпця цiii матрицi, тобто координати вектора ![]() . Маiмо
. Маiмо

Звiдси видно, що довiльний елемент ![]() Ваматрицi
Ваматрицi ![]() Ваоператора
Ваоператора ![]() дорiвнюi
дорiвнюi ![]() , тобто дорiвнюi сумi добуткiв елементiв
, тобто дорiвнюi сумi добуткiв елементiв ![]() -го рядка матрицi
-го рядка матрицi ![]() Вана вiдповiдний елемент
Вана вiдповiдний елемент ![]() -го стовпця матрицi
-го стовпця матрицi ![]() . А це означаi, що
. А це означаi, що ![]() . Твердження доведено.
. Твердження доведено.
РЖз доведеного твердження i теорем 2.6, 2.7 про ранг оператора ![]() Васлiдуi справедливiсть таких нерiвностей для двох добуткiв квадратних матриць
Васлiдуi справедливiсть таких нерiвностей для двох добуткiв квадратних матриць ![]() Ваi
Ваi ![]() Ваодного порядку
Ваодного порядку ![]() .
.
![]() ,
, ![]() ,
,
![]()
Вiдомо, що необхiдною i достатньою умовою iснування оберненого оператора для оператора ![]() , i умова
, i умова ![]() , де
, де ![]() ВатАУ розмiрнiсть простору
ВатАУ розмiрнiсть простору ![]() . РЖз теореми 3.2 витiкаi, що остання умова еквiвалентна вимозi: матриця
. РЖз теореми 3.2 витiкаi, що остання умова еквiвалентна вимозi: матриця ![]() Ваоператора
Ваоператора ![]() Ваповинна бути не виродженою.
Ваповинна бути не виродженою.
РЖншими словами, щоб оператор ![]() Вамав обернений необхiдно i достатньо, щоб його матриця в якому-небудь базисi лiнiйного простору
Вамав обернений необхiдно i достатньо, щоб його матриця в якому-небудь базисi лiнiйного простору ![]() Вавиявилась не виродженою.
Вавиявилась не виродженою.
4. Перетворення матрицi оператора при замiнi базису
Нехай у просторi ![]() Ваобранi два базиси
Ваобранi два базиси ![]() Ваi
Ваi ![]() . Перший базис для зручностi назвемо старим, а другий тАУ новим. Координати векторiв
. Перший базис для зручностi назвемо старим, а другий тАУ новим. Координати векторiв ![]() Вау старому базисi розмiстимо у стовпцях матрицi
Вау старому базисi розмiстимо у стовпцях матрицi
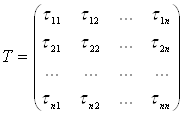 .
.
Побудована матриця називаiться матрицею переходу вiд старого базису до нового. Вектори ![]() Валiнiйно незалежнi, тому
Валiнiйно незалежнi, тому ![]() Ваi, звiсно, матриця
Ваi, звiсно, матриця ![]() Ване вироджена.
Ване вироджена.
Згiдно сказаному

![]() (4.1)
(4.1)
Цi формули звтАЩязку мiж векторами старого i нового базисiв у матричному записi мають вигляд
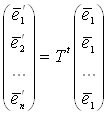 ,
,
де ![]() ВатАУ транспонована матриця
ВатАУ транспонована матриця ![]() .
.
Теорема 4.1. Матрицi ![]() Ваi
Ваi ![]() Ваоператора
Ваоператора ![]() Вав базисах
Вав базисах ![]() Ваi
Ваi ![]() ВазвтАЩязанi спiввiдношеннями
ВазвтАЩязанi спiввiдношеннями
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы