Дослiдження топологiчного визначення верхнiх напiвТСрат
Курсова робота: Дослiдження топологiчного визначення верхнiх напiвТСрат
Змiст
Роздiл 1
1. Упорядкованi множини
2. ТРрати
3. Дистрибутивнi ТСрати
4. Топологiчнi простори
Роздiл 2
1. Верхнi напiвТСрати
2. Стоуновий простiр
Висновок
Список лiтератури
Роздiл 1
1. Упорядкованi множини
Визначення: Упорядкованою множиною![]() Ваназиваiться непуста множина, на якоi визначене бiнарне вiдношення
Ваназиваiться непуста множина, на якоi визначене бiнарне вiдношення ![]() , що задовольняi для всiх
, що задовольняi для всiх ![]() Ванаступним умовам:
Ванаступним умовам:
1. Рефлективнiсть: ![]() .
.
2. Антисиметричнiсть: якщо ![]() Вай
Вай ![]() , те
, те ![]() .
.
3. Транзитивнiсть: якщо ![]() Вай
Вай ![]() , те
, те ![]() .
.
Якщо ![]() Вай
Вай ![]() , то говорять, що
, то говорять, що ![]() Ваменше
Ваменше ![]() Ваабо
Ваабо ![]() Вабiльше
Вабiльше ![]() , i пишуть
, i пишуть ![]() Ваабо
Ваабо ![]() .
.
Приклади впорядкованих множин:
Множина цiлих позитивних чисел, а ![]() Ваозначаi, що
Ваозначаi, що ![]() Вадiлить
Вадiлить ![]() .
.
Множина всiх дiйсних функцiй ![]() Вана вiдрiзку
Вана вiдрiзку ![]() Вай
Вай
![]() Ваозначаi, що
Ваозначаi, що ![]() Вадля
Вадля ![]() .
.
Визначення: Ланцюгом називаiтьсявпорядкована множина, на якоi для ![]() Вамаi мiсце
Вамаi мiсце ![]() Ваабо
Ваабо ![]() .
.
Використовуючи вiдношення порядку, можна одержати графiчне подання будь-якого кiнцевого впорядковання множини ![]() . Зобразимо кожний елемент множини
. Зобразимо кожний елемент множини ![]() Вау виглядi невеликого кружка, розташовуючи
Вау виглядi невеликого кружка, розташовуючи ![]() Вавище
Вавище ![]() , якщо
, якщо ![]() . З'iднаiмо
. З'iднаiмо ![]() Вай
Вай ![]() Вавiдрiзком. Отримана фiгура називаiться дiаграмою впорядкованоi множини
Вавiдрiзком. Отримана фiгура називаiться дiаграмою впорядкованоi множини ![]() .
.
Приклади дiаграм упорядкованих множин:
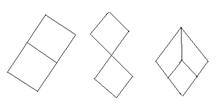
2. ТРрати
Визначення: Верхньою гранню пiдмножини ![]() Вав упорядкованiй множинi
Вав упорядкованiй множинi ![]() Ваназиваiться елемент
Ваназиваiться елемент ![]() Ваiз
Ваiз ![]() Ва, бiльший або рiвний усiх
Ва, бiльший або рiвний усiх ![]() Ваз
Ваз ![]() .
.
Визначення: Точна верхня грань пiдмножини ![]() Вавпорядкованоi множини
Вавпорядкованоi множини ![]() ВатАУ це така ii верхня грань, що менше будь-який iнший ii верхньоi гранi. Позначаiться символом
ВатАУ це така ii верхня грань, що менше будь-який iнший ii верхньоi гранi. Позначаiться символом ![]() Ваi читаiться Влсупремум XВ».
Ваi читаiться Влсупремум XВ».
Вiдповiдно до аксiоми антисиметричностi впорядкованоi множини, якщо точна верхня грань iснуi, то вона iдина.
Поняття нижньоi гранi й точноi гранi (яка позначаiться ![]() Вай читаiться ВлiнфинумВ»). Також, вiдповiдно до аксiоми антисиметричностi впорядкованоi множини, якщо точна нижня грань
Вай читаiться ВлiнфинумВ»). Також, вiдповiдно до аксiоми антисиметричностi впорядкованоi множини, якщо точна нижня грань ![]() Ваiснуi, то вона iдина.
Ваiснуi, то вона iдина.
Визначення: ТРратами![]() Ваназиваiться впорядкована множина
Ваназиваiться впорядкована множина ![]() , у якому будь-якi два елементи
, у якому будь-якi два елементи ![]() Вай
Вай ![]() Вамають точну нижню грань, позначувану
Вамають точну нижню грань, позначувану ![]() , i точну верхню грань, позначувану
, i точну верхню грань, позначувану ![]() .
.
Приклади ТСрат:
1. Будь-який ланцюг i ТСратами, тому що ![]() Вазбiгаiться з меншим, а
Вазбiгаiться з меншим, а ![]() Ваз бiльшим з елементiв
Ваз бiльшим з елементiв ![]() .
.
2.
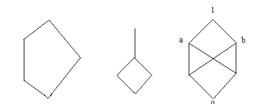
Найбiльший елемент, тобто елемент, бiльшого або рiвний кожного елемента впорядкованоi множини, позначають ![]() , а найменший елемент, тобто меншого або рiвний кожного елемента впорядкованоi множини, позначають
, а найменший елемент, тобто меншого або рiвний кожного елемента впорядкованоi множини, позначають ![]() .
.
На ТСратах можна розглядати двi бiнарнi операцii:
![]() Ва- додавання й
Ва- додавання й
![]() Ва- добуток
Ва- добуток
Цi операцii мають наступнi властивостi:
1. ![]() ,
, ![]() Ваiдемпотентнiсть
Ваiдемпотентнiсть
2. ![]() ,
, ![]() Вакомутативнiсть
Вакомутативнiсть
3. ![]() ,
,
![]() Ваасоцiативнiсть
Ваасоцiативнiсть
4. ![]() ,
,
![]() Вазакони поглинання
Вазакони поглинання
Теорема. Нехай ![]() Ва- множина iз двома бiнарними операцiями
Ва- множина iз двома бiнарними операцiями ![]() , що володiють властивостями (1) тАУ (4). Тодi вiдношення
, що володiють властивостями (1) тАУ (4). Тодi вiдношення ![]() Ва(або
Ва(або ![]() ) i порядком на
) i порядком на ![]() , а виникаюча впорядкована множина виявляiться ТСратами, причому:
, а виникаюча впорядкована множина виявляiться ТСратами, причому:
![]()
![]()
Доказ.
Рефлективнiсть вiдносини ![]() Вавипливаi iз властивостi (1). Помiтимо, що воно i наслiдком властивостi (4):
Вавипливаi iз властивостi (1). Помiтимо, що воно i наслiдком властивостi (4):
![]()
![]()
Якщо ![]() Вай
Вай ![]() , тобто
, тобто ![]() Вай
Вай ![]() , те в силу властивостi (2), одержимо
, те в силу властивостi (2), одержимо ![]() . Це означаi, що вiдношення
. Це означаi, що вiдношення ![]() Ваантисиметричне.
Ваантисиметричне.
Якщо ![]() Вай
Вай ![]() , то застосовуючи властивiсть (3), одержимо:
, то застосовуючи властивiсть (3), одержимо: ![]() , що доводить транзитивнiсть вiдносини
, що доводить транзитивнiсть вiдносини ![]() .
.
Застосовуючи властивостi (3), (1), (2), одержимо:
![]() ,
,
![]() .
.
Отже, ![]() Ваi
Ваi ![]()
Якщо ![]() Вай
Вай ![]() , то використовуючи властивостi (1) тАУ (3), маiмо:
, то використовуючи властивостi (1) тАУ (3), маiмо:
![]() , тобто
, тобто ![]()
По визначенню верхньоi гранi переконаiмося, що
![]()
РЖз властивостей (2), (4) випливаi, що ![]() Вай
Вай ![]()
Якщо ![]() Вай
Вай ![]() , то по властивостях (3), (4) одержимо:
, то по властивостях (3), (4) одержимо:
![]()
Звiдси по властивостях (2) i (4) треба, що
![]() , тобто
, тобто
Таким чином, ![]() . :
. :
Нехай ![]() ВаТСрати, тодi ii найбiльший елемент
ВаТСрати, тодi ii найбiльший елемент ![]() Вахарактеризуються одним iз властивостей:
Вахарактеризуються одним iз властивостей:
1.![]()
![]()
2.![]()
![]() .
.
Аналогiчно характеризуiться найменший елемент ![]() :
:
1.![]()
![]()
2.![]()
![]() .
.
3. Дистрибутивнi ТСрати
Визначення: ТРрати ![]() Ваназиваються дистрибутивноi, якщо для
Ваназиваються дистрибутивноi, якщо для ![]() виконуiться:
виконуiться:
1. ![]()
2. ![]()
У будь-яких ТСратах тотожностi (1) i (2) рiвносильнi. Доказ цього факту втримуiться в книзi [1], стор. 24.
Теорема: ТРрати ![]() Ваз 0 i 1 i дистрибутивною тодi й тiльки тодi, коли вона не мiстить у
Ваз 0 i 1 i дистрибутивною тодi й тiльки тодi, коли вона не мiстить у
Доказ цього факту можна знайти в книзi [2].
Далi пiд словом тАЬТСратитАЭ розумiiться довiльнi дистрибутивнi ТСрати з 0 i 1 (причому ![]() ).
).
Визначення: Непуста множина ![]() Ваназиваiться iдеалом у ТСратах
Ваназиваiться iдеалом у ТСратах ![]() , якщо виконуються умови:
, якщо виконуються умови:
1. ![]()
2. ![]()
Визначення: РЖдеал ![]() Вау ТСратах
Вау ТСратах ![]() Ваназиваiться простим, якщо
Ваназиваiться простим, якщо
![]() Ваабо
Ваабо ![]() .
.
РЖдеал, породжений множиною Н (тобтонайменший iдеал, що мiстить H), буде позначатися (Н]. Якщо Н = {a}, то замiсть ({a}] будемо писати (a] i називати (a] головним iдеалом.
Позначимо через I(L) множина всiх iдеалiв ТСрати L. I(L) будемо називати ТСратами iдеалiв.
Визначення: ТРрати ![]()
![]() Вай
Вай ![]()
![]() Ваназиваються iзоморфними (позначення:
Ваназиваються iзоморфними (позначення: ![]() ), якщо iснуi взаiмно однозначне вiдображення
), якщо iснуi взаiмно однозначне вiдображення ![]() , називане iзоморфiзмом, множини
, називане iзоморфiзмом, множини ![]() на множину
на множину ![]() , таке, що
, таке, що
![]() ,
,
![]() .
.
4. Топологiчнi простори
Визначення:Топологiчний простiр тАУ це непуста множина ![]() Ваз деякою системою
Ваз деякою системою ![]() Вавидiлених його пiдмножин, що задовольняi аксiомам:
Вавидiлених його пiдмножин, що задовольняi аксiомам:
Порожня множина й сам простiр ![]() Ваналежить системi
Ваналежить системi ![]() :
: ![]() .
.
Перетинання будь-якого кiнцевого числа множин з ![]() Ваналежить
Ваналежить ![]() , тобто
, тобто ![]() .
.
Об'iднання будь-якого сiмейства множин з ![]() Ваналежить
Ваналежить ![]() , тобто
, тобто ![]() .
.
Таким чином, топологiчний простiр тАУ це пари <![]() ,
, ![]() >, де
>, де ![]() Ва- така множина пiдмножин в
Ва- така множина пiдмножин в ![]() , що
, що ![]() Вай
Вай ![]() Вазамкнуто щодо кiнцевих перетинань i довiльних об'iднань. Множини з
Вазамкнуто щодо кiнцевих перетинань i довiльних об'iднань. Множини з ![]() Ваназивають вiдкритими, а iхнього доповнення в
Ваназивають вiдкритими, а iхнього доповнення в ![]() Вазамкнутими.
Вазамкнутими.
Визначення: Простiр називаiться компактним, якщо в будь-якому його вiдкритому покриттi можна вибрати кiнцеве пiдпокриття.
Визначення: Пiдмножина простору називаiться компактним, якщо в будь-якому його вiдкритому покриттi можна вибрати кiнцеве пiдпокриття.
Визначення: Топологiчний простiр називаiться ![]() Ва- простором, якщо для будь-яких двох рiзних його крапок iснуi вiдкрита множина, що мiстить рiвно одну iз цих крапок.
Ва- простором, якщо для будь-яких двох рiзних його крапок iснуi вiдкрита множина, що мiстить рiвно одну iз цих крапок.
Роздiл 2
1. Верхнi напiвТСрати
Визначення: множина називаiться верхнiми напiвТСратами, якщо sup{a,b} iснуi для будь-яких елементiв a i b.
Визначення: Непуста множина I верхнiх напiвТСрат L називаiться iдеалом, якщо для будь-яких ![]() Вавключення
Вавключення ![]() Вамаi мiсце тодi й тiльки тодi, коли
Вамаi мiсце тодi й тiльки тодi, коли ![]() .
.
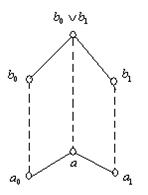
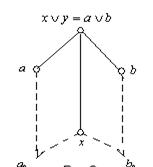
Визначення: Верхнi напiвТСрати ![]() Ваназиваються дистрибутивноi, якщо нерiвнiсть
Ваназиваються дистрибутивноi, якщо нерiвнiсть ![]() ≤
≤ ![]()
![]() Ва(
Ва(![]() ,
, ![]() ,
, ![]() ВаL) спричиняi iснування елементiв
ВаL) спричиняi iснування елементiв ![]() , таких, що
, таких, що ![]() ,
, ![]() , i
, i ![]() Ва=
Ва= ![]() .(мал.1). Помiтимо, що елементи
.(мал.1). Помiтимо, що елементи ![]() Вай
Вай ![]() Ване обов'язково iдинi.
Ване обов'язково iдинi.
Деякi найпростiшi властивостi дистрибутивних верхнiх напiвТСрат даi:
Лема 1:
(*). Якщо <![]() ,
,![]() > - довiльнi напiвТСрати, то верхнi напiвТСрати
> - довiльнi напiвТСрати, то верхнi напiвТСрати ![]() Вадистрибутивна тодi й тiльки тодi, коли ТСрати
Вадистрибутивна тодi й тiльки тодi, коли ТСрати ![]() Вадистрибутивна.
Вадистрибутивна.
(**). Якщо верхнi напiвТСрати ![]() Вадистрибутивна, то для будь-яких
Вадистрибутивна, то для будь-яких ![]() Ваiснуi елемент
Ваiснуi елемент ![]() , такий, що
, такий, що ![]() Вай
Вай ![]() . Отже, множина
. Отже, множина ![]() Ваi ТСратами.
Ваi ТСратами.
(***). Верхнi напiвТСрати ![]() Вадистрибутивна тодi й тiльки тодi, коли множина
Вадистрибутивна тодi й тiльки тодi, коли множина ![]() Ваi дистрибутивними ТСратами.
Ваi дистрибутивними ТСратами.
Доказ.
(*). ![]() Ва<
Ва<![]() ,
,![]() > - дистрибутивна й
> - дистрибутивна й ![]() , те для елементiв
, те для елементiв ![]() ,
, ![]() , справедлива рiвнiсть
, справедлива рiвнiсть ![]() :
:
![]()
виходить, напiвТСрати <![]() ,
,![]() > - дистрибутивна.
> - дистрибутивна.
![]()
![]() <
<![]() ,
,![]() > - дистрибутивна. Нехай ТСрати
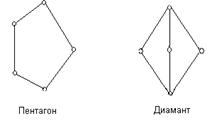
> - дистрибутивна. Нехай ТСрати ![]() Вамiстять дiамант або пентагон (мал.2).
Вамiстять дiамант або пентагон (мал.2).

1) Нехай ТСрати ![]() Вамiстять пентагон,
Вамiстять пентагон, ![]() . Потрiбно знайти такi елементи
. Потрiбно знайти такi елементи ![]() Вай
Вай ![]() , щоб виконувалася рiвнiсть
, щоб виконувалася рiвнiсть ![]() . Але множина елементiв менших або c складаiться з елементiв {0,b,c} i iхня нижня границя не дасть a. Одержали протирiччя з тим, що <
. Але множина елементiв менших або c складаiться з елементiв {0,b,c} i iхня нижня границя не дасть a. Одержали протирiччя з тим, що <![]() ,
,![]() > - дистрибутивна. Виходить, наше припущення невiрно й ТСрати
> - дистрибутивна. Виходить, наше припущення невiрно й ТСрати ![]() Ване мiстять пентагона.
Ване мiстять пентагона.
2) Нехай ТСрати ![]() Вамiстять дiамант,
Вамiстять дiамант, ![]() . Аналогiчно, множина елементiв менших або c складаiться з елементiв {0,b,c}, iхня нижня границя не дасть a. Виходить, ТСрати
. Аналогiчно, множина елементiв менших або c складаiться з елементiв {0,b,c}, iхня нижня границя не дасть a. Виходить, ТСрати ![]() Ване мiстять дiаманта.
Ване мiстять дiаманта.
Можна зробити висновок, що ТСрати ![]() Вадистрибутивна.
Вадистрибутивна.
(**). Маiмо ![]() , тому
, тому ![]() , де
, де ![]() (по визначенню дистрибутивних напiвТСрат). Крiм того,
(по визначенню дистрибутивних напiвТСрат). Крiм того, ![]() Ваi нижньою границею елементiв
Ваi нижньою границею елементiв ![]() Ваi
Ваi ![]() .
.
Розглянемо iдеали, що мiстять елемент ![]() Ваi
Ваi ![]() Ва-
Ва- ![]() Ваi
Ваi ![]() . Тодi
. Тодi ![]() ВаØ ,тому що
ВаØ ,тому що ![]() , нижня границя елементiв a i , утримуiться там.
, нижня границя елементiв a i , утримуiться там.
Покажемо, що I(L) тАУ ТСрати, тобто iснують точнi нижня й верхня гранi для будь-яких A i B.
Покажемо, що ![]() збiгаiться з перетинанням iдеалiв A i B. По-перше,
збiгаiться з перетинанням iдеалiв A i B. По-перше, ![]() Ва- iдеал. Дiйсно,
Ва- iдеал. Дiйсно, ![]() Ваi
Ваi ![]() Вай
Вай ![]() ВаПо-друге, нехай iдеал
ВаПо-друге, нехай iдеал ![]() Ваi
Ваi ![]() . Тодi
. Тодi ![]() , тобто
, тобто ![]() Ва- точна нижня грань iдеалiв A i B, тобто
Ва- точна нижня грань iдеалiв A i B, тобто ![]() .
.
Тепер покажемо, що ![]() Вазбiгаiться з перетинанням всiх iдеалiв
Вазбiгаiться з перетинанням всiх iдеалiв ![]() , що мiстять A i B. Позначимо
, що мiстять A i B. Позначимо ![]() . Оскiльки
. Оскiльки ![]() Вадля
Вадля ![]()
![]() для
для ![]()
![]() , те C iдеал. По визначенню C вiн буде найменшим iдеалом, що мiстить A i B.
, те C iдеал. По визначенню C вiн буде найменшим iдеалом, що мiстить A i B.
(***). ![]() ВаНехай
ВаНехай ![]() ВатАУ верхнi дистрибутивнi напiвТСрати. Покажемо, що
ВатАУ верхнi дистрибутивнi напiвТСрати. Покажемо, що
![]() .
.
Нехай ![]() , тобто
, тобто ![]() Ва(мал.3), для деяких
Ва(мал.3), для деяких ![]()
Зрозумiло, що ![]() . По дистрибутивностi, iснують
. По дистрибутивностi, iснують ![]() Ватакi, що
Ватакi, що ![]() . Т.к. A тАУ iдеал, те
. Т.к. A тАУ iдеал, те![]() , тому що
, тому що ![]() . Аналогiчно,
. Аналогiчно, ![]() . Т.е.
. Т.е. ![]() . Точно також,
. Точно також, ![]() . Якщо
. Якщо ![]() , то легко показати, що
, то легко показати, що ![]() .
.
Довели, що ![]() Ва- iдеал. Очевидно, вiн i верхньою гранню iдеалiв A i B. Якщо C мiстить A i B, то C буде мiстити елементи
Ва- iдеал. Очевидно, вiн i верхньою гранню iдеалiв A i B. Якщо C мiстить A i B, то C буде мiстити елементи ![]() Вадля будь-яких
Вадля будь-яких ![]() , тобто
, тобто ![]() ВаТому
ВаТому ![]() , оскiльки
, оскiльки ![]() Ваi верхньою гранню iдеалiв A i B i втримуiться в будь-який верхнiй гранi.
Ваi верхньою гранню iдеалiв A i B i втримуiться в будь-який верхнiй гранi.
Тепер покажемо, що виконуiться рiвнiсть:
![]() .
.
![]() . Нехай
. Нехай ![]() , де
, де ![]() ,
,![]() .
. ![]() Ва, те
Ва, те![]() , звiдки
, звiдки ![]() Вай отже
Вай отже ![]() . Аналогiчно,
. Аналогiчно, ![]() , виходить,
, виходить, ![]()
![]() . Нехай
. Нехай ![]() ,де
,де ![]()
![]()
![]()
![]()
![]() .
.
Звiдси треба дистрибутивнiсть ТСрати ![]() .
.
![]()
![]() ВатАУ дистрибутивнi ТСрати,
ВатАУ дистрибутивнi ТСрати, ![]() . Тепер розглянемо iдеали, утворенi цими елементами:
. Тепер розглянемо iдеали, утворенi цими елементами:
![]()
(![]() ,буде нижньою границею для
,буде нижньою границею для ![]() ). Тому
). Тому ![]() , що й доводить дистрибутивнiсть напiвТСрат
, що й доводить дистрибутивнiсть напiвТСрат ![]() . :
. :
2. Стоуновий простiр
Визначення: Пiдмножина ![]() Ваверхнiх напiвТСрат
Ваверхнiх напiвТСрат ![]() Ваназиваiться коiдеалом, якщо
Ваназиваiться коiдеалом, якщо ![]() Ваз нерiвностi
Ваз нерiвностi ![]() Ватреба
Ватреба ![]() Вай
Вай ![]() Ваiснуi нижня границя
Ваiснуi нижня границя ![]() множини
множини ![]() , така, що
, така, що ![]() .
.
Визначення: РЖдеал ![]() ВанапiвТСрати
ВанапiвТСрати ![]() Ваназиваються простим, якщо
Ваназиваються простим, якщо ![]() Вай множина
Вай множина ![]() Ваi коiдеалом.
Ваi коiдеалом.
Надалi нам буде потрiбно лема Цорна, що i еквiвалентним твердженням аксiомi вибору.
Лема Цорна. Нехай A тАУ множина й X тАУ непуста пiдмножина множини P(A). Припустимо, що X маi наступну властивiсть: якщо C тАУ ланцюг в <![]() >, те
>, те ![]() . Тодi X маi максимальний елемент.
. Тодi X маi максимальний елемент.
Лема 2: Нехай ![]() ВатАУ довiльний iдеал i
ВатАУ довiльний iдеал i ![]() ВатАУ непустий коiдеал дистрибутивних верхнiх напiвТСрат
ВатАУ непустий коiдеал дистрибутивних верхнiх напiвТСрат ![]() . Якщо
. Якщо ![]() , то в напiвТСратах
, то в напiвТСратах ![]() Ваiснуi простий iдеал
Ваiснуi простий iдеал ![]() Ватакий, що
Ватакий, що ![]() Вай
Вай ![]() .
.
Доказ.
Нехай X тАУ множина всiх iдеалiв в L, що мiстять I i не пересiчних з D. Покажемо, що X задовольняi лемi Цорна.
Нехай C тАУ довiльний ланцюг в X i ![]() ВаЯкщо
ВаЯкщо ![]() , те
, те ![]() Вадля деяких
Вадля деяких ![]() ВаНехай для визначеностi
ВаНехай для визначеностi ![]() . Тодi
. Тодi ![]() Вай
Вай ![]() , тому що
, тому що ![]() Ва- iдеал. Тому
Ва- iдеал. Тому ![]() . Обернено, нехай
. Обернено, нехай ![]() , тодi
, тодi ![]() , для якогось
, для якогось ![]() ВаОдержуiмо
ВаОдержуiмо ![]() , звiдки
, звiдки ![]() .
.
Довели, що M тАУ iдеал, мабуть, що мiстить I i не пересiчний з D, тобто ![]() . По лемi Цорна X маi максимальний елемент, тобто максимальним iдеалом P серед утримуючих I i не пересiчних з D.
. По лемi Цорна X маi максимальний елемент, тобто максимальним iдеалом P серед утримуючих I i не пересiчних з D.
Покажемо, що P тАУ простiй. Для цього досить довести, що L\P i коiдеалом. Нехай ![]() L\P i
L\P i ![]() . Оскiльки
. Оскiльки ![]() , те
, те![]() , iнакше в противному випадку
, iнакше в противному випадку ![]() Вапо визначенню iдеалу. Отже,
Вапо визначенню iдеалу. Отже, ![]() . Якщо
. Якщо ![]() , то
, то ![]() Вай
Вай ![]() Вапересiчних з D у силу максимальностi P. Одержуiмо
Вапересiчних з D у силу максимальностi P. Одержуiмо ![]() Вай
Вай ![]() Вадля деяких елементiв
Вадля деяких елементiв ![]() . РЖснуi елемент
. РЖснуi елемент ![]() Ватакий, що
Ватакий, що ![]() Вай
Вай ![]() , по визначенню коiдеала, отже
, по визначенню коiдеала, отже ![]() Вай
Вай ![]() Вадля деяких
Вадля деяких ![]() ВаПомiтимо, що
ВаПомiтимо, що ![]() Вай
Вай ![]() Ване лежать в P, тому що в противному випадку
Ване лежать в P, тому що в противному випадку ![]() .
.
Далi, ![]() , тому
, тому ![]() Вадля деяких
Вадля деяких ![]() Ваi
Ваi ![]() . Як i колись
. Як i колись ![]() . Крiм того
. Крiм того ![]() , тому
, тому ![]() Ва- нижня грань елементiв a i b, що не лежить в P. :
Ва- нижня грань елементiв a i b, що не лежить в P. :
Надалi, через ![]() Вабудемо позначати дистрибутивнi верхнi напiвТСрати з нулем, через
Вабудемо позначати дистрибутивнi верхнi напiвТСрати з нулем, через ![]() множину всiх простих iдеалiв напiвТСрати
множину всiх простих iдеалiв напiвТСрати ![]() .
.
Множини виду ![]() Вапредставляють елементи напiвТСрат
Вапредставляють елементи напiвТСрат ![]() Вау ч.в. множинi
Вау ч.в. множинi ![]() Ва(тобто
Ва(тобто ![]() ). Зробимо всi такi множини вiдкритими в деякiй топологii.
). Зробимо всi такi множини вiдкритими в деякiй топологii.
Позначимо через ![]() Ватопологiчний простiр, певний на множинi
Ватопологiчний простiр, певний на множинi ![]() . Простiр SpecL будемо називати стоуновим простором напiвТСрат L.
. Простiр SpecL будемо називати стоуновим простором напiвТСрат L.
Лема 3: Для будь-якого iдеалу I напiвТСрати L покладемо:
![]()
Тодi множини виду ![]() Вавичерпують всi вiдкритi множини в стоуновом просторi SpecL.
Вавичерпують всi вiдкритi множини в стоуновом просторi SpecL.
Доказ.
Потрiбно перевiрити виконання аксiом топологiчного простору.
1) Розглянемо iдеал, утворений 0. Тодi
![]() ,
,
але 0 лежить у будь-якому iдеалi, а значить ![]() .
.
2) Вiзьмемо довiльнi iдеали ![]() Вай
Вай ![]() ВанапiвТСрати
ВанапiвТСрати ![]() Вай розглянемо
Вай розглянемо
![]()
![]()
Нехай ![]() . Тодi iснують елементи a
. Тодi iснують елементи a![]() i
i![]() ВаЗвiдси треба, що
ВаЗвiдси треба, що ![]() , де L\P тАУ коiдеал. По визначенню коiдеала iснуi елемент d
, де L\P тАУ коiдеал. По визначенню коiдеала iснуi елемент d![]() такий, що
такий, що![]() Вай
Вай ![]() , виходить,
, виходить,![]() . Так як.
. Так як. ![]() , отже,
, отже, ![]() . Одержуiмо, що
. Одержуiмо, що ![]() .
.
Зворотне включення очевидно.
2) Нехай ![]() Ва- довiльне сiмейство iдеалiв. Через
Ва- довiльне сiмейство iдеалiв. Через ![]() Вапозначимо множину всiх точних верхнiх граней кiнцевого числа елементiв, що i представниками сiмейства
Вапозначимо множину всiх точних верхнiх граней кiнцевого числа елементiв, що i представниками сiмейства ![]() . Покажемо, що
. Покажемо, що ![]() Ва- iдеал. Нехай
Ва- iдеал. Нехай ![]() , тодi
, тодi ![]() , де
, де ![]() Вадля деякого iдеалу
Вадля деякого iдеалу ![]() . Тодi
. Тодi ![]() Валежить в iдеалi
Валежить в iдеалi ![]() , отже,
, отже, ![]() Ваi
Ваi ![]() , тобто
, тобто ![]() . Обернено очевидно.
. Обернено очевидно.
Довели, що ![]() Ва- iдеал. Тепер розглянемо довiльне об'iднання.
Ва- iдеал. Тепер розглянемо довiльне об'iднання.
![]() Ва■
Ва■
Лема 4: Пiдмножини виду ![]() Вапростору
Вапростору ![]() Ваможна охарактеризувати як компактнi вiдкритi множини.
Ваможна охарактеризувати як компактнi вiдкритi множини.
Доказ.
![]() ВаДiйсно, якщо сiмейство
ВаДiйсно, якщо сiмейство ![]() Вавiдкритих множин покриваi множина
Вавiдкритих множин покриваi множина ![]() , тобто
, тобто ![]()
![]() , те
, те ![]() ВаЗвiдси треба, що
ВаЗвiдси треба, що ![]() для деякоi кiнцевоi пiдмножини
для деякоi кiнцевоi пiдмножини ![]() , тому
, тому ![]()
![]() . Таким чином, множина
. Таким чином, множина ![]() Вакомпактно.
Вакомпактно.
![]() ВаНехай вiдкрита множина r(I) компактно, тодi
ВаНехай вiдкрита множина r(I) компактно, тодi ![]() Вай можна видiлити кiнцеве пiд покриття
Вай можна видiлити кiнцеве пiд покриття ![]() Вадля деяких
Вадля деяких ![]() .
.
Покажемо, що I породжуiться елементом ![]() .
.
Припустимо, що це не так, i в iдеалi I найдеться елемент не лежачий в. ![]() ВаТодi [b) тАУ коiдеал, не пересiчний с.
ВаТодi [b) тАУ коiдеал, не пересiчний с.![]() По лемi 2 найдеться простий iдеал P утримуючий
По лемi 2 найдеться простий iдеал P утримуючий ![]() Ваi не пересiчний з [b). Одержуiмо,
Ваi не пересiчний з [b). Одержуiмо, ![]() , тому що
, тому що ![]() Ва(тобто
Ва(тобто ![]() ), але
), але ![]() , тому що
, тому що ![]()
![]() , протирiччя. Отже, компактною вiдкритою множиною r(I) буде тiльки у випадку, якщо
, протирiччя. Отже, компактною вiдкритою множиною r(I) буде тiльки у випадку, якщо ![]() Ва- головний iдеал.
Ва- головний iдеал.
Пропозицiя 5:Простiр ![]() Ваi
Ваi ![]() - простором.
- простором.
Доказ.
Розглянемо два рiзних простих iдеали ![]() Вай Q. Хоча б один не втримуiться в iншому. Допустимо для визначеностi, що
Вай Q. Хоча б один не втримуiться в iншому. Допустимо для визначеностi, що ![]() . Тодi r(P) мiстить Q, але не мiстить P, тобто SpecL i
. Тодi r(P) мiстить Q, але не мiстить P, тобто SpecL i ![]() - простором. :
- простором. :
Теорема 6: Стоуновий простiр ![]() Вавизначаi напiвТСрати
Вавизначаi напiвТСрати ![]() Ваз точнiстю до iзоморфiзму.
Ваз точнiстю до iзоморфiзму.
Доказ.
Потрiбно показати, що двоi напiвТСрат ![]() Ваi
Ваi ![]() Ваiзоморфнi тодi й тiльки тодi, коли простори
Ваiзоморфнi тодi й тiльки тодi, коли простори ![]() Вай
Вай ![]() Вагомеоморфни.
Вагомеоморфни.
![]() ВаОчевидно, якщо ТСрати iзоморфнi, то простору, утворенi цими напiвТСратами будуть збiгатися.
ВаОчевидно, якщо ТСрати iзоморфнi, то простору, утворенi цими напiвТСратами будуть збiгатися.
![]() ВаНехай
ВаНехай ![]() Ваi
Ваi ![]() Вагомеоморфни (
Вагомеоморфни (![]() ) i
) i ![]() . Тодi a визначаi компактна вiдкрита множина r(a)
. Тодi a визначаi компактна вiдкрита множина r(a)![]() . Множинi r(a) вiдповiдаi компактна вiдкрита множина
. Множинi r(a) вiдповiдаi компактна вiдкрита множина ![]() , з однозначно певним елементом
, з однозначно певним елементом ![]() Вапо лемi 4. У такий спосiб одержуiмо вiдображення
Вапо лемi 4. У такий спосiб одержуiмо вiдображення ![]() :
: ![]() , при якому
, при якому ![]() . Покажемо, що
. Покажемо, що ![]() Ва- iзоморфiзм ТСрат. Якщо a,b тАУ рiзнi елементи з
Ва- iзоморфiзм ТСрат. Якщо a,b тАУ рiзнi елементи з ![]() , те
, те![]() , отже,
, отже, ![]() , тому
, тому ![]() Вай
Вай ![]() Ва- iн'iкцiя.
Ва- iн'iкцiя.
Для довiльного ![]() Вавiдкритiй множинi
Вавiдкритiй множинi ![]() Вавiдповiдаi
Вавiдповiдаi ![]() Вай очевидно
Вай очевидно![]() , що показуi сюрективнiсть
, що показуi сюрективнiсть ![]() .
.
Нехай a,b тАУ довiльнi елементи з ![]() . Помiтимо, що
. Помiтимо, що ![]() . Вiдкритiй множинi
. Вiдкритiй множинi ![]() Вапри гомеоморфiзмi
Вапри гомеоморфiзмi ![]() Вавiдповiдаi вiдкрита множина
Вавiдповiдаi вiдкрита множина ![]() , а
, а ![]() Вавiдповiдаi
Вавiдповiдаi ![]() . Отже,
. Отже, ![]() =
=![]() . Оскiльки
. Оскiльки ![]() =
=![]() , те
, те![]() , тобто
, тобто ![]()
Висновок
алгебра множина грань грата топологiчний
Дистрибутивнi ТСрати i одним з основних алгебраiчних об'iктiв. У данiй роботi розглянута частково впорядкована множина P(L) простих iдеалiв. Вона даi нам багато iнформацii про дистрибутивнi ТСрати L, але вона не може ii повнiстю охарактеризувати. Тому, для того, щоб множина P(L) характеризувало ТСрати L, необхiдно надiлити ii бiльше складною структурою. Стоун [1937] задав на множинi P(L) топологiю. У цiй роботi метод розглянутий у трохи бiльш загальному видi.
Лiтература
1. Биргкоф Г. Теорiя ТСрат. тАУ К., 2003.
2. Гретцер Г. Загальна теорiя ТСрат. тАУ К., 2005
3. Чермних В.В. Пiвкiльця. тАУ К., 1997.
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы