Застосування подвiйних iнтегралiв

Содержание

1. Замiна змiнних у подвiйному iнтегралi. Подвiйний iнтеграл у полярних координатах

2. Застосування подвiйних iнтегралiв до задач геометрii

3. Застосування подвiйних iнтегралiв до задач механiки

1. Замiна змiнних у подвiйному iнтегралi. Подвiйний iнтеграл у полярних координатах

Нехай функцiя Ванеперервна в деякiй замкненiй i обмеженiй областi ,тодi iснуi iнтеграл

Припустимо, що за допомогою формул

Ва(1)

ми переходимо в iнтегралi Вадо нових змiнних Вата . Вважатимемо, що з формул (1) однозначно можна визначити та :

. (2)

Згiдно з формулами (2), кожнiй точцi Ваставиться у вiдповiднiсть деяка точка на координатнiй площинi з прямокутними координатами Ваi .

Нехай множина всiх точок Ваутворюi обмежену замкнену область . Формули (1) називаються формулами перетворення координат, а формули (2) - формулами оберненого перетворення.

Справедлива така теорема.

Теорема. Якщо перетворення (2) переводить замкнену обмежену область в замкнену обмежену область Ваi i взаiмно однозначним, i якщо функцii (1) мають в областi неперервнi частиннi похiднi першого порядку i вiдмiнний вiд нуля визначник

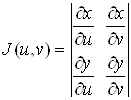, (3)

а функцiя Ванеперервна в областi , то справедлива така формула замiни змiнних

. (4)

Функцiональний визначник називаiться визначником Якобi або якобiаном.

Таким чином, виконуючи замiну змiнних в iнтегралi Ваза формулами (1), ми маiмо елемент площi Вав координатах Вазамiнити елементом площi Вав координатах Ваi стару область iнтегрування Вазамiнити вiдповiдною iй областю .

Розглянемо замiну декартових координат Ваполярними Ваза вiдомими формулами. Оскiльки

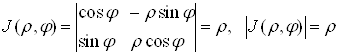То формула (3) набираi вигляду

Ва(4)

де область Вазадана в декартовiй системi координат , а Ва- вiдповiдна iй область в полярнiй системi координат.

У багатьох випадках формулу (4) доцiльно застосовувати тодi, коли пiдiнтегральна функцiя або рiвняння границi областi Вамiстить суму , оскiльки ця сума в полярних координатах маi досить простий вигляд:

Якщо область Ва(рис.1, а) обмежена променями, якi утворюють з полярною вiссю кути Вата Ваi кривими Вата , то полярнi координати областi Вазмiнюються в межах , Ва(рис.1, б). Тому формулу (4) можна записати у виглядi

Ва(5)

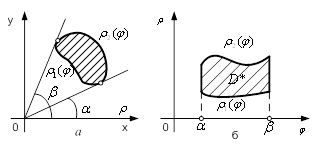
Рисунок 1 - Область: а) ; б)

подвiйний iнтеграл полярна координата

Якщо область Ваохоплюi початок координат, тобто точка Ваi внутрiшньою точкою областi , то

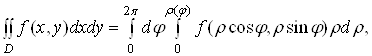Ва(6)

де Ва- полярне рiвняння межi областi .

Приклади

1. Обчислити iнтеграл , якщо область Ва- паралелограм,

обмежений прямими Ва(рис.1, а).

РозвтАЩязання

Безпосереднi обчислення цього iнтеграла надто громiздке, тому що як в напрямi осi Ватак i в напрямi осi Ваобласть Вапотрiбно спочатку розбити на три областi, а потiм обчислювати три подвiйних iнтеграли.

Виконаiмо таку замiну змiнних: , тодi прямi Вата Вав системi Вапереходять в прямi Вата Вау системi Ва(рис.1, б), а прямi Вата Вавiдповiдно в прямi Вата .

Таким чином, область Ва(паралелограм) переходить у системi Вав прямокутник .

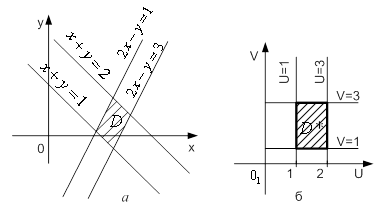
Рисунок 2 - Область: а) ; б)

Далi маiмо

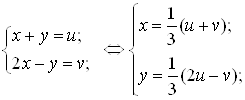
За формулою (3)

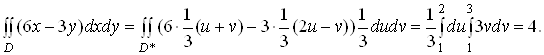
2. У подвiйному iнтегралi , де Ва- круг, обмежений колом , перейти до полярних координат з полюсом в точцi , i обчислити отриманий iнтеграл.

РозвтАЩязання

Область Вазображена на рис.2.

Рiвняння, якi повтАЩязують Ваi полярнi координати Ваз полюсом у точцi , мають вигляд , причому видно, що кут Вазмiнюiться в межах вiд Вадо .

Рисунок 3 - Область

Пiдставивши вирази для Ваi Вав рiвняння кола, отримаiмо , звiдки Ваабо . Цi двi кривi на площинi Вапри Ваобмежують область , яка i прообразом областi Вапри вiдображеннi. Якобiан Вавiдображення дорiвнюi . Пiдiнтегральна функцiя Вау нових змiнних дорiвнюi . За формулою (3) маiмо

Одержаний подвiйний iнтеграл за областю Вазводимо до повторного:

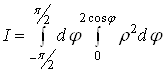
i обчислюiмо повторний iнтеграл, застосовуючи формулу Ньютона - Лейбнiца:

2.
Застосування подвiйних iнтегралiв до задач геометрii

1. Площа плоскоi фiгури. Якщо в площинi Вазадана фiгура, що маi форму обмеженоi замкненоi областi , то площа Вацiii фiгури знаходиться, як вiдомо, за формулою:

2. Об'iм тiла. Об'iм цилiндричного тiла, твiрнi якого паралельнi осi Ваi яке обмежене знизу областю Ваплощини , а зверху - поверхнею , де функцiя Ванеперервна та невiд'iмна в областi , знаходиться за формулою (2):

3. Площа поверхнi. Якщо поверхня ,задана рiвнянням

Ва(7)

проектуiться на площину Вав область Ва(рис.3) i функцii , , Ванеперервнi в цiй областi, то площу Ваповерхнi знаходять за формулою

Ва(8)

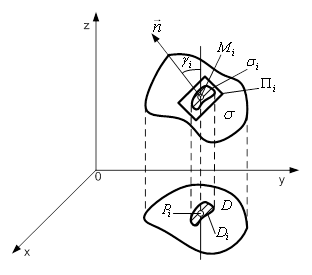
Рисунок 4 - Поверхня

Виведемо цю формулу. РозiбтАЩiмо довiльним способом область Вана частин , якi не мають спiльних внутрiшнiх точок i площi яких дорiвнюють . У кожнiй частинi Вавiзьмемо точку ; на поверхнi Ваiй вiдповiдатиме точка , де . Через точку проведемо дотичну площину Ва[3]

На площинi Вавидiлимо ту ii частину, яка проектуiться на площину в область . Позначимо цю частину дотичноi площини через , а ii площу - через . Складемо суму

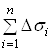. (9)

Границю Васуми (9), коли найбiльший з дiаметрiв Ваобластей Вапрямуi до нуля, назвемо площею поверхнi (7), тобто за означенням покладемо

. (10)

Обчислимо цю границю. Оскiльки область , яка маi площу , проектуiться в область Ваз площею , то , де Ва- кут мiж площинами та Ва(рис.3), тому .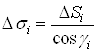

Але гострий кут дорiвнюi куту мiж вiссю i нормаллю до дотичноi площини, тобто куту мiж векторами та . Знайдемо за формулою (4)

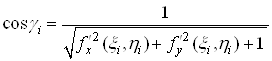Отже,

Пiдставляючи значення Вав (10), отримуiмо

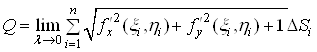Пiд знаком границi маiмо iнтегральну суму, складену для неперервноi в областi функцii . Ця функцiя iнтегровна в областi , тому границя у формулi (10) iснуi i дорiвнюi подвiйному iнтегралу (8).

3. Застосування подвiйних iнтегралiв до задач механiки

1. Маса пластини. Нехай на площинi Вамаiмо матерiальну пластину, яка маi форму обмеженоi замкненоi областi , в кожнiй точцi якоi густина визначаiться неперервною функцiiю . Маса такоi пластини визначаiться за формулою (1.8):

2. Центр маси пластини. Статичнi моменти. Нехай матерiальна пластина в площинi маi форму областi , густина пластини в точцi дорiвнюi , де Ва- неперервна функцiя в областi ВаРозiб'iмо область на частини ,виберемо в кожнiй з них довiльну точку Ваi наближено вважатимемо, що маса Вачастини Вадорiвнюi , де Ва- площа областi . Коли вважати, що кожна з цих мас зосереджена в точцi , то пластину можна розглядати як систему цих матерiальних точок. Тодi координати та центра маси пластини наближено визначатимуться рiвностями

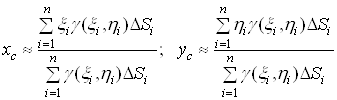Щоб знайти точнi значення координат, перейдемо в цих формулах до границi при . Тодi iнтегральнi суми перейдуть у подвiйнi iнтеграли i координати центра маси пластини визначатимуться формулами

. (11)

Величини

Ва(12)

називаються статичними моментами пластини вiдносно осi Вата .

Враховуючи формули (8), (11) i (12), координати центра мас можна записати у виглядi

Якщо пластина однорiдна, тобто маi сталу густину , то у формулах (1.8), (11) i (12) слiд покласти .

3. Моменти iнерцii пластини. Вiдомо, що момент iнерцii матерiальноi точки вiдносно деякоi осi дорiвнюi добутку маси точки на квадрат ii вiдстанi вiд цiii осi, а момент iнерцii системи матерiальних точок вiдносно однiii i тiii самоi осi дорiвнюi сумi моментiв iнерцii всiх точок системи.

Нехай матерiальна пластина маi форму областi у площинi ,а неперервна функцiя Вавизначаi густину в кожнiй точцi цiii пластини. Розiб'iмо область Вана частини , площi яких дорiвнюють , i виберемо в кожнiй з цих частин довiльну точку . Замiнимо пластину системою матерiальних точок з масами . Якщо пластину розглядати як систему цих матерiальних точок, то моменти iнерцii пластини вiдносно осi Вата вiдносно наближено визначатимуться за формулами

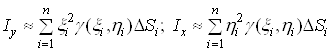Перейшовши до границi в кожнiй iз сум при , отримуiмо точнi формули для обчислення моментiв iнерцii розглядуваноi пластини вiдносно координатних осей:

. (13)

Знайдемо момент iнерцii Вапластини вiдносно початку координат.

Враховуючи, що момент iнерцii матерiальноi точки з масою вiдносно початку координат дорiвнюi , аналогiчно отримуiмо, що

. (14)

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы