Ваи интегралы Коши по плоскости 
, также была рассмотрена аналитическая функция, аналитическая зависимость от параметра.1. Регулярность интегралов, зависящих от параметра
2. Интеграл коши на кривой
3. Интеграл коши на области
3.1 Аналитическая зависимость от параметра
3.2 Существование производных всех порядков у аналитической функции
3.3 Вывод формулы Коши
3.2 Следствия из формулы Коши
Заключение
Список литературы
Понятие ВлинтегралВ» непосредственно связано с интегральным исчислением − разделом математики, занимающимся изучением интегралов, их свойств и методов вычисления. Вместе с дифференциальным исчислением интегральное исчисление составляет основу математического анализа.
Так как целью моей прошлой курсовой работы являлось изучение некоторых аспектов темы, таких как интегрирование и дифференцирование интегралов, зависящих от параметра.
Цель данной курсовой работы является изучение новых аспектов по теме Влинтегралы, зависящие от параметровВ» и накопление материалов для следующих работ по данной тематике.
В данной курсовой работе я рассмотрел интегралы Коши по кривой Ваи интегралы Коши по плоскости , также была рассмотрена аналитическая функция, аналитическая зависимость от параметра.
Для достижения цели необходимо решить следующие задачи:
В· Найти и изучить литературу по данной теме
В· Накопить и систематизировать полученную информацию по теме
В· Изучить основные понятия.
Объектом исследования являются различные виды интегралов зависящих от параметра в курсе ВУЗов.
В работе использованы следующие методы исследования:
1. Анализ научной литературы по теме Влинтегралы, зависящие от параметровВ»
2. Синтез полученных знаний
3. Обобщение полученных знаний
Работа насчитывает 26 страницы, состоит из введения, четырех глав, заключения, библиографического списка используемой литературы и содержащего 10 наименований, вспомогательные указатели, а также содержит 2 иллюстрации.
Рассмотрим интеграл
.(1)
Теорема 1. [7, c. 111] Пусть выполнены условия:
1) Ва- конечная кусочно-гладкая кривая;
2) функция 
Ванепрерывна по 
Вапри 
, где 
Ва- область в комплексной плоскости;
3) при каждом фиксированном 
Вафункция Варегулярна по 
Вав области .
Тогда интеграл (1) есть регулярная в области функция.
Доказательство. В силу условий 1, 2 функция 
Ванепрерывна в области . Возьмем произвольную точку 
Ваи построим круг 
, который содержит точку 
Ваи лежит внутри . Применим теорему Морера. Пусть 
Ва- замкнутая кривая, лежащая в круге . Тогда
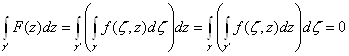,(2)
так как порядок интегрирования можно переставить, а интеграл по Варавен нулю (интегральная теорема Коши). По теореме Морера функция Варегулярна в круге ; следовательно, Варегулярна в области .
Следствие 1. Пусть Ва- неограниченная кусочно-гладкая кривая, пусть выполнены условия 2, 3 и следующее условие:
4) интеграл (1) сходится равномерно по 
, где 
Ва- любая замкнутая подобласть области .
Тогда функция Варегулярна в области .
Следствие 2. Пусть условия 1, 3 выполнены, но функция Ваможет имеет особенности в концах кривой . Если функция Ванепрерывна по Вапри 
, 
Ване принадлежит концам Ваи выполнено условие 4, то функция Варегулярна в области .
Доказательство следствий 1 и 2 проводится точно также, как и в теореме 1; интегралы в (2) можно переставлять в силу равномерной сходимости интеграла (1).
Теорема 2. [7, c.112] Пусть выполнены условия теоремы 1. Тогда
.(3)
Доказательство. Пусть Ва- круг 
, лежащий в области Ваи Ва- его граница. Тогда при 
Ваимеем
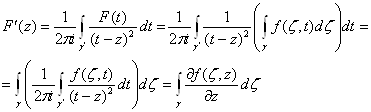
Перестановка порядка интегрирования возможна в силу непрерывности подынтегральной функции и конечности кривых 
.
Замечание. Теорема 2 остается в силе, если выполнены условия следствия 1 или 2, и интеграл (3) сходится равномерно по , где Ва- любая замкнутая подобласть области .
Наиболее употребляемыми в математической физике интегральными преобразованиями являются преобразования Лапласа, Фурье и Меллинга.
Пусть функция 
Ваопределена на полуоси 
. Ее преобразованием Лапласа называется функция
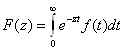.(4)
Теорема 3. [7, c.113] Пусть функция Ванепрерывна при Ваи удовлетворяет оценке
(5)
Тогда ее преобразование Лапласа Ваесть функция, регулярная в полуплоскости 
.
Доказательство. Воспользуемся следствием 1 из теоремы 1. Условия 2, 3 теоремы 1 выполнены. Пусть 
. Тогда
.
Так как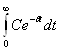 
сходится, то по признаку Вейерштрасса интеграл (4) сходится равномерно по Вапри 
Ваи функция Варегулярна в этой полуплоскости. В силу произвольности 
Вафункция Варегулярна при .
Преобразованием Фурье функции Ваопределенной на действительной оси, называется функция
(6)
Теорема 4. [7, c.113] Пусть функция Ванепрерывна при 
Ваи удовлетворяет оценкам
, (7)
где 
. Тогда ее преобразование Фурье Ваесть функция, регулярная в полосе 
.
Доказательство. Разобьем интеграл (6) на два интеграла:
.
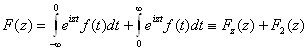В силу условия (7) и теоремы 3 функция 
Варегулярна в полуплоскости 
, а функция 
Ва- в полуплоскости 
, что и доказывает теорему.
В частности, если функция Вафинитна, т.е. 
Вапри 
, и непрерывна при 
, то ее преобразование Фурье является целой функцией. Это следует из теоремы 1, поскольку в этом случае
.
Преобразованием Меллина функции , определенной на полуоси , называется функция
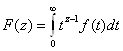(8)
Здесь 
.
Теорема 5. [7, c.114] Пусть функция Ванепрерывна при 
Ваи удовлетворяет оценкам:
, (9)
где 
. Тогда ее преобразование Меллина является функцией, регулярной в полосе 
.
Доказательство. Разобьем интеграл (8) на два интеграла
.
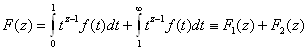Пусть 
, 
Ваи ; тогда
.
Так как 
Васходится при , то, по признаку Вейерштрасса, интеграл Васходится равномерно по Вапри . В силу следствия 2 функция Варегулярна в полуплоскости 
.
Далее, при 
, 
Ваи Ваимеем
Из сходимости интеграла 
Ваи следствия 1 вытекает, что функция Варегулярна в полуплоскости 
.
Преобразования Фурье и Меллина связаны следующим соотношением:
, (10)
где 
Ва- преобразование Меллина, а 
- преобразование Фурье функции 
. Действительно, делая замену переменной 
, получаем
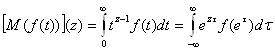
(мы предполагаем, что все интегралы сходятся). Последний интеграл совпадает с правой частью формулы (10).
В частности, с помощью соотношения (10) можно вывести теорему 5 из теоремы 4.
(11)
Интеграл называется интегралом типа Коши. Исследуем его аналитические свойства в предположении, что функция 
Ванепрерывна на кривой .
1. Пусть Ва- конечная кривая. Тогда дополнение к Васостоит из конечного или бесконечного числа областей. В каждой из этих областей интеграл типа Коши является регулярной функцией в силу теоремы 1.Однако эти регулярные функции, вообще говоря, различны, т.е. не являются аналитическими продолжениями друг друга. Например,
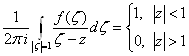
Покажем, что функция, представленная интегралом (11) регулярна в бесконечно удаленной точке. Делая замену 
Ваи полагая 
, получаем
.
Так как Ва- конечная кривая, то знаменатель 
Вапри достаточно малых 
Ваи функция 
Варегулярна в точке 
Вав силу теоремы 1.
2. Пусть Ва- бесконечная кривая. Ограничимся, для простоты случаем, когда Ва- вещественная ось; тогда
(12)
Пусть функция Ваудовлетворяет оценке
(13)
Покажем, что тогда формула (12) определяет две функции 
, которые регулярны в полуплоскостях 
, 
Васоответственно. Воспользуемся следствием 1.Рассмотрим случай . Пусть 
Валежит в полуполосе 
: 
, где 
, 
. При вещественных 
Ваи при 
Ваимеем 
, если 
. Следовательно,
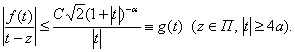
Поскольку интеграл 
Васходится, то по признаку Вейерштрасса интеграл Васходится равномерно по . В силу следствия 1 функция Варегулярна при ; так как Ваможно выбрать сколь угодно большим, а Ва- сколь угодно малым, то интеграл (12) представляет функцию 
, регулярную в верхней полуплоскости. Аналогично доказывается, что интеграл (12) представляет функцию 
, регулярную в нижней полуплоскости.
Пример 1. [7, c.119] Пусть функция 
Ванепрерывна на полуоси Ваи удовлетворяет оценке . Тогда интеграл типа Коши представляет функцию, регулярную в плоскости с разрезом по полуоси 
.
3. Если функция Варегулярная на контуре интегрирования , то интеграл типа Коши допускает аналитическое продолжение через точки контура. Прием, который при этом используется, заключается в том, что мы сдвигаем контур интегрирования.
Пример 2. [7, c.119] Пусть
.
Функция Варегулярна в круге 
. Покажем, что функцию Ваможно аналитически продолжить на всю комплексную плоскость . Положим при 
.
Функция 
Варегулярна в круге 
. Покажем, что
.
тем самым наше утверждение будет доказано. Подынтегральная функция 
Варегулярна в кольце 
, если 
, так как функция 
Варегулярна при всех 
.
Следовательно, в силу интегральной теоремы Коши интегралы по окружностям 
Ваи 
Ваот функции Варавны при Вачто и требовалось доказать.
Этот пример допускает следующее обобщение. Рассмотрим интеграл Ватипа коши (11), где Ва- простая замкнутая кривая. Тогда этот интеграл определяет функцию, регулярную в области 
, лежащей внутри .
Пусть функция Варегулярна в замкнутой области , ограниченной кривыми Ваи , где Ва- простая замкнутая кривая, и Валежит внутри . Тогда формула
дает аналитическое продолжение функции Вав область , лежащую внутри . Действительно, функция 
Варегулярна в области , если 
, так что в силу интегральной теоремы Коши
.
Интеграл в левой части этой формулы задает функцию, регулярную в , а интеграл в правой части равен . Следовательно, 
, и наше утверждение доказано.
Аналогичный метод применим к интегралам вида (12).
Теорема 6. [7, c.120] Пусть функция Варегулярна в полосе 
Ваи удовлетворяет условию
.
Тогда интеграл (2) допускает аналитическое продолжение в полуплоскость 
Ваи это продолжение 
Вадается формулой
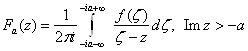
Аналитическая зависимость от параметра. Рассматривая интеграл Коши, мы видим, что подынтегральная функция зависит от двух комплексных переменных: переменной интегрирования 
и фиксированного значения переменной 
. Тем самым интеграл Коши является интегралом, зависящим от параметра. Естественно поставить вопрос об общих свойствах интегралов по комплексной переменной, зависящих от параметра.
Пусть задана функция двух комплексных переменных 
, однозначно определенная для значений комплексной переменной 
Ваиз области Ваи для значения комплексной переменной 
, принадлежащих некоторой кусочно-гладкой кривой С. Взаимное расположение области Ваи кривой 
может быть совершенно произвольно. Пусть функция двух комплексных переменных Ваудовлетворяют следующим условиям:
a) Функция Вапри любом значении 
Ваявляется аналитической функцией Вав области .
b) Функция Ваи ее производная 
Ваявляются непрерывными функциями по совокупности переменных 
Вапри произвольном изменении Вав области Ваи Вана кривой
Условие (
) означает, что действительная и мнимая части функции Ванепрерывны по совокупности переменных 
.
Очевидно, что при сделанных предположениях интеграл от функции Вапо кривой Васуществует при любом 
Ваи является функцией комплексной переменной 
(14)
Естественно поставить вопрос о свойствах функции . Оказывается, что при сделанных предположениях относительно функции Вафункция Ваявляется аналитической функцией комплексной переменной Вав области , причем производную функции Ваможно вычислять при помощи дифференцирования под знаком интеграла.
Для того чтобы доказать это утверждение, рассмотрим криволинейный интеграл
.
Так как, по предположению, функции 
Ваи 
Ваобладают частными производными по 
Ваи 
, непрерывными по совокупности переменных, то частные производные функции 
Вапо переменным , Васуществуют и их можно вычислить при помощи дифференцирования под знаком интеграла (14):
Сами функции 
Ваи 
Ваявляются непрерывными функциями переменных , Вав области Ва. На основании аналогичных свойств функции 
Ваи используя условия Коши-Римана для функции , получим
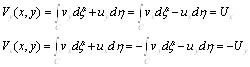(15)
Таким образом, для Вавыполнены условия Коши-Римана (частные производные функции Ваи непрерывны и связаны соотношениями (15)), что и доказывает аналитичность Вав области .
Заметим, что
(16)
Отсюда следует возможность вычисления производной от интеграла путем дифференцирования подынтегральной функции по параметру. При этом, если 
Ваудовлетворяет тем же условиям () и (), что и , то Ватакже является аналитической функцией в области .
Рассмотренное свойство интегралов, зависящих от параметра, позволяет установить важные характеристики аналитических функций. Как мы видели, значение функции , аналитической в некоторой области , ограниченной контуром 
, и непрерывной в замкнутой области 
, во внутренних точках этой области моет быть выражено через граничные значения с помощью интеграла Коши:
.(17)
Рассмотрим в области Ванекоторую замкнутую подобласть , расстояние всех точек которой от границы Ваобласти Вабольше некоторого положительного числа 
. Функция
является аналитической функцией Вав области 
Вапричем ее частная производная 
Вав этой области является непрерывной функцией своих аргументов. Тем самым в силу общих свойств интегралов, зависящих от параметра, во внутренних точках области Вапроизводная 
Ваможет быть представлена в виде
(18)
Интеграл (18) является интегралом, зависящим от параметра, причем его подынтегральная функция обладает теми же свойствами, что и подынтегральная функция интеграла (17). Следовательно, Ваявляется аналитической функцией Вав области Вапричем для ее производной справедлива формула
.(19)
Так как для любой внутренней точки Ваобласти Ваможет быть построена соответствующая замкнутая подобласть Вато формулы (18) и (19) справедливы в любой точке . Имеет место и более общая теорема.
Теорема 7. [6, c.58] Пусть функция Ваявляется аналитической в области и непрерывной в замкнутой области . Тогда во внутренних точках области Васуществует производная любого порядка функции , причем для нее имеет место формула
(20)
Для доказательства этой теоремы достаточно повторить предыдущие рассуждения соответствующее число раз. Итак, если функция является аналитической функцией в области , то в этой области функция Ваобладает непрерывными производными всех порядков. Это свойство аналитической функции комплексной переменной существенным образом отличает ее от функции действительной переменной, имеющей непрерывную первую производную в некоторой области. В последнем случае из существования первой производной, вообще говоря, не следует существование высших производных.
Рассмотрим ряд важных следствий установленного свойства аналитической функции комплексной переменной.
Теорема 8(Морера). [6, c.59]Пусть функция Ваявляется непрерывной в односвязной области Ваи интеграл от Вапо любому замкнутому контуру, целиком принадлежащему , равен нулю. Тогда Ваявляется аналитической функцией в области .
Доказательство. Было доказано, что при условиях теоремы функция
,
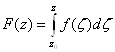где , Ва- произвольные точки области , а интеграл берется по любому пути, соединяющему эти точки в области , является аналитической в этой области функцией, причем 
. Но, как только что было установлено, производная аналитической функции также является аналитической функцией, т. е. существует непрерывная производная функции 
, а именно функция 
, что и доказывает теорему.
Отметим, что теорема 1.10 является в определенном смысле обратной по отношению к теореме Коши. Ее легко обобщить и на многосвязные области.
Теорема 9(Лиувилля). [6, c.59] Пусть на всей комплексной плоскости функция Ваявляется аналитической, а ее модуль равномерно ограничен. Тогда эта функция Ватождественно равна постоянной.
Доказательство. Запишем значение производной Вав произвольной точке 
Вапо формуле (18):
,
причем будем вести по окружности некоторого радиуса 
Вас центром в точке . т.е. 
. По условию теоремы существует такая константа 
, что 
Ванезависимо от . Поэтому
.
Так как радиус Ваможно выбрать сколь угодно большим, а Ване зависит от , то 
. В силу произвольности выбора точки Вазаключаем, что 
Вана всей комплексной плоскости. Отсюда следует, что 
.
Пусть функция Ваявляется аналитической в односвязной области , ограниченной контуром . Возьмем произвольную внутреннюю точку Ваи построим замкнутый контур , целиком лежащий в Ваи содержащий точку Вавнутри себя. Рассмотрим вспомогательную функцию
(21)
Функция 
, очевидно, является аналитической функцией всюду в области , за исключением точки . Поэтому, если мы в области Вавозьмем такой замкнутый контур , лежащий внутри , чтобы точка Вапопала внутрь области, ограниченной контуром , то функция Вабудет аналитической в двухсвязной области 
, заключенной между контурами Ваи . Согласно теореме Коши интеграл от функции Вапо кривой 
Варавен нулю:
Изменив направление интегрирования во втором интеграле, это равенство можно переписать в виде
(22)
Поскольку интеграл, стоящий слева, не зависит от выбора контура Вато этим свойством обладает и интеграл, стоящий справа. Для дальнейших рассмотрений удобно в качестве контура интегрирования Вавыбрать окружность 
некоторого радиуса 
Вас центром в точке Ва(Рис. 1). Положив 
,имеем.
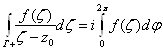
Последний интеграл преобразуем следующим образом:
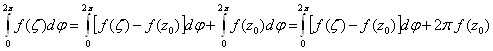(23)
Устремим теперь Вак нулю. Так как Ва- аналитическая, а следовательно, непрерывная функция в области , то для любого положительного числа 
Ваможно указать такое значение , что 
Вадля 
. Отсюда следует, что при 
Васуществует предел
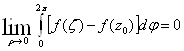
Так как в формуле (23) последнее слагаемое не зависит от Вато
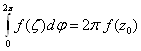, а следовательно 
Ваи согласно (22)
(24)
Интеграл, стоящий в правой части, выражает значение аналитической функции Вав некоторой точке Вачерез ее значения на любом контуре , лежащем в области аналитичности функции Ваи содержащем точку Вавнутри. Этот интеграл и называется интегралом Коши. Формула (24) часто называется формулой Коши.
Замечание 1. В формуле (24) интегрирование производится по замкнутому контуру , целиком лежащему в области аналитичности функции Ваи содержащему внутри точку . При дополнительном условии непрерывности Вав замкнутой области Вааналогичная формула имеет место в силу теоремы 6 (стр. 56) и при интегрировании по границе Ваобласти .
Замечание 2. Проведенные рассмотрения остаются справедливыми и в случае многосвязной области . При этом для вывода основной формулы (24) следует рассматривать такой замкнутый контур , который может быть стянут к точке , все время оставаясь в области . Тогда легко показать, что при условии непрерывности функции Вав замкнутой области Вас кусочно-гладкой границей формула (24) остается справедливой при интегрировании в положительном направлении по полной границе Ваданной многосвязной области.
Сделаем ряд замечаний по поводу формулы (24).
1. Интеграл вида 
Вапо замкнутому контуру Вацеликом лежащему в области Вааналитичности функции , имеет смысл для любого положения точки Вана комплексной плоскости при условии, что эта точка не лежит на контуре . При этом, если точка Валежит внутри , то значение интеграла равно 
; если точка Валежит вне , значение интеграла равно нулю, поскольку в этом случае подынтегральная функция является аналитической всюду внутри . Итак,
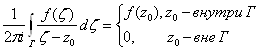(25)
При 
Ваинтеграл 
в обычном смысле не существует, однако при дополнительных требованиях на поведение функции Вана контуре Ваэтому интегралу может быть придан определенный смысл. Так, если функция Ваудовлетворяет на контуре Ваусловию Гёльдера*
то существует главное значение по Коши интеграла 
где 
Вапредставляет собой часть контура , лежащего вне круга 
. При этом
2. Пусть Ва- аналитическая функция в односвязной области Ваи Ва- некоторая внутренняя точка этой области. Опишем из этой точки как из центра окружность радиуса 
, целиком лежащую в области . Тогда по формуле Коши получим
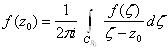
Но на окружности 
, поэтому
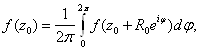(26)
Или
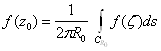Ва(27)
Эта формула носит название формулы среднего значения и выражает значение аналитической функции в центре окружности как среднее из ее граничных значений.
3. Принцип максимума модуля аналитической функции. Пусть функция Ваявляется аналитической в области Ваи непрерывной в замкнутой области . Тогда или 
, или максимальные значения 
Вадостигаются только на границе области.
Действительная функция двух действительных переменных
по условию является непрерывной в замкнутой области
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы