Математичнi методи представлення знань
МРЖНРЖСТЕРСТВО ОСВРЖТИ РЖ НАУКИ УКРАРЗНИ
Нацiональний унiверситет тАЬЛьвiвська полiтехнiкатАЭ
РЖнститут КомптАЩютерних наук та iнформацiйних технологiй
Кафедра автоматизованих систем управлiння
Лабораторна робота № 5-6
з дисциплiни
тАЬМатематичнi методи представлення знаньтАЭ
на тему:
ВлОбчислення означених iнтегралiвВ»
Виконав:
студент групи КН-29
Коцуба О.
Прийняв:
Биненко Б. РЖ.
Львiв тАУ 2011
Обчислення означених iнтегралiв
Мета роботи: вивчити методи наближених обчислень i запрограмувати алгоритми обчислення означених iнтегралiв .
Порядок роботи:
1. Попереднi опрацювання теоретичного матерiалу.
2. Отримання допуску до виконання лабораторноi роботи.
3. Опрацювання типового навчального завдання (прикладiв).
4. Створення проекту для виконання iндивiдуального завдання.
5. Оформити звiт для захисту лабораторноi роботи за зразком:
В· назва роботи;
В· мета роботи;
В· порядок роботи;
В· короткi теоретичнi вiдомостi;
В· алгоритм розвтАЩязування задачi;
В· тексти вiдповiдних модулiв проекту;
В· аналiз отриманих результатiв та висновки.
6. Захист лабораторноi роботи.
Короткi теоретичнi вiдомостi
1. Формули прямокутникiв.
Нехай на вiдрiзку
задана неперервна функцiя 
. Потрiбно обчислити iнтеграл 
РозiбтАЩiмо вiдрiзок Вана n рiвних частин точками 
, i=0,1,тАжn-1, довжина кожноi з яких дорiвнюi 
Ва. Через 
Вапозначимо значення функцii 
Вав точках 
Ваi складемо суми
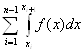Ваабо 
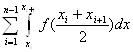
Кожна з цих сум i iнтегральною сумою для Вана вiдрiзку i тому наближено виражають означений iнтеграл:
Ва(1)
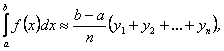Ва(1/)
Цi формули називаються формулами прямокутникiв. РЖз рис. 1 видно, що якщо 
додатна i зростаюча функцiя, то формула (1) вiдображаi площу ступiнчатоi фiгури, що складена iз тАЬ внутрiшнiхтАЭ прямокутникiв, а формула (1/) тАУ площу фiгури, що складена iз тАЬзовнiшнiхтАЭ прямокутникiв.
Похибка методу прямокутникiв даiться формулою (2):
Ва(2)
формула прямокутник лагранж функцiя
Похибка при цьому буде тим меншою, чим бiльше число n (тобто чим менший крок подiлу). Зауважимо, що формули прямокутникiв дають точнi результати для багаточленiв першого степеня.
2. Формула трапецiй.
Очевидно, що можна отримати бiльш точне значення iнтеграла, якщо дану криву Вазамiнити не ступiнчатою лiнiiю, як це мало мiсце у формулi прямокутникiв, а вписаною ламаною (рис.2). Тодi площа криволiнiйноi трапецii, обмеженоi лiнiями 
Ваi Вазамiниться площами трапецiй, обмежених зверху хордами Оскiльки площа
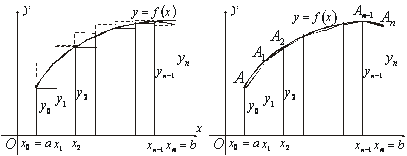
Рис.1 Рис.2
першоi трапецii дорiвнюi 
другоi тАУ 
Ваi т.д.,
то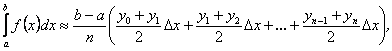 
або
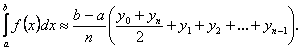Ва(3)
Формула (3) називаiться формулою трапецiй. Число n вибираiться довiльним, але чим бiльшим це число буде, а значить, крок Ваменшим, тим з бiльшою точнiстю сума в правiй частинi наближеноi рiвностi (3) буде давати значення iнтегралу.
3. Формула парабол (Сiмпсона).
Метод Сiмпсона найпоширенiший i простiше застосовний для програмування. Його суть полягаi в наближеннi пiдiнтегральноi функцii вiдрiзками парабол.
Отже, розглянемо спочатку iнтеграл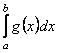 
, де 
ВатАУ парабола; 
,
,
тАУ деякi параметри (або числа).
Тодi
Нехай тепер маiмо iнтеграл 
, де 
Ва- неперервна на iнтервалi функцiя. Якщо iнтервал розбити на п рiвних частинок , i=0,1,тАжn-1,, то заданий iнтеграл РЖ можна записати так:
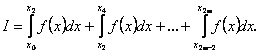
Якщо на кожному з iнтегралiв для промiжкiв 
Вафункцiю замiнимо параболами 
, що проходять через точки 
Ва,то одержимо
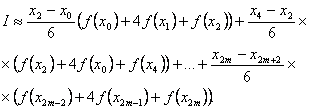
Через те, що, формула матиме вигляд:
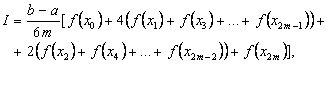Ваабо
Ва(4)
Формула (4) називаiться формулою парабол або Сiмпсона. Доведено, що похибка обчислень 
Ваза формулою Сiмпсона i такою:
Ва(5)
Проте, цiiю оцiнкою похибки можна користуватись, якщо Ваi хоча б чотири рази диференцiйовною. Але, якщо Ванавiть чотири рази диференцiйовна, то часто оцiнка четвертоi похiдноi 
Ваможе виявитись досить складною. Тому на практицi переважно користуються таким методом: обчислюють iнтеграл, роздiляючи iнтервал, заданий границями iнтегрування, один раз на n рiвних частин, а другий раз на т частин. Якщо одержанi двоi значень iнтеграла мало вiдрiзняються, то результат можна вважати прийнятним. Порiвнюючи iх можна оцiнити i точнiсть обчислень.
Приклад. Обчислити з точнiстю до 0,001 iнтеграл
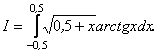
Р о з в тАЩ я з у в а н н я. За формулою (4) маiмо:
при Вапри
| 
| 
| | |
|
| |
|
|
| -0,5 | 0,0000 |
| -0,5 | 0,00000 | 
| 0,05 | 0,0371 |
| -0,4 | -0,1203 |
| -0,45 | -0,0946 | 
| 0,10 | 0,0772 |
| -0,3 | -0,1303 |
| -0,40 | -0,1203 |
| 0,15 | 0,1200 |
| -0,2 | -0,1081 |
| -0,35 | -0,1304 |
| 0,20 | 0,1652 |
| -0,1 | -0,630 |
| -0,30 | -0,1303 |
| 0,25 | 0,2122 |
| 0 | 0,0000 |
| -0,25 | -0,1204 |
| 0,30 | 0,2607 |
| 0,1 | 0,0772 |
| -0,20 | -0,1081 |
| 0,35 | 0,3103 |
| 0,2 | 0,1652 |
| -0,15 | -0,0881 |
| 0,40 | 0,3610 |
| 0,3 | 0,2607 |
| -0,10 | -0,0630 |
| 0,45 | 0,4121 |
| 0,4 | 0,36098 |
| -0,05 | -0,0335 | 
| 0,50 | 0,4637 |
| 0,5 | 0,46365 |
| 0,00 | 0,0000 | | | |
Отже,
.
Нехай деяка функцiя f(x) задана в вузлах iнтерполяцii:
Ва(i=1,2,3.,n) на вiдрiзку [а,b] таблицею значень: 
.ВаВаВаВаВаВаВаВа
Потрiбно знайти значення iнтегралу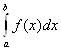 
.
Спершу складемо iнтерполяцiйний багаточлен Лагранжа:
Для рiвновiддалених вузлiв iнтерполяцiйний багаточлен маi вигляд:
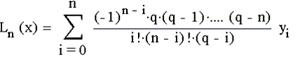
де q=(x-x0) /h тАУ крок iнтерполяцii, замiнимо пiдiнтегральну функцiю f(x) iнтерполяцiйним багаточленом Лагранжа:
Помiняiмо знак пiдсумовування i iнтеграл i винесемо за знак iнтеграла постiйнi елементи:
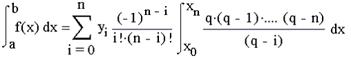
Оскiльки dp=dx/h, то, замiнивши межi iнтеграцii, маiмо:
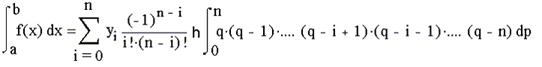
Для рiвновiддалених вузлiв iнтерполяцii на вiдрiзку [а,b] величина крок визначаiться як h=(b-a)/n. Представивши цей вираз для h у формулу (4) i виносячи (b-a) за знак суми, отримаiмо:
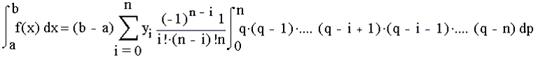
Покладемо, що
де i=0,1,2.,n; Числа 
Ваназивають коефiцiiнтами Ньютона-Kотеса. Цi коефiцiiнти не залежать вiд вигляду f(x), а i функцiiю тiльки по n. Тому iх можна обчислити заздалегiдь. Остаточна формула виглядаi так:
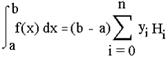
Формула трьох восьмих:
Якщо в формулi Ньютона-Котеса взяти n = 3, тобто функцiю f(x) замiнити iнтерполяцiйним багаточленом третього степеня, побудованим за значення функцii f(x) у точках x0=a, x1=a+h, x2=a+2h, x3=b, h=(b-a )/3. то одержимо таку квадратурну формулу:
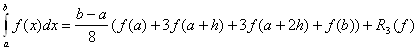Ваде
Ця квадратурна формула називаiться малою квадратурною формулою трьох восьмих. Використовуючи цю формулу, легко записати велику квадратурну формулу трьох восьмих.
Завдання
Обчислити iнтеграл методом прямокутникiв, трапецiй, парабол, трьох восьмих, Монте-Карло оцiнити абсолютну та вiдносну похибку обчислення :
А) заданий iнтеграл обчислити наближено та точно.
B) заданий iнтеграл обчислити наближено.
Варiант 1
1. 
2. 
3. 
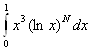
Варiант 2
1. 
2. 
3. 
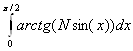
Варiант 3
1. 
2. 
3. 
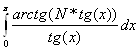
Варiант 4
1. 
2. 
3. 
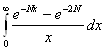
Варiант 5
1. 
2. 
3. 
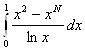
Варiант 6
1. 
2. 
3. 
Варiант 7
1. 
2. 
3. 
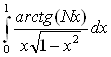
Варiант 8
1. 
2. 
3. 
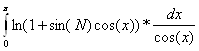
Варiант 9
1. 
2. 
3. 
Варiант 10
1. 
2. 
3. 
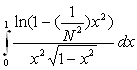
Рекомендована лiтература:
1. Цегелик Г.Г. Чисельнi методи: Пiдручник. тАУ Львiв: Видавничий центр ЛНУ iм. РЖ. Франка, 2004. тАУ 408 с.
2. Коссак О., Тумашова О., Коссак О. Методи наближених обчислень: Навч. посiб. тАУ Львiв: Бак, 2003. тАУ 168 с.
3. Анджейчак РЖ.А., Федю РД.М., Анохiн В.РД. i iн. Практикум з обчислювальноi математики. Основнi числовi методи. Частина РЖ. тАУ Навч. посiб. Львiв: Вид-во ДУ ВлЛьвiвська полiтехнiкаВ», 2000. тАУ 100 с.
4. Дудикевич А.Т., Левицька С.М., Шахно С.М. Практична реалiзацiя методiв розвтАЩязування нелiнiйних рiвнянь i систем: Навч.-метод. посiбн. тАУ Львiв: ВЦ ЛНУ iм. РЖ.Франка, 2007. тАУ 78 с.
5. Паранчук Я.С. та iн. Алгоритмiзацiя, програмування, числовi та символьнi обчислення в пакетi MathCAD. тАУ Навч. посiб. / Я.С. Паранчук, А.В. Маляр, Р.Я. Паранчук, РЖ.Р. Головач. тАУ Львiв: Вид-во Львiвськоi полiтехнiки, 2008. тАУ 164 с.
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы