Тривимiрнi перетворення

Вступ

Для кращого сприйняття форми об'iкта необхiдно мати його зображення в тривимiрному просторi. У багатьох випадках наочне представлення про об'iкт можна одержати шляхом виконання операцiй обертання i переносу, а також побудови проекцiй. Введемо однорiднi координати. Точка в тривимiрному просторi Вазадаiться чотиримiрним вектором Вачи . Перетворення з однорiдних координат описуiться спiввiдношеннями

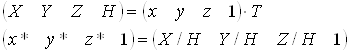(4.1)

де T - деяка матриця перетворення.

Ця матриця може бути представлена у виглядi 4 окремих частин

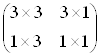
Матриця 3x3 здiйснюi лiнiйне перетворення у видi змiни масштабу, зсуву й обертання. Матриця-рядок 1х3 робить перенос, а матриця-стовпець 3х1 - перетворення в перспективi. Останнiй скалярний елемент виконуi загальну змiну масштабу. Повне перетворення, отримане шляхом впливу на вектор положення матрицею 4x4 i нормалiзацii перетвореного вектора, будемо називати бiлiнiйним перетворенням. Воно забезпечуi виконання комплексу операцiй зсуву, частковоi змiни масштабу, обертання, вiдображення, переносу, а також змiни масштабу зображення в цiлому.

Тривимiрна змiна масштабу

Дiагональнi елементи основноi матрицi перетворення 4х4 здiйснюють часткову i повну змiну масштабу. Розглянемо перетворення

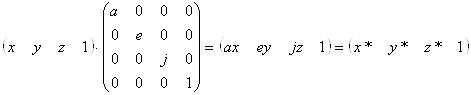,(4.2)

яке робить часткову змiну масштабу. На рис.4.1а показане перетворення паралелепiпеда в одиничний куб шляхом змiни масштабу. Загальна змiна масштабу виходить за рахунок використання четвертого дiагонального елемента, тобто

.ВаВаВаВаВаВаВаВаВа (4.3)

Це перетворення iлюструi рис.4.1б. Такий же результат можна отримати при рiвних коефiцiiнтах часткових змiн масштабiв. У цьому випадку матриця перетворення повинна бути рiвна

.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.4)

Вектори положення точок А i В рiвнi Ваi .

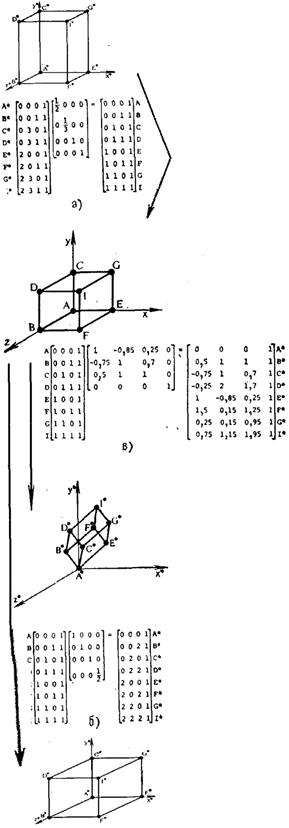
Рис.4.1. Тривимiрнi перетворення iз змiною масштабiв.

Тривимiрний зсув

Недiагональнi елементи верхньоi лiвоi пiдматрицi 3х3 вiд загальноi матрицi перетворення розмiру 4х4 здiйснюють зсуви в трьох вимiрах, тобто

.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4.5)

Простий тривимiрний зсув одиничного куба показаний на рис.4.1в.

Тривимiрнi обертання

Ранiше було показано, що матриця 3х3 забезпечувала комбiнацiю операцiй змiни масштабу i зсуву. Однак, якщо визначник матрицi 3х3 дорiвнюi +1, то маi мiсце чисте обертання навколо початку координат. Перед розглядом загального випадку тривимiрного обертання навколо довiльноi осi дослiдимо кiлька окремих випадкiв. При обертаннi навколо осi х розмiри уздовж осi х не змiнюються. Таким чином, матриця перетворень буде мати нулi в першому рядку i першому стовпцi, за винятком одиницi на головнiй дiагоналi. Це приводить до матрицi перетворення, що вiдповiдаi повороту на кут Ванавколо осi х i задаiться спiввiдношенням

(4.6)

Обертання вважаiться додатнiм, тобто за годинниковою стрiлкою, якщо дивитися з початку координат вздовж осi обертання. На рис.4.2а показаний поворот на -90В° навколо осi x.

Для обертання на кут Ф навколо осi y - нулi ставлять у другому рядку i другому стовпцi матрицi перетворення, за винятком одиницi на головнiй дiагоналi. Повна матриця задаiться виразом

(4.7)

Рис.4.2. Тривимiрнi обертання.

На рис.4.2б показаний поворот на 90В° навколо осi y. Аналогiчно матриця перетворення для обертання на кут Ванавколо осi z маi вид

(4.8)

Аналiз визначникiв для матриць (4.6)-(4.8) показуi, що для будь-якоi матрицi обертання детермiнант дорiвнюi +1.

Тому що обертання описуються множенням матриць, то тривимiрнi обертання некомутативнi, тобто порядок множення буде впливати на кiнцевий результат. Для того щоб показати це, розглянемо обертання навколо осi х, за яким слiдуi обертання на такий же кут навколо осi y. Використовуючи рiвняння (4.6) i (4.7) при = Ф, одержимо

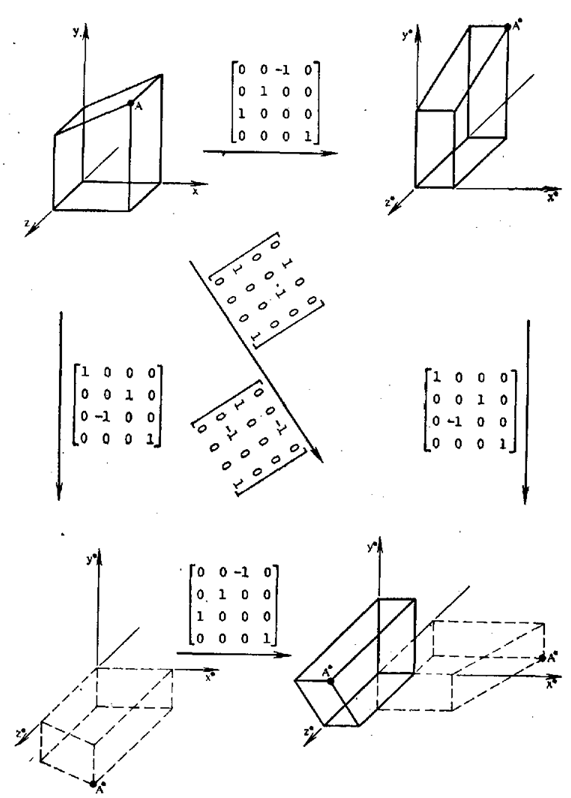
Рис.4.3. Некомутативнiсть тривимiрних обертань.

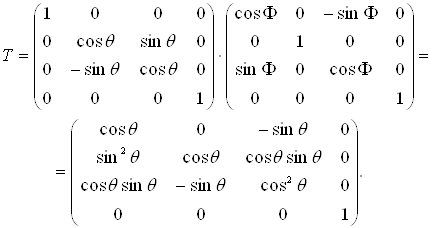(4.9)

Зворотна послiдовнiсть дiй, тобто обертання навколо осi y i наступне за ним обертання на такий же кут навколо осi x при = Ф даi

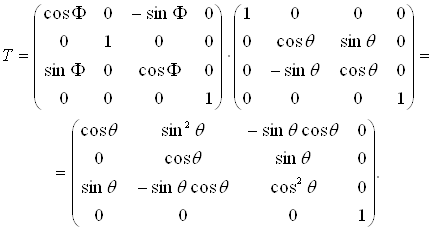(4.10)

На рис.4.3 для лiвого верхнього зображення штриховими лiнiями показанi результати двох послiдовних обертань, описаних матрицею перетворення (4.9). Зображення, отримане обертаннями, виконаними в iншiй послiдовностi, описаними рiвняннями (4.10), показанi суцiльною лiнiiю. З порiвняння отриманих зображень видно, що при змiнi порядку обертання виходять рiзнi результати.

Часто буваi необхiдно обертати зображення навколо однiii з осей декартовоi системи координат.

Вiдображення в просторi

РЖнодi потрiбно виконати дзеркальне вiдображення тривимiрного зображення. У трьох вимiрах найпростiше вiдображення здiйснюiться щодо площини. Для вiдображення без змiни масштабiв необхiдно, щоб визначник перетворення дорiвнював -1,0. При вiдображеннi щодо площини xy змiнюiться тiльки знак координати z. Отже, матриця перетворення для вiдображення щодо площини xy маi вигляд

(4.11)

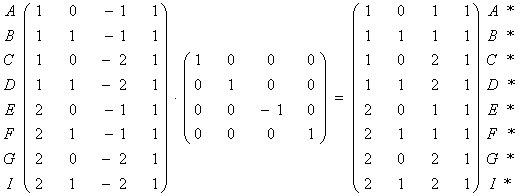
Вiдображення одиничного куба щодо площини ху показане на рис.4.4. Для вiдображення щодо площини уz

(4.12)

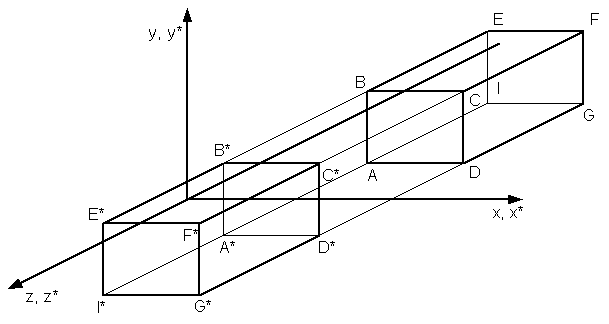
Рис.4.4. Просторове вiдображення щодо площини xy.

(4.12)

а для вiдображення щодо площини xz

(4.13)

Вiдображення щодо iнших площин можна одержати шляхом комбiнацii обертання i вiдображення.

Просторовий перенос

Тривимiрний лiнiйний перенос зображення задаiться виразом

(4.14)

Пiсля перемножування одержимо

(4.15)

Тривимiрне обертання навколо довiльноi осi

тривимiрне обертання фiгура вiдображення

Метод двовимiрного плоского обертання навколо довiльноi осi був розглянений ранiше. Узагальненням цього методу i спосiб обертання навколо довiльноi осi в тривимiрному просторi. Як i для плоского випадку, розглянена процедура полягаi в переносi зображення i заданоi осi обертання, що забезпечуi обертання навколо осi, що проходить через початок координат. Метод тривимiрного обертання полягаi в лiнiйному переносi, обертаннi навколо початку координат i зворотньому лiнiйному переносi у вихiдне положення. Якщо вiсь, навколо якоi виконуiться обертання, проходить через точку А = , то матриця перетворення визначаiться наступним виразом:

(4.16)

де елементи матрицi обертання R розмiру 4х4 визначаються в загальному випадку спiввiдношенням

(4.17)

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы