Симплексний метод лiнiйного програмування
Завдання 1
Кондитерська фабрика для виробництва трьох видiв карамелi А1, А2, А3 використовуi три види сировини: цукор-пiсок, патоку i фруктове пюре. Норми використання сировини кожного виду на виробництво однiii тони карамелi подано в таблицi, вiдома також загальна кiлькiсть сировини кожного виду i прибуток вiд реалiзацii 1 тонни карамелi певного виду.
| Вид сировини | Норми витрат сировини (т) на 1 т карамелi | ОбтАЩiм сировини, т |
А1 | А2 | А3 |
| Цукор-пiсок | 0,8 | 0,5 | 0,6 | 1000 |
| Патока | 0,4 | 0,4 | 0,3 | 800 |
| Фруктове пюре | - | 0,1 | 0,1 | 150 |
| Прибуток вiд реалiзацii 1 т продукцii (грн. од.) | 21 | 23 | 25 | |
РозвтАЩязок
Складаiмо математичну модель задачi. Позначимо через х1 кiлькiсть карамелi 1-го виду, що виготовляi пiдприiмство за деяким планом, а через х2 кiлькiсть карамелi 2-го виду та через х3 кiлькiсть карамелi 3-го виду. Тодi прибуток, отриманий пiдприiмством вiд реалiзацii цих виробiв, складаi
∫ = 21х1+23х2+25х3.
Витрати сировини на виготовлення такоi кiлькостi виробiв складають вiдповiдно:
CI =0,8х1+0,5х2+0,6х3,
CIРЖ =0,4х1+0,4х2+0,3х3,
CIРЖРЖ =0х1+0,1х2+0,1х3.
Оскiльки запаси сировини обмеженi, то повиннi виконуватись нерiвностi:
0,8х1+0,5х2+0,6х3≤1000
0,4х1+0,4х2+0,3х3≤800
0х1+0,1х2+0,1х3≤150.
Оскiльки, кiлькiсть виробiв i величина невiд'iмна, то додатково повиннi виконуватись ще нерiвностi: х1> 0, х2> 0, х3>0.
Таким чином, приходимо до математичноi моделi:
Знайти х1, х2, х3 такi, що функцiя ∫ = 21х1+23х2+25х3 досягаi максимуму при системi обмежень:
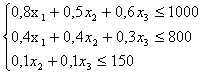
Розв'язуiмо задачу лiнiйного програмування симплексним методом.
Для побудови першого опорного плану систему нерiвностей приведемо до системи рiвнянь шляхом введення додаткових змiнних.
0,8x1 + 0,5x2 + 0,6x3 + 1x4 + 0x5 + 0x6 = 1000
0,4x1 + 0,4x2 + 0,3x3 + 0x4 + 1x5 + 0x6 = 800
0x1 + 0,1x2 + 0,1x3 + 0x4 + 0x5 + 1x6 = 150
де х1,..,х6>0
Матриця коефiцiiнтiв A = a(ij) цiii системи рiвнянь маi вигляд:
Базиснi змiннi це змiннi, якi входять лише в одне рiвняння системи обмежень i притому з одиничним коефiцiiнтом.
Вирiшимо систему рiвнянь вiдносно базисних змiнних:
x4 , x5 , x6
Вважаючи, що вiльнi змiннi рiвнi 0, отримаiмо перший опорний план:
X1 = (0,0,0,1000,800,150)
Оскiльки завдання вирiшуiться на максимум, то ведучий стовпець вибираiмо по максимальному негативному кiлькiстю та iндексного рядку. Всi перетворення проводимо до тих пiр, поки не вийдуть в iндексному рядку позитивнi елементи.
Складаiмо симплекс-таблицю:
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 1 | x4 | 1000 | 0.8 | 0.5 | 0.6 | 1 | 0 | 0 | 1666.67 |
| x5 | 800 | 0.4 | 0.4 | 0.3 | 0 | 1 | 0 | 2666.67 |
| x6 | 150 | 0 | 0.1 | 0.1 | 0 | 0 | 1 | 1500 |
| РЖндексний рядок | F(X1) | 0 | -21 | -23 | -25 | 0 | 0 | 0 | 0 |
Оскiльки, в iндексному рядку знаходяться негативнi коефiцiiнти, поточний опорний план неоптимальний, тому будуiмо новий план. У якостi ведучого виберемо елемент у стовбцi х3, оскiльки значення коефiцiiнта за модулем найбiльше.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 2 | x4 | 100 | 0.8 | -0.1 | 0 | 1 | 0 | -6 | 125 |
| x5 | 350 | 0.4 | 0.1 | 0 | 0 | 1 | -3 | 875 |
| x3 | 1500 | 0 | 1 | 1 | 0 | 0 | 10 | 0 |
| РЖндексний рядок | F(X2) | 37500 | -21 | 2 | 0 | 0 | 0 | 250 | 0 |
Даний план, також не оптимальний, тому будуiмо знову нову симплексну таблицю. У якостi ведучого виберемо елемент у стовбцi х1.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 3 | x1 | 125 | 1 | -0.13 | 0 | 1.25 | 0 | -7.5 | 0 |
| x5 | 300 | 0 | 0.15 | 0 | -0.5 | 1 | 0 | 2000 |
| x3 | 1500 | 0 | 1 | 1 | 0 | 0 | 10 | 1500 |
| РЖндексний рядок | F(X3) | 40125 | 0 | -0.63 | 0 | 26.25 | 0 | 92.5 | 0 |
Оскiльки, в iндексному рядку знаходяться негативнi коефiцiiнти, поточний опорний план неоптимальний, тому будуiмо новий план. У якостi ведучого виберемо елемент у стовбцi х2, оскiльки значення коефiцiiнта за модулем найбiльше.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 4 | x1 | 312.5 | 1 | 0 | 0.13 | 1.25 | 0 | -6.25 | 0 |
| x5 | 75 | 0 | 0 | -0.15 | -0.5 | 1 | -1.5 | 2000 |
| x2 | 1500 | 0 | 1 | 1 | 0 | 0 | 10 | 1500 |
| РЖндексний рядок | F(X4) | 41062.5 | 0 | 0 | 0.63 | 26.25 | 0 | 98.75 | 0 |
Оскiльки всi оцiнки >0, то знайдено оптимальний план, що забезпечуi максимальний прибуток: х1=312.5, х2=1500. Прибуток, при випуску продукцii за цим планом, становить 41062,5 грн.
Завдання 2
Записати двоiсту задачу до поставленоi задачi лiнiйного програмування. РозвтАЩязати одну iз задач симплексним методом i визначити оптимальний план iншоi задачi. Оптимальнi результати перевiрити графiчно.
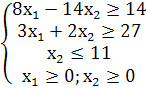
РозвтАЩязок
РозвтАЩяжемо задачу лiнiйного програмування симплексним методом.
Визначимо мiнiмальне значення цiльовоi функцii F(X)=5x1+3x2 при наступних умовах-обмежень.
8x1-14x2≥14
3x1+2x2≥27
x2≤11
Для побудови першого опорного плану систему нерiвностей приведемо до системи рiвнянь шляхом введення додаткових змiнних.
8x1-14x2-1x3 + 0x4 + 0x5 = 14
3x1 + 2x2 + 0x3-1x4 + 0x5 = 27
0x1 + 1x2 + 0x3 + 0x4 + 1x5 = 11
Введемо штучнi змiннi x.
8x1-14x2-1x3 + 0x4 + 0x5 + 1x6 + 0x7 = 14
3x1 + 2x2 + 0x3-1x4 + 0x5 + 0x6 + 1x7 = 27
0x1 + 1x2 + 0x3 + 0x4 + 1x5 + 0x6 + 0x7 = 11
Для постановки задачi на мiнiмум цiльову функцiю запишемо так:
F(X) = 5x1+3x2+Mx6+Mx7 => min
Вважаючи, що вiльнi змiннi рiвнi 0, отримаiмо перший опорний план:
X1 = (0,0,0,0,11,14,27)
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | х6 | х7 |
| 0 | х6 | 14 | 8 | -14 | -1 | 0 | 0 | 1 | 0 |
| x7 | 27 | 3 | 2 | 0 | -1 | 0 | 0 | 1 |
| х5 | 11 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| РЖндексний рядок | F(X0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Переходимо до основного алгоритму симплекс-методу.