Застосування симетричних многочленiв
Сумський держаний педагогiчний унiверситет iменi А. С. Макаренка
Кафедра математики
КУРСОВА РОБОТА
з алгебри
на тему: ВлЗАСТОСУВАННЯ СИМЕТРИЧНИХ МНОГОЧЛЕНРЖВВ»
Студенки 3 курсу 432 групи
напряму пiдготовки 0402 фiзико-математичних наук
спецiальностi 6.040203 математика
Рудченко Олени Володимирiвни
Керiвник викладач кафедри математики
Друшляк Марина Григорiвна
м. Суми тАУ 2010 р.
ЗМРЖСТ
ВСТУП
РОЗДРЖЛ I. ТЕОРЕТИЧНРЖ ПОЛОЖЕННЯ ПРО СИМЕТРИЧНРЖ МНОГОЧЛЕНИ ТА РЗХ ВЛАСТИВОСТРЖ
1.1 Загальнi поняття про симетричний многочлен
1.2 Властивостi симетричних многочленiв
РОЗДРЖЛ IРЖ. ЗАСТОСУВАННЯ СИМЕТРИЧНИХ МНОГОЧЛЕНРЖВ
2.1 РозвтАЩязування систем рiвнянь
2.2 Доведення тотожностей
2.3 Звiльнення вiд iррацiональностiВаВаВаВаВаВа
2.4 Вилучення коренiв
ВИСНОВКИ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
Важливе мiсце в курсi алгебри посiдають симетричнi многочлени та, зокрема, застосування симетричних многочленiв при розвтАЩязуваннi рiвнянь, систем рiвнянь, вилучення коренiв, доведення тотожностей, звiльнення вiд iррацiональностi у дробах тощо. Цими питаннями займалися багато вчених, зокрема, Франсуа Вiiт.
Франсуа Вiiт розробив ряд важливих питань теорii рiвнянь 1 тАФ 4 степенiв. Вiн сформулював i довiв кiлька теорем про взаiмозв'язки мiж коренями i коефiцiiнтами рiвнянь, зокрема, й теорему про зведене квадратне рiвняння (теорема Вiiта). На сьогоднiшнiй день теорема Вiiта i необхiдною i важливою частиною шкiльноi програми.
Дана курсова робота складаiться з вступу, двох роздiлiв, висновкiв i списку використаних джерел. Перший роздiл ВлТеоретичнi положення про симетричнi многочлени та iх властивостiВ» складаiться з двох параграфiв. Вони присвяченi загальним поняттям та основним властивостям симетричних многочленiв. Другий роздiл ВлЗастосування симетричних многочленiвВ» мiстить в собi приклади застосування симетричних многочленiв на практицi. Роздiл складаiться з чотирьох параграфiв. Вони присвяченi застосування симетричних многочленiв до розвтАЩязуваннi систем рiвнянь, доведення тотожностей, звiльнення вiд iррацiональностi у дробах та вилучення коренiв.
властивiсть рiвняння симетричний многочлен
РОЗДРЖЛ I. ТЕОРЕТИЧНРЖ ПОЛОЖЕННЯ ПРО СИМЕТРИЧНРЖ
МНОГОЧЛЕНИ ТА РЗХ ВЛАСТИВОСТРЖ
1.1 Загальнi поняття про симетричний многочлен
Серед найбiльш важких завдань на розвтАЩязання систем рiвнянь вищих степенiв i наступнi:
![]()
![]()
![]()
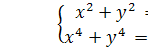
Усi цi системи мають одну загальну властивiсть - лiвi частини рiвнянь i многочленами, у якi x i y входять однаковим способом.
Означення.Многочлен вiд x i y називають симетричним, якщо вiн не змiнюiться при замiнi x на y, та y на x.
Означення.Симетричний многочлен тАФ многочлен вiд n змiнних F(x1, x2, тАж, xn), що не змiнюiться при всiх перестановках змiнних. Тобто многочлен F i R [x1, x2, тАж, xn] вiд n змiнних над комутативним кiльцем R i симетричним якщо для довiльноi перестановки.
![]()
Справедлива рiвнiсть: F(x1, x2, тАж, xn)
Симетричнi многочлени утворюють пiдалгебру R-алгебри R [x1, x2, тАж, xn] многочленiв вiд n змiнних над кiльцем R.
Многочлен x2y + xy2 - симетричний. Навпаки, многочлен x3 - 3y2 не i симетричним: при замiнi x на y, а y на x вiн перетворюiться на многочлен y3 - 3x2, який не збiгаiться з первинним.
Приведемо найважливiшi приклади симетричних многочленiв. Як вiдомо з арифметики, сума двох чисел не мiняiться при перестановцi доданкiв, тобто:
x + y = y + x
для будь-яких чисел x i y. Ця рiвнiсть показуi, що многочлен x + y i симетричним. Так само iз закону комутативностi множення xy = yx
витiкаi, що добуток xy i симетричним многочленом. Симетричнi многочлени x + y i xy i найпростiшими. РЗх називають елементарними симетричними многочленами вiд x i y. Для них використовують спецiальнi позначення:
![]()
Кожен многочлен вiд основних симетричних, i симетричним.
Окрiм ![]() i
i![]() , часто зустрiчаються так званi степеневi суми, тобто многочлени x2 + y2, x3 + y3, . . ., xn + yn, . . . Прийнято означати многочлен xn + yn через sn. Таким чином,
, часто зустрiчаються так званi степеневi суми, тобто многочлени x2 + y2, x3 + y3, . . ., xn + yn, . . . Прийнято означати многочлен xn + yn через sn. Таким чином,
![]()
![]()
![]()
![]()
![]() . (1)
. (1)
Ця формула дозволяi послiдовно знаходити Sn через ![]() i
i![]() . Так за допомогою цiii формули можна послiдовно знайти:
. Так за допомогою цiii формули можна послiдовно знайти:
![]()
 ;
;
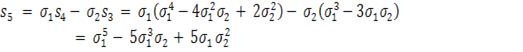
i т . д. У таблицi 1 зведенi вирази степеневих сум s1, s2, . . ., s10 через i цi вирази будуть нам кориснi при розвтАЩязаннi задач.
Таблиця 1 Вираження степеневих сум sn = xn + yn через ![]()
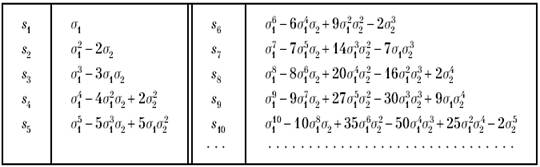
1.2 Властивостi симетричних многочленiв
Встановимо тепер деякi елементарнi властивостi довiльних симетричних многочленiв.
1. Сума, рiзниця i добуток симетричних многочленiв над деяким полем Р i симетричними многочленами над цим полем.
Це твердження очевидне.
Наслiдок.
Множина всiх симетричних многочленiв над полем Р утворюi область цiлiсностi з одиницею вiдносно дiй додавання i множення. ВаЗрозумiло, що це кiльце i пiдкiльцем всiх многочленiв над полем Р.
2. Якщо симетричний многочлен f (x1, x2, тАж, xn) мiстить деякий член
![]() Ва(2)
Ва(2)
то вiн мiстить i член, утворений з (2) внаслiдок будь-якоi перестановки показникiв ![]() .
.
Доведення. Оскiльки, як вiдомо, вiд довiльноi перестановки показникiв![]() до всякоi iншоi перестановки цих показникiв можна перейти за допомогою скiнченного числа транспозицiй, то досить показати, що при транспозицii довiльних двох показникiв степенiв у членi (2) ми дiстаiмо знову деякий член симетричного многочлена
до всякоi iншоi перестановки цих показникiв можна перейти за допомогою скiнченного числа транспозицiй, то досить показати, що при транспозицii довiльних двох показникiв степенiв у членi (2) ми дiстаiмо знову деякий член симетричного многочлена
f (x1, x2, тАж, xn)
Виконуючи, наприклад, транспозицiю показникiв , ![]() та
та ![]() , матимемо член
, матимемо член
![]() Ва(3)
Ва(3)
За означенням симетричного многочлена
f (![]() ,
, ![]() , тАж,
, тАж,![]() xn) = f (
xn) = f (![]() ,
, ![]() , тАж,
, тАж,![]() xn)
xn)
Але другий з цих многочленiв повинен мiстити член (3), бо його дiстаiмо з члена (2) замiною ![]() на
на ![]() i навпаки. Тому внаслiдок iдиностi канонiчноi форми i даний многочлен повинен мiстити член (3).
i навпаки. Тому внаслiдок iдиностi канонiчноi форми i даний многочлен повинен мiстити член (3).
Наслiдок. Якщо
![]() Ва(4)
Ва(4)
i вищий член симетричного многочлена, то ![]() .
.
Доведення.Справдi, припустимо супротивне, тобто що при якомусь ![]() . На пiдставi властивостi 2 даний многочлен разом з членом (4) мiстить i член
. На пiдставi властивостi 2 даний многочлен разом з членом (4) мiстить i член
![]() Ва(5)
Ва(5)
Але з умови ![]() Вавипливаi, що член (5) вищий за член (4), тобто член (4) не може бути вищим у многочленi. Ця суперечнiсть доводить наше твердження.
Вавипливаi, що член (5) вищий за член (4), тобто член (4) не може бути вищим у многочленi. Ця суперечнiсть доводить наше твердження.
Також можна сформулювати таку важливу властивiсть симетричних многочленiв, яку називають основною теоремою.
Теорема1 (Основна теорема теорii симетричних многочленiв): Всякий симетричний многочлен f (x1, x2, тАж, xn) вiд п змiнних над полем Р можна подати у виглядi многочлена вiд основних симетричних функцiй ![]() цих змiнних, коефiцiiнти якого належать тому самому полю Р. РЖ таке зображення iдине.
цих змiнних, коефiцiiнти якого належать тому самому полю Р. РЖ таке зображення iдине.
Доведення. Зробимо насамперед такi зауваження.
1) Усiх членiв певного степеня L, утворених з даних змiнних x1, x2, тАж, xn (не враховуючи подiбних), може бути лише скiнченне число; це число, очевидно, дорiвнюi числу способiв, якими можна подати як суму n невiд'iмних цiлих упорядкованих доданкiв.
2) Теорему досить довести для однорiдних симетричних многочленiв, бо всякий симетричний многочлен можна подати як суму однорiдних симетричних многочленiв. Справдi, всякий многочлен i сумою однорiдних многочленiв. Якщо ж даний многочлен симетричний, то й кожний складовий однорiдний многочлен повинен бути симетричний, бо при переставляннi змiнних x1, x2, тАж, xn кожний член може перейти лише в член того самого степеня, тобто в iнший член того самого однорiдного складового многочлена.
3) Вищий член ![]() Вабудь-якого симетричного многочлена можна подати як вищий член деякого добутку основних симетричних функцiй
Вабудь-якого симетричного многочлена можна подати як вищий член деякого добутку основних симетричних функцiй ![]()
Справдi, розглянемо добуток
![]() (6)
(6)
За наслiдком з властивостi 2, всi степенi ![]()
![]() тАФ невiд'iмнi числа, тому (6) i многочленом вiд x1, x2, тАж, xn. За лемою, вищий член цього многочлена дорiвнюi добутку вищих членiв многочленiв
тАФ невiд'iмнi числа, тому (6) i многочленом вiд x1, x2, тАж, xn. За лемою, вищий член цього многочлена дорiвнюi добутку вищих членiв многочленiв ![]() Ва(причому пiднесення до степеня слiд розглядати як множення однакових многочленiв). Оскiльки вищi члени
Ва(причому пiднесення до степеня слiд розглядати як множення однакових многочленiв). Оскiльки вищi члени![]() дорiвнюють вiдповiдно x1; x1x2;тАж; x1x2тАж xn-1; x1x2тАж xn-1xn, то вищий член добутку (6) дорiвнюi:
дорiвнюють вiдповiдно x1; x1x2;тАж; x1x2тАж xn-1; x1x2тАж xn-1xn, то вищий член добутку (6) дорiвнюi:
![]()
тобто (як це видно пiсля елементарних перетворень) збiгаiться з заданим членом ![]()
Пiсля цих зауважень легко довести теорему.
1) Доведення РЖснування. Нехай вищий член симетричного многочлена f (x1, x2, тАж, xn)(який ми в результатi зауваження 2 можемо вважати однорiдним многочленом степеня N) дорiвнюi
![]() (7)
(7)
Побудуiмо симетричний многочлен
![]()
Згiдно з зауваженням 3, вищий член цього многочлена дорiвнюi (7). Крiм того, вiн однорiдний, бо такими i всi многочлени ![]() , а тому, очевидно, i iх добуток. Степiнь многочлена
, а тому, очевидно, i iх добуток. Степiнь многочлена ![]() дорiвнюi степеню многочлена f (x1, x2, тАж, xn)бо в них однаковi вищi члени.
дорiвнюi степеню многочлена f (x1, x2, тАж, xn)бо в них однаковi вищi члени.
Вiзьмемо
f1(![]() ,
, ![]() , тАж
, тАж![]() xn)
xn) ![]() f (
f (![]() ,
, ![]() ,
,![]() xn) -
xn) - ![]() Ва.
Ва.
Зрозумiло, що f (![]() ,
, ![]() ,
,![]() xn) тАФ також однорiдний симетричний многочлен степеня N. Але
xn) тАФ також однорiдний симетричний многочлен степеня N. Але ![]() (
(![]() ,
, ![]() ,
,![]() xn) вже не мiстить усiх членiв цього степеня. Справдi, вiн не мiстить вищого члена (7), який у цiй рiзницi знищуiться. Крiм того, в цiй рiзницi знищуються всi n! членiв, якi дiстаiмо з вищого члена перестановкою показникiв
xn) вже не мiстить усiх членiв цього степеня. Справдi, вiн не мiстить вищого члена (7), який у цiй рiзницi знищуiться. Крiм того, в цiй рiзницi знищуються всi n! членiв, якi дiстаiмо з вищого члена перестановкою показникiв ![]() Вабо цi члени, за властивiстю 2, входять в обидва симетричнi многочлени.
Вабо цi члени, за властивiстю 2, входять в обидва симетричнi многочлени.
Тепер зрозумiло, що ![]() (
(![]() ,
, ![]() ,
,![]() xn) може мiстити лише члени, нижчi за (7). Застосовуiмо до цього многочлена той самий метод. Нехай вищий член многочлена маi вигляд:
xn) може мiстити лише члени, нижчi за (7). Застосовуiмо до цього многочлена той самий метод. Нехай вищий член многочлена маi вигляд:
![]() (8)
(8)
Вважаючи
![]() ВаB
ВаB![]()
i утворюючи рiзницю:
f2(![]() ,
, ![]() , тАж
, тАж![]() xn)
xn) ![]() f1(
f1(![]() ,
, ![]() ,
,![]() xn) -
xn) - ![]() ,
,
бачимо, що ![]() (
(![]() ,
, ![]() ,
,![]() xn) i симетричний i однорiдний многочлен степеня N, який не може мiстити нi члена (7), нi члена (8), а тiльки члени, нижчi за них. Оскiльки, взагалi, рiзних членiв степеня N може бути лише скiнченне число (зауваження 1), то, продовжуючи цей процес, ми на якомусь кроцi обов'язково дiстанемо, що рiзниця
xn) i симетричний i однорiдний многочлен степеня N, який не може мiстити нi члена (7), нi члена (8), а тiльки члени, нижчi за них. Оскiльки, взагалi, рiзних членiв степеня N може бути лише скiнченне число (зауваження 1), то, продовжуючи цей процес, ми на якомусь кроцi обов'язково дiстанемо, що рiзниця
fk+1 (x1, x2, тАжxп) = fk (x1, x2, тАжxп) - gk(x1, x2, тАжxn)
не може мiстити жодного члена степеня N, тобто дорiвнюi нулю. Тодi з рiвностей
![]() ,
,
![]() ,
,
.
![]()
випливаi, що
![]() .
.
А оскiльки всi ![]() Вавираженi через
Вавираженi через ![]() Вадобутки то многочлен f(
Вадобутки то многочлен f(![]() ,
, ![]() ,
,![]() xn)подано як многочлен вiд основних симетричних функцiй f(
xn)подано як многочлен вiд основних симетричних функцiй f(![]() ,
, ![]() ,
,![]() xn) =
xn) = ![]() (9)
(9)
коефiцiiнти якого знайдено з коефiцiiнтiв даного многочлена за допомогою операцiй додавання i вiднiмання i тому належать полю Р. Теорему доведено. Справедлива також теорема про i д.и н i с т ь многочлена ![]()
2) Доведення iдиностi.
Нехай маiмо
f(![]() ,
, ![]() ,
,![]() xn) =
xn) = ![]()
f(![]() ,
, ![]() ,
,![]() xn) =
xn) = ![]()
Тодi рiзниця
![]() Ва=
Ва= ![]()
повинна дорiвнювати нулю при будь-яких значеннях x1, x2, тАж, xn.
Зауважимо, що многочлен ![]() Ваможна розглядати двояко:як многочлен вiд x1, x2, тАж, xn (бо вiд цих змiнних залежать
Ваможна розглядати двояко:як многочлен вiд x1, x2, тАж, xn (бо вiд цих змiнних залежать ![]() Ва) i як многочлен вiд
Ва) i як многочлен вiд ![]() нам треба розглянути останнi. РДдинiсть зображення (9) полягаi саме в тому, що многочлени,
нам треба розглянути останнi. РДдинiсть зображення (9) полягаi саме в тому, що многочлени, ![]() Вамають однаковi вiдповiднi коефiцiiнти, тобто що многочлен
Вамають однаковi вiдповiднi коефiцiiнти, тобто що многочлен ![]() Вамаi коефiцiiнти
Вамаi коефiцiiнти ![]() Ваякi дорiвнюють нулю, в усiх членах
Ваякi дорiвнюють нулю, в усiх членах ![]() . Але
. Але ![]() Вазалежнi мiж собою, бо виражаються через тi самi змiннi
Вазалежнi мiж собою, бо виражаються через тi самi змiннi ![]() ,
, ![]() ,
,![]() xn. У зв'язку з цим поряд з многочленом
xn. У зв'язку з цим поряд з многочленом ![]() Вавiд залежних змiнних розглянемо такий самий многочлен
Вавiд залежних змiнних розглянемо такий самий многочлен ![]() Вавiд незалежних змiнних
Вавiд незалежних змiнних ![]() . Тепер нам треба довести, що коли
. Тепер нам треба довести, що коли ![]() Ватой
Ватой ![]() . Те саме можна сформулювати й iнакше: нам треба довести, що коли
. Те саме можна сформулювати й iнакше: нам треба довести, що коли ![]() , то тодi й
, то тодi й ![]() Ва.
Ва.
Доведемо це методом математичноi iндукцii по n. Нехай n=1 i ![]() . Через те, що
. Через те, що ![]() Вав цьому разi дорiвнюi x1, то
Вав цьому разi дорiвнюi x1, то ![]() , бо
, бо ![]() , що те саме, що й
, що те саме, що й
Нехай тепер п > 1, i наше твердження правильне для будь-якого числа змiнних, меншого п. Чи може бути воно несправедливим для якогось многочлена вiд п змiнних? Припустимо, що це так i iснуi многочлен ![]() такий, що
такий, що ![]() , але
, але ![]() . Подамо
. Подамо ![]() за степенями yп
за степенями yп
![]()
![]()
де ![]() ВатАФ многочлени вiд
ВатАФ многочлени вiд ![]() , за нашим припущенням
, за нашим припущенням
![]()
![]() (11)
(11)
Оскiльки ![]() Ва, то хоч би один з його коефiцiiнтiв в (10) не дорiвнюi нулю. Завжди можна вважати, що
Ва, то хоч би один з його коефiцiiнтiв в (10) не дорiвнюi нулю. Завжди можна вважати, що ![]() . Якщо
. Якщо ![]() Ва, то надалi мiркування проводять вiдносно многочлена
Ва, то надалi мiркування проводять вiдносно многочлена ![]() , який дiстаiмо з
, який дiстаiмо з ![]() Вапiсля скорочення на. Виходить, що при уп = 0
Вапiсля скорочення на. Виходить, що при уп = 0
![]() (12)
(12)
З другого боку, вiзьмемо в (11) хп = 0. Тодi ![]() , а iншi
, а iншi ![]() , перетворюються в основнi симетричнi функцii вiд (п-1) змiнних. Позначимо iх через
, перетворюються в основнi симетричнi функцii вiд (п-1) змiнних. Позначимо iх через ![]() .Отже, при хп = 0 з (11) дiстаiмо:
.Отже, при хп = 0 з (11) дiстаiмо:
![]() , 0) =
, 0) = ![]() Ва(13)
Ва(13)
Порiвнюючи (12) з (13) бачимо, що ми прийшли до суперечностi з припущенням iндукцii, а тому висловлене твердження справедливе i для п.
РДдинiсть зображення (9) доведено.
З основноi теореми теорii симетричних многочленiв можна зробити важливий висновок.
Теорема 2: Якщо f(x) тАФ многочлен вiд однiii змiнноi над полем Р з коренями ![]() (якi можуть не належати Р), то будь-який симетричний многочлен f (x1, x2, тАж, xn) над полем Р при
(якi можуть не належати Р), то будь-який симетричний многочлен f (x1, x2, тАж, xn) над полем Р при ![]() Ванабуваi значення, яке i елементом поля Р.
Ванабуваi значення, яке i елементом поля Р.
Доведення. Нехай дано якийсь многочлен n-го степеня вiд одного змiнного (в зведеному виглядi) над полем Р:
![]() (14)
(14)
Позначимо коренi цього многочлена через ![]() ; вони можуть i не належати полю Р. Вiзьмемо тепер довiльний симетричний многочлен
; вони можуть i не належати полю Р. Вiзьмемо тепер довiльний симетричний многочлен ![]() над Р вiд п змiнних. За основною теоремою теорii симетричних многочленiв, многочлен
над Р вiд п змiнних. За основною теоремою теорii симетричних многочленiв, многочлен ![]() можна подати у виглядi многочлена вiд основних симетричних функцiй
можна подати у виглядi многочлена вiд основних симетричних функцiй ![]() Ваз коефiцiiнтами з поля Р, тобто
Ваз коефiцiiнтами з поля Р, тобто ![]()
Вiзьмемо тепер тут ![]() . Тодi за формулами Вiiта всi основнi симетричнi функцii дорiвнюватимуть вiдповiдним коефiцiiнтам многочлена (14) з належним знаком:
. Тодi за формулами Вiiта всi основнi симетричнi функцii дорiвнюватимуть вiдповiдним коефiцiiнтам многочлена (14) з належним знаком:
![]()
![]()
тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж
![]()
У зв'язку з цим
![]()
Але тодi ![]() Ваелемент поля Р як результат ви конання операцiй додавання i множення над елементами з поля Р. Таким чином,
Ваелемент поля Р як результат ви конання операцiй додавання i множення над елементами з поля Р. Таким чином, ![]() . Отже, ми довели таке твердження.
. Отже, ми довели таке твердження.
У рядi питань доводиться зустрiчатися з задачею побудови за даним многочленом f(х) iР [х]з коренями ![]() Ватакого многочлена g(у), коренi якого
Ватакого многочлена g(у), коренi якого ![]() виражаються через вiдповiднi коренi
виражаються через вiдповiднi коренi ![]() за допомогою деякого многочлена у = f(х)над полем Р;
за допомогою деякого многочлена у = f(х)над полем Р; ![]() . Найпростiшi задачi такого типу зустрiчаються в шкiльному курсi алгебри для Р = Q. Оскiльки коефiцiiнти
. Найпростiшi задачi такого типу зустрiчаються в шкiльному курсi алгебри для Р = Q. Оскiльки коефiцiiнти ![]() многочлена g(у)вiдповiдно до формул Вiiта визначаються рiвностями
многочлена g(у)вiдповiдно до формул Вiiта визначаються рiвностями
![]()
![]()
тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАжтАж
![]() ,
,
то вони i значеннями деяких симетричних многочленiв над Р, аргументи яких i коренями даного многочлена f(х). З oсновноi теореми теорii симетричних многочленiв випливаi, що завжди можна знайти вираз коефiцiiнтiв ![]() через коефiцieнти даного многочлена, а з теореми 3 зрозумiло, що знайдений многочлен належатиме тому самому кiльцю Р [х], що й даний многочлен.
через коефiцieнти даного многочлена, а з теореми 3 зрозумiло, що знайдений многочлен належатиме тому самому кiльцю Р [х], що й даний многочлен.
Зауважимо, що сказане залишаiться справедливим i для бiльш загального випадку, коли ![]() ,де
,де ![]() - довiльнi симетричнi многочлени над полем Р.
- довiльнi симетричнi многочлени над полем Р.
Розглянутий вище метод доведення основноi теореми можна використати для практичного зображення симетричних многочленiв через основнi симетричнi функцii.
Приклад. Подати симетричний многочлен над полем
![]() Ва+
Ва+
+ ![]()
через основнi симетричнi функцii. Як i при доведеннi теореми, запишемо цей многочлен як суму однорiдних многочленiв. Дiстанемо:
![]()
де ![]()
![]()
Спочатку ![]() Ваподамо через основнi симетричнi многочлени. Вищий його член i
Ваподамо через основнi симетричнi многочлени. Вищий його член i ![]() . Згiдно з методикою доведення теореми, вiд
. Згiдно з методикою доведення теореми, вiд ![]() слiд вiдняти многочлен
слiд вiдняти многочлен
![]()
бо система показникiв у вищому членi i 2, 1, 0. Але немаi потреби фактично виконувати це вiднiмання. Спираючись на можливiсть i iдинiсть зображення даного многочлена у виглядi многочлена ![]() досить визначити можливий вигляд членiв
досить визначити можливий вигляд членiв ![]() Ваi скористатися методом невизначених коефiцiiнтiв.
Ваi скористатися методом невизначених коефiцiiнтiв.
У рiзницi ![]() знищаться всi члени виду
знищаться всi члени виду ![]() Ваздовiльною перестановкою показникiв 2, 1, 0. Проте одночасно можуть з'явитися члени того самого степеня 3, але з iншою, нижчою системою показникiв, а саме: 1, 1, 1. Отже, потiм треба буде вiдняти симетричний многочлен
Ваздовiльною перестановкою показникiв 2, 1, 0. Проте одночасно можуть з'явитися члени того самого степеня 3, але з iншою, нижчою системою показникiв, а саме: 1, 1, 1. Отже, потiм треба буде вiдняти симетричний многочлен
![]()
Тому можна записати: ![]() ,
,
де а тАФ невизначений поки що коефiцiiнт, тобто:
![]()
![]()
Щоб знайти а, досить надати деяких числових значень змiнним![]() наприклад
наприклад ![]() Ва= 1.Тодi дiстанемо 6 = 9 + а. Отже, а =
Ва= 1.Тодi дiстанемо 6 = 9 + а. Отже, а = ![]() 3. Таким чином,
3. Таким чином,
![]()
Аналогiчно мiркуватимемо вiдносно многочлена
![]()
Можливi системи показникiв тут будуть 2, 0, 0 i 1, 1, 0. Отже, вiднiматимемо такi многочлени:
![]()
![]()
РЖ далi, аналогiчно до попереднього, ![]() . При
. При ![]() Ва= 1 маiмо 3 = 32 + b
Ва= 1 маiмо 3 = 32 + b ![]() Ва3, тобто b =
Ва3, тобто b = ![]() 2 i тому
2 i тому
![]() (15)
(15)
Отже, дiстаiмо остаточно ![]()
РОЗДРЖЛ IРЖ. ЗАСТОСУВАННЯ СИМЕТРИЧНИХ
МНОГОЧЛЕНРЖВ
2.1 РозвтАЩязування систем рiвнянь
Дуже часто зустрiчаються системи рiвнянь, лiвi частини яких симетрично залежать вiд невiдомих x, y. В цьому випадку зручно перейти до нових невiдомих ![]() . За основною теоремою теорii симетричних многочленiв, це завжди можливо. Необхiднiсть такоi замiни невiдомих полягаi в тому, що степенi рiвнянь пiсля замiни зменшуються (оскiльки
. За основною теоремою теорii симетричних многочленiв, це завжди можливо. Необхiднiсть такоi замiни невiдомих полягаi в тому, що степенi рiвнянь пiсля замiни зменшуються (оскiльки ![]() Ваi многочленом другоi степенi вiд x, y). РЖншими словами, як правило, розвтАЩязування системи вiдносно нових невiдомих
Ваi многочленом другоi степенi вiд x, y). РЖншими словами, як правило, розвтАЩязування системи вiдносно нових невiдомих![]() простiше, нiж розвтАЩязування первинноi системи.
простiше, нiж розвтАЩязування первинноi системи.
Пiсля того, як знайденi значення величин ![]() Ва, треба знайти значення первинних невiдомих x, y. Це може бути зроблено за допомогою наступноi теореми
Ва, треба знайти значення первинних невiдомих x, y. Це може бути зроблено за допомогою наступноi теореми
Теорема. Нехай ![]() Ва- два довiльнi числа. Квадратне рiвняння
Ва- два довiльнi числа. Квадратне рiвняння
![]() (*)
(*)
i система рiвнянь
![]() (**)
(**)
пов'язанi один з одним таким чином: якщо z1, z2 тАУ корнi квадратного рiвняння (*), то система (**) маi два розвтАЩязки:
i iнших розвтАЩязкiв не маi; якщо x = a, y = b - розвтАЩязки системи (**), то числа a i b i коренями квадратного рiвняння (*).
Доведення. Якщо z1 i z2 тАУ корнi квадратного рiвняння (*), то по формулах Вiiта
![]()
![]()
тобто числа
i розвтАЩязками системи (**). Те, що iнших розвтАЩязкiв система (**) не маi, витiкаi з останнього твердження теореми, яке ми зараз доведемо.
Отже, нехай x = a, y = b - розвтАЩязок системи (**), тобто
![]()
ab =![]() .
.
Тодi ми маiмо
![]()
Але це означаi, що числа a i b являються коренями квадратного рiвняння (*). Теорема доведена.
Наведемо приклади.
Приклад 1.РозвтАЩязати систему рiвнянь
![]()
Введемо новi невiдомi ![]() Вазнаходимо:
Вазнаходимо:
![]()
а тому для нових невiдомих отримуiмо наступну систему рiвнянь:
![]()
З цiii системи рiвнянь отримуiмо ![]() .
.
Отже, ![]() Ватобто для первинних невiдомих x, y ми отримуiмо наступну систему рiвнянь :
Ватобто для первинних невiдомих x, y ми отримуiмо наступну систему рiвнянь :
![]()
Ця система рiвнянь легко розвтАЩязуiться, i ми отримуiмо наступний розвтАЩязок первинноi системи:
Приклад 2.РозвтАЩязати систему рiвнянь
![]()
РозвтАЩязання проводиться аналогiчно. Вважаючи, що ![]() Ваприводимо початкову систему до вигляду
Ваприводимо початкову систему до вигляду
![]()
Звiдси для ![]() Ваотримуiмо квадратне рiвняння
Ваотримуiмо квадратне рiвняння
![]()
Чи
![]()
З цього рiвняння знаходимо два значення для: ![]()
Таким чином, для первинних невiдомих x, y отримуiмо двi системи рiвнянь:
![]() Вата
Вата ![]() РозвтАЩязавши цi системи, знаходимо чотири розвтАЩязки первинноi системи:
РозвтАЩязавши цi системи, знаходимо чотири розвтАЩязки первинноi системи:
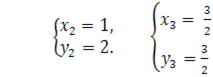
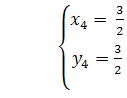
2.2 Доведення тотожностей
У цiлому рядi завдань на доведення тотожностi також з успiхом можуть бути застосованi елементарнi симетричнi многочлени. За основною теоремою симетричних многочленiв, кожну степеневу суму ![]() Ваможна представити у виглядi многочлена вiд,
Ваможна представити у виглядi многочлена вiд, ![]()
Таблиця 2. 1 Вирази степенних сум ![]() Вачерез,
Вачерез, ![]()

Кожну степеневу суму![]() можна представити у виглядi многочлена вiд
можна представити у виглядi многочлена вiд ![]() ,
, ![]() , за умови, що
, за умови, що ![]() .
.
Таблиця 2.2 Вирази степенних сум ![]() Вачерез
Вачерез ![]() Вапри виконаннi умови
Вапри виконаннi умови ![]()

РЖснують одночлени, якi не змiнюються при перестановцi змiнних тАУ симетричнi одночлени. Легко побачити, що усi змiннi в такий одночлен повиннi входити в одному i тому ж степенi, тобто цей одночлен повинен збiгатися з добутком Ва(взятий з деяким числовим коефiцiiнтом).
Якщо показники степеня одночлена i рiзними то цей одночлен не i симетричним. Щоб отримати симетричний одночлен, одним iз доданкiв, якого i, необхiдно додати до нього iншi одночлени.
Позначимо через O тАУ многочленз найменшим числом членiв, одним iз доданкiв, якого i одночлен, цей многочлен маi назву орбiта.
Для отримання орбiти одночлена необхiдно додати до нього одночлени отриманi за допомогою перестановок змiнних x, y, z. Якщо три показники степеня (k, l, m) не рiвнi мiж собою, то орбiта O(![]() буде складатися з шести членiв. Наприклад:
буде складатися з шести членiв. Наприклад:
О(![]()
Частинним випадком таких орбiт i степеневi суми:
O(![]()
Якщо k = l = m, то орбiта i одночленом:
О(![]() .
.
З цих формул за допомогою спiввiдношень
![]() (*)
(*)
Якщо k = l, то отримаiмо
![]() (**)
(**)
З цього легко отримати вирази орбiт O(xkyl) через ![]() за умови, що
за умови, що ![]()
У таблицi 2.3 наведенi вирази деяких орбiт O(xkyl) через ![]() ,
, ![]()
Таблиця 2.3 Вирази орбiт O(xkyl) через ![]()

Наприклад,
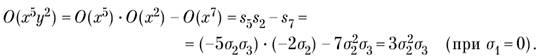
Приклад 1.Довести, що якщо x + y + z = 0, то
![]()
За таблицею 2.1 маiмо:
![]() .
.
За умовою s1 = x + y + z = 0, i тому ![]() .
.
Приклад 2. Довести, що якщо
x + y + z =![]() , то xyz = 0.
, то xyz = 0.
Умова завдання записуiться у виглядi
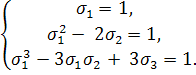
З цiii системи рiвностi знаходимо, що s2=0 i s3 = 0. Рiвнiсть s3=0 i означаi, що xyz=0.
Приклад 3. Довести, що якщо x + y + z = 0 i xy + xz + yz = 0, то справедлива рiвнiсть
![]()
З наведеноi таблицi 2.3, легко знаходимо (за умов ![]() Ва) :
Ва) :
![]()
крiм того, згiдно таблицi 2.2:
![]()
З цих спiввiдношень безпосередньо витiкаi доводжувана рiвнiсть.
Приклад 4. Довести, тотожнiсть
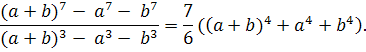
Для доведення позначимо число (тАУ a тАУ b) через c: с = тАУ a тАУ b.
Тодi a + b + c = 0 i можна застосувати формули, запропонованi у таблицi 2. 2. Лiва частина доводжуваноi тотожностi перетвориться таким чином:
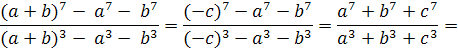
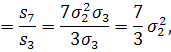
а права - таким чином:
![]()
![]()
Таким чином, доводжувана рiвнiсть справедлива.
Вказанi способи доведення тотожностi нерiдко застосовуються у поiднаннi з наступним прийомом: якщо обидвi частини, тiii тотожностi, що доводимо, виражаiться через рiзницi a![]() b, b
b, b![]() c, c
c, c![]() a, то зручно зробити замiну x = a
a, то зручно зробити замiну x = a![]() b, y = b
b, y = b![]() c, z = c
c, z = c![]() a, тодi x + +y + z = (a
a, тодi x + +y + z = (a![]() b)(b
b)(b![]() c)(c
c)(c![]() a) = 0 i тому можна застосовувати формули, запропонованi у таблицi 2. 2. Той же прийом можна застосовувати при розкладаннi на множники многочленiв, що виражаються через рiзницi a
a) = 0 i тому можна застосовувати формули, запропонованi у таблицi 2. 2. Той же прийом можна застосовувати при розкладаннi на множники многочленiв, що виражаються через рiзницi a![]() b, b
b, b![]() c, c
c, c![]() a.Розглянемо приклад.
a.Розглянемо приклад.
Приклад 5.Розкласти на множники многочлен
![]()
Вважаючи, що x = a![]() b, y = b
b, y = b![]() c, z = c
c, z = c![]() a, знаходимо:
a, знаходимо:
![]()
![]()
Ми скористались формулою ![]() Ва, запропонована у таблицi 2. 2.
Ва, запропонована у таблицi 2. 2.
2.3 Звiльнення вiд iррацiональностi
Симетричнi многочлени дозволяють розвтАЩязати багато важких завдань про звiльнення вiд iррацiональностi в знаменнику. У разi, коли знаменник маi вигляд ![]() Ваабо
Ваабо ![]() Вацю задачу можна вирiшити i без застосування симетричних многочленiв. Для цього досить використовувати формули
Вацю задачу можна вирiшити i без застосування симетричних многочленiв. Для цього досить використовувати формули
![]()
![]()
![]()
Складнiше йде справа, якщо знаменник складаiться з трьох або бiльшого числа iррацiональних доданкiв. Тут i можуть допомогти симетричнi многочлени. Розглянемо наступнi приклади.
Приклад 1. Звiльнитися вiд iррацiональностi в знаменнику виразу
![]()
Покладемо ![]() ВаТодi знаменник i не чим iншим, як елементаpним симетричним многочленом
ВаТодi знаменник i не чим iншим, як елементаpним симетричним многочленом ![]() Спробуiмо пiдшукати множник, пiсля множення на який знаменник вдасться виразити через статечнi суми s2 i s4. Оскiльки цi степеневi суми мають вигляд
Спробуiмо пiдшукати множник, пiсля множення на який знаменник вдасться виразити через статечнi суми s2 i s4. Оскiльки цi степеневi суми мають вигляд
![]()
![]()
знаменник стане рацiональним виразом. Для знаходження цього множника використовуiмо формули
![]()
![]()
(За табл. 2.1.). Ми бачимо, що в обох степеневих сумах лише останнiй доданок (у правiй частинi) не дiлиться на ![]() . Але дуже легко скомбiнувати цi степеневi суми так, щоб останнi доданки, що заважають нам, взаiмно знищилися. Для цього суму
. Але дуже легко скомбiнувати цi степеневi суми так, щоб останнi доданки, що заважають нам, взаiмно знищилися. Для цього суму ![]() Вапiднесемо до квадрату
Вапiднесемо до квадрату
![]()
i вiднiмемо з цього квадрата подвоiну суму ![]() . Ми отримаiмо:
. Ми отримаiмо:
![]() ,
,
Звiдки:
![]() )
)
Згадуючи, що ![]() ми знаходимо (використовуючи вказанi вище спiввiдношення
ми знаходимо (використовуючи вказанi вище спiввiдношення
![]()
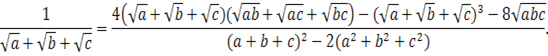
Залишаiться помножити обидвi частини отриманоi рiвностi на q .
Зауваження. Щоб уникнути дещо неприiмного (при розкриттi дужок в чисельнику) вираження, можна було б спочатку перетворити чисельник в правiй частинi формули (*). Використовуючи спiввiдношення
![]()
ми можемо переписати формулу (*) у виглядi
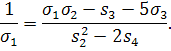
Звiдси ( вважаючи, як i ранiше, ![]() Ва) отримуiмо рiшення задачi в зручнiшому виглядi:
Ва) отримуiмо рiшення задачi в зручнiшому виглядi:
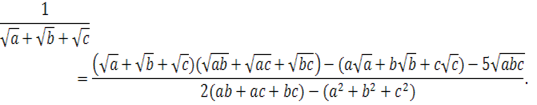
Приклад 2. Звiльнитися вiд iррацiональностi в знаменнику виразу
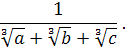
Напишемо вираз степеневоi суми s3 :
![]()
В правiй частинi тiльки останнiй доданок ![]() Ване дiлиться на
Ване дiлиться на ![]() Ва. Переносячи його в лiву частину, отримуiмо:
Ва. Переносячи його в лiву частину, отримуiмо:
![]() ,
,
Звiдки:
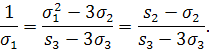
Поклавши ![]() Вазнаходимо:
Вазнаходимо:
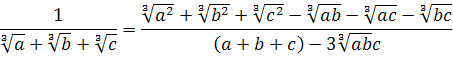
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы