Метод золотого перерiзу для пошуку екстремумiв функцiй

МРЖНРЖСТЕРСТВО ОСВРЖТИ РЖ НАУКИ УКРАРЗНИ

УЖГОРОДСЬКИЙ НАЦРЖОНАЛЬНИЙ УНРЖВЕРСИТЕТ

КАФЕДРА КОМПтАЩЮТЕРНИХ СИСТЕМ РЖ МЕРЕЖ

КУРСОВА РОБОТА

З курсу тАЬОбчислювальна технiка i програмуваннятАЭ

на тему: тАЬМетод золотого перерiзу для пошуку екстремумiв функцiйтАЭ

Ужгород 2009

Змiст

Вступ

1. Теоретичнi вiдомостi

1.1 Мiнiмiзацiя функцii однiii змiнноi

1.2 Метод золотого подiлу вiдрiзка

2. Постановка задачi

3. Текст програми

4. Результат роботи програми

Висновок

Список використаноi лiтератури

Вступ

Через 2500 рокiв пiсля стародавнiх грекiв в сучаснiй науцi на переднiй план знов вийшли три ВлвiчнiВ» проблеми (рахунки, вимiрювання i гармонii систем), якi стояли бiля витокiв створення математики i точних наук. Авторовi вдалося об'iднати новi математичнi теорii, данi для вирiшення цих проблем, в струнку математичну теорiю, названу ВлМатематикою ГармонiiВ». У основi цiй математики лежить ВлЗолотий ПеретинВ»! Ця нова математика може стати початком нового етапу в розвитку ВлВищоi МатематикиВ» i основою для створення новоi науки - ВлНауки про Гармонiю СистемВ». Вона може також стати початком реформи математичноi освiти i нових комп'ютерних проектiв, заснованих на Золотому Перетинi.

Ще однiiю тенденцiiю сучасних наукових дослiджень i повернення до проблемi гармонii систем , яка стояла в центрi античноi науки; у зв'язку з цим виникаi iнтерес до знаменитого ВлЗолотого ПеретинуВ», який зiграв в розвитку людськоi культури не меншу роль, чим число π, яке лежить в основi тригонометрii. РЖоганн Кеплер назвав Золотий Перетин одним з Влскарбiв геометрiiВ» i порiвняв його iз знаменитою ВлТеоремою ПiфагораВ». Оцiнюючи роль Золотого Перетину у розвитку старогрецькоi культури, генiальний росiйський фiлософ Олексiй Лосев якось сказав: ВлЗ погляду Платона, та i взагалi з погляду всiii античноi космологii, свiт i якесь пропорцiйне цiле, таке, що пiдкоряiться закону гармонiйного дiлення - Золотого ПеретинуВ».

РЖз Золотим Перетином тiсно пов'язано iнше математичне вiдкриття, зроблене в 13-му столiттi видатним iталiйським математиком Леонардо Пiзано (по прiзвиську Фiбоначчi).

Йдеться про так званi числа Фiбоначчi, якi пiзнiше були вибранi предметом математичного дослiдження групою американських математикiв, що органiзували в 1963 р. так звану Фiбоначчi-асоцiацiю. Золотий Перетин i пов'язанi з ними числа Фiбоначчi пронизуi всю iсторiю культури. Пiрамiда Хеопса, скульптурнi i архiтектурнi пам'ятники грецькоi культури i епохи Ренесансу, неперевершена ВлДжокондаВ» Леонардо да Вiнчi, картини Рафаеля Шишкiна i Костянтина Васильова, етюди Шопена, музика Бетховена, Чайковського i Белли Барток, ВлМодулорВ» КорбюзтАЩi, сосновi шишки, кактуси, ананаси, морськi зiрки i раковини, РДгипетський календар, квазiкристали Шехтмана - ось далеко не повний перелiк ВлтворiвВ» природи, науки i мистецтва, наповнених чудовою гармонiiю, в основi якоi лежить Золотий Перетин!

Золотий Перетин займаi значне мiсце в сучасних дослiдженнях кiлькiсних спiввiдношеннях живоi i неживоi природи. Яскравi вiдкриття сучасноi науки - квазiкристали Шехтмана, нова геометрична теорiя фiллотаксиса украiнського архiтектора Боднара, закон структурноi гармонii систем бiлоруського фiлософа Сороко, резонансна теорiя Сонячноi системи росiйського астронома Бутусова i iншi сучаснi науковi вiдкриття, заснованi на Золотому Перетинi, поза сумнiвом мають ВлстратегiчнеВ» значення для розвитку сучасноi науки. Необхiдно вiдзначити також великий iнтерес сучасноi теоретичноi фiзики золотому перетину. РЖншими словами, в даний час неможливо уявити собi подальший розвиток наук про природу без Золотого Перетину. РЖ i надiя, що i математична освiта також не залишиться в сторонi вiд Золотого Перетину.

1. Теоретичнi вiдомостi

З задачами пошуку екстремуму однiii змiнноi частково вивчають у курсi математичного аналiзу. На перший погляд цi задачi видаються простими i добре вивченими. Однак методи диференцiального числення мають обмежене застосування i не завжди зручнi для реалiзацii на ЕОМ. Хоча в останнi десятилiття зтАЩявилися набагато зручнiшi методи для використання на ЕОМ, якi вимагають меншого обтАЩiму чисельноi роботи, але тим не бiльше цю область екстремальних задач не можна рахувати завершеною. Роботи, присвяченi для нових методiв екстримiзацii однiii змiнноi, продовжують зтАЩявлятися на сторiнках математичних книг i журналiв. Ми тут зупинимося на декотрих найбiльш вiдомих методах, якi достатньо добре себе проявили на практицi.

1.1 Мiнiмiзацiя однiii змiнноi

Задача мiнiмiзацii однiii змiнноi маi такий вигляд: 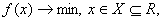Ваде

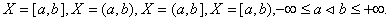
Залежно вiд функцii 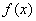Ваi множини 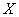Вамножина розвтАЩязкiв 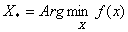, може мiстити одну, декiлька, або навiть i безмежну кiлькiсть точок. Можливi випадки, коли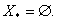

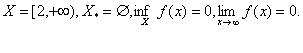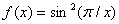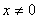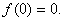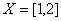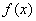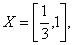Приклад 1: нехай , при Ваi ВаНа множинi Вамiнiмальне значення Вадорiвнюi 0, одна точка. Якщо то 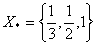- три точки, у випадку 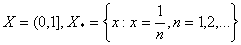Ва- зчисленна множина точок, а для

Зазначимо таке: якщо 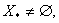Вато нижня межа i min функцii 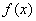Вазбiгаються 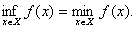У цьому випадку говорять,що 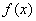Вана 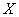Вадосягаi своii нижньоi межi,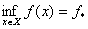завжди iснуi, а 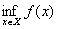Ване завжди маi сенс.

Означення I: Послiдовнiсть 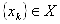називають мiнiмiзацiйною для функцii 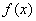на множинi 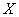, якщо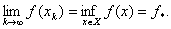

Означення II: Послiдовнiсть 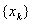збiгаiться до не порожньоi множини 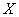, якщо 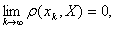Ваде 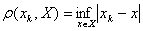Ва- вiдстань вiд 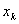до множини.

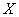Якщо 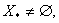Вато завжди iснуi мiнiмiзацiйна послiдовнiсть, яка збiгаiться до . Однак не кожна мiнiмiзацiйна послiдовнiсть 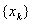буде збiгатися до .

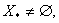Приклад 2:

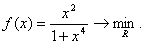
У нашому випадку 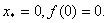ВаПослiдовнiсть 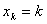Вадля 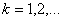i мiнiмiзацiйною

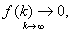
хоча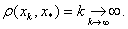

У разi розвтАЩязування задач мiнiмiзацii на множинi 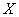Варозрiзнятимемо два типи задач:

1) Необхiдно визначити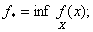

2) Потрiбно визначити 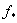Ваi точку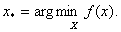

У першому випадку можливий варiант 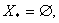Вау другому тАУ обовтАЩязково 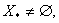. Отримати точний розвтАЩязок задачi першого,або другого типiв практично неможливо. Тому в першому випадку за 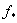Ваберуть, для мiнiмiзацiйноi послiдовностi 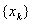, деяке значення 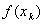Вапри достатньо великому . Для задач другого типу необхiдно побудувати мiнiмiзацiйну послiдовнiсть ,яка збiгаiться до , i за наближення до 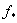Ваi 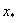Вавзяти, вiдповiдно 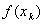Ваi 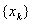при достатньо великому. Пiд час розвтАЩязування задач другого типу в окремих випадках треба виконувати додатковi дослiдження.

У випадку розвтАЩязування задачi можна використовувати класичний метод. Нехай функцiя 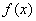Вакусковогладка на [a,b], тобто може iснувати лише скiнчена кiлькiсть точок, де 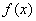Вамаi розрив першого роду, або неперервна, однак не маi похiдноi. У цьому разi точкою екстремуму функцii 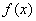на [a,b] може бути лише та точка, для якоi виконуiться одна з умов:

1). 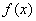Вамаi розрив першого роду;

2). 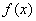Ванеперервна, однак похiдна не iснуi;

3).

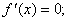
4). х тАУ точка на кiнцi вiдрiзка;

Цi точки прийнято називати пiдозрiлими на екстремум. На жаль, класичний метод маi досить вузьке застосування. Обчислення похiдноi 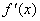Вав окремих випадках може бути трудомiсткими, або 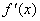Вавзагалi неможливо обчислити.

Крiм того, розвтАЩязування рiвняння 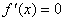Ваможе бути не менш складним, нiж вихiдна задача. Тому на практицi використовують методи, якi дають змогу безпосередньо знайти мiнiмум 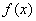. Для цього треба зробити обмеження на класи функцii.

Означення III. Функцiя 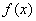Ваi унiмодальною на промiжку 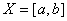, якщо iснують такi числа 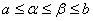, що:

1). 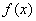строго монотонно спадаi при ;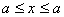

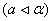2). 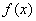строго монотонно зростаi при ;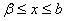

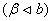3). 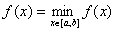Вапри , тобто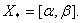

Випадки, коли один з вiдрiзкiв 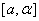, , 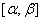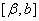Ваабо два одночасно вироджуються в точку, можливi. Якщ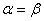о , то 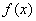Ваi строго унiмодальною на [a,b].

Означення IV. Вiдрiзок 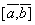Ваi локалiзований, якщо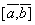 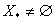Ваi значення 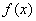Ваобчислено не бiльше, нiж в однiй точцi .

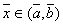1.2 Метод золотого подiлу вiдрiзку

Означення V. Золотим подiлом вiдрiзка на двi неоднаковi частини називають подiл, за якого вiдношення довжини всього вiдрiзка до довжини довшоi його частини дорiвнюi вiдношенню довжини довшоi частини вiдрiзка до довжини його коротшоi частини.

У випадку вiдрiзка одиничноi довжини 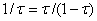, звiдси 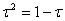Ваi .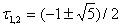

Отже, довший вiдрiзок маi довжину 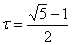, а коротший .

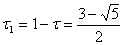У випадку довiльного вiдрiзку [a,b] точками золотого перерiзу i

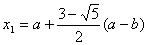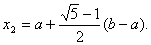, Ва(1)

Виявляiться, що точки х_1,х₂ тАУ це точки золотого подiлу для вiдрiзкiв вiдповiдно 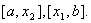ВаВикористовуючи властивiсть точок золотого подiлу, можна запропонувати для розвтАЩязування задачi (1.1) метод золотого подiлу вiдрiзка. Алгоритм цього методу такий.

Приймемо 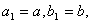Вавиберемо точки

золотий подiл вiдрiзок екстремум

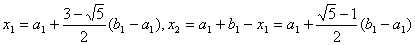
й обчислимо значення 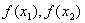. Якщо 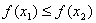, то приймемо 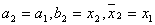, в iншому випадку 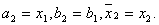Побудований вiдрiзок 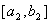Ваi локалiзований ,

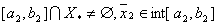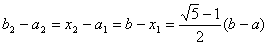
i вiдомо значення 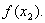ВаНехай уже визначено точки 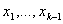, локалiзований вiдрiзок 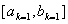, обчислено вiдповiднi значення функцii

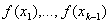.У цьому випадку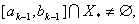

Вiдома точка 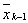, яка виконуi золотий перерiз вiдрiзка 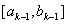, i обчислено значення мiнiмiзацiйноi функцii в цiй точцi: 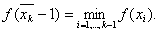ВаЗа iншу точку вибираiмо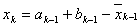 , яка i другою точкою золотого перерiзу вiдрiзка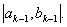

У цiй точцi обчислюiмо 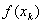Ваi визначаiмо локалiзований вiдрiзок 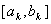, а саме (будемо вважати, що 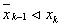) у випадку 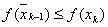Ваприймемо 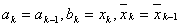, а у випадку 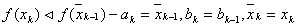Ва(випадок 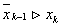Варозглядаiться аналогiчно). Новий вiдрiзок 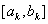Ваi локалiзований

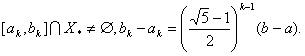
Точка 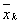Ва- це точка золотого подiлу вiдрiзка 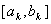i в цiй точцi обчислено значення функцii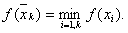Якщо кiлькiсть обчислень функцii 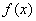Ване обмежено,то цей процес можна продовжити доти, доки не виконаiться нерiвнiсть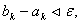 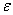Ва- задана точнiсть обчислень. Якщо кiлькiсть обчислень функцii задана i дорiвнюi , то пiсля отримання локалiзованого вiдрiзка 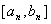обчислення припиняiмо i на розвтАЩязок задачi другого типу беремо 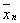- наближення до множини Ваз похибкою

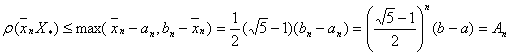
Якщо враховувати аналогiчну оцiнку в методi подiлу вiдрiзка наполовину

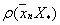
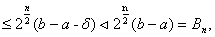
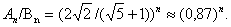
Отже, навiть для малих метод золотого подiлу ефективнiший, нiж метод подiлу вiдрiзка наполовину. Недолiком методу золотого подiлу в запропоновану виглядi i його нестiйкiсть. Розглянемо числову реалiзацii методу. ОбовтАЩязково число 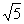Вабуде задано наближено, а це призведе до наближеного обчислення точок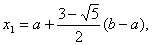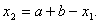ВаРозглянемо як ця похибка впливатиме на результат наступних крокiв. Уведемо позначення 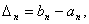Ватодi маiмо рiзницеве рiвняння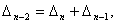 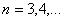з початковими умовами 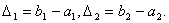(2)

РозвтАЩязок шукатимемо у виглядi 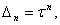Вадля визначення 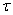Вамаiмо характеристичне рiвняння 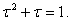(3)

Лiнiйно незалежними частинними розвтАЩязками рiвняння (2) будуть 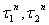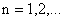Ва, де 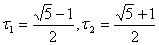Ва- коренi рiвняння (3). Довiльний розвтАЩязок (2) можна записати у виглядi

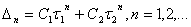(4)

Сталi С₁,С₂можна визначити з початкових умов

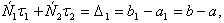
(5)

У разi точного розвтАЩязування системи (5)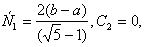

тодi 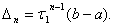Однак на практицi замiсть 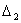Вау системi (5) беремо наближене значення 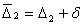Ваi замiсть (4) з точними значеннями С₁,С₂= 0 отримаiмо

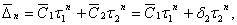
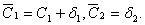
Оскiльки 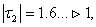Вато похибка становитиме

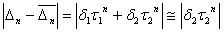
i зi збiльшенням зростатиме досить швидко. Отже, уже для малих точки 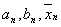Вавiдрiзнятимуться вiд теоретичних, якi можна отримати лише внаслiдок точних обчислень. Практичнi пiдрахунки також пiдтвердили нестiйкiсть методу. Цей недолiк можна легко усунути. Нехай маiмо локалiзований вiдрiзок 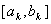i внутрiшню точку 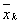iз обчисленим значенням 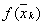. Знаходимо точки золотого подiлу вiдрiзка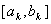

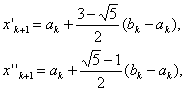
Точку, яка i далi вiд точки 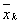Вавибираiмо за 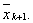В iншому алгоритм незмiнний. За такоi модифiкацii метод втрачаi симетричнiсть i красу в обчисленнi, однак зберiгаi стiйкiсть i повнiстю вiдповiдаi теоретичним висновкам.

2. Постановка задачi

Задача 1. Знайти Вадля заданоi функцii 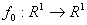Ваi заданого вiдрiзка .

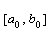Припущення 1. Функцiя 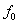Ватака, що на вiдрiзку 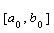точка ii локального мiнiмуму 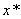Ваi точкою абсолютного мiнiмуму на вiдрiзку .

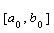Алгоритм 1

Початок. I. Обчислити константу 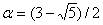Ва().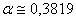

II. Обчислити точки

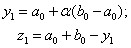
i значення .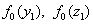

III. Якщо 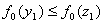, то покласти 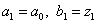Ваi перейти на крок IV, iнакше покласти 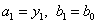Ваi перейти на крок IV.

IV. Покласти

Основний цикл. V. Якщо 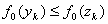, то обчислити 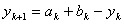, 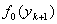Ваi перейти на крок VI; iнакше покласти 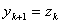, 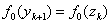Ваi перейти на крок VII.

VI. Покласти

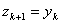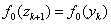
i перейти на крок VIII.

VII. Обчислити 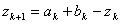, 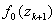Ваi перейти на крок VIII.

VIII. Якщо 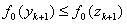, то покласти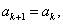 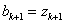Ваi перейти на крок IX; iнакше покласти 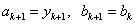Ваi перейти на крок IX.

IX. Обчислити .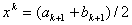

X. Покласти 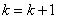Ваi перейти на крок V.

Теорема 1. Якщо виконуiться припущення 1, то послiдовнiсть 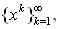Ваяка породжена алгоритмом 1, така, що

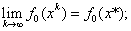
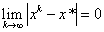Зауваження 1. Довжина вiдрiзку 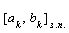, побудованого по методу золотого перерiзу, на 17% бiльша довжини вiдрiзку 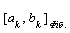, побудованого по методу Фiбоначi. Проте метод золотого перерiзу маi наступну перевагу, що на кожнiй його iтерацii доводиться робити менше обчислень.

Зауваження 1'. РЖнодi на практицi комбiнують обидва методи: першi кроки роблять по методу золотого перерiзу, а коли оптимум достатньо близький, обраховують число m i переходять до методу Фiбоначi.

3. Текст програми

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, Menus, TeEngine, Series, ExtCtrls, TeeProcs, Chart;

type

TForm1 = class(TForm)

Button1: TButton;

Edit1: TEdit;

Edit2: TEdit;

Edit3: TEdit;

Label1: TLabel;

Edit4: TEdit;

Label2: TLabel;

Label3: TLabel;

Label4: TLabel;

Memo1: TMemo;

Label5: TLabel;

Chart1: TChart;

Series1: TLineSeries;

procedure Button1Click(Sender: TObject);

procedure FormActivate(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

eps:real;

a,b,ao,bo:real;

alpha:real;

x1,x2:real;

f1,f2:real;

x_opt:real;

implementation

{$R *.dfm}

function f(x:real):extended;

begin

f:=sin(x+1); //zadannja potribnoji fynkchiji !!!

end;

procedure TForm1.FormActivate(Sender: TObject);

begin

Memo1.Lines.Clear;

Memo1.Lines.Add('F(x)= sin(x+1)');

end;

procedure TForm1.Button1Click(Sender: TObject);

var h:real;xx:real; i:integer;

begin

eps:=StrToFloat(Edit1.Text);

ao:=StrToFloat(Edit2.Text);

bo:=StrToFloat(Edit3.Text);

a:=ao; b:=bo;

alpha:=(sqrt(5)-1)/2;

x1:=bo-alpha*(bo-ao);

x2:=ao+alpha*(bo-ao);

f1:=f(x1);

f2:=f(x2);

while abs(a-b)>eps do

BEGIN

if f1>{<}f2 then

begin

b:=x2;

x2:=x1;

f2:=f1;

x1:=b-alpha*(b-a);

f1:=f(x1);

end ELSE

begin

a:=x1;

x1:=x2;

f1:=f2;

x2:=a+alpha*(b-a);

f2:=f(x2);

end;

END;

x_opt:=(a+b)/2;

Edit4.Text:=FloatToStr(x_opt);

{--------------------------------}

xx:=ao;

h:=(bo-ao)/20;

for i:=1 to 20 do

begin

Series1.AddXY(xx,f(xx),'',clblue);

xx:=xx+h;

end;

end.

4. Результат роботи програми

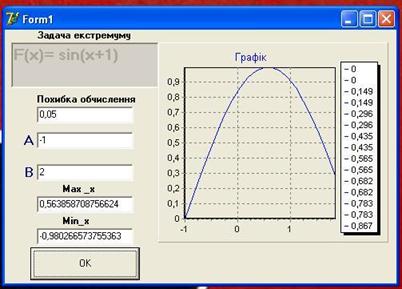
Рис. 1

РозвтАЩязок вручну:

РозвтАЩязок рiвняння в роботi РозвтАЩязок прикладу 2

Отже максимум = -1 при х = В±1, у = 4 тАУ т. мiнiмума

а мiнiмум = 0,57 при х = В±2, у =13 тАУ т. максимума

Висновок

Метод золотого перерiзу належить до симетричних методiв. Використовуючи цю iдею, можна будувати й iншi симетричнi методи, але як i в методi золотого подiлу, iх потрiбно дослiджувати на стiйкiсть.

Список використаноi лiтератури

1. Сторнгин Р.Г. Численные методы в многоэкстремальных задачах (Информационно-статистические алгоритмы). тАУ М.: Наука, 1978. тАУ240 с.

2. Бейко И.В., Бублик Б.Н., Зинько П.Н. Методы и алгоритмы решения задач оптимизации. тАУ К.: Вища школа, 1983. тАУ512 с.

3. ВаСтахов О.П. За принципом золотоi пропорцii: перспективний шлях розвитку обчислювальноi технiки. Журнал "Вiсник Академii наук Украiнськоi РСР", №1-2, 1990 г.

4. Ю.В. Васильков, Н.Н. Василькова. ВлКомпютерные технологии вычислений в математическом моделированиеВ» Москва, Влфинансы и статистикаВ» 2002. тАУ 249 с.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы