Вычисление электрической энергии и электрических сил

М.И. Векслер, Г.Г. Зегря

Полная энергия заряженной системы определяется как

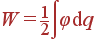
(24)

Она состоит из собственных энергий тел системы Wown, i и энергий взаимодействия каждого из тел со всеми остальными Wint, i, all. При необходимости можно разбить Wint, i, all на энергии попарного взаимодействия Wint, i, j. Для вычисления собственной энергии i-го тела при интегрировании учитывается только им создаваемый потенциал, а для нахождения Wint, i, all - напротив, потенциал всех тел, кроме i-го:

W	=		(25)
	=

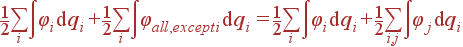
При наличии заряженных точек или нитей в местах их нахождения оказывается φ = ∞. Собственные энергии таких объектов и полная энергия - формально - равны ∞, так что рассмотрению подлежат лишь энергии взаимодействия.

В случае двух тел энергия их взаимодействия - это энергия взаимодействия первого тела со вторым Wint, 1, 2 плюс равная ей энергия взаимодействия второго тела с первым Wint, 2, 1:

(26)

Сила взаимодействия двух тел может быть найдена как сила, действующая со стороны первого тела на второе или (что - с точностью до знака - то же самое) как сила, с которой второе тело действует на первое:

(27)

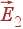Здесь - поле, создаваемое одним первым, а - одним вторым телом.

Задача. Шар R, равномерно заряженный по объему (ρ0). Найти собственную энергию заряженного шара.

Решение: Мы должны сначала найти потенциал внутри шара, для чего ищем по теореме Гаусса поле:

	=
	=

Это поле мы интегрируем, получая φ(r) для r

φ(r)	=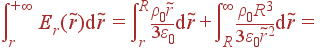

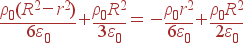
Имея потенциал и записав dq как

dq = ρ0 r2dr sinθdθ dφ

можно найти энергию шара непосредственным интегрированием:

Wown	=

Эта энергия совпадает с полной энергией, поскольку система состоит только из одного тела.

Задача. Точечный заряд q находится на расстоянии l от проводящей плоскости. Найти энергию и силу взаимодействия заряда со своим изображением.

Ответ: , , 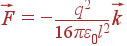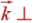плоскости.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы