Определение дуальных и двойных чисел
В настоящее время различные виды комплексных чисел изучаются довольно интенсивно. С учением о комплексных числах связаны важные, не решённые до сегодняшнего дня задачи, над которыми работают учёные во многих странах.
Все системы самых общих комплексных чисел фактически сводятся к следующим трём различным системам: обыкновенные комплексные числа, дуальные числа, двойные числа.
Обыкновенные комплексные числа тесно связаны с вопросом о решении уравнений второй и высших степеней, они играют основную роль в алгебре и во многих разделах математического анализа. Дуальные же и двойные числа не имеют никакого отношения к теории квадратных уравнений с вещественными коэффициентами и вообще сравнительно мало связаны с алгеброй. Основные применения эти числа находят в геометрии (некоторые применения эти системы комплексных чисел находят также в теории чисел).
Основные применения двойных чисел относятся к неевклидовой геометрии Лобачевского и к некоторым другим геометриям, отличным от привычной геометрии Евклида (например, к так называемой псевдоевклидовой геометрии, играющей фундаментальную роль в физической теории относительности).
В нашей работе исследуются дуальные и двойные числа, а также применение этих чисел в геометрии Евклида и в геометрии Лобачевского.
Глава I. Определение дуальных и двойных чисел
1.1 Дуальные числа
Сложение, вычитание и умножение дуальных чисел определяется формулами:
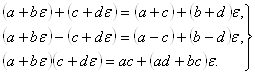 (1)
(1)
Последняя из этих формул показывает, что произведение дуального числа 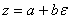 Вана другое число
Вана другое число 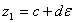 Вабудет вещественным лишь в том случае, когда
Вабудет вещественным лишь в том случае, когда 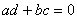 ; если
; если 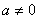 , то последнее равенство можно записать в виде
, то последнее равенство можно записать в виде 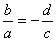 . Вещественным, в частности, является произведение чисел
. Вещественным, в частности, является произведение чисел 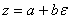 Ваи
Ваи 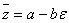 :
:
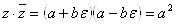 (2)
(2)
Число 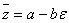 Ваназывают сопряжённым числу
Ваназывают сопряжённым числу 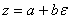 Ва(и обратно,
Ва(и обратно, 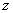 Васопряжено
Васопряжено 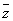 ); корень квадратный
); корень квадратный 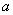 Ваиз произведения
Ваиз произведения 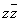 Ва(совпадающий с полусуммой
Ва(совпадающий с полусуммой 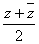 Васопряжённых чисел
Васопряжённых чисел 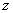 Ваи
Ваи 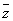 ) называют модулем дуального числа
) называют модулем дуального числа 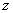 Ваи обозначают через
Ваи обозначают через 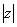 Ва(отметим, что модуль дуального числа может быть и отрицательным). Сумма
Ва(отметим, что модуль дуального числа может быть и отрицательным). Сумма 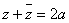 Вадвух сопряжённых чисел является вещественной; разность
Вадвух сопряжённых чисел является вещественной; разность 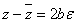 Ваявляется числом чисто мнимым (т.е. отличается от
Ваявляется числом чисто мнимым (т.е. отличается от 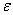 Валишь вещественным множителем). Заметим ещё, что, в полной аналогии с обыкновенными комплексными числами, дуальное число
Валишь вещественным множителем). Заметим ещё, что, в полной аналогии с обыкновенными комплексными числами, дуальное число 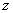 Ватогда и только тогда совпадает со своим сопряжённым
Ватогда и только тогда совпадает со своим сопряжённым 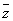 , когда оно является вещественным. Также и справедливые для комплексных чисел формулы (3)
, когда оно является вещественным. Также и справедливые для комплексных чисел формулы (3)
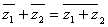 ,
, 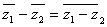 ,
, 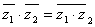 ,
, 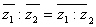 Ва(3)
Ва(3)
полностью остаются в силе для дуальных чисел.
Правило деления на дуальное число 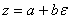 Вамы теперь можем записать так:
Вамы теперь можем записать так:
 . (4)
. (4)
Отсюда видно, что для возможности деления на дуальное число 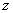 Ванеобходимо, чтобы модуль
Ванеобходимо, чтобы модуль 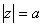 Ваэтого числа был отличен от нуля; при этом, в противоположность обыкновенным комплексным числам, дуальное число нулевого модуля само может быть отличным от нуля. В тех случаях, когда невозможность деления на числа нулевого модуля явится для нас затруднением, мы будем считать, что частные
Ваэтого числа был отличен от нуля; при этом, в противоположность обыкновенным комплексным числам, дуальное число нулевого модуля само может быть отличным от нуля. В тех случаях, когда невозможность деления на числа нулевого модуля явится для нас затруднением, мы будем считать, что частные 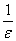 Ваи
Ваи 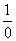 Ваявляются числами новой природы, которые условимся обозначать через
Ваявляются числами новой природы, которые условимся обозначать через 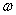 Ваи
Ваи 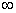 ; введём также в рассмотрение всевозможные числа вида
; введём также в рассмотрение всевозможные числа вида 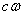 , где
, где 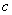
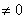 Вавещественно. Тогда любое дуальное число будет иметь обратное:
Вавещественно. Тогда любое дуальное число будет иметь обратное:
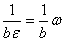 Вапри
Вапри 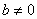 ;
; 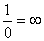 .
.
Правила действий над символом 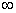 Ваопределяются следующими формулами:
Ваопределяются следующими формулами:
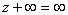 ,
, 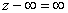 ,
, 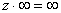 ,
, 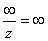 ,
, 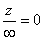 , (5)
, (5)
здесь 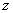 - произвольное число, причём в среднем равенстве
- произвольное число, причём в среднем равенстве 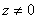 , а во втором и в двух последних
, а во втором и в двух последних 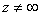 (
(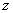 Вав этих формулах может быть и числом вида
Вав этих формулах может быть и числом вида 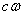 ); правила действий над числами
); правила действий над числами  Ваопределяются так:
Ваопределяются так:
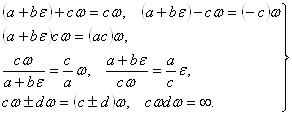 (6)
(6)
Положим ещё
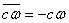 ,
, 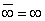 ; (6а)
; (6а)
тогда для расширенного (введением чисел 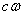 ,
, 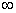 ) множества дуальных чисел сохраняет силу равенство
) множества дуальных чисел сохраняет силу равенство 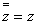 Ваи все правила (3).
Ваи все правила (3).
Число  Ванулевого модуля можно характеризовать тем, что существует отличное от нуля дуальное число
Ванулевого модуля можно характеризовать тем, что существует отличное от нуля дуальное число 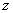 , равное
, равное 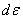 , произведение которого на число
, произведение которого на число  Варавняется нулю:
Варавняется нулю:
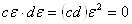 . (7)
. (7)
Поэтому эти числа называют делителями нуля.
Дуальные числа ненулевого модуля 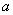 Ваможно также записать в форме, близкой к тригонометрической форме комплексного числа:
Ваможно также записать в форме, близкой к тригонометрической форме комплексного числа:
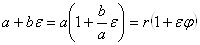 . (8)
. (8)
Здесь 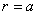 Ваесть модуль числа
Ваесть модуль числа 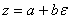 , а отношение
, а отношение 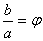 Ваназывается аргументом этого числа и обозначается через Argz(rможет быть произвольным вещественным числом, отличным от нуля;
Ваназывается аргументом этого числа и обозначается через Argz(rможет быть произвольным вещественным числом, отличным от нуля; 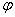 - произвольным вещественным числом). Очевидно, что вещественные числа
- произвольным вещественным числом). Очевидно, что вещественные числа 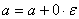 Вахарактеризуются равенством нулю их аргумента; сопряжённые дуальные числа
Вахарактеризуются равенством нулю их аргумента; сопряжённые дуальные числа 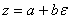 Ваи
Ваи 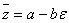 Ваимеют одинаковый модуль r и противоположные аргументы
Ваимеют одинаковый модуль r и противоположные аргументы 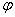 Ваи
Ваи 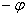 .
.
Форма (8) записи дуальных чисел очень удобна в тех случаях, когда эти числа приходится перемножать или делить. Действительно,
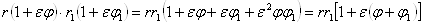 ; (9)
; (9)
следовательно, модуль произведения двух дуальных чисел равен произведению модулей сомножителей[1]
, а аргумент произведения - сумме аргументов. Отсюда вытекает, что модуль частного двух дуальных чисел равен частному модулей этих чисел, а аргумент частного тАУ разности соответствующих аргументов:
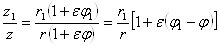 . (10)
. (10)
Наконец, из этих правил выводятся также и законы, позволяющие возвышать дуальное число в любую степень и извлекать из него корень:
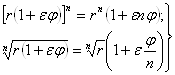 Ва(11)
Ва(11)
(из последней формулы вытекает, что корень нечётной степени из дуального числа при 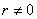 Ваопределяется однозначно; корень же чётной степени не существует, если r<0, и имеет два значения, еслиr>0[2]
Ваопределяется однозначно; корень же чётной степени не существует, если r<0, и имеет два значения, еслиr>0[2]
).
1.2 Двойные числа
В полной аналогии со всем изложенным выше назовём двойные числа 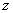 Ваи
Ваи 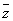 Васопряжёнными, если они имеют вид
Васопряжёнными, если они имеют вид
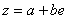 Ваи
Ваи 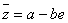 .
.
Сумма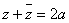 Ваи произведение
Ваи произведение 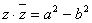 Васопряжённых двойных чисел вещественны; корень квадратный из числа
Васопряжённых двойных чисел вещественны; корень квадратный из числа 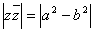 , знак которого совпадает со знаком большего по абсолютной величине из вещественных чисел a и , называется модулем числа
, знак которого совпадает со знаком большего по абсолютной величине из вещественных чисел a и , называется модулем числа 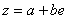 Ваи обозначается через
Ваи обозначается через 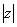 . Легко проверить, что для двойных чисел остаются в силе все формулы (3); кроме того, ясно, что равенство
. Легко проверить, что для двойных чисел остаются в силе все формулы (3); кроме того, ясно, что равенство 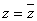 Вахарактеризует вещественные числа
Вахарактеризует вещественные числа 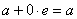 , а равенство
, а равенство 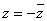 Ва- чисто мнимые числа
Ва- чисто мнимые числа 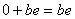 .
.
Сложение, вычитание, умножение и деление двойных чисел определяются формулами
 Ва(12)
Ва(12)
Отсюда следует, что и здесь деление на 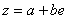 Вавозможно лишь в тех случаях, когда
Вавозможно лишь в тех случаях, когда 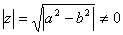 . Двойные числа
. Двойные числа 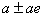 , модуль которых равен нулю, называются делителями нуля (заметим, что
, модуль которых равен нулю, называются делителями нуля (заметим, что 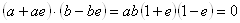 ). В некоторых случаях оказывается удобным считать частные
). В некоторых случаях оказывается удобным считать частные 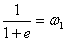 ,
, 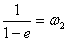 Ваи
Ваи 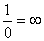 Вачислами новой природы; при этом оказывается необходимым ещё расширить понятие двойного числа, введя дополнительно произведения
Вачислами новой природы; при этом оказывается необходимым ещё расширить понятие двойного числа, введя дополнительно произведения 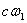 Ваи
Ваи 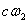 Вановых чисел
Вановых чисел 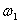 Ваи
Ваи 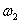 Вана всевозможные вещественные числа c и частные
Вана всевозможные вещественные числа c и частные 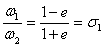 Ваи
Ваи 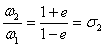 . Правила действия над символами
. Правила действия над символами 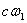 ,
, 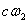 ,
, 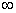 ,
, 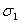 Ваи
Ваи 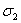 Ваопределяются формулами (5) и рядом соотношений, родственных (6), например:
Ваопределяются формулами (5) и рядом соотношений, родственных (6), например:
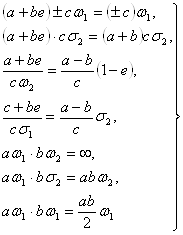 Ва(13)
Ва(13)
и т. д. Естественно также положить
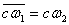 ,
, 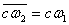 ,
, 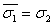 ,
, 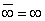 , (13а)
, (13а)
что обеспечит выполнение для расширенного указанным образом множества двойных чисел равенства 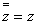 Ваи всех соотношений (3).
Ваи всех соотношений (3).
Двойные числа ненулевого модуля можно также записать в форме, аналогичной форме (8) записи дуальных чисел. Пусть 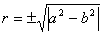 Ва- модуль
Ва- модуль 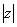 Вадвойного числа; далее
Вадвойного числа; далее
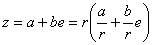 .
.
Из определения модуля следует, что 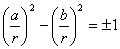 Ваи что большая (по абсолютной величине) из дробей
Ваи что большая (по абсолютной величине) из дробей 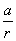 Ваи
Ваи 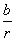 Ваположительна. Отсюда вытекает, что
Ваположительна. Отсюда вытекает, что
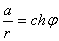 ,
, 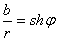 Ваили
Ваили 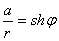 ,
, 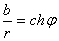 , (14)
, (14)
где 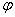 Ваесть некоторое число (определённое формулами (14)), а
Ваесть некоторое число (определённое формулами (14)), а 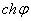 Ваи
Ваи 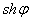 ВатАУ гиперболический косинус и гиперболический синус аргумента
ВатАУ гиперболический косинус и гиперболический синус аргумента 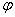 .
.
Таким образом, имеем
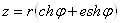 Ваили
Ваили 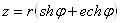 . (15)
. (15)
величина 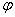 Ваназывается аргументом двойного числа z и обозначается через Argz[3]
Ваназывается аргументом двойного числа z и обозначается через Argz[3]
.
Форма (15) записи двойных чисел очень удобна в тех случаях, когда приходится перемножать два или несколько двойных чисел. Действительно, из формул сложения гиперболических функций следует, что
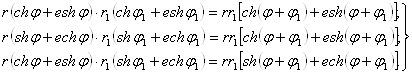 Ва(16)
Ва(16)
Таким образом, модуль произведения двух двойных чисел равен произведению модулей сомножителей, а аргумент произведения тАУ сумме аргументов; при этом произведение имеет первую или вторую из форм (15) в зависимости от того, имеют ли сомножители одну и ту же или разные формы. Из формул (16) сразу вытекают правила деления двойных чисел:
 ;
;
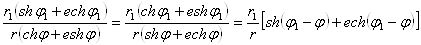 . (17)
. (17)
Из формул (16) получаются также правила, позволяющие возводить двойное число в любую целую положительную степень и извлекать из него корень степени :
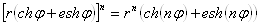 ,
,
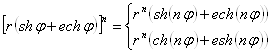
при
нечётном,
при чётном;
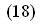
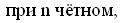
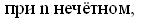

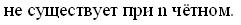
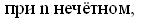
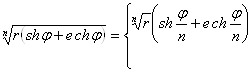
Глава II.
2.1 Дуальные числа как ориентированные прямые плоскости.
Две ориентированные прямые будем называть параллельными лишь в том случае, если они параллельны в обычном смысле и направления этих прямых совпадают (рис. 1, а); параллельные прямые противоположных направлений будем называть противопараллельными (рис. 1, б).

аВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа б
Рис. 1
Под расстоянием от прямой a до не пересекающей её прямой будем понимать ориентированное расстояние {a,} от a до , т.е. ориентированное расстояние от произвольной точки прямой a до прямой ; очевидно, что {a,}=-{,a}, если aи параллельны, и {a,}={,a}, если a и противопараллельны.
Полярные координаты точек плоскости определяются заданием некоторой точки O (полюса системы координат) и проходящей через O ориентированной прямойo (полярной оси); координатами точки M служат расстояние r=OM этой точки от полюса и угол 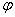 ={o,m}, образованный с oориентированной прямой m, соединяющей OиM. Аналогично этому можно определить полярные координаты ориентированных прямых плоскости, для задания которых надо также указать некоторую ориентированную прямую o (полярную ось) и лежащую на o точку O (полюс); координатами прямой l служат угол
={o,m}, образованный с oориентированной прямой m, соединяющей OиM. Аналогично этому можно определить полярные координаты ориентированных прямых плоскости, для задания которых надо также указать некоторую ориентированную прямую o (полярную ось) и лежащую на o точку O (полюс); координатами прямой l служат угол 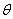 ={o,l}, образованный l с полярной осью o, и ориентированное расстояние ={O,L} от O до точки L пересечения lи o (рис. 2,а). Очевидно, что координата ориентированной прямой lможет иметь любое значение, заключённое между
={o,l}, образованный l с полярной осью o, и ориентированное расстояние ={O,L} от O до точки L пересечения lи o (рис. 2,а). Очевидно, что координата ориентированной прямой lможет иметь любое значение, заключённое между 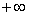 Ваи
Ваи 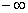 ; координата
; координата 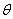 ВатАУ любое значение, заключённое между 0 и 2
ВатАУ любое значение, заключённое между 0 и 2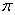 . Естественно считать, что
. Естественно считать, что 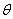 =0 для прямых, параллельных полярной оси o, и
=0 для прямых, параллельных полярной оси o, и 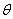 =
=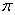 Вадля прямых, противопараллельных o; если прямая не пересекает оси o, то координаты она не имеет (можно считать, что в этом случае
Вадля прямых, противопараллельных o; если прямая не пересекает оси o, то координаты она не имеет (можно считать, что в этом случае 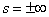 ).
).
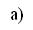
Условимся сопоставлять ориентированной прямой l с полярными координатами 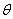 Ваи дуальное число
Ваи дуальное число
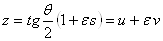 ,
, 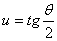 ,
, 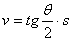 Ва(19)
Ва(19)
(рис. 2). При этом параллельным o прямым, для которых 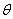 =0, естественно относить числа нулевого модуля, т.е. делители нуля
=0, естественно относить числа нулевого модуля, т.е. делители нуля 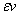 . Чтобы установить точное соответствие между параллельными o прямыми и делителями нуля, заметим, что расстояние d={O,l} не параллельной o прямой l от полюса O равно
. Чтобы установить точное соответствие между параллельными o прямыми и делителями нуля, заметим, что расстояние d={O,l} не параллельной o прямой l от полюса O равно
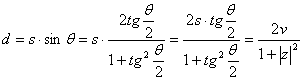 Ва(20)
Ва(20)
(рис. 2, а). Чтобы формула (20) сохранила силу и для параллельной o прямой m, отстоящей от o на расстоянии {o,m}=d, то этой прямой нужно сопоставить число
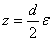 Ва(т.е.
Ва(т.е.  , где u=0 и
, где u=0 и 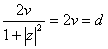 ).
).
Двум пересекающим o прямым lи l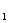 , отличающимся только направлением и, следовательно, имеющим полярные координаты (
, отличающимся только направлением и, следовательно, имеющим полярные координаты (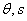 ) и (
) и (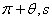 ), отвечают дуальные числа
), отвечают дуальные числа
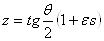
и
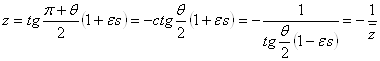 .
.
Считая, что это соотношение сохраняет силу и для прямых, не пересекающих o, условимся относить противопараллельной o прямой m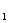 , отстоящей от o на расстоянии {o,m
, отстоящей от o на расстоянии {o,m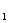 }=d
}=d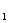 , число
, число
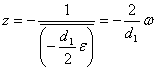
(заметим, что если расстояние {o,m} от o до параллельной o прямой m, совпадающей по положению на плоскости с прямой m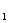 , равно d, то d=-d
, равно d, то d=-d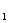 ). Прямой o
). Прямой o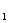 , отличающейся только направлением от полярной оси o (противооси), мы сопоставим число
, отличающейся только направлением от полярной оси o (противооси), мы сопоставим число 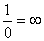 .
.
Тем самым мы устанавливаем полное соответствие между ориентированными прямыми плоскости и дуальными числами, включая сюда также и числа вида w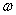 , где w
, где w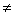 0 вещественно, и число
0 вещественно, и число 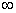 .
.
Очевидно, что вещественным числам 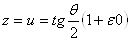 Ваотвечают проходящие через полюс O прямые; числам модуля 1 тАУ перпендикулярные o прямые; чисто мнимым числам v
Ваотвечают проходящие через полюс O прямые; числам модуля 1 тАУ перпендикулярные o прямые; чисто мнимым числам v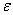 Ва(числам нулевого модуля) и числам бесконечного модуля w
Ва(числам нулевого модуля) и числам бесконечного модуля w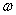 Ваотвечают параллельные и противопараллельные оси o прямые. Сопряжённым числам
Ваотвечают параллельные и противопараллельные оси o прямые. Сопряжённым числам 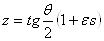 Ваи
Ваи 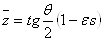 Ваотвечают прямые симметричные относительно полюса O; противоположным числам
Ваотвечают прямые симметричные относительно полюса O; противоположным числам 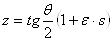 Ваи
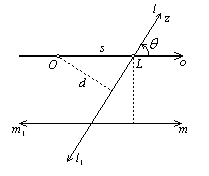
Ваи 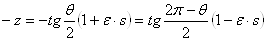 ВатАУ прямые, симметричные относительно полярной оси o (т.е. прямые, пересекающие o в одной и той же точке L и образующие сo равные углы
ВатАУ прямые, симметричные относительно полярной оси o (т.е. прямые, пересекающие o в одной и той же точке L и образующие сo равные углы 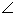 {o,z}=
{o,z}=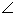 {-z,o}; см. рис. 2, б); числам z и
{-z,o}; см. рис. 2, б); числам z и 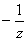 Ваотвечают прямые, отличающиеся только направлением. Таким образом, равенства
Ваотвечают прямые, отличающиеся только направлением. Таким образом, равенства
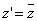 Ва(а),
Ва(а), 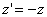 Ва(б),
Ва(б), 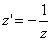 (в)Ва (21)
(в)Ва (21)
можно понимать как записи определённых преобразований в множестве ориентированных прямых плоскости: симметрии относительно точки O, симметрии относительно прямой o и переориентации (изменения направления всех прямых плоскости на противоположное).
Выясним теперь, как записываются с помощью дуальных чисел произвольные движения (к числу которых отнесём и переориентацию, также не меняющую расстояний между точками плоскости).
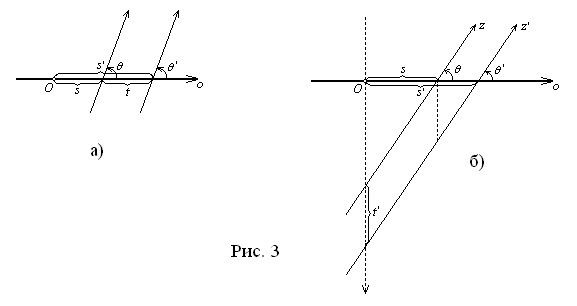
Параллельный перенос вдоль o на расстояние t переводит прямую, которой отвечает дуальное число
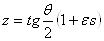 ,
,
в прямую, которой отвечает число
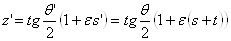
(рис. 3, а). Отсюда вытекает, что этот параллельный переносВа можно записать так:
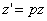 , где
, где 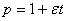 ,
,  Ва(22)
Ва(22)
(т.к. 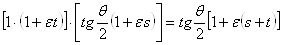 ).
).
Параллельный перенос на расстояние t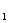 Вав направлении, перпендикулярном o, переводит прямую
Вав направлении, перпендикулярном o, переводит прямую
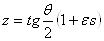
в прямую
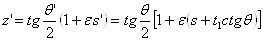
(рис. 3, б). Но
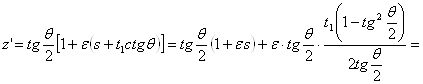
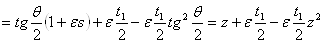 .
.
Последнюю формулу можно записать в более изящном виде. Заметим, что
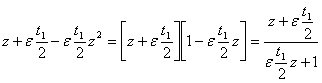 ;
;
таким образом, рассматриваемый параллельный перенос записывается формулой
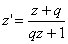 , где
, где 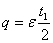 ,
, 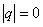 . (22, а)
. (22, а)
Отсюда вытекает, что произвольный параллельный перенос, т.е. перенос на расстояние t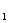 Вав направлении o и на расстояние t
Вав направлении o и на расстояние t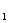 Вав направлении l
Вав направлении l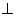 o, записывается формулой
o, записывается формулой
 ,
, 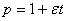 ,
, 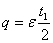 ,
,
или, если ввести обозначение 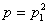 Ва(т.е.
Ва(т.е. 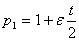 ) и воспользоваться тем, что
) и воспользоваться тем, что 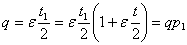 ,
, 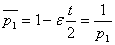 ,
, 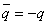 , формулой
, формулой
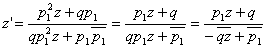 , (23)
, (23)
где 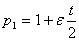 ,
, 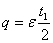 ,
, 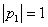 ,
, 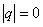 .
.
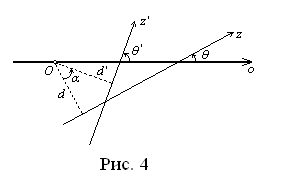
Перейдём теперь к вращениям плоскости. Очевидно, что поворот вокруг O на угол 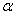 Вапереводит прямую
Вапереводит прямую 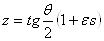 Вав прямую
Вав прямую 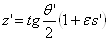 , где
, где 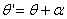 Ва(рис. 4). Таким образом,
Ва(рис. 4). Таким образом,
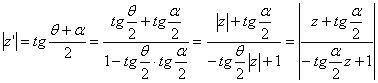 Ва(24)
Ва(24)
(здесь используется то, что если z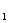 иz
иz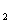 тАУ дуальные числа, то
тАУ дуальные числа, то 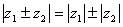 ,
, 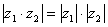 Ваи
Ваи 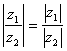 ). Далее, если dиd′тАУ расстояния прямых zиz′ отполюса , то
). Далее, если dиd′тАУ расстояния прямых zиz′ отполюса , то
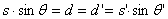
поэтому
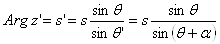 .
.
С другой стороны, поскольку 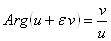 , то
, то
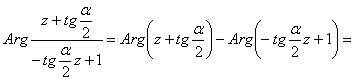
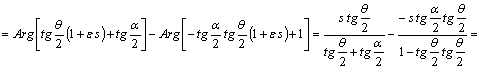
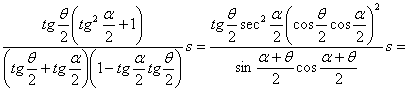
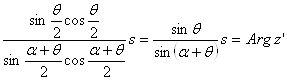 .Ва (24а)
.Ва (24а)
Из (24) и (24а) следует, что наше вращение записывается формулой
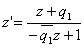 , (25)
, (25)
где 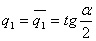 ,
, 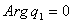 .
.
Наконец, самое общее движение представляет собой поворот (25) вокруг O на некоторый угол 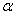 , причём это вращение может сопровождаться ещё параллельным переносом (33):
, причём это вращение может сопровождаться ещё параллельным переносом (33):
 .
.
В другом виде это преобразование можно записать так:
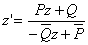 , (26а)
, (26а)
где 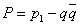 ,
, 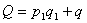 .
.
Возможно, также, что исходное движение представляет собой симметрию (21б) относительно прямой o, сопровождаемую преобразованием (36а) (вращением вокруг O и параллельным переносом):
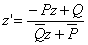 . (26б)
. (26б)
Наконец, движение может представлять собой переориентацию (21в), сопровождаемую одним из преобразований (36а) или (36б):
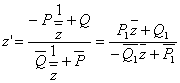 , (26в)
, (26в)
где 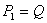 ,
, 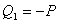 , или
, или
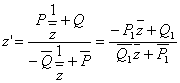 , (26г)
, (26г)
где 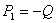 ,
, 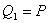 .
.
Очевидно, что ориентированный угол 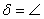 {
{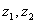 } между прямыми
} между прямыми 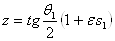 Ваи
Ваи 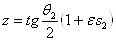 Варавен
Варавен 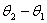 Ва(рис. 5, а)
Ва(рис. 5, а)
Это можно записать так:
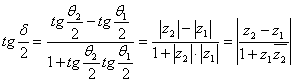 .
.
Полученный результат можно также представить в следующей симметричной форме:
 . (27)
. (27)
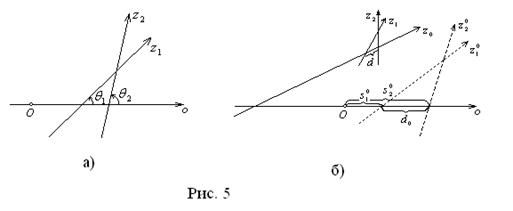
Найдём теперь ориентированное расстояние d={[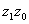 ],[
],[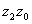 ]} между точками [
]} между точками [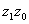 ] и [
] и [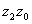 ] пересечения определённой прямой
] пересечения определённой прямой 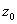 Вас двумя другими прямыми
Вас двумя другими прямыми 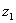 Ваи
Ваи 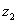 Ва(рис. 5, б). Очевидно, что расстояние d
Ва(рис. 5, б). Очевидно, что расстояние d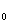 между точками пересечения прямой o с прямыми
между точками пересечения прямой o с прямыми 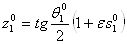 Ваи
Ваи 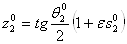 Варавно
Варавно
 .
.
Пример движения, переводящего данную прямую 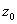 Вав прямую o, даётся формулой
Вав прямую o, даётся формулой
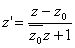 ;
;
это движение переводит прямые 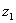 Ваи
Ваи 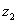 Вав прямые
Вав прямые 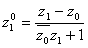 Ваи
Ваи 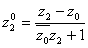 . Отсюда получаем
. Отсюда получаем
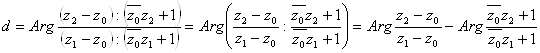 .(28)
.(28)
Условием того, что прямые 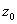 ,
, 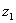 Ваи
Ваи 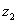 Вапересекаются в одной точке, является равенство нулю расстояния между точками пересечения
Вапересекаются в одной точке, является равенство нулю расстояния между точками пересечения 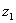 Ваи
Ваи 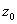 Вас
Вас 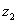 , т.е., в силу формулы (28), вещественность отношения
, т.е., в силу формулы (28), вещественность отношения 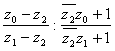 .
.
Это условие можно переписать ещё так:
 . (29)
. (29)
Следовательно, тАЬуравнение точкитАЭ, т.е. условие, которому удовлетворяют прямые 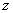 , проходящие через одну точку [
, проходящие через одну точку [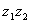 ], имеет вид
], имеет вид
 ,
,
или
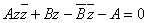 , AтАУ чисто мнимое (30)
, AтАУ чисто мнимое (30)
(здесь 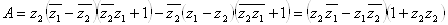 ,Ва
,Ва  ).
).
Найдём теперь условие того, что четыре ориентированные точки 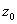 ,
, 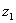 ,
, 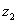 Ваи
Ваи 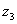 Вапринадлежат одной ориентированной окружности. При этом под ориентированной окружностью мы здесь понимаем совокупность всех ориентированных прямых l, ориентированное расстояние {O,l} которых от данной точки O (центра окружности) имеет фиксированное значение r. Число r называется радиусом окружности; таким образом, радиус ориентированной окружности может быть как положительным, так и отрицательным. Из определения ориентированного расстояния {O,l} от точки O до прямой l следует, что радиус ориентированной окружности будет положительным, если направление обхода противоположно направлению вращения часовой стрелки, и отрицательным в противном случае.
Вапринадлежат одной ориентированной окружности. При этом под ориентированной окружностью мы здесь понимаем совокупность всех ориентированных прямых l, ориентированное расстояние {O,l} которых от данной точки O (центра окружности) имеет фиксированное значение r. Число r называется радиусом окружности; таким образом, радиус ориентированной окружности может быть как положительным, так и отрицательным. Из определения ориентированного расстояния {O,l} от точки O до прямой l следует, что радиус ориентированной окружности будет положительным, если направление обхода противоположно направлению вращения часовой стрелки, и отрицательным в противном случае.
Можно показать, что четыре ориентированные прямые 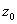 ,
, 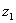 ,
, 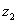 Ваи
Ваи 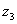 Вав том и только в том случае принадлежат одной ориентированной окружности или проходят через одну точку, если
Вав том и только в том случае принадлежат одной ориентированной окружности или проходят через одну точку, если
{[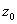
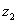 ],[
],[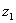
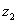 ]}
]}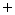 {[
{[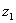
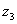 ],[
],[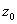
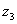 ]}={[
]}={[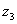
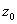 ],[
],[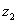
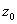 ]}
]}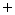 {[
{[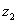
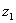 ],[
],[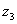
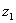 ]}. (31)
]}. (31)
Чтобы убедиться в этом, рассмотрим рис. 33, на котором изображены четыре ориентированные касательные 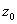 ,
, 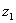 ,
, 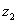 Ваи
Ваи 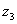 Ваориентированной окружности S, касающиеся S соответственно в точках M,N,PиQ; точки [
Ваориентированной окружности S, касающиеся S соответственно в точках M,N,PиQ; точки [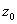
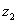 ], [
], [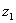
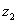 ], [
], [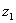
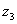 ] и [
] и [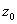
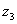 ] обозначены через A, B, CиD. При этом, очевидно, имеем
] обозначены через A, B, CиD. При этом, очевидно, имеем
{A,B}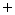 {C,D}={A,P}
{C,D}={A,P}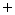 {P,B}
{P,B}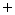 {C,Q}
{C,Q}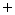 {Q,D}
{Q,D}
иВаВаВаВаВаВа
{D,A}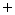 {B,C}={D,M}
{B,C}={D,M}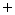 {M,A}
{M,A}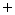 {B,N}
{B,N}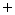 {N,C}
{N,C}
В силу известного свойства касательных к окружности
{A,P}={M,A}, {P,B}={B,N}, {C,Q}={N,C}, {Q,D}={D,M},
значит, во всех случаях выполняется условие (31)
{A,B}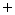 {C,D}={D,A}
{C,D}={D,A}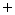 {B,C}.
{B,C}.
Нетрудно убедиться и в том, что если равенство (31) имеет место, то четыре прямые 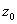 ,
, 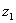 ,
, 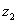 Ваи
Ваи 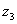 Вапринадлежат одной ориентированной окружности или проходят через одну точку.
Вапринадлежат одной ориентированной окружности или проходят через одну точку.
Воспользовавшись теперь формулой (28), мы можем переписать условие (31) следующим образом:
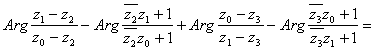
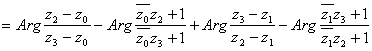 ,
,
или, несколько упростив левую часть последнего равенства и преобразовав правую,

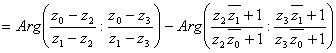 .
.
Но
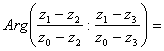
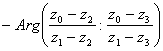
и
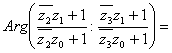
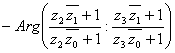
(т.к. 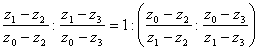 Ваи
Ваи 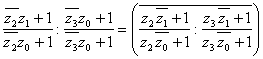 )
)
Таким образом, равенство (31) можно переписать в следующей простой форме:
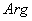
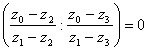 . (32)
. (32)
Дуальное число 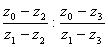 Ваестественно называть двойным отношением четырёх прямых
Ваестественно называть двойным отношением четырёх прямых 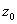 ,
, 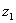 ,
, 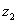 Ваи
Ваи 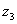 ; обозначать его будем символом W(
; обозначать его будем символом W(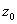 ,
,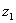 ,
,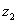 ,
,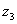 ). Таким образом, условием того, что четыре прямые
). Таким образом, условием того, что четыре прямые 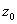 ,
, 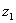 ,
, 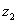 Ваи
Ваи 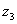 Вапринадлежат одной ориентированной окружности (ненулевого радиуса или окружности радиуса нуль тАУ точке), является вещественность двойного отношения W(
Вапринадлежат одной ориентированной окружности (ненулевого радиуса или окружности радиуса нуль тАУ точке), является вещественность двойного отношения W(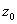 ,
,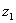 ,
,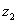 ,
,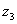 )=
)=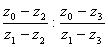 Ваэтих четырёх прямых.
Ваэтих четырёх прямых.
Последнему условию можно придать вид:
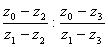 =
=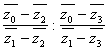 , (33)
, (33)
откуда вытекает, что уравнение ориентированной окружности (которая в частном случае может оказаться и точкой), определяемой тремя данными прямыми 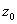 ,
, 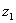 ,
, 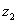 Ваи
Ваи 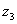 , имеет вид
, имеет вид
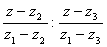 =
=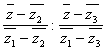 . (34)
. (34)
Таким образом, уравнение каждой ориентированной окружности (или точки) можно записать в форме (35):
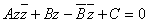 , A иC тАУ чисто мнимые. (35)
, A иC тАУ чисто мнимые. (35)
Нетрудно проверить, что и, обратно, уравнение (35) всегда выражает окружность (или точку).
Прямую уравнение (35) выражает при
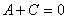 . (36)
. (36)
2.2 Двойные числа как ориентированные прямые плоскости Лобачевского
В полной аналогии с пунктом 2.1 ориентированным прямым плоскости Лобачевского можно сопоставить двойные числа. А именно, введём, как в пункте 2.1, полярную систему координат для прямых и отнесём каждой пересекающей полярную ось o ориентированной прямой l, имеющей полярные координаты 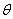 , , двойное число
, , двойное число
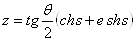 , (37)
, (37)
а расходящейся с oпрямой m, направленной в ту же сторону, что и o от их общего перпендикуляра PQ, тАУ число
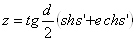 , (37а)
, (37а)
где d={m,o}={P,Q} тАУ кратчайшее ориентированное расстояние между прямыми mи o, т.е. ориентированное расстояние от o проекции P на прямую m общего перпендикуляра прямых mи o, тАЩ={O,Q} тАУ ориентированное расстояние от полюса O системы координат до проекции Q общего перпендикуляра на o (рис. 6).
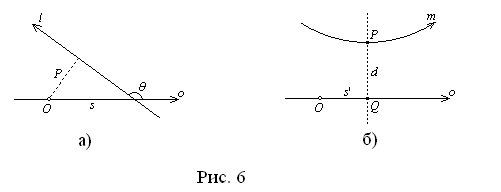
Далее, так как из формулы (37) вытекает, что двум пересекающим o прямым lи l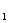 , отличающимся только направлением, соответствуют двойные числа
, отличающимся только направлением, соответствуют двойные числа
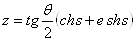
и
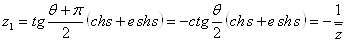 ,
,
то прямой m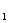 , отличающейся только направлением ототвечающей числу (37а) расходящейся с o прямой m, сопоставим число
, отличающейся только направлением ототвечающей числу (37а) расходящейся с o прямой m, сопоставим число
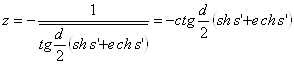 . (37б)
. (37б)
Прямые, параллельные оси o, можно рассматривать как предельный случай пересекающих o прямых, отвечающий равенству нулю угла 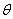 , или как предельный случай расходящихся с o прямых, отвечающий равенству нулю расстояний d. Так как из формул (37) и (37а) следует, что
, или как предельный случай расходящихся с o прямых, отвечающий равенству нулю расстояний d. Так как из формул (37) и (37а) следует, что 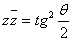 , соответственно
, соответственно 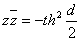 , то естественно отнести параллельным o прямым, направленным в ту же сторону, что и o, делители нуля, т.е. числа вида
, то естественно отнести параллельным o прямым, направленным в ту же сторону, что и o, делители нуля, т.е. числа вида 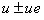 . При этом прямым, параллельным o в положительном или отрицательном направлении, отвечают числа
. При этом прямым, параллельным o в положительном или отрицательном направлении, отвечают числа 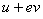 , для которых
, для которых 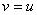 Ваили
Ваили 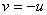 , т.к. из (37) и (37а) вытекает, что соотношение
, т.к. из (37) и (37а) вытекает, что соотношение 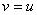 Варавносильно равенству
Варавносильно равенству 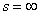 Ваили
Ваили 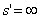 , а соотношение
, а соотношение 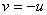 ВатАУ равенству
ВатАУ равенству 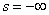 Ваили
Ваили 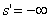 . Из формул неевклидовой тригонометрии следует, что ориентированное расстояние ={O,l} от полюса O до пересекающей o прямой l (рис. 6), отвечающей двойному числу
. Из формул неевклидовой тригонометрии следует, что ориентированное расстояние ={O,l} от полюса O до пересекающей o прямой l (рис. 6), отвечающей двойному числу 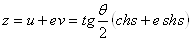 , находится из соотношения
, находится из соотношения
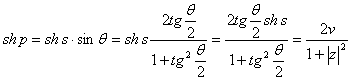 . (38)
. (38)
Поэтому двум параллельным o прямым и', удалённым от O на расстояние {O, }={O, '}=, надо отнестиВа числа 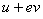 Ва(где
Ва(где 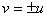 ), для которых
), для которых 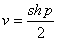 , т.е. числа
, т.е. числа
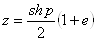 Ваи
Ваи 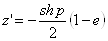 .
.
Наконец, исходя из соотношения 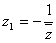 , связывающего двойные числа zи z
, связывающего двойные числа zи z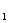 , отвечающие пересекающим ось o или расходящимся с o прямым, отличающимся одна от другой лишь направлением, сопоставим противопараллельным o прямым n
, отвечающие пересекающим ось o или расходящимся с o прямым, отличающимся одна от другой лишь направлением, сопоставим противопараллельным o прямым n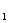 Ваи n
Ваи n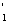 (т.е. прямым, параллельным o и противоположно направленным), удалённым от O на расстояние {O, n
(т.е. прямым, параллельным o и противоположно направленным), удалённым от O на расстояние {O, n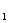 }={O,n
}={O,n }=p
}=p , числа
, числа
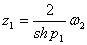 Ваи
Ваи 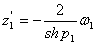 ,
,
где 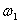 Ваи
Ваи 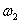 ВатАУ числа, обратные делителям нуля:
ВатАУ числа, обратные делителям нуля: 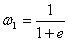 ,
, 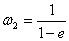 Ва(если и n
Ва(если и n тАУ две прямые, отличающиеся только направлением, то ={O, }=тАУ{O, Вместе с этим смотрят:
тАУ две прямые, отличающиеся только направлением, то ={O, }=тАУ{O, Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы