Рiзницевий метод розв'язання крайових задач для звичайних диференцiальних рiвнянь

Мiнiстерство освiти i науки Украiни

Днiпропетровський нацiональний унiверситет iм. Олеся Гончара

Механiко-математичний факультет

Кафедра прикладноi газовоi динамiки i тепломасообмiну

Рiзницевий метод розв'язання крайових задач для

звичайних диференцiальних рiвнянь

Виконав: студент групи МТ-07-1

Коваленко О.А.

Керiвник практики: асистент

Губiн О.РЖ.

Днiпропетровськ

2010

Змiст

I. Теоретична частина

I.1. Рiзницевий метод розв'язання крайових задач для

звичайних диференцiальних рiвнянь

I.2. Метод прогонки

II. Практична частина

II.1. Формулювання завдання

II.2. Лiстинг програми на алгоритмiчнiй мовi Turbo Pascal

II.3. Результати обчислень

Висновки

Список використаноi лiтератури

I. Теоретична частина

I.1 Рiзницевий метод розв'язання крайових задач для звичайних диференцiальних рiвнянь

Крайова задача тАУ це задача вiдшукання часткового розв'язку рiвняння

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(1)

на вiдрiзку 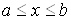, у якiй додатковi умови накладаються на значення функцii U(x) i ii похiдних бiльш нiж в однiй точцi цього вiдрiзка. Очевидно, що крайовi задачi можливi для рiвнянь порядку не нижче другого.

Розглянемо крайову задачу для нелiнiйного рiвняння другого порядку:

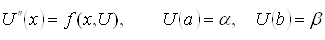ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(2)

з крайовими умовами першого роду.

Уведемо на [a; b] сiтку , яку для спрощення будемо вважати рiвномiрною. Наближено виразимо другу похiдну вiд розв'язку через значення розв'язку у вузлах сiтки 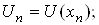Ванаприклад, скористаiмося найпростiшою апроксимацiiю:

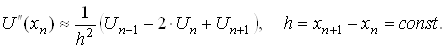ВаВаВаВа Ва(3)

Таку апроксимацiю можна записати в кожному внутрiшньому вузлi сiтки xn, 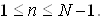ВаЯкщо пiдставити ii в рiвняння (2), то рiвняння стане наближеним; точно задовольняти цьому рiвнянню буде вже не шуканий розв'язок U(x), а деякий наближений розв'язок 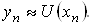ВаВиконуючи цю пiдстановку, отримаiмо систему нелiнiйних алгебраiчних рiвнянь

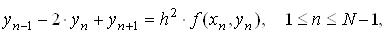ВаВаВаВаВаВаВаВаВа Ва(4)

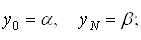
останнi два рiвняння апроксимують крайовi умови.

Якщо 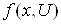Ваобмежена й неперервна разом зi своiми другими похiдними, так, що iснуi обмежена й неперервна 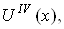а також 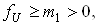Вато при Варiзницевий розв'язок рiвномiрно збiгаiться до точного iз другим порядком точностi.

Розв'язок системи (4) можна отримати методом послiдовних наближень у наступнiй формi:

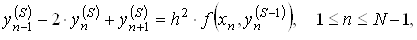ВаВаВаВаВаВаВа Ва(5)

Тодi для визначення 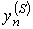Вана кожнiй iтерацii виходить лiнiйна система, розв'язувана алгебраiчною прогонкою. РЖтерацii (5) збiгаються при виконаннi умови:

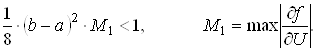ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(6)

Умова (6) i достатньою, але вона близька до необхiдноi: бiльш складнi оцiнки показують, що якщо Вато iтерацii (5) можуть розбiгатися.

Рiзницевий метод маi своi труднощi, пов'язанi в основному з розв'язанням алгебраiчноi системи рiвнянь. Однак цi труднощi успiшно долаються. Метод природно переноситься на рiвняння високого порядку, причому трудомiсткiсть обчислень майже не зростаi. Його чисельна стiйкiсть звичайно хороша.

I.2Метод прогонки

Найбiльш важливим окремим випадком методу Гауса i метод прогонки, застосовуваний до систем лiнiйних алгебраiчних рiвнянь iз тридiагональною матрицею. Такi системи звичайно записують у канонiчному виглядi:

ВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(7)

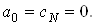
Метод прогонки зводиться до вiдшукання невiдомих Ваз наступних рекурентних спiввiдношень:

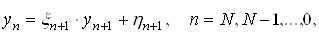ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(8)

ВаВаВаВаВа Ва(9)

Формули (8) i формулами зворотного ходу, а (9) тАУ формулами прямого ходу.

Для початку розрахунку потрiбно задати величини Ваi 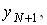Ваякi невiдомi. Однак перед цими величинами у формулах стоять множники, рiвнi нулю. Це дозволяi почати обчислення, поклавши, наприклад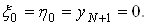

Якщо виконано умову переваги дiагональних елементiв

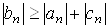ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(10)

(причому хоча б для одного n маi мiсце нерiвнiсть), то у формулах прямого ходу (9) не виникаi дiлення на нуль, i тим самим вихiдна система (7) маi iдиний розв'язок. При виконаннi умови (10) формули прогонки стiйкi щодо похибок округлення й дозволяють успiшно розв'язувати системи рiвнянь iз кiлькома сотнями невiдомих. У практичних розрахунках для добре обумовлених систем типу (7) прогонка часто виявляiться досить стiйкою навiть при порушеннi умови переваги дiагональних елементiв.

крайова задача рiзницевий метод

II.Практична частина

II.1 Формулювання завдання

Дано крайову задачу:

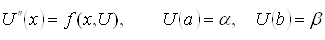
де 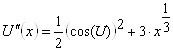Вата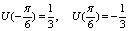

Для цiii задачi необхiдно:

1) застосовуючи рiзницевий метод одержати наближений розвтАЩязок у вузлах сiтки на заданому вiдрiзку;

2) визначити вузловi значення наближеного розвтАЩязку системи алгебраiчних рiвнянь за допомогою метода послiдовних наближень у сполученнi з методом прогонки

3) здiйснення розрахункiв на ЕОМ провести за допомогою програми на алгоритмiчнiй мовi Turbo Pascal

4) представити результати у в табличнiй i графiчнiй формi;

Вимоги до програмування

1. Алгоритм розвтАЩязання нелiнiйноi крайовоi задачi на основi рiзницевого методу необхiдно реалiзувати у виглядi програми на мовi Turbo Pascal.

2. Метод прогонки представити в програмах у виглядi окремоi процедури.

3. Для обчислення значень заданих функцiй створити окремi пiдпрограми.

4. Текст програми не повинен мати числових констант. Рекомендуiться використовувати тiльки змiннi.

5. Для iтерацiйного циклу при обчисленнi наближеного розвтАЩязку нелiнiйноi задачi передбачити ресурс iтерацii, при вичерпуваннi якого програма повинна повiдомляти про розбiжностi процесу.

II.2.Лiстинг програми на алгоритмiчнiй мовi Turbo Pascal

Program LP;

uses crt;

const n=40;

Ваag=-pi/6;

Ваbg=pi/6;

Ваalfa=1/3;

Ваbeta=-1/3;

Ваe=1e-5;

Ваs=4;

var i,k:integer;

Ваh,xi,max:real;

Ваy,y0:array[0.n+1] of real;

Ваa,b,c,d:array[0.n] of real;

Ваff:text;

function f(u,v:real):real;

var st:real;

begin

Ваif u>0 then st:=exp(ln(u)/3)

Ваelse if u<0 then st:=-exp(ln(-u)/3)

Ваelse st:=0;

Ваf:=sqr(cos(v))/2+3*st;

end;

procedure Progonka(np:integer; var ap,bp,cp,dp,yp:array of real);

var ip:integer;

Ваksi,eta:array[0.n+1] of real;

begin

Ваksi[0]:=0; eta[0]:=0;

Ваfor ip:=0 to np do

Ваbegin

Ваksi[ip+1]:=cp[ip]/(bp[ip]-ap[ip]*ksi[ip]);

Ваeta[ip+1]:=(ap[ip]*eta[ip]-dp[ip])/(bp[ip]-ap[ip]*ksi[ip]);

Ваend;

Ваfor ip:=np downto 0 do yp[ip]:=ksi[ip+1]*yp[ip+1]+eta[ip+1];

end;

begin

Ваclrscr;

Ваh:=(bg-ag)/n;

Ваa[0]:=0; b[0]:=-1; c[0]:=0; d[0]:=alfa;

Ваa[n]:=0; b[n]:=-1; c[n]:=0; d[n]:=beta;

Ваfor i:=1 to n-1 do

Ваbegin

Ваa[i]:=1; b[i]:=2; c[i]:=1;

Ваend;

Ваy[n+1]:=0;

Ваfor i:=0 to n do

Ваbegin

Ваxi:=ag+i*h;

Ваy[i]:=(beta*(xi-ag)+alfa*(bg-xi))/(bg-ag);

Ваend;

Ваk:=0;

Ваrepeat

Ваk:=k+1;

Ваy0:=y;

Ваfor i:=1 to n-1 do

Ваbegin

Ваxi:=ag+i*h;

Ваd[i]:=h*h*f(xi,y0[i]);

Ваend;

ВаProgonka(n,a,b,c,d,y);

Ваmax:=0;

Ваfor i:=0 to n do if max

Ваif k=100 then break;

Ваuntil max

Ваassign(ff,'f:\praktika.xls');

Ваrewrite(ff);

Ваwriteln(ff,'xi':6,#9,'yi':8);

Ваi:=0;

Ваwhile i

Ваbegin

Ваwriteln(ff,(ag+i*h):8:4,#9,y[i]:8:4);

Ваi:=i+s;

Ваend;

Ваwriteln(ff,bg:8:4,#9,y[n]:8:4);

Ваwriteln(ff);

Ваwriteln; writeln(ff,'k=',k);

Ваclose(ff);

Ваwriteln('rezultati raschetov vivedeni v fail praktika.xls');

Ваreadkey;

end.

II.3.Результати обчислень

Таблиця(наближений розвтАЩязок крайовоi задачi для рiзноi кiлькостi вузлiв та iтерацiй)

x_i	Ваk=4							k=1
	n=10		n=20		n=30		n=40
	y_i		y_i		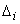y_i		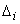y_i	y_i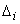
-0,5236	0,3333	0,0000	0,3333	0,0000	0,3333	0,0000	0,3333	0,3333	0,0000
-0,4189	0,2870	0,0349	0,2869	0,0000	0,2869	0,0000	0,2869	0,2866	0,1046
-0,3142	0,2212	0,1358	0,2210	0,0453	0,2209	0,0000	0,2209	0,2204	0,2263
-0,2094	0,1382	0,2903	0,1379	0,0726	0,1379	0,0726	0,1378	0,1371	0,5080
-0,1047	0,0410	0,7371	0,0408	0,2457	0,0407	0,0000	0,0407	0,0398	2,2113
0,0000	-0,0662	0,0000	-0,0662	0,0000	-0,0662	0,0000	-0,0662	-0,0673	1,6616
0,1047	-0,1680	0,2387	-0,1677	0,0597	-0,1676	0,0000	-0,1676	-0,1689	0,7757
0,2094	-0,2489	0,1610	-0,2486	0,0402	-0,2485	0,0000	-0,2485	-0,2498	0,5231
0,3142	-0,3051	0,0984	-0,3049	0,0328	-0,3049	0,0328	-0,3048	-0,306	0,3937
0,4189	-0,3340	0,0599	-0,3339	0,0300	-0,3338	0,0000	-0,3338	-0,3345	0,2097
0,5236	-0,3333	0,0000	-0,3333	0,0000	-0,3333	0,0000	-0,3333	-0,3333	0,0000

де n тАУ кiлькiсть промiжкiв; x_i тАУ вузли сiтки ; y_i тАУ наближенi значення шуканоi функцii у вузлах;

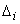Ва- вiдносна похибка у вiдсотках

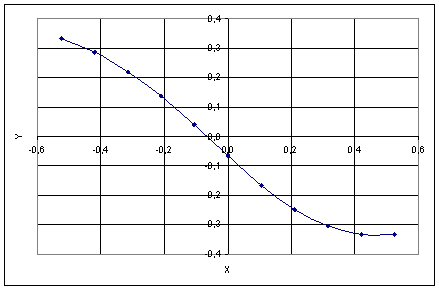
Рис.1 Графiк розвтАЩязку крайовоi задачи

Висновки

Висновки: за перiод проходження навчально-обчислювальноi практики я ознайомився з чисельними методами розвтАЩязання крайових задач зокрема з рiзницевим методом. Для iндивiдуального варiанту завдання був знайдений розвтАЩязок крайовоi задачi з заданою правою частиною. Розрахунок здiйснювався за допомогою програми на мовi Turbo Pascal. Рiзницевий метод виявився доволi простим в реалiзацii на алгоритмiчнiй мовi та дав швидку збiжнiсть.

Список використаноi лiтератури

1. Калиткин Н. Н. Численные методы. тАУ М.: Наука, 1978. тАУ 512 с.

2. Самарский А. А. Теория разностных схем. тАУ М.: Наука, 1989. тАУ 616 с.

3. Самарский А. А., Николаев Е. С. Методы решения сеточных уравнений. тАУ М.: Наука, 1978. тАУ 592 с.

4. Рапаков Г. Г., Ржеуцкая С. Ю. Программирование на языке Pascal. . тАУ СПб.: БХВ-Петербург, 2005. тАУ 480 с.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы