Метод вращений решения СЛАУ
Как утверждается в книге известного американского математика Валяха, 75% всех расчетных математических задач приходится на решение СЛАУ. Это не удивительно, так как математические модели тех или иных явлений или процессов либо сразу строятся как линейные алгебраические, либо сводятся к таковым посредством дискретизации и/или линеаризации. Поэтому трудно переоценить роль, которую играет выбор эффективного способа решения СЛАУ. Современная вычислительная математика располагает большим арсеналом методов, а математическое обеспечение ЭВМ тАУ многими пакетами прикладных программ, позволяющих решать различные возникающие на практике линейные системы. Чтобы ориентироваться среди методов и программ и в нужный момент сделать оптимальный выбор нужно разбираться в основе построений методов и алгоритмов, учитывающих специфику постановок задач, знать их сильные и слабые стороны и границы применимости.
1 Теоретический обзорматематический модель итерация погрешность
Все методы решения линейных алгебраических задач можно разбить на два класса: прямые и итерационные. Прямые методы тАУ это такие методы, которые приводят к решению за конечное число арифметических операций. Если операции реализуются точно, то и решение также будет точным (в связи с чем к классу прямых методов применяют название точные методы). Итерационные методы тАУ это методы в которых точное решение может быть получено лишь в результате бесконечного повторения единообразных действий.
Эффективность способов решения системы
 Ваили
Ваили
иначе, векторно-матричных уравнений Ах=f, где f=(f1, f2, тАж,fn)T тАУ вектор свободных членов и
х=( х1, х2, тАж,хn)T тАУ вектор неизвестных, а  ВатАУ вещественная n×n-матрица коэффициентов данной системы, во многом зависит от структуры и свойств матрицы А : размера, обусловленности, симметричности, заполненности и др.
ВатАУ вещественная n×n-матрица коэффициентов данной системы, во многом зависит от структуры и свойств матрицы А : размера, обусловленности, симметричности, заполненности и др.
Так размерность системы (т.е число n) является главным фактором, заставляющим вычислителей отвернуться от весьма привлекательных в теоретическом плане и приемлемых на практике при небольших n формул Крамера.
Рассмотрим один из самых распространенных методов решения СЛАУ тАУ метод Гаусса. Этот метод (который называют также методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Вычисления с помощью метода Гаусса состоят из двух основных этапов, называемых прямым ходом и обратным ходом. Прямой ход метода Гаусса заключается в последовательном исключении неизвестных из системы (1):

для преобразования её к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
Как и в методе Гаусса, цель прямого хода преобразований в этом методе тАУ приведение системы к треугольному виду последовательным обнулением поддиагональных элементов сначала первого столбца, затем второго и т.д.
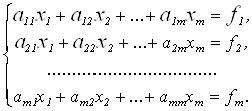
Пусть с1 и s1 тАУ некоторые отличные от нуля числа. Умножим первое уравнение исходной системы (1) на с1, второе на s1 и сложим их; полученным уравнением заменим первое уравнение системы. Затем первое уравнение исходной системы умножаем на тАУs1, второе тАУ на c1 и результатом их сложения заменим второе уравнение. Таким образом, первые два уравнения (1) заменяются уравнениями

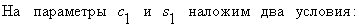

Отсюда 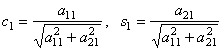 .
.
Эти числа можно интерпретировать как косинус и синус некоторого угла 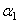 (отсюда название метод вращений, каждый шаг такого преобразования можно рассматривать как вращение расширенной матрицы системы в плоскости обнуляемого индекса).
(отсюда название метод вращений, каждый шаг такого преобразования можно рассматривать как вращение расширенной матрицы системы в плоскости обнуляемого индекса).
В результате преобразований получим систему
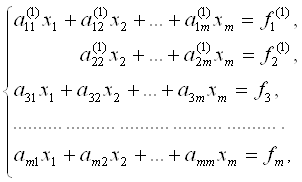
где
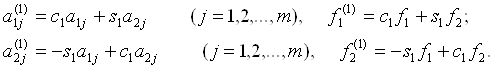
Далее первое уравнение системы заменяется новым, полученным сложением результатов умножения первого и третьего уравнений соотведлтственно на

а третье тАУ уравнением, полученным при сложении результатов умножения тех же уравнений соответственно на тАУs2 и с2. Получим систему
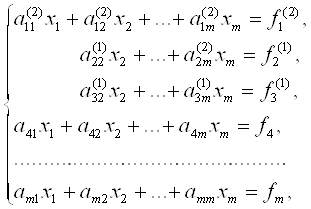
где
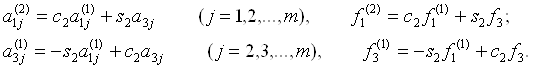
Выполнив преобразование m-1 раз, придем к системе
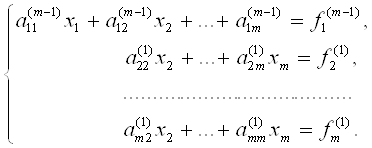
Вид полученной системы такой же, как после первого этапа преобразований методом Гаусса. Эта система обладает следующим свойством: длина любого вектора-столбца (эвклидова норма) расширенной матрицы остается такой же, как у исходной матрицы. Следовательно, при выполнении преобразований не наблюдается рост элементов.
Далее по этому же алгоритму преобразуется матрица

и т.д.
В результате m-1 этапов прямого хода система будет приведена к треугольному виду.
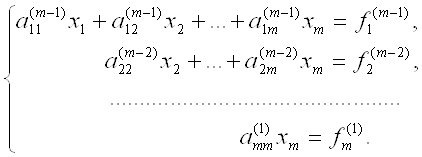
Нахождение неизвестных не отличается от обратного хода метода Гаусса.
Треугольная, точнее, трапециевидная структура последней системы позволяет последовательно одно за другим вычислять значения неизвестных, начиная с последнего:



Прямые методы часто приводят к точному решению СЛАУ при точном выполнении предусматриваемых соответствующими алгоритмами арифметических операций (без округлений).
Реальные же вычисления базируются на арифметике машинных (т.е. усеченных до определенного количества разрядов) чисел. Как отражается на результате решения системы подмена арифметики действительных чисел машинной арифметикой, зависит от самой решаемой системы, параметров применяемого компьютера и системы представления данных, способов реализации алгоритмов. В любом случае, практически вместо точного решения СЛАУ прямой метод дает приближенное решение*) (обозначим его х(0)). Подставив х(0) в выражение ξ:=f-Ax, называемое невязкой, по малости полученного вектора значения ξ(0)=f-Ax(0) можно с осторожностью судить о близости найденого решения x(0) к точному решению x. Если, напимер,
|| ξ(0)|| - недостаточно малая величина, то следует искать вектор-поправку p такой, что x(0)+р=х есть точное решение системы
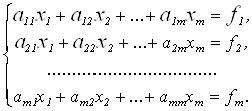 Ват.е. А(х(0)+р)=f.
Ват.е. А(х(0)+р)=f.
Последнее равносильно векторно матричному уравнению
Ар = ξ(0).
Таким образом, нахождение поправки сводится к решению такой же системы, как и
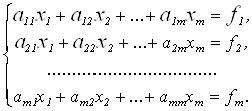 ,
,
где в качестве вектора свободных членов должен быть взят вектор невязок.
| trrr(a,f,x,m) | Функция, возвращающая матрицу невязок |
| prr(a,r,m) | Функция, возвращающая матрицу поправок |
| maxv(v,el) | Функция, возвращающая модуль максимального элемента вектора v |
| switchColumns(A,n1,n2,m) | Функция, возвращающая матрицу, полученную из А путем перестановки n1-ого и n2-ого столбцов |
| Podgotovka(A,m) | Функция, возвращающая 2 матрицы: матрицу, полученную из A перестановкой столбцов и пригодную для проведения вычислений; вектор, содержащий порядок следования неизвестных (1, 2,тАж n для x1, x2тАжxn соответственно) в уравнениях |
| rotation(a,f,m,e) | Функция, реализующая метод вращения. Возвращает 2 матрицы: неизвестных и поправок |
| a | Матрица коэффициентов |
| f | Матрица свободных членов |
| x | Матрица неизвестных |
| m | Количество неизвестных |
| e | Точность, с которой необходимо производить вычисления |
| | |
2.2 Листинг программы

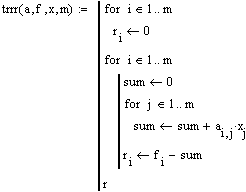
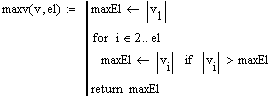
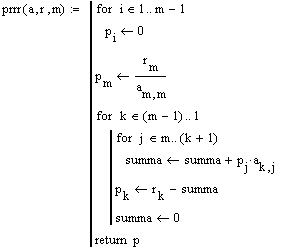
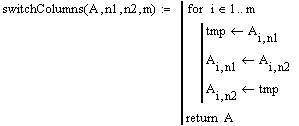


2.3 Пример.

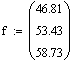
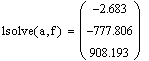
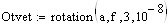
Подсчитаем матрицу неизвестных(Otvet1) и матрицу поправок(Otvet2)
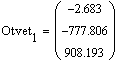
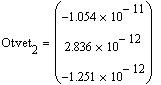
Для сравнения, погрешность метода Гаусса:
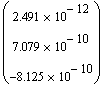
Таким образом, можно говорить о том, что, действительно, метод вращений более точен.
2.4 Сравнительная таблица
ЗаключениеВ данной работе был рассмотрен метод релаксации решения систем линейных алгебраических уравнений. Была подробно рассмотрена теоретическая часть, из которой выводятся различные формулы для реализации данного метода. А также было выполнено сравнение метода релаксации с методами простой итерации и Зейделя. Программная реализация выше описанных методов представлена в приложении А.
По результатам работы можно сделать следующие выводы. Во-первых, скорость сходимости метода релаксации превышает скорости сходимости методов простой итерации и Зейделя. Во-вторых, скорость сходимости напрямую зависит от выбора параметра релаксации. Таким образом, данный метод удобен для решения СЛАУ средней размерности.
Еще одно достоинство итерационного метода верхних релаксаций состоит в том, что при его реализации на ЭВМ алгоритм вычислений имеет простой вид и позволяет использовать всего один массив для неизвестного вектора.
Библиографический список1) Вержбицкий В. М. Основы численных методов: Учеб. пособие для вузов / В. М. Вержбицкий. - М. : Высш. шк. , 2002. - 840 с.
2) И.Г. Серебренникова, Г.М. Коринченко, Вычислительная математика. МГТУ им Г.И. Носова 2003г. 146с
3) Е. Волков.Численные методы. М.,1987, 248 с.
4) А. И. Плис, Н. А. Сливина. Лабораторный практикум по высшей математике. - М.: "Высшая школа", 1983.
5) Калиткин Н.Н. Численные методы. М.: Наука, 1978, 512 с.
6) Демидович Б.П., Марон И.А. Основы вычислительной математики. -М.: Наука, 1966 г., 664 стр.
7) Фадеев Д.К., Фадеева В.Н. Вычислительные методы линейной алгебры. М. Физматлит, 1960.
8) Воеводин В.В. Вычислительные основы линейной алгебры. - М.: Наука, 1977. - 304 с.
9) А. Самарский. Введение в численные методы. М.,1988, 270 с.
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы