Представление булевых функций в СКНФ
Курсовая работа
ВлПредставление булевых функций в СКНФВ»
В курсе дискретной математики изучаются функции, область определения которых тАУ дискретное множество. Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов.
Теоретическая часть
В теории дискретных функциональных систем булевой функцией называют функцию типа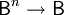 
, где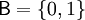 
тАУ булево множество, а n тАУ неотрицательное целое число, которое называют арностью или местностью функции. Элементы 0 (ноль) и 1 (единица) стандартно интерпретируют как истину и ложь, хотя в общем случае их смысл может быть любым. Элементы 
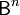называют булевыми векторами. В случае n = 0 булева функция превращается в булеву константу.
Каждая булева функция арности полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины . Число таких векторов равно 2n. Поскольку на каждом векторе функция может принимать значение либо 0, либо 1, количество всех n-арных булевых функций равно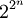 
. То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблиц. Такие таблицы носят название таблиц истинности и в общем случае имеют вид:
x1 | x2 | тАж | xn | f(x1, x2,тАж, x1) |
| 0 | 0 | тАж | 0 | f (0,0,тАж, 0) |
| 1 | 0 | тАж | 0 | f (1,0,тАж, 0) |
| 0 | 1 | тАж | 0 | f (0,1,тАж, 0) |
| 1 | 1 | тАж | 0 | f (1,1,тАж, 0) |
|
|
|
|
|
| 0 | 1 | тАж | 1 | f (0,1,тАж, 1) |
| 1 | 1 | тАж | 1 | f (1,1,тАж, 1) |
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы