Численные методы анализа

1. Численные методы решения систем линейных уравнений.

1.1 Заданная система

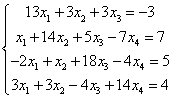
1.2 Метод Гаусса

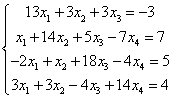ВаВа (1.1.)

Прямой ход

Нормируем первое уравнение системы, разделив все члены уравнения на его первый коэффициент при :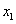

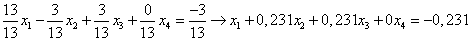ВаВаВаВаВаВаВаВа (1.2.)

Умножим нормированное уравнение (1.2) на коэффициенты при х₁ оставшихся уравнений системы (1.1).

(1.3.)

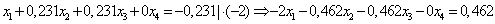ВаВаВаВаВаВа (1.4.)

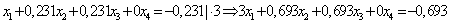ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.5.)

Вычтем полученные уравнения (1.3.), (1.4.), (1.5.) из второго, третьего и четвёртого уравнения системы (1.1.) соответственно, чтобы исключить из системы х₁:

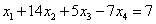
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.6.)

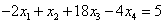
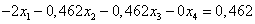ВаВаВаВа ВаВаВаВаВаВаВаВа (1.7.)

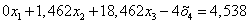
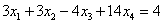
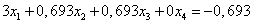ВаВаВаВаВа Ва(1.8.)

Получим новую систему уравнений:

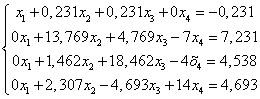ВаВаВа (1.9.)

Рассмотрим систему уравнений (1.9).

Решим систему уравнений без первого уравнения системы (1.9.).

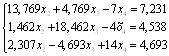ВаВаВа (1.10.)

Нормируем первое уравнение системы (1.10.), разделив все члены уравнения на коэффициент при :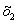

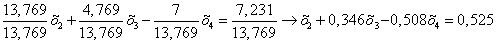ВаВаВа Ва(1.11.)

Умножаем нормированное уравнение (1.11.) на коэффициент при х₂ оставшихся уравнений:

Ва(1.12.)

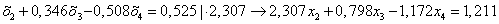ВаВаВа Ва(1.13.)

Вычтем полученные уравнения (1.12.), (1.13.) из второго и третьего уравнения системы (1.10.) соответственно, чтобы исключить из системы х₂:

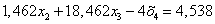
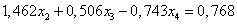ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.14.)

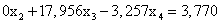
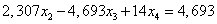
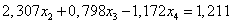ВаВаВаВаВаВаВаВаВа (1.15.)

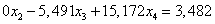
Получим новую систему уравнений:

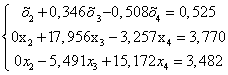ВаВаВаВаВаВаВаВаВаВа (1.16.)

Рассмотрим систему (1.16) без первого уравнения:

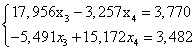ВаВаВаВаВаВаВа Ва(1.17.)

Нормируем первое уравнение системы (1.17.).

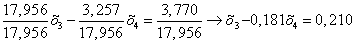ВаВаВаВаВаВаВаВаВаВаВаВаВа (1.18.)

Умножаем полученное уравнение (1.18.) на коэффициент при х₄ второго уравнения системы (1.17.):

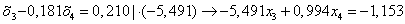ВаВаВа ВаВаВаВаВаВаВаВа (1.19.)

Вычтем полученное уравнение (1.19.) из второго уравнения системы (1.18.):

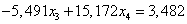
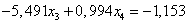(1.20.)

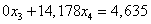
Получим новую систему линейных уравнений:

ВаВаВа Ва(1.21.)

Рассмотрим последнее уравнение системы (1.21.).

Нормируем данное уравнение:

ВаВаВаВаВаВаВаВаВаВа (1.22.)

В результате выполненных действий система (1.1.) приведена к треугольному виду:

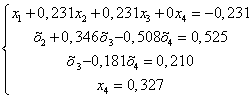ВаВаВаВаВа Ва(1.23.)

Обратный ход

x₄ = 0,327;

Найдём 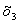Ваиз третьего уравнения системы (1.23.):

x₃ = 0,210+0,181В·0,327=0,269;

Найдём 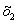Ваиз второго уравнения системы (1.23.):

x₂ = 0,525тАУ0,346В·0,269+0,508В·0,327 = 0,598;

Найдём 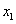Ваиз первого уравнения системы (1.23.):

x₁ = -0,231тАУ0,231В·0,598тАУ0,231В·0,269+0В·0,327 = -0,431

Решением системы линейных уравнений являются значения неизвестных:

Ответ: x₁ = -0,431;

x₂ = 0,598;

x₃ = 0,269;

x₄ = 0,327.

1.3 Метод простой итерации

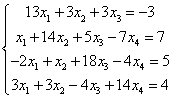
Выполним проверку на сходимость

|a₁₁|>|a₁₂|+|a₁₃|+|a₁₄| → |13|>|3|+|3|+|0|

|a₂₂|>|a₂₁|+|a₂₃|+|a₂₄| → |14|>|1|+|5|+|-7|

|a₃₃|>|a₃₁|+|a₃₂|+|a₃₄| → |18|>|-2|+|1|+|-4|

|a₄₄|>|a₄₁|+|a₄₂|+|a₄₃| → |14|>|3|+|3|+|-4|

Условия сходимости выполняются, следовательно, решение может быть найдено с определенной точностью за некоторое число итераций.

Вычислим значения неизвестных системы линейных алгебраических уравнений с точностью ε Ва0,001.

Примем за нулевое приближение неизвестных значения, равные нулю, т.е.

x₁⁽⁰⁾ = 0; x₂⁽⁰⁾ = 0; x₃⁽⁰⁾ = 0; x₄⁽⁰⁾ = 0;

Подставим полученные значения в итерационные формулы и вычислим значения неизвестных при первом приближении.

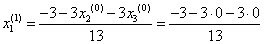= -0,231

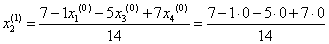= 0,500

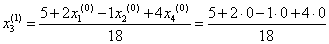= 0,278

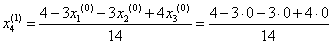= 0,286

Выполним проверку полученных значений:

|x₁⁽¹⁾-x₁⁽⁰⁾| = |-0,231тАУ0| = 0,231 Ваε тАУ нет

|x₂⁽¹⁾-x₂⁽⁰⁾| = |0,500тАУ0| = 0,500 Ваε тАУ нет

|x₃⁽¹⁾-x₃⁽⁰⁾| = |0,278тАУ0| = 0,278 Ваε тАУ нет

|x₄⁽¹⁾-x₄⁽⁰⁾| = |0,286тАУ0| = 0,286 Ваε тАУ нет

Выполним вторую итерацию.

Подставим значения неизвестных, полученные в первой итерации, в итерационные формулы и вычислим значения неизвестных при втором приближении.

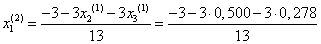= -0,410

= 0,560

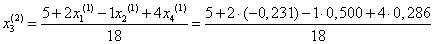= 0,288

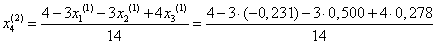= 0,308

Выполним проверку полученных значений:

|x₁⁽²⁾-x₁⁽¹⁾| = |-0,410+0,231| = 0,179 Ваε тАУ нет,

|x₂⁽²⁾-x₂⁽¹⁾| = |0,560тАУ0,500| = 0,060 Ваε тАУ нет,

|x₃⁽²⁾-x₃⁽¹⁾| = |0,288тАУ0,278| = 0,010 Ваε тАУ нет,

|x₄⁽²⁾-x₄⁽¹⁾| = |0,308тАУ0,286| = 0,022 Ваε тАУ нет.

Выполним третью итерацию.

Подставим значения, полученные во втором приближении, в итерационные формулы и вычислим значения неизвестных при третьем приближении.

= -0,427

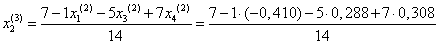= 0,580

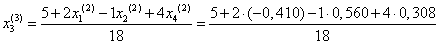= 0,270

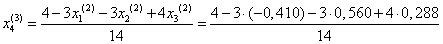= 0,336

Выполним проверку полученных значений:

|x₁⁽³⁾-x₁⁽²⁾| = |-0,427+0,410| = 0,017 Ваε тАУ нет,

|x₂⁽³⁾-x₂⁽²⁾| = |0,580+0,560| = 0,020 Ваε тАУ нет,

|x₃⁽³⁾-x₃⁽²⁾| = |0,270тАУ0,288| = 0,018 Ваε тАУ нет,

|x₄⁽³⁾-x₄⁽²⁾| = |0,336тАУ0,308| = 0,028 Ваε тАУ нет.

Выполним четвёртую итерацию.

Подставим значения, полученные в третьем приближении, в итерационные формулы и вычислим значения неизвестных при четвертом приближении.

= -0,427

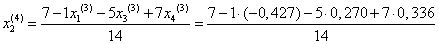= 0,602

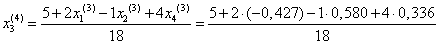= 0,273

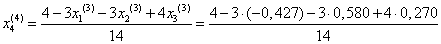= 0,330

Выполним проверку полученных значений:

|x₁⁽⁴⁾-x₁⁽³⁾| = |-0,427+0,427| = 0,000 Ваε тАУ да,

|x₂⁽⁴⁾-x₂⁽³⁾| = |0,602тАУ0,580| = 0,022 Ваε тАУ нет,

|x₃⁽⁴⁾-x₃⁽³⁾| = |0,273тАУ0,270| = 0,003 Ваε тАУ нет,

|x₄⁽⁴⁾-x₄⁽³⁾| = |0,330тАУ0,336| = 0,006 Ваε тАУ нет.

Выполним пятую итерацию.

Подставим значения, полученные в четвертом приближении, в итерационные формулы и вычислим значения неизвестных при пятом приближении.

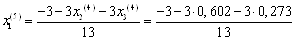= -0,433

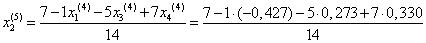= 0,598

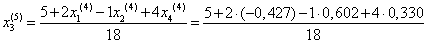= 0,270

= 0,326

Выполним проверку полученных значений:

|x₁⁽⁵⁾-x₁⁽⁴⁾| = |-0,433+0,427| = 0,006 Ваε тАУ нет,

|x₂⁽⁵⁾-x₂⁽⁴⁾| = |0,598тАУ0,602| = 0,004 Ваε тАУ нет,

|x₃⁽⁵⁾-x₃⁽⁴⁾| = |0,270тАУ0,273| = 0,003 Ваε тАУ нет,

|x₄⁽⁵⁾-x₄⁽⁴⁾| = |0,326тАУ0,330| = 0,004 Ваε тАУ нет.

Выполним шестую итерацию.

Подставим значения, полученные в пятом приближении, в итерационные формулы и вычислим значения неизвестных при шестом приближении.

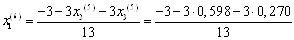= -0,431

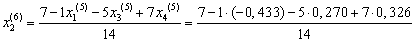= 0,597

= 0,269

= 0,327

Выполним проверку полученных значений:

|x₁⁽⁶⁾-x₁⁽⁵⁾| = |-0,431+0,433| = 0,002 Ваε тАУ нет,

|x₂⁽⁶⁾-x₂⁽⁵⁾| = |0,597тАУ0,598| = 0,001 Ваε тАУ да,

|x₃⁽⁶⁾-x₃⁽⁵⁾| = |0,269тАУ0,270| = 0,001 Ваε тАУ да,

|x₄⁽⁶⁾-x₄⁽⁵⁾| = |0,327тАУ0,326| = 0,001 Ваε тАУ да.

Выполним седьмую итерацию.

Подставим значения, полученные в шестом приближении, в итерационные формулы и вычислим значения неизвестных при седьмом приближении.

= -0,431

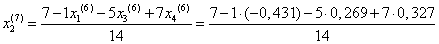= 0,598

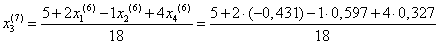= 0,269

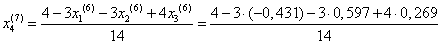= 0,327

Выполним проверку полученных значений:

|x₁⁽⁷⁾-x₁⁽⁶⁾| = |-0,431+0,431| = 0,000 Ваε тАУ да,

|x₂⁽⁷⁾-x₂⁽⁶⁾| = |0,598тАУ0,597| = 0,001 Ваε тАУ да,

|x₃⁽⁷⁾-x₃⁽⁶⁾| = |0,269тАУ0,269| = 0,000 Ваε тАУ да,

|x₄⁽⁷⁾-x₄⁽⁶⁾| = |0,327тАУ0,327| = 0,000 Ваε тАУ да.

Необходимая точность достигается в седьмой итерации.

Ответ: ВаВаВаВаВа х₁ = -0,431,

х₂ = 0,598,

х₃ = 0,269,

х₄ = 0,327.

1.4 Метод Зейделя

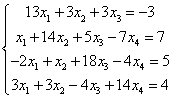
Условия сходимости было проверено выше, оно выполняется.

Точность вычисления ε Ва0,001.

Примем за нулевое приближение неизвестных значений, равные нулю.

x₁⁽⁰⁾ = x₂⁽⁰⁾ = x₃⁽⁰⁾ = x₄⁽⁰⁾ = 0;

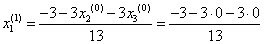= -0,231

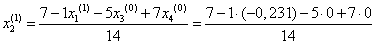= 0,517

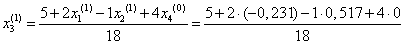= 0,223

= 0,288

Выполним проверку полученных значений:

|x₁⁽¹⁾-x₁⁽⁰⁾| = |-0,231тАУ0| = 0,231 Ваε тАУ нет

|x₂⁽¹⁾-x₂⁽⁰⁾| = |0,517тАУ0| = 0,517 Ваε тАУ нет

|x₃⁽¹⁾-x₃⁽⁰⁾| = |0,223тАУ0| = 0,223 Ваε тАУ нет

|x₄⁽¹⁾-x₄⁽⁰⁾| = |0,288тАУ0| = 0,288 Ваε тАУ нет

Выполним вторую итерацию.

Подставим значения, полученные в первом приближении, в итерационные формулы и вычислим значения неизвестных при втором приближении.

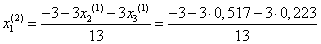= -0,402

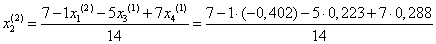= 0,593

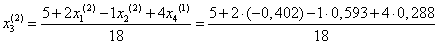= 0,264

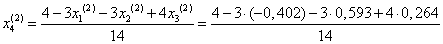= 0,320

Выполним проверку полученных значений:

|x₁⁽²⁾-x₁⁽¹⁾| = |-0,402+0,231| = 0,171 Ваε тАУ нет,

|x₂⁽²⁾-x₂⁽¹⁾| = |0,593тАУ0,517| = 0,076 Ваε тАУ нет,

|x₃⁽²⁾-x₃⁽¹⁾| = |0,264тАУ0,223| = 0,041 Ваε тАУ нет,

|x₄⁽²⁾-x₄⁽¹⁾| = |0,320тАУ0,288| = 0,032 Ваε тАУ нет.

Выполним третью итерацию.

= -0,429

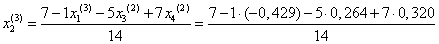= 0,596

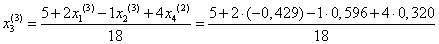= 0,268

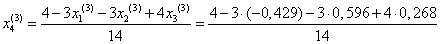= 0,326

Выполним проверку полученных значений:

|x₁⁽³⁾-x₁⁽²⁾| = |-0,429+0,402| = 0,027 Ваε тАУ нет,

|x₂⁽³⁾-x₂⁽²⁾| = |0,596тАУ0,593| = 0,003 Ваε тАУ нет,

|x₃⁽³⁾-x₃⁽²⁾| = |0,268тАУ0,264| = 0,004 Ваε тАУ нет,

|x₄⁽³⁾-x₄⁽²⁾| = |0,326тАУ0,320| = 0,006 Ваε тАУ нет.

Выполним четвёртую итерацию.

Подставим значения, полученные в третьем приближении, в итерационные формулы и вычислим значения неизвестных при четвёртом приближении.

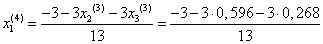= -0,430

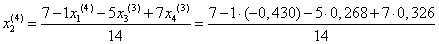= 0,598

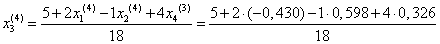= 0,269

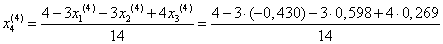= 0,327

Выполним проверку полученных значений:

|x₁⁽⁴⁾-x₁⁽³⁾| = |-0,430+0,429| = 0,01 Ваε тАУ да,

|x₂⁽⁴⁾-x₂⁽³⁾| = |0,598тАУ0,596| = 0,002 Ваε тАУ нет,

|x₃⁽⁴⁾-x₃⁽³⁾| = |0,269тАУ0,268| = 0,001 Ваε тАУ да,

|x₄⁽⁴⁾-x₄⁽³⁾| = |0,327тАУ0,326| = 0,001 Ваε тАУ да.

Выполним пятую итерацию.

Подставим значения, полученные в четвёртом приближении, в итерационные формулы и вычислим значения неизвестных при пятом приближении.

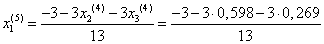= -0,431

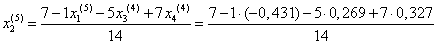= 0,598

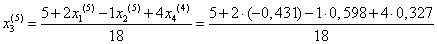= 0,269

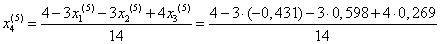= 0,327

Выполним проверку полученных значений:

|x₁⁽⁵⁾-x₁⁽⁴⁾| = |-0,431+0,430| = 0,001 Ваε тАУ да,

|x₂⁽⁵⁾-x₂⁽⁴⁾| = |0,598тАУ0,598| = 0,000 Ваε тАУ да,

|x₃⁽⁵⁾-x₃⁽⁴⁾| = |0,269тАУ0,269| = 0,000 Ваε тАУ да,

|x₄⁽⁵⁾-x₄⁽⁴⁾| = |0,327тАУ0,327| = 0,000 Ваε тАУ да.

Необходимая точность достигается в пятой итерации.

Ответ: ВаВаВаВаВа х₁ = -0,431,

х₂ = 0,598,

х₃ = 0,269,

х₄ = 0,327.

2. Численные методы аппроксимации и интерполяции функций

2.1 Задание

Найти интерполяционный полином второго порядка

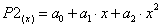
методом неопределённых коэффициентов, используя данные нулевого, второго и четвёртого опытов.

Найти аппроксимирующий полином первого порядка

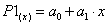
методом наименьших квадратов.

Исходные данные

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 0ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 1ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 2ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 3 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 4

x_i	0,1	0,3	0,5	0,8	1
y_i	0,3	0,55	0,65	0,4	0,25

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы