Модели и методы принятия решений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Курсовая работа
Модели и методы принятия решений
Выполнила: Токарева О.П.
Заочная форма обучения
Курс V
Специальность 210100
№ зачетной книжки 602654
Проверил: Цыганов Ю.К.
Москва
2008
Задание
на курсовую работу по дисциплине ВлМодели и методы принятия решенийВ»
Вариант 4
Задача 1.
Решить графоаналитическим методом.
min j (X) = тАУ 3x1 тАУ 2x2
при 2x1 + x2 ³ 2
x1 + x2 £ 3
тАУ x1 + x2 ³ 1
X ³ 0
Задача 2.
В· Найти экстремумы методом множителей Лагранжа.
В· Решение проиллюстрировать графически.
extr j (X) = x12 + x22
при x12 + x22 тАУ 9x2 + 4,25 = 0
Задача 3.
В· Решить на основе условий Куна-Таккера.
В· Решение проиллюстрировать графически.
extr j (X) = x1x2
при 6x1 + 4x2 ³ 12
2x1 + 3x2 £ 24
тАУ 3x1 + 4x2 £ 12
Задача 4.
В· Получить выражение расширенной целевой функции (РЦФ) и составить блок-схему алгоритма численного решения задачи методом штрафных функций в сочетании с одним из методов безусловной минимизации.
В· Решить задачу средствами MS Excel.
В· Решение проиллюстрировать графически.
max j (X) = 2x1 + 4x2 тАУ x12 тАУ 2x22
при x1 + 2x2 £ 8
2x1 тАУ x2 £ 12
X ³ 0
Задача 1
Решить графоаналитическим методом.
min j (X) = тАУ 3x1 тАУ 2x2
при 2x1 + x2 ³ 2
x1 + x2 £ 3
тАУ x1 + x2 ³ 1
X ³ 0
Решение:
Построим линии ограничений:
Примем: 2х1+х2=2ВаВаВаВаВаВаВаВаВаВаВаВаВаВа (a)
х1+х2=3ВаВаВаВаВаВаВаВаВаВаВаВаВа (b)
-х1+х2=1ВаВаВаВаВаВаВаВаВаВаВаВа (c)
экстремум функция минимизация алгоритм
Получаем три прямые a, b и c, которые пересекаются и образуют треугольник соответствующий области которая соответствует первым трем ограничениям, добавляя четвертое ограничение получаем четырехугольник ABCD тАУ допустимая область значений, в которой надо искать минимум (на рисунке эта область не заштрихована).
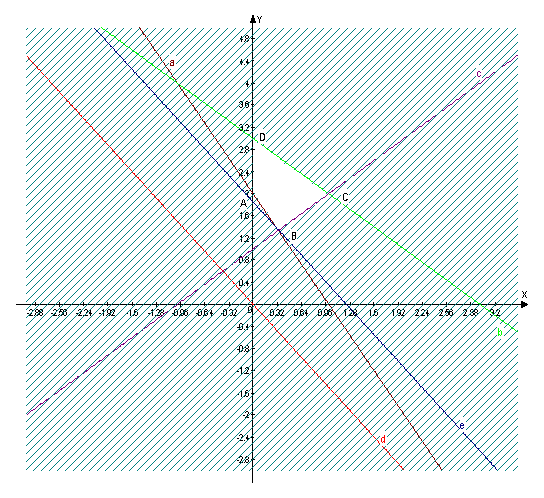
Рис. 1
Примем целевую функцию равной нулю (красная линия d) тогда градиент имеет координаты (-3;-2). Для того, чтобы найти минимум целевой функции будем перемещать график линии d параллельно самой себе в направлении антиградиента до входа ее в область ограничений. Точка в которой область войдет в допустимую область и будет искомой точкой минимума целевой функции. Это точка В(0,33 ; 1,33). При этом целевая функция будет иметь значение:
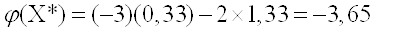
Темно-синяя линия на рисунке (е).
Задача 2.
В· Найти экстремумы методом множителей Лагранжа.
В· Решение проиллюстрировать графически.
extr j (X) = x12 + x22
при x12 + x22 тАУ 9x2 + 4,25 = 0
Решение:
Составим функцию Лагранжа
h(X)=x12 + x22 - 9x2 + 4,25=0
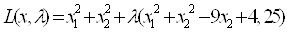
Составим систему уравнений из частных производных и приравняем их к нулю:

Решим данную систему уравнений:
Разложим на множители 1 уравнение системы:
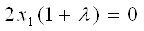
Предположим, что 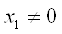 , тогда
, тогда 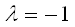 . Подставим во второе уравнение:
. Подставим во второе уравнение:
2x2 - 2x2 + 9 = 0
9 = 0 не верно, следовательно принимаем, что
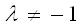 , а
, а 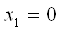
Подставляем 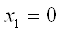 Вав третье уравнение:
Вав третье уравнение:

Решая это квадратное уравнение получаем, что

Подставляем эти значения во второе уравнение:
1.Подставим первый корень  , получаем
, получаем

2. Подставим второй корень 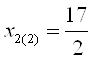 , получаем
, получаем
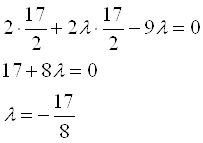
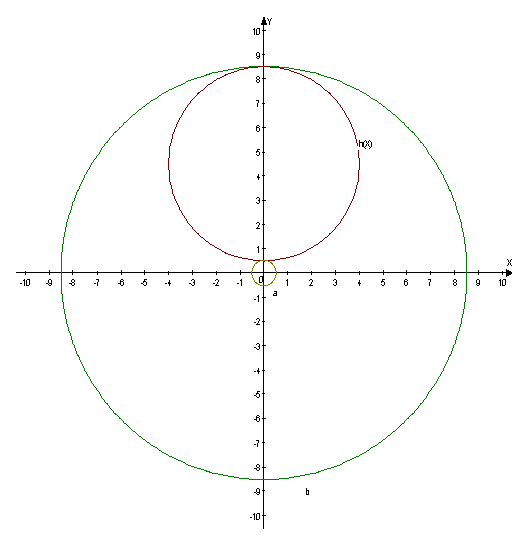
( X*,λ*) N | X1* | X2* | λ* | φ(X*) | Примечание |
| 1 | 0 | 
| 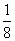
| 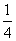
| Min |
| 2 | 0 | 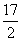
| 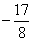
| 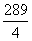
| Max |
 - кривая a (окружность)
- кривая a (окружность)
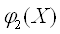 - кривая b (окружность)
- кривая b (окружность)
Задача 3
В· Решить на основе условий Куна-Таккера.
В· Решение проиллюстрировать графически.
extr j (X) = x1x2
при 6x1 + 4x2 ³ 12
2x1 + 3x2 £ 24
тАУ 3x1 + 4x2 £ 12
Решение:
Решим задачу на основе условий Куна-Таккера.
Составим функцию Лагранжа:
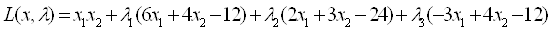
Составим систему уравнений из частных производных и приравняем их к нулю:

Решим данную систему уравнений:
1.Предположим, что , тогда из уравнения 5 получим:
, тогда из уравнения 5 получим:
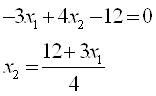
Предположим, что 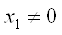 ,
,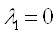 ,
,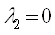 , тогда из уравнения 1 получим:
, тогда из уравнения 1 получим:
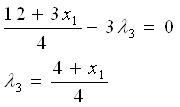
Пусть 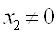 , тогда из уравнения 2 получаем:
, тогда из уравнения 2 получаем:
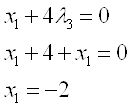
Это решение не удовлетворяет условиям задачи: (Х≥0)
2.Предположим, что 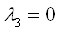 и
и 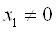 , тогда из уравнения 1 получим:
, тогда из уравнения 1 получим:
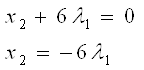
Предположим, что 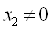 ,
, 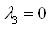 ,
, 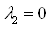 , выразим из второго уравнения
, выразим из второго уравнения 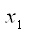 :
:
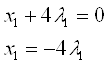
Подставим в 3 уравнение:
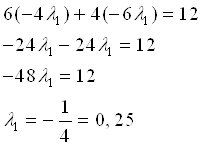
Получаем: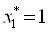 ,
,  ,
, 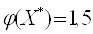
В этой точке функция 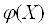 Варавна минимальному значению
Варавна минимальному значению
3. Предположим, что 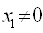 ,
, 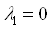 Ваи
Ваи 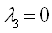 , тогда из второго уравнения получим:
, тогда из второго уравнения получим:
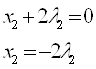
Предположим, что 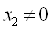 ,
,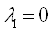 и
и 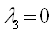 , тогда из второго уравнения следует:
, тогда из второго уравнения следует:

Подставим в четвертое уравнение:
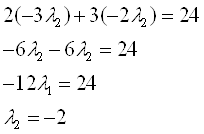
Получаем: 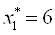 ,
, 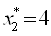 ,
, 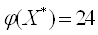
В этой точке функция 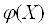 имеет максимальное значение:
имеет максимальное значение:
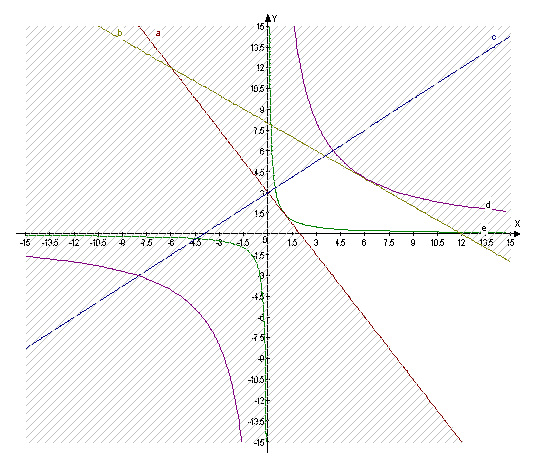
X* N | X1* | X2* | φ(X*) | Примечание |
| 1 | 1 | 1,5 | 1,5 | Min |
| 2 | 6 | 4 | 24 | Max |
Прямая а соответствует графику функции 6х1+4х2=12
Прямая b тАУ графику функции 2х1+3х2=24
Прямая с тАУ графику функции -3х1+4х2=12
Прямая d тАУ графику функции 
Прямая е тАУ графику функции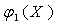
Задача 4
В· Получить выражение расширенной целевой функции (РЦФ) и составить блок-схему алгоритма численного решения задачи методом штрафных функций в сочетании с одним из методов безусловной минимизации.
В· Решить задачу средствами MS Excel.
В· Решение проиллюстрировать графически.
max j (X) = 2x1 + 4x2 тАУ x12 тАУ 2x22
при x1 + 2x2 £ 8
2x1 тАУ x2 £ 12
X ³ 0
Решение:
1. Найдем выражение вектор функции системы:
Составим функцию Лагранжа:
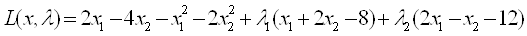
Вектор функция системы:

2. Составим матрицу Якоби
 =
=
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы
Анализ эмпирического распределения