Определение законов распределения и числовых характеристик случайной величины на основе опытных данных
Самарский государственный аэрокосмический университет имени академика С.П.Королева Кафедра высшей математики
Расчетно-пояснительная записка к курсовой работе по математике
г. Самара
Определение законов распределения и числовых характеристик случайной величины на основе опытных данных
Задание
В протокол внесено n=100 измерений случайной величины Х.
1. По выборке построить статистический ряд и гистограмму.
2. Найти статистическую функцию распределения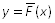 
и построить её график.
3. Вычислить числовые характеристики статистического ряда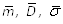 
.
4. Выровнять полученное распределение с помощью нормального закона.
Построить график теоретической кривой распределения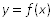 
в одной системе координат с гистограммой.
Построить график теоретической функции распределения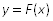 
в одной системе координат с графиком функции.
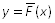5. Найти доверительный интервал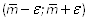
, в котором находится точное значение математического ожидания m случайной величины Х с доверительной вероятностью 
.
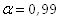6. С помощью критерия согласия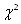 
проверить согласованность статистического и выбранного теоретического (нормального) распределения.
Генеральная совокупность и выборка, статистический ряд и гистограмма
Генеральной совокупностью-называется совокупность всех подлежащих изучению объектов или возможных результатов всех наблюдений, производимых в одинаковых условиях над одним объектом.
Выборочной совокупностью или выборкой называется совокупность объектов или результатов наблюдения над объектом, отобранных случайным образом из генеральной совокупности.
Объемом выборки называется число объектов или наблюдений в выборке.
Конкретные значения выборки называются наблюдаемыми значениями случайной величины Х. Наблюдаемые значения заносятся в протокол. Протокол представляет собой таблицу. Составленный протокол является первичной формой записи обработки полученного материала. Для получения достоверных, надежных выводов выборка должна быть достаточно представительной по объему. Большая выборка тАУ это неупорядоченное множество чисел. Для исследования выборку приводят к наглядному упорядоченному виду. Для этого в протоколе находят наибольшее и наименьшее значения случайной величины. Выборка, отсортированная по возрастанию, приведена в таблице 1.
Таблица 1. Протокол
| -8,66 | -5,49 | -4,11 | -3,48 | -2,9 | -2,32 | -1,82 | -1,09 | -0,44 | 0,64 |
| -8,31 | -4,71 | -3,92 | -3,41 | -2,85 | -2,31 | -1,82 | -1,01 | -0,43 | 0,71 |
| -8,23 | -4,68 | -3,85 | -3,33 | -2,83 | -2,29 | -1,8 | -0,99 | -0,43 | 0,73 |
| -7,67 | -4,6 | -3,85 | -3,25 | -2,77 | -2,27 | -1,77 | -0,95 | -0,31 | 0,99 |
| -6,64 | -4,43 | -3,81 | -3,08 | -2,72 | -2,25 | -1,73 | -0,89 | -0,3 | 1,03 |
| -6,6 | -4,38 | -3,8 | -3,07 | -2,67 | -2,19 | -1,38 | -0,7 | 0,04 | 1,05 |
| -6,22 | -4,38 | -3,77 | -3,01 | -2,6 | -2,15 | -1,32 | -0,56 | 0,08 | 1,13 |
| -5,87 | -4,25 | -3,73 | -3,01 | -2,49 | -2,09 | -1,3 | -0,51 | 0,15 | 1,76 |
| -5,74 | -4,18 | -3,59 | -2,99 | -2,37 | -2,01 | -1,28 | -0,49 | 0,26 | 2,95 |
| -5,68 | -4,14 | -3,49 | -2,98 | -2,33 | -1,91 | -1,24 | -0,48 | 0,53 | 4,42 |
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Автокорреляционная функция. Примеры расчётов
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы
Анализ эмпирического распределения