Похiднi та диференцiали функцii багатьох змiнних

ПОХРЖДНРЖ ТА ДИФЕРЕНЦРЖАЛИ ФУНКЦРЖРЗ БАГАТЬОХ ЗМРЖННИХ

1 Частиннi похiднi

Нехай функцiя Вавизначена в деякому околi точки .
Надамо змiннiй x приросту, залишаючи змiнну Ванезмiнною, так, щоб точка Ваналежала заданому околу.

Величина

називаiться частинним приростом функцii Ваза змiнною x.

Аналогiчно вводиться частинний прирiст Вафункцii за змiнною:

.

Якщо iснуi границя

,

то вона називаiться частинною похiдною функцii Вав точцi Ваза змiнною x i позначаiться одним iз таких символiв:

.

Аналогiчно частинна похiдна функцii за Вавизначаiться як границя

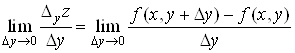
i позначаiться одним iз символiв:

.

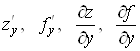Згiдно з означенням при знаходженнi частинноi похiдноi Ваобчислюють звичайну похiдну функцii однiii змiнноi x, вважаючи змiнну Васталою, а при знаходженнi похiдноi Васталою вважаiться змiнна x. Тому частиннi похiднi знаходять за формулами i правилами обчислення похiдних функцiй однiii змiнноi.

Частинна похiдна Ва(або) характеризуi швидкiсть змiни функцii в напрямi осi (або).

ЗтАЩясуiмо геометричний змiст частинних похiдних функцii двох змiнних. Графiком функцii Ваi деяка поверхня (рис 1). Графiком функцii Ваi лiнiя перетину цiii поверхнi з площиною. Виходячи з геометричного змiсту похiдноi для функцii однiii змiнноi, отримаiмо, що, детАУ кут мiж вiссю Ваi дотичною, проведеною до кривоi Вав точцi. Аналогiчно.

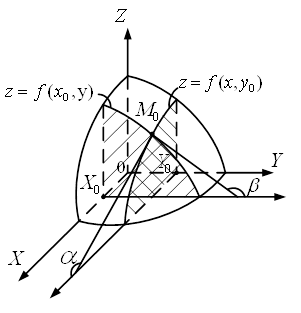
Рисунок 1 тАУ Геометричний змiст частинних похiдних

Для функцii Ваn змiнних можна знайти n частинних похiдних:

,

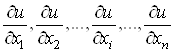де

,

.

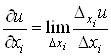Щоб знайти частинну похiдну, необхiдно взяти звичайну похiдну функцii Ваза змiнною, вважаючи решту змiнних сталими.

Якщо функцiя Вазадана в областi Ваi маi частиннi похiднi Вав усiх точках, то цi похiднi можна розглядати як новi функцii, заданi в областi.

Якщо iснуi частинна похiдна за x вiд функцii, то ii називають частинною похiдною другого порядку вiд функцii Ваза змiнною x i позначають Ваабо .

Таким чином, за означенням

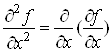або.

Якщо iснуi частинна похiдна вiд функцii Ваза змiнною, то цю похiдну називають мiшаною частинною похiдною другого порядку вiд функцii i позначають, або.

Отже, за означенням

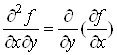або .

Для функцii двох змiнних Ваможна розглядати чотири похiднi другого порядку:

.

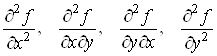Якщо iснують частиннi похiднi вiд частинних похiдних другого порядку, то iх називають частинними похiдними третього порядку функцii, iх вiсiм:

.

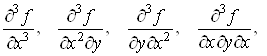
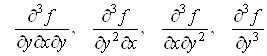Виникаi запитання: чи залежить результат диференцiювання вiд порядку диференцiювання? РЖнакше кажучи, чи будуть рiвними мiж собою мiшанi похiднi, якщо вони взятi за одними i тими самими змiнними, одне й те саме число разiв, але в рiзному порядку? Наприклад, чи дорiвнюють одна однiй похiднi

i Ваабо 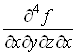Ваi?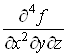

У загальному випадку вiдповiдь на це запитання негативна.

Проте справедлива теорема, яку вперше довiв К.Г.Шварц.

Теорема (про мiшанi похiднi).Якщо функцiя визначена разом iз своiми похiдними Вав деякому околi точки , причому похiднi Вата Ванеперервнi в точцi, то в цiй точцi

.

Аналогiчна теорема справедлива для будь-яких неперервних мiшаних похiдних, якi вiдрiзняються мiж собою лише порядком диференцiювання.

2 Диференцiйованiсть функцii

похiдна диференцiал функцiя змiнна

Нехай функцiя Вавизначена в деякому околi точки. Виберемо прирости Ваi Ватак, щоб точка Ваналежала розглядуваному околу i знайдемо повний прирiст функцii в точцi:

.

Функцiя Ваназиваiться диференцiйовною в точцi М, якщо ii повний прирiст в цiй точцi можна подати у виглядi

,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)

де Вата ВатАУ дiйснi числа, якi не залежать вiд Вата , ВатАУ нескiнченно малi при Ваi Вафункцii.

Вiдомо, що коли функцiя однiii змiнноi диференцiйовна в деякiй точцi, то вона в цiй точцi неперервна i маi похiдну. Перенесемо цi властивостi на функцii двох змiнних.

Теорема 1 (неперервнiсть диференцiйовноi функцii).

Якщо функцiя Вадиференцiйовна в точцi М, то вона неперервна в цiй точцi.

Доведення

Якщо функцiя диференцiйовна в точцi М, то з рiвностi (1) випливаi, що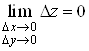. Це означаi, що функцiя неперервна в точцi М.

Теорема 2 (iснування частинних похiдних диференцiйовноi функцii). Якщо функцiя Вадиференцiйовна в точцi , то вона маi в цiй точцi похiднi Вата Ваi.

Доведення

Оскiльки Вадиференцiйовна в точцi,то справджуiться рiвнiсть (1). Поклавши в нiй, отримаiмо,

.

Подiлимо обидвi частини цiii рiвностi на Ваi перейдемо до границi при:

.

Отже, в точцi Ваiснуi частинна похiдна. Аналогiчно доводиться, що в точцi Ваiснуi частинна похiдна.

Твердження, оберненi до теорем 1 i 2, взагалi кажучи, неправильнi, тобто iз неперервностi функцii Ваабо iснування ii частинних похiдних ще не випливаi диференцiйовнiсть. Наприклад, функцiя Ванеперервна в точцi, але не диференцiйовна в цiй точцi. Справдi, границi

не iснуi, тому не iснуi й похiдноi. Аналогiчно впевнюiмося, що не iснуi також похiдноi. Оскiльки задана функцiя в точцi Ване маi частинних похiдних, то вона в цiй точцi не диференцiйовна.

Бiльш того, вiдомо приклади функцiй, якi i неперервними в деяких точках i мають в них частиннi похiднi, але не i в цих точках диференцiйовними.

Теорема 3 (достатнi умови диференцiйовностi ).

Якщо функцiя Вамаi частиннi похiднi в деякому околi точки i цi похiднi неперервнi в точцi М, то функцiя Вадиференцiйовна в точцi М.

Доведення

Надамо змiнним x i Ваприростiв , таких, щоб точка Ваналежала даному околу точки . Повний прирiст функцii Вазапишемо у виглядi

.ВаВаВа (2)

Вираз у перших квадратних дужках рiвностi (2) можна розглядати як прирiст функцii однiii змiнноi x, а в других тАУ як прирiст функцii змiнноi . Оскiльки дана функцiя маi частиннi похiднi, то за теоремою Лагранжа отримаiмо:

.

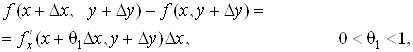
Похiднi Вата Ванеперервнi в точцi М, тому

,

.

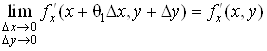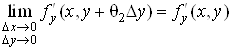Звiдси випливаi, що

,

,

де, ВатАУ нескiнченно малi функцii при Ваi.

Пiдставляючи цi вирази у рiвнiсть (2), знаходимо

, а це й означаi, що функцiя Вадиференцiйовна в точцi.

З теорем 2 i 3 випливаi такий наслiдок: щоб функцiя Вабула диференцiйовною в точцi, необхiдно, щоб вона мала в цiй точцi частиннi похiднi, i достатньо, щоб вона мала в цiй точцi неперервнi частиннi похiднi.

Зазначимо, що для функцii однiii змiнноi iснування похiдноi Вав точцi Ваi необхiдною i достатньою умовою ii диференцiйовностi в цiй точцi.

3 Повний диференцiал функцii та його застосування до обчислення функцiй i похибок. Диференцiали вищих порядкiв

Нагадаiмо, що коли функцiя Вадиференцiйовна в точцi, то ii повний прирiст у цiй точцi можна подати у виглядi

,

де Ваi Вапри.

Повним диференцiалом Вадиференцiйовноi в точцi Вафункцii Ваназиваiться лiнiйна вiдносно Вата Вачастина повного приросту цiii функцii в точцi M, тобто

.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)

Диференцiалами незалежних змiнних x та Ваназвемо прирости цих змiнних. Тодi з урахуванням теореми 2 рiвнiсть (3) можна записати так:

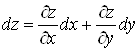.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)

Аналогiчна формула маi мiсце для диференцiйовноi функцii трьох змiнних:

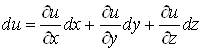.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)

З формул (4) i (5) може здатися, що повний диференцiал Ваiснуватиме у кожнiй точцi, в якiй iснують частиннi похiднi. Але це не так. Згiдно з означенням, повний диференцiал можна розглядати лише стосовно диференцiйовноi функцii.

Теореми та формули для диференцiалiв функцii однiii змiнноi повнiстю зберiгаються i для диференцiалiв функцiй двох, трьох i т.д. змiнних . Так, незалежно вiд того, вiд яких аргументiв залежать функцii u i , завжди справедливi рiвностi

Покажемо, що рiзниця мiж повним приростом Ваi диференцiалом Вапри Ваi Ваi нескiнченно мала величина вищого порядку, нiж величина.

Дiйсно, з формул (1) i (3) маiмо

,

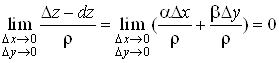оскiльки функцii ВатАУ нескiнченно малi при, , а Вата ВатАУ обмеженi функцii:

.

Отже, рiзниця ВатАУ нескiнченно мала величина вищого порядку, нiж. Тому повний диференцiал називають також головною частиною повного приросту диференцiйовноi функцii. При цьому виконуiться наближена рiвнiсть Ваабо

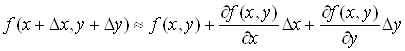.ВаВаВаВаВаВаВаВаВаВаВа (6)

Ця рiвнiсть тим точнiша, чим менша величина. Рiвнiсть (6) широко використовуiться у наближених обчисленнях, оскiльки диференцiал функцii обчислюiться простiше, нiж повний прирiст.

Покажемо, як за допомогою диференцiала можна оцiнити похибку в обчисленнях.

Нехай задана диференцiйовна функцiя, незалежнi змiннi якоi вимiрянi з точнiстю. Потрiбно знайти похибку, з якою обчислюiться u.

Природно вважати, що ця похибка дорiвнюi величинi

.

Для малих значень Вамаiмо

,

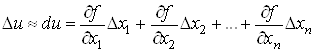звiдки

.

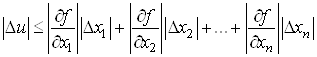Якщо через Вапозначити максимальну абсолютну похибку змiнноi , то можна отримати значення максимальноi абсолютноi похибки Вафункцii :

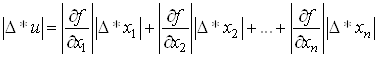.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (7)

Щоб оцiнити максимальну вiдносну похибку функцii u, подiлимо обидвi частини рiвностi (7) на:

.

Оскiльки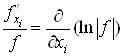, то

,

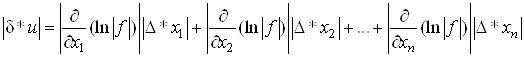або

,

тобто максимальна вiдносна похибка функцii дорiвнюi максимальнiй абсолютнiй похибцi ii логарифма.

Введемо поняття диференцiала вищого порядку.

Нехай Вафункцiя незалежних змiнних ,. Повний диференцiал цiii функцii, знайдений за формулою (3), називають ще диференцiалом
першого порядку. Диференцiал другого порядку визначають за формулою

.

Тодi, якщо функцiя Вамаi неперервнi частиннi похiднi, то

,

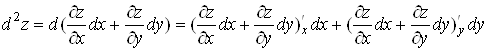звiдки

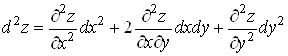.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (8)

Символiчно це записують так:

.

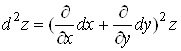Аналогiчно можна отримати формулу для диференцiала третього порядку:

.

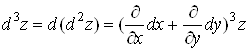Застосовуючи метод математичноi iндукцii, можна отримати формулу для диференцiала n-го порядку:

.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (9)

Зазначимо, що формула (9) справедлива лише для випадку, коли змiннi x i Вафункцii Ваi незалежними змiнними.

4 Похiдна складеноi функцii. Повна похiдна. РЖнварiантнiсть форми повного диференцiала

Нехай ВатАУ функцiя двох змiнних Вата , кожна з яких, у свою чергу, i функцiiю незалежноi змiнноi :

тодi функцiя Ваi складеною функцiiю змiнноi .

Теорема. Якщо функцii Вадиференцiйовнi в точцi , а функцiя Вадиференцiйовна в точцi , то складена функцiя Ватакож диференцiйовна в точцi . Похiдну цiii функцii знаходять за формулою

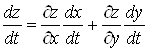.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (10)

Доведення

За умовою теореми ,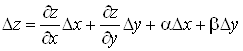

де Вата Вапри,.

Подiлимо Вана Ваi перейдемо до границi при:

Аналогiчно знаходять похiдну, якщо число промiжних змiнних бiльше двох. Наприклад, якщо , де , то

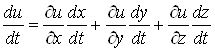.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11)

Зокрема, якщо, а, то

,

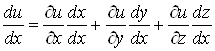а оскiльки , то

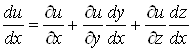.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (12)

Цю формулу називають формулою для обчислення повноi похiдноi
(на вiдмiну вiд частинноi похiдноi).

Розглянемо загальнiший випадок. Нехай ВатАУ функцiя двох змiнних Вата, якi, в свою чергу, залежать вiд змiнних :, , тодi функцiя Ваi складеною функцiiю незалежних змiнних Вата, а змiннi Вата ВатАУ промiжнi.

Аналогiчно попереднiй теоремi доводиться таке твердження.

Якщо функцii Вата Вадиференцiйовнi в точцi , а функцiя диференцiйовна в точцi , то складена функцiя Вадиференцiйовна в точцi Ваi ii частиннi похiднi знаходяться за формулами:

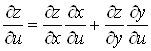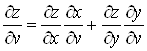; .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (13)

Формули (13) можна узагальнити на випадок бiльшого числа змiнних. Якщо, де, то

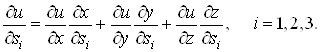
Знайдемо диференцiал складеноi функцii. Скориставшись формулами (13), отримаiмо

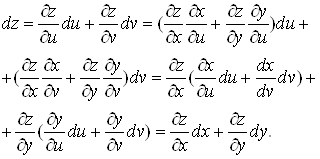
Отже, диференцiал функцii, де , , визначаiться формулою

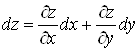,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (14)

де

.

Порiвнявши формули (14) i (4) дiйдемо висновку, що повний диференцiал функцii Вамаi iнварiантну (незмiнну) форму незалежно вiд того, чи i x та Ванезалежними змiнними, чи диференцiйовними функцiями змiнних u та v. Проте формули (4) i (14) однаковi лише за формою, а по сутi рiзнi, бо у формулi (4) iтАУ диференцiали незалежних змiнних, а у формулi (14) iтАУ повнi диференцiали функцiй Вата .

Диференцiали вищих порядкiв властивостi iнварiантностi не мають. Наприклад, якщо, де , , то

ВаВаВаВаВаВаВаВаВаВаВаВаВа (15)

Формула (15) вiдрiзняiться вiд формули (8), оскiльки для складеноi функцii диференцiали Вата Ваможуть i не дорiвнювати нулю. Отже, для складеноi функцii, де , , формула (8) неправильна.

5 Диференцiювання неявноi функцii

Нехай задано рiвняння

,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (16)

де ВатАУ функцiя двох змiнних.

Нагадаiмо, що коли кожному значенню x з деякоi множини Вавiдповiдаi iдине значення, яке разом з x задовольняi рiвняння (16), то кажуть, що це рiвняння задаi на множинi Ванеявну функцiю.

Таким чином, для неявноi функцii, заданоi рiвнянням (16), маi мiсце тотожнiсть

.

Якi ж умови маi задовольняти функцiя Ващоб рiвняння (16) визначало неявну функцiю i при тому iдину? Вiдповiдь на це запитання даi така теорема iснування неявноi функцii [8].

Теорема. Нехай функцiя Ваi ii похiднi Вата Вавизначенi та неперервнi у будь-якому околi точки Ваi , а; тодi iснуi окiл точки , в якому рiвняння Вавизначаi iдину неявну функцiю, неперервну та диференцiйовну в околi точки Ваi таку, що .

Знайдемо похiдну неявноi функцii. Нехай лiва частина рiвняння (16) задовольняi зазначенi в теоремi умови, тодi це рiвняння задаi неявну функцiю, для якоi на деякiй множинi точок x маi мiсце тотожнiсть. Оскiльки похiдна функцii, що тотожно дорiвнюi нулю, також дорiвнюi нулю, то повна похiдна. Але за формулою (12) маiмо 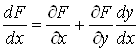, тому 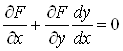, звiдки

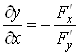.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (17)

За цiiю формулою знаходять похiдну неявноi функцii однiii змiнноi.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы

Анализ эмпирического распределения