Функцiя, ii границя та неперервнiсть

ФУНКЦРЖЯ, РЗРЗ ГРАНИЦЯ ТА НЕПЕРЕРВНРЖСТЬ

1. Функцiя багатьох змiнних. Означення та символiка

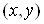Нехай задано множину Ваупорядкованих пар чисел. Якщо кожнiй парi чисел 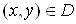за певним законом вiдповiдаi число z, то кажуть, що на множинi Вавизначено функцiю 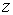Вавiд двох змiнних x i 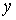Ваi записують.

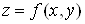Змiнну 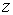Ваназивають залежною змiнною (функцiiю), а змiннi x та 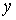ВатАУ незалежними змiнними (аргументами).

Множину пар 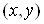Вазначень x та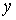, для яких функцiя 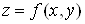Вавизначена, називають областю визначення цiii функцii i позначають 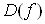Ваабо.

Множину значень 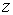Вапозначають 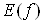або.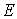

Оскiльки кожнiй упорядкованiй парi чисел 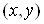Вавiдповiдаi в прямокутнiй системi координат 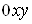Ваiдина точка 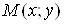Ваплощини, що те саме, точка двовимiрного простору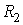, i, навпаки, кожнiй точцi 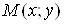Ваплощини вiдповiдаi iдина упорядкована пара чисел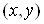, то функцiю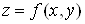, де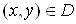, можна розглядати як функцiю точки 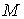Ваi замiсть 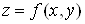Ваписати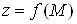. Областю визначення 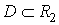Вафункцii у цьому випадку i деяка множина точок площини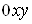. Зокрема, областю визначення функцii може бути вся площина, або частина площини, обмежена певними лiнiями.

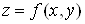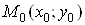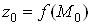Значення функцii Вав точцi Вапозначають Ваабо, або.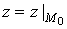

Лiнiю, що обмежуi область, називають межею областi визначення. Точки областi, якi не лежать на ii межi, називаються внутрiшнiми. Область, яка мiстить однi внутрiшнi точки називаiться вiдкритою. Якщо ж до областi визначення належать i всi точки межi, то така область називаiться замкненою.

Функцiя двох змiнних, як i функцiя однiii змiнноi, може бути задана рiзними способами. Користуватимемося, як правило, аналiтичним способом, коли функцiя задаiться за допомогою формули. Областю визначення такоi функцii вважаiться множина всiх тих точок площини, для яких задана формула маi змiст.

Приклади

Знайти область визначення функцii

а);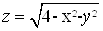

б).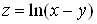

РозвтАЩязання

а) Область 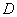Ваданоi функцii тАУ множина тих точок 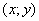, для яких вираз 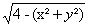маi змiст, тобто множина точок, для яких 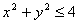. Це означаi, що функцiя визначена в точках, якi знаходяться всерединi кола 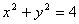Ваi на його межi, оскiльки всi точки, якi знаходяться зовнi кола задовольняють умову .

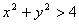б) Область визначення Вацiii функцii визначаiться з нерiвностi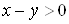, тобто.

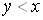Точки площини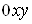, координати яких задовольняють цю нерiвнiсть, розташованi пiд прямою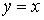, причому точки, якi розташованi на цiй прямiй не належать областi.

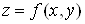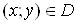Функцiю двох змiнних можна зобразити графiчно у виглядi деякоi поверхнi. Дiйсно, нехай функцiя Вавизначена в областi. Кожнiй точцi Вавiдповiдаi певне значення функцii.

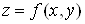Графiком функцii 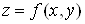Вау прямокутнiй системi 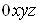Ваназиваiться геометричне мiсце точок 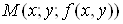, проекцii яких 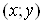Ваналежать областi. Це геометричне мiсце точок утворюi в тривимiрному просторi 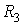Вапевну поверхню (рис.1), проекцiiю якоi на площину 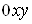Ваi множина.

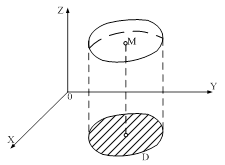
Рисунок 1 тАУ Поверхня у тривимiрному просторi

Приклади

а) Графiком функцii 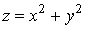, як вiдомо з аналiтичноi геометрii, i параболоiд обертання.

б) Графiком функцii 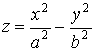i гiперболiчний параболоiд.

При побудовi графiкiв функцiй двох змiнних часто стикаiмося iз значними труднощами. В звтАЩязку з цим для зображення функцii двох змiнних користуються методом перерiзiв, який полягаi у тому, що поверхню 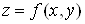перетинають площинами 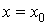Вата 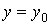Ваi за графiками кривих 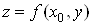та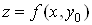визначають графiк функцii.

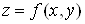Можна фiксувати неx чи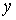, а саму функцiю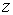, тобто перетинати дану поверхню площинами 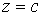, де c тАУ довiльне число, взяте з множини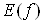значень даноi функцii. Таким чином отримаiмо криву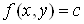, яку називають
лiнiiю рiвня функцii. РЖнакше кажучи, лiнiя рiвня на площинi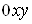ВатАУ це проекцiя кривоi, яка утворюiться при перетинi поверхнi 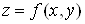Ваплощиною 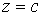. Якщо побудувати лiнii рiвня для рiзних значень c, можна отримати уявлення про графiк функцii двох змiнних.

Приклад

Знайти лiнii рiвня функцii .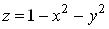

РозвтАЩязання

Лiнiями рiвня даноi функцii i кола з радiусом 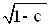Ва(рис. 2). Зокрема, якщо, то отримуiмо коло .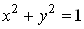

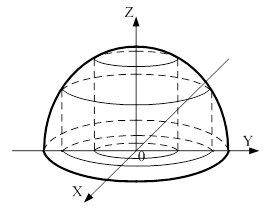
Рисунок 2 тАУ Лiнii рiвня функцii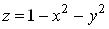

Поняття функцii двох змiнних узагальнимо на випадок трьох i бiльшого числа незалежних змiнних.

НехайтАУ деяка множина упорядкованих трiйок дiйсних чисел, тобто точок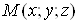тривимiрного простору.

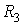Якщо кожнiй точцi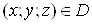Ваза певним законом вiдповiдаi iдине число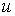, то кажуть, що на множинiВавизначено функцiюu вiд трьох змiнних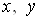Ваi 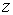та записують 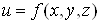Ваабо .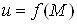

При цьому змiнна 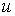Ваназиваiться залежною змiнною (функцiiю), тАУ незалежними змiнними (аргументами), множина 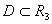ВатАУ областю визначення функцii.

Область визначення функцii трьох змiнних можна геометрично зобразити у виглядi деякоi частини тривимiрного простору.

Поверхнею рiвня функцii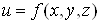Ваназивають множину всiх точок , для яких задана функцiя набуваi одне й те саме значення: .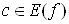

Приклади

Областю визначення функцii

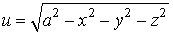
i куля радiуса 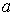з центром у початку координат. Це замкнена область, оскiльки iй належать точки сфери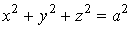ВатАУ межi областi.

2. Поверхнi рiвня функцii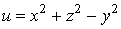визначаються рiвнянням,

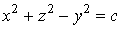В· Якщо , то отримуiмо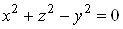тАУ конус;

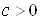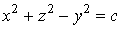В· якщо, тоВатАУ сiмтАЩя однопорожнинних гiперболоiдiв;

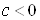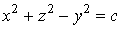В· якщо, то ВатАУ сiмтАЩя двопорожнинних гiперболоiдiв.

Лiнii та поверхнi рiвня досить часто зустрiчаються на практицi. Зокрема, iзотерми та iзобари i важливими даними для прогнозу погоди.

Якщо число n незалежних змiнних бiльше трьох, то iх часто позначають однiiю буквою, але з рiзними iндексами: .

Функцiю u вiд цих незалежних змiнних можна визначити так. Нехай задано множинуВаупорядкованих систем з n чисел 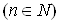Ваабо, що те саме, множину точок 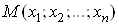ВаnтАУ вимiрного простору .

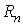Якщо кожнiй точцi 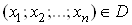за певним законом вiдповiдаi iдине число u, то кажуть, що на множинiВавизначено функцiю uвiд n змiнних: i записують

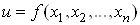або,.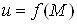

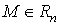Надалi розглядатимемо функцii двох змiнних, оскiльки результати для функцiй двох змiнних легко за аналогiiю узагальнити на випадок бiльшого числа змiнних.

2. Границя функцii багатьох змiнних

функцiя формула неперервнiсть змiнна

Введемо поняття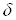ВатАУ околу заданоi точки 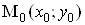i поняття збiжноi послiдовностi точок площини.

Множина всiх точок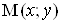, координати яких задовольняють нерiвнiсть

,

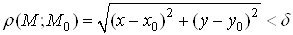де 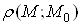ВатАУ вiдстань вiд точки 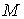Вадо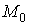, називаiться 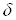-околом точки .

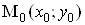Розглянемо послiдовнiсть точок, , 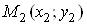тАж, 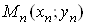, яку позначимо символом 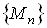. Послiдовнiсть точок 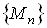називаiться збiжною до точки 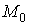, якщо для довiльного числа 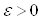Ваiснуi номер 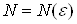такий, що при виконуiться нерiвнiсть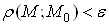. При цьому точку 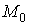Ваназивають границею послiдовностi 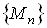Ваi записують так:

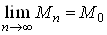або 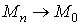Вапри.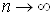

Якщо 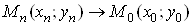при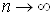, то, очевидно, 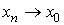, 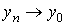Вапри.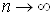

Тепер розглянемо границю функцii двох змiнних. РЗi означення аналогiчне означенню границi функцii однiii змiнноi. Нехай функцiя 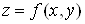Вазадана в деякiй областi Ваi точка 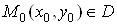або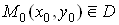, але маi таку властивiсть, що в довiльному 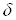-околi цiii точки мiститься хоча б одна точка множини, вiдмiнна вiд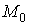_. Число 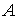Ваназиваiться границею функцii 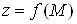в точцi 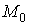, якщо для довiльноi, збiжноi до 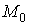Вапослiдовностi точок 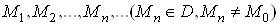, вiдповiдна послiдовнiсть значень функцii 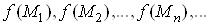збiгаiться до числа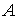. При цьому пишуть:

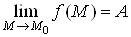, або.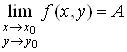

Наведене означення границi функцii називають означенням за Гейне або означенням тАЮна мовi послiдовностейтАЭ.

Дамо еквiвалентне означення границi функцii за Кошi або означення тАЮна мовi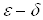тАЭ. Число 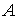Ваназиваiться границею функцii 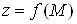в точцi 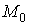, якщо для кожного числа 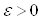Вазнайдеться число 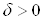Ватаке, що для всiх точок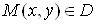, якi задовольняють умову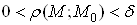, виконуiться нерiвнiсть.

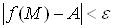Користуючись означенням границi функцii двох змiнних, можна перенести основнi теореми про границi для функцii однiii змiнноi на функцii двох змiнних. Наприклад, правильне таке твердження.

Теорема. Нехай функцi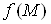i Ваi 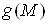Вавизначенi на однiй i тiй самiй
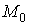множинi Ваi мають в точцi границ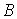i Ваi.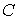

Тодi функцii, мають в
точцi 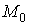границi,якi вiдповiдно дорiвнюють.

Функцiя 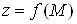Ваназиваiться нескiнченно малою в точцi 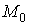Ва(або при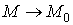), якщо .

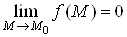Якщо функцiя 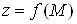Вамаi в точцi 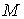Ваграницю, яка дорiвнюi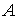, то
функцiя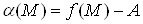Ваi нескiнченно малою в точцi 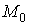_, тому що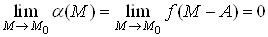. Звiдси випливаi, що функцiя 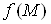в околi точки 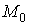вiдрiзняiться вiд границi 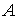Вана нескiнченно малу функцiю.

Приклади

Знайти границi:

а)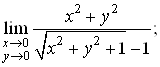

б)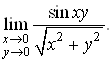

РозвтАЩязання

а) Якщ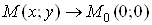о, то 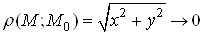, тому

.

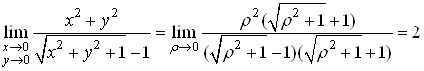б) Умова 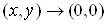Ваеквiвалентна умовi .

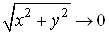Оскiльки ,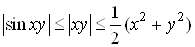

То

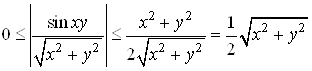
i, отже,

Означення границi функцii 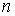Вазмiнних при 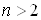Вааналогiчне означенням границi при 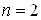Ва, якщо в 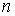-вимiрному просторi ввести таке поняття 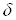-околу: 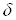-околом точки Ваназиваiться множина всiх точок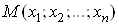, координати яких задовольняють нерiвностi

.

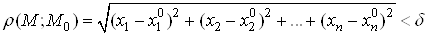Зокрема, у тривимiрному просторi 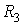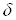-околом точки 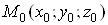Ваi множина всiх внутрiшнiх точок 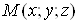Вакулi з центром у точцi 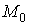Варадiуса.

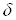3. Неперервнiсть функцii багатьох змiнних

Поняття неперервноi функцii багатьох змiнних вводиться за допомогою поняття границi.

Нехай функцiя 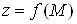Вавизначена на множинi, точка 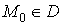Ваi довiльний 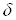-окiл точки 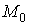Вамiстить точки множини.

Функцiя 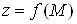Ваназиваiться неперервною в точцi 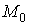, якщо

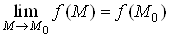.(1)

У випадку функцii двох змiнних рiвнiсть (1) означаi, що коли точка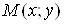, залишаючись в областi визначення функцii 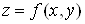, наближаiться до точки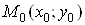, то вiдповiдна аплiката 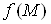поверхнi, яка i графiком заданоi функцii, прямуi до аплiкати.

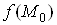Точки, в яких функцiя неперервна, називаються точками неперервностi, а точки, в яких неперервнiсть порушуiться тАУ точками розриву цiii функцii.

Приклад

Неперервнiсть функцii

в довiльнiй точцi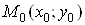, крiм точки, випливаi iз неперервностi многочлена, синуса, квадратного кореня i умови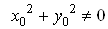; неперервнiсть 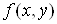Вав точцi 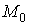(0;0) випливаi iз рiвностi

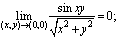(п. 2).

Умовi (1) неперервностi можна надати iншого вигляду. Позначимо

, ,.

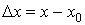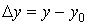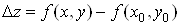Величини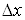, 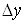Ваназивають приростами аргументiв x i 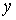, а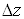тАУ повним приростом функцii 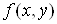Вав точцi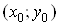. З рiвностi (1) отримуiмо:

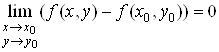
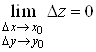.(2)

Рiвнiсть (2) даi ще одне означення неперервностi.

Функцiя 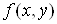Ваназиваiться неперервною в точцi 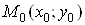, якщо повний прирiст ii в цiй точцi прямуi до нуля, коли прирости ii аргументiв x та 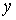прямують до нуля.

Функцiя 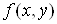Ваназиваiться неперервною на множинi , якщо вона неперервна в кожнiй точцi 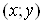Вацiii множини.

Приклад

Функцiя 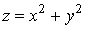Ванеперервна на всiй площинi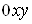, оскiльки повний прирiст цiii функцii в довiльнiй точцi 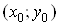Вамаi вигляд

.

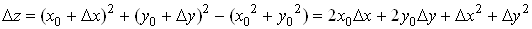
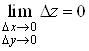Використовуючи поняття неперервностi функцii кiлькох змiнних i вiдповiднi теореми про границi, можна довести, що арифметичнi операцii над неперервними функцiями i побудова складеноi функцii з неперервних функцiй приводять до неперервних функцiй.

Наведемо основнi властивостi функцii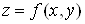, неперервноi в замкненiй i обмеженiй областi. Цi властивостi аналогiчнi властивостям неперервноi на вiдрiзку функцii однiii змiнноi. Попередньо уточнимо ряд понять для множин точок площини.

Множина Ваточок площини називаiться звтАЩязною, якщо будь-якi ii двi точки можна зтАЩiднати неперервною лiнiiю, яка повнiстю належить множинi.

Точка 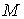називаiться внутрiшньою точкою множини, якщо iснуi
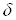-окiл цiii точки, який повнiстю мiститься у множинi.

Множину називають вiдкритою, якщо кожна ii точка внутрiшня.

Областю (або вiдкритою областю) називають звтАЩязну вiдкриту множину точок.

Точку 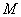Ваназивають межовою точкою множини 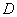, якщо будь-який ii окiл мiстить як точки, що належать 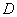, так i точки, що не належать множинi 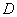. Множину всiх межових точок областi називають межею областi.

Область разом з ii межею називаiться замкненою. Якщо iснуi круг скiнченного радiуса, який повнiстю мiстить область, то вона називаiться обмеженою.

Замкнена область, в якiй визначена функцiя двох змiнних, i аналогом вiдрiзка для функцii однiii змiнноi.

Тепер сформулюiмо властивостi неперервних функцiй двох змiнних у замкненiй обмеженiй областi.

1. Якщо функцiя 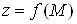неперервна в замкненiй обмеженiй областi, то вона обмежена в цiй областi, тобто iснуi таке число 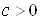, що для всiх точок областi виконуiться нерiвнiсть.

2. Якщо функцiя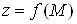неперервна в замкненiй обмеженiй областi, то в цiй областi iснують точки, в яких функцiя набуваi найбiльшого i найменшого значень.

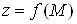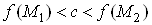3. Якщо функцiянеперервна в замкненiй обмеженiй областi Ваi, де 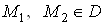, то iснуi точка 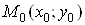Вав якiй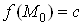. Зокрема, якщо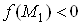, а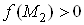, то в областi Ваiснуi точка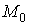, в якiй.

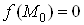Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

Автокорреляционная функция. Примеры расчётов

Актуальные проблемы квантовой механики

Алгебра и алгебраические системы

Анализ эмпирического распределения