Алгебраические системы замыканий
Содержание
Введение. 3
Вз1. Основные понятия и примеры. 6
Вз2. Связь систем замыканий с операторами замыкания. 13
Вз3. Алгебраические системы замыканий. 16
Вз4. Соответствия Галуа. 20
Вз 5. Задачи. 27
Библиографический список. 32
ВведениеВажную роль в математике играет множество подалгебр данной алгебры относительно отношения включения 
. Оно образует полную решётку с некоторыми характерными свойствами. Понятие замыкания также играет важную роль в алгебре и топологии. В данной дипломной работе рассматриваются основные свойства систем замыканий на множествах, взаимосвязь систем замыканий с операторами замыкания и соответствиями Галуа. Соответствия Галуа представляют собой достаточно интересный класс объектов. Они возникли и получили своё название из теории Галуа, но спустя некоторое время стали применяться не только в самой теории, но и во многих других областях математики. В данной работе соответствия Галуа будем рассматривать в качестве одного из наиболее важных примеров систем замыканий.
Целью квалификационной работы является изучение абстрактных систем замыканий на множестве.
Задачи:
1. рассмотреть понятие системы замыкания, проиллюстрировать это понятие на примерах;
2. сформулировать и доказать теорему о взаимосвязи между системами замыканий и операторами замыкания;
3. рассмотреть понятие алгебраических систем замыканий, сформулировать и доказать теорему об описании структуры алгебраических систем замыканий;
4. рассмотреть понятие соответствия Галуа, примеры соответствий Галуа. Установить связь соответствий Галуа с системами замыканий.
Исходя из цели и задач, дипломная работа состоит из пяти параграфов. В качестве первого шага введём необходимые определения и докажем ряд простых предложений. Этому отводится параграф 1.
В параграфе 2 докажем основную теорему об операторе замыканий, которая даёт прямой выход на соответствия Галуа.
В параграфе 3 сформулируем и докажем одну из наиболее важных теорем о структуре алгебраических систем замыканий.
Параграф 4 будет полностью посвящен соответствиям Галуа: определение, основные примеры и их связь с системами замыканий.
Последний параграф посвящен решению задач.
Основной литературой при написании квалификационной работы стали монографии Кона П. ([1]) и Куроша А. Г. ([2], [3]). Остальные источники ([4], [5], [6], [7]) использовались как дополнительная справочная литература.
Для удобства в данной работе использованы следующие обозначения:
∆ тАУ начало доказательства;
▲ тАУ конец доказательства.
В работе принята сквозная двойная нумерация примеров, где первое число тАУ номер параграфа, а второе тАУ номер примера в параграфе.
Основными результатами работы являются:
1. доказательство теоремы о взаимосвязи между системами замыканий и операторами замыкания: Каждаясистемазамыканий D намножествеAопределяетоператор замыкания на A по правилу (X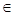) = ∩{Y 
D | Y
X}.Обратно, каждый оператор замыкания на A определяет систему замыканий D = {XA (X) = X}.
2. доказательство теоремы о структуре алгебраических систем замыканий: СистемаS(A) подалгебруниверсальнойалгебрыAявляетсяалгебраическойсистемойзамыканий. Обратно, еслиданаалгебраическаясистемазамыканий D намножествеA, тодляподходящегомножестваалгебраическихопераций Ω можноопределитьтакуюструктурууниверсальнойалгебрынаA, чтоS(A) = D.
3. установление связи соответствий Галуа с системами замыканий на конкретных примерах.
4. решение задач.
Вместе с этим смотрят:
10 способов решения квадратных уравнений
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнженерна графiка
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй