Восьмиэлементные ассоциативные кольца
Понятие кольца появилось в математике в конце XIX века. Первыми примерами ассоциативных колец были числовые кольца, т.е. подкольца поля комплексных чисел и кольца классов вычетов целых чисел. Как самостоятельная область алгебры, теория ассоциативных колец оформилась к началу XX века. Из этой теории выделились в самостоятельные области алгебры теории коммутативных колец, тел, алгебр.
Дадим основные понятия, которыми мы будем пользоваться в дальнейшем.
Аддитивной абелевой группой 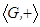 называется алгебра с бинарной операцией + (сложение), удовлетворяющей следующим аксиомам:
называется алгебра с бинарной операцией + (сложение), удовлетворяющей следующим аксиомам:
1) сложение ассоциативно, т.е.  ;
;
2) в G существует нейтральный элемент 0 (ноль) такой, что 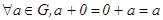 ;
;
3) в G для любого элемента существует противоположный элемент, т.е.  ;
;
4) Сложение коммутативно: 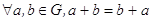 ;
;
Мультипликативной полугруппой  называется алгебра с бинарной операцией
называется алгебра с бинарной операцией 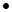 (умножение), удовлетворяющая закону ассоциативности:
(умножение), удовлетворяющая закону ассоциативности: 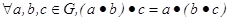 ; (в дальнейшем мы будем писать ab, и иметь ввиду произведение элементов aи в G.
; (в дальнейшем мы будем писать ab, и иметь ввиду произведение элементов aи в G.
Кольцом называется алгебра 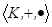 с двумя бинарными операциями сложения и умножения, которые удовлетворяют следующим условиям:
с двумя бинарными операциями сложения и умножения, которые удовлетворяют следующим условиям:
1) относительно сложения кольцо является абелевой группой;
2) относительно умножения тАУ это полугруппа;
3) выполняются законы дистрибутивности: 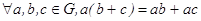 и
и 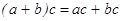 ;
;
Данная дипломная работа представляет собой изложение методики изучения определенных конечных алгебр. В настоящее время изучение конечных алгебр производится с помощью компьютера. Задача данной дипломной работы состоит в отыскании всех восьмиэлементных ассоциативных колец. Для этого мы сначала находим все абелевы группы из восьми элементов, а затем для каждой такой группы строим соответствующие полугруппы по умножению, и получаем искомые кольца.
Всего абелевых групп по сложению, с точностью до изоморфизма, будет три:  ,
,  , и
, и 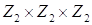 . Для группы
. Для группы  , кольца находятся вручную. Для нахождения колец по остальным двум группам нужно использовать компьютер, так как количество всевозможных полугрупп по умножению будет велико и, соответственно, отбор восьмиэлементных колец без привлечения вычислительной машины займет очень много времени.
, кольца находятся вручную. Для нахождения колец по остальным двум группам нужно использовать компьютер, так как количество всевозможных полугрупп по умножению будет велико и, соответственно, отбор восьмиэлементных колец без привлечения вычислительной машины займет очень много времени.
В результате получаем, что всего существует с точностью до изоморфизма 392 восьмиэлиментных кольца.
Для работы с абелевыми группами и полугруппами по умножению, а также для представления их в компьютере, будем пользоваться таблицами Кэли. Таблицей Кэли называется квадратная таблица произвольной алгебры, задаваемая для определённой бинарной операции. Заглавная строка таблицы заполняется в некотором порядке символами, обозначающими различные элементы, теми же символами и в том же порядке заполняется главный столбец. Если алгебра обладает нейтральным элементом, то этот элемент, как правило, помещается на первом месте. Если на i-м месте в заглавном столбце стоит символ ai, и на j-м месте в заглавной строке тАУ символ aj, то на пересечении i-ой строки и j-го столбца записывается символ, обозначающий результат операции элементов ai и aj. В нашем случае мы не будем писать заглавные строки таблицы, подразумевая, что элементы пронумерованы числами от 0 до 7. Мы будем использовать таблицы Кэли без заглавных строки и столбца.
Вз1. Абелевы группы по сложению
Как уже было сказано выше, всего восьмиэлементных аддитивных абелевых групп с точностью до изоморфизма три:  ,
,  , и
, и 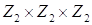 .
.
Представим каждую из таких групп в виде таблиц Кэли. Для группы  элементы представим числами от 0 до 7. Элементы для групп
элементы представим числами от 0 до 7. Элементы для групп  и
и 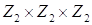 обозначим следующим образом:
обозначим следующим образом:

| 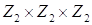
|
0º (0,0) 1º (1,0) 2º (2,0) 3º (3,0) 4º (0,1) 5º (1,1) 6º (2,1) 7º (3,1) | 0º (0,0,0) 1º (1,0,0) 2º (0,1,0) 3º (0,0,1) 4º (1,1,0) 5º (1,0,1) 6º (0,1,1) 7º (1,1,1) |
Таким образом, группы будут иметь следующий вид:

| 
| 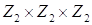
|
0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 0 2 3 4 5 6 7 0 1 3 4 5 6 7 0 1 2 4 5 6 7 0 1 2 3 5 6 7 0 1 2 3 4 6 7 0 1 2 3 4 5 7 0 1 2 3 4 5 6 | 0 1 2 3 4 5 6 7 1 2 3 0 5 6 7 4 2 3 0 1 6 7 4 5 3 0 1 2 7 4 5 6 4 5 6 7 0 1 2 3 5 6 7 4 1 2 3 0 6 7 4 5 2 3 0 1 7 4 5 6 3 0 1 2 | 0 1 2 3 4 5 6 7 1 0 4 5 2 3 7 6 2 4 0 6 1 7 3 5 3 5 6 0 7 1 2 4 4 2 1 7 0 6 5 3 5 3 7 1 6 0 4 2 6 7 3 2 5 4 0 1 7 6 5 4 3 2 1 0 |
Затем, для каждой такой группы, мы будем строить полугруппы по умножению, пользуясь также таблицами Кэли. Для группы  таких полугрупп будет всего 8, так как нам достаточно определить чему равно произведение 1В·1. На место этого произведения мы можем поставить один из 8 элементов (от 0 до 7), а все остальные элементы будут определяться однозначно, согласно дистрибутивному закону. Ассоциативность умножения будет выполнятся, так как умножение сводится к сложению. Кроме того, умножение будет коммутативно. Таким образом, после вычеркивания изоморфных, мы получим 4 кольца с абелевой группой по сложению
таких полугрупп будет всего 8, так как нам достаточно определить чему равно произведение 1В·1. На место этого произведения мы можем поставить один из 8 элементов (от 0 до 7), а все остальные элементы будут определяться однозначно, согласно дистрибутивному закону. Ассоциативность умножения будет выполнятся, так как умножение сводится к сложению. Кроме того, умножение будет коммутативно. Таким образом, после вычеркивания изоморфных, мы получим 4 кольца с абелевой группой по сложению  :
:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 1 2 3 4 5 6 7 0 2 4 6 0 2 4 6 0 3 6 1 4 7 2 5 0 4 0 4 0 4 0 4 0 5 2 7 4 1 6 3 0 6 4 2 0 6 4 2 0 7 6 5 4 3 2 1 | 0 0 0 0 0 0 0 0 0 2 4 6 0 2 4 6 0 4 0 4 0 4 0 4 0 6 4 2 0 6 4 2 0 0 0 0 0 0 0 0 0 2 4 6 0 2 4 6 0 4 0 4 0 4 0 4 0 6 4 2 0 6 4 2 | 0 0 0 0 0 0 0 0 0 4 0 4 0 4 0 4 0 0 0 0 0 0 0 0 0 4 0 4 0 4 0 4 0 0 0 0 0 0 0 0 0 4 0 4 0 4 0 4 0 0 0 0 0 0 0 0 0 4 0 4 0 4 0 4 |
В случае с группой  в полугруппе по умножению уже будет 4 независимых произведения, т.е. это такие элементы в таблице Кэли для полугруппы по умножению, на которые мы можем поставить любой из элементов от 0 до 7. Соответственно всего различных колец без учета ассоциативности и вычеркивания изоморфных будет 84. Проверка ассоциативности умножения и выделение изоморфных колец осуществляется программным способом. Чтобы найти кольцо, изоморфное данному, нужно сначала найти все автоморфизмы абелевой группы по сложению, а потом этими преобразованиями подействовать на полугруппы по умножению, и соответственно получившиеся одинаковые кольца вычеркнуть. Автоморфизмы группы
в полугруппе по умножению уже будет 4 независимых произведения, т.е. это такие элементы в таблице Кэли для полугруппы по умножению, на которые мы можем поставить любой из элементов от 0 до 7. Соответственно всего различных колец без учета ассоциативности и вычеркивания изоморфных будет 84. Проверка ассоциативности умножения и выделение изоморфных колец осуществляется программным способом. Чтобы найти кольцо, изоморфное данному, нужно сначала найти все автоморфизмы абелевой группы по сложению, а потом этими преобразованиями подействовать на полугруппы по умножению, и соответственно получившиеся одинаковые кольца вычеркнуть. Автоморфизмы группы  будем искать вручную. Выделим в данной группе элементы 1, 3, 5, 7 тАУ элементы четвертого порядка. Остальные элементы будут выражаться через них: 4=1+7, 6=1+5, 2=4+6 тАУ это элементы второго порядка. Пары элементов 1º(1,0), 3º(3,0) и 5º(1,1), 7º(3,1) тАУ противоположные друг другу элементы. Нам достаточно посмотреть, как будут вести себя элементы четвертого порядка при автоморфизмах. Это будут 6 взаимнооднозначных отображений, в том числе и тождественное, которые переводят данную группу в себя:
будем искать вручную. Выделим в данной группе элементы 1, 3, 5, 7 тАУ элементы четвертого порядка. Остальные элементы будут выражаться через них: 4=1+7, 6=1+5, 2=4+6 тАУ это элементы второго порядка. Пары элементов 1º(1,0), 3º(3,0) и 5º(1,1), 7º(3,1) тАУ противоположные друг другу элементы. Нам достаточно посмотреть, как будут вести себя элементы четвертого порядка при автоморфизмах. Это будут 6 взаимнооднозначных отображений, в том числе и тождественное, которые переводят данную группу в себя:
1Во3 3Во1 5Во7 7Во5 4Во4 6Во6 2Во2 | 1Во1 3Во3 5Во7 7Во5 4Во6 6Во4 2Во2 | 1Во3 3Во1 5Во5 7Во7 4Во6 6Во4 2Во2 | 1Во5 5Во1 3Во7 7Во3 4Во4 6Во6 2Во2 | 1Во7 7Во1 3Во5 5Во3 4Во4 6Во6 2Во2 |
Вместе с этим смотрят:
10 способов решения квадратных уравнений
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнженерна графiка
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй