Дискретная математика
Министерство образования и науки
Российской Федерации
Российский химико-технологический университет
им. Д.И. Менделеева
Новомосковский институт
Издательский центр
T.П. Тюрина, В.И. Емельянов
Дискретная математика
(часть 3)
Учебное пособие
Новомосковск 2004
Содержание
Часть 3. Элементы алгебры логики.............................. 3
3.1 Введение в алгебру логики.................................... 3
3.2 Основные функции алгебры логики............................. 5
3.3 Формулы алгебры логики.................................... 9
Контрольные вопросы......................................... 12
3.4 Законы алгебры логики и следствия из них...................... 12
Контрольные вопросы......................................... 16
3.5 Логические функции многих переменных....................... 16
3.6 Построение формул алгебры логики по заданной таблице истинности 18
Контрольные вопросы и упражнения............................. 26
3.7 Некоторые замкнутые классы (классы Поста). Понятие базиса...... 26
Контрольные вопросы и упражнения............................. 34
3.8 Методы минимизации логических функций...................... 34
Контрольные вопросы......................................... 39
3.9 Неполностью определенные логические функции................. 40
3.10 Формы представления булевых функций...................... 41
3.10.1 Семантические деревья................................... 42
3.10.2 Бинарные диаграммы решений (БДР)........................ 45
3.11 Построение логических схем................................ 45
Контрольные вопросы......................................... 45
3.12 Логические конечные автоматы.............................. 46
3.12.1 Процессы.............................................. 50
3.12.2 Конечные автоматы...................................... 52
Контрольные вопросы......................................... 55
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.............................. 60
Часть 3. Элементы алгебры логики
3.1 Введение в алгебру логики
Алгебру логики иначе еще называют алгеброй высказываний, логикой высказываний. Алгебра логики начала формироваться в 19 веке в трудах английского математика Дж. Буля.
Прежде всего, благодаря труду английского логика Джорджа Буля ВлМатематический анализ логикиВ», был достигнут подлинный прогресс науки, называемый математической логикой. Он перенёс на логику законы и правила математических действий, ввёл логические операции, предложил способ записи высказываний в символической форме.
В трудах Джорджа Буля и О. де Моргана математическая логика представлена как своеобразная алгебра тАУ алгебра логики (алгебра высказываний).
Алгебра логики (алгебра высказываний) тАУ раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Джордж Буль (1815тАУ1864) родился в Линкольне (Англия). Сын сапожного мастера. Окончил только начальную школу и дальнейшие знания приобретал самоучкой. С 1849 г. Буль тАУ профессор математики в Куинс тАУ колледже в Корке (Ирландия), где преподавал до конца жизни. Буля почти в равной степени интересовали логика, математический анализ, теория вероятностей, этика Б. Спинозы, философские работы Аристотеля и Цицерона. Он считается несомненным создателем современной символической (математической) логики.
Огастес де Морган (1806тАУ1871) родился в Индии в семье полковника английских войск. Получил образование в Кембриджском университете. Был профессором математики Лондонского университета. Математику и логику де Морган назвал азами точного знания и выражал сожаление, что математики не более заботятся о логике, чем логики о математике. Сам он стремился сблизить обе науки, и его главной заслугой явилось построение логики по образу и подобию математических наук. Независимо от Дж. Буля он открыл основные идеи алгебры логики.
ВлЛогика БуляВ» основывается на отношении эквивалентности, при котором правая часть равенства всегда содержит ровно столько же ВлистинВ», сколько и левая.
Высказывание тАУ это имеющее смысл языковое выражение (повествовательное предложение), относительно которого в данной ситуации можно утверждать, что оно либо истинно, либо ложно, т. е. каждому высказыванию можно приписать истинное значение И (истина) или Л (ложь), но не то и другое одновременно.
Примеры:
1. НГТУ тАУ крупнейший Влвуз НовосибирскаВ».
2. ВлСнег зелёныйВ».
3. Р= ВлЧтобы подключиться к Интернету с домашнего компьютера, необходим модем и соответствующее ПОВ».
4. Крокодилы летают очень низко.
ВлА ты любишь информатику?В» тАУ это предложение не является высказыванием.
Уравнение 2+х=4 не является высказыванием. Однако, всякий раз, придавая переменной х определенное числовое значение, будем получать высказывание. Используя частицу ВлнеВ», а также союзы ВлиВ», ВлилиВ», связки Влесли тАж., тотАжВ», Влтогда и только тогда, когдатАжВ» и т. п., можно из одних высказываний строить другие высказывания.
Изучением высказываний занимается Булева алгебра, в которой предполагается, что уже имеется некоторый запас высказываний, для каждого из которых известно истинно оно или ложно. Такие высказывания называют элементарными высказываниями. Из элементарных высказываний могут быть построены сложные с помощью операций алгебры логики.
Знаки логических операций называют логическими связками (или просто связками). Логические связки могут быть одноместные (унарные), двухместные (бинарные), трехместные (тернарные) и т. д.
В алгебре логики логические операции чаще всего описываются при помощи таблиц истинности, содержащих все наборы значений переменных и значения функции этих наборов. Алгебра логики не занимается обоснованием того, почему тому или иному элементарному высказыванию приписано значение истины или лжи. Этот вопрос решается за пределами алгебры логики.
Например: сумма углов в треугольнике тАУ 180 градусов. Алгебра логики отвлекается и от смысловой содержательности высказывания. Она интересуется только одним свойством сложных высказываний: быть истинным (True тАУ 1) или ложным (False тАУ 0).
Основной задачей теории булевых функций является разработка систематического метода построения сложных функций из более простых. Этот метод основан на изучении свойств булевых функций.
Основными символами алгебры высказываний являются:
а) пропозиционные переменные Р1, Р2, Р3, тАж;
б) одноместная связка тАУ (ù) и двуместные связки Ù (и), Ú (или), Во, Þ, Û;
в) скобки ().
Переменная, значениями которой являются высказывания, называется пропозиционной переменной.
Пусть А, В-некоторые элементарные высказывания.
Определим новое высказывание Ā (т. е. не А), будем называть его отрицанием (инверсия:  , Ā), представим таблицы значений функции отрицания:
, Ā), представим таблицы значений функции отрицания:
Рассмотрим наборы истинных значений элементарных функций на наборах аргументов:
Таблица 1
| № | Обозначение операции | Другие обозначения | Набор истинных значений | Название логической опции и связки | Как читается | Арифметическая модель |
| 12 | АÚВ | А+В Max (А, В) | 0 1 1 1 | Дизъюнкция, логическое сложение, ВлилиВ» | А или В | A+B-A×B |
| 23 | АÙВ | А&В А×В Min (А, В) | 0 0 0 1 | Конъюнкция, логическое умножение ВлиВ» | А и В | A×B |
| 34 | АВоВ | АÊВ АÞВ | 1 1 0 1 | Импликация, логическое следование | Если А, то В А влечет В | 1‑A+ A×B |
| 45 | А~В | АºВ АВлВ АÛВ | 1 0 0 1 | Эквиваленция, эквивалентность | А тогда и только тогда, когда В; А эквивалентно В | 1 тАУ (A-B)2 |
| 56 | АÅВ | А+В АÚВ АDВ | 0 1 1 0 | Сумма по модулю 2, сумма Жегалкина | А плюс В; Либо А, либо В | |
| 67 | А½В | | 1 1 1 0 | Штрих Шеффера, антиконъюнкция | Неверно, что А и В; А штрих Шеффера В | |
| 78 | А¯В | А° АÚВ | 1 0 0 0 | Стрелка Пирса, антидизъюнкция, функция Вебба, функция Даггера | Ни А, ни В; А стрелка Пирса В | |
Несмотря на то, что булевых функций от любого заданного числа m двоичных переменных конечное число, их слишком много, чтобы иметь запас преобразователей для любых встретившихся отображений. Рассмотрим сначала все возможные функции от одной двоичной переменной. Их четыре, две из них тАУ константы (0 и 1), одна тАУ тождественная функция и только одна тАУ функция отрицания (функция НЕ) тАУ является нетривиальной.
| p |  p p
|
| 0 | 1 |
| 1 | 0 |
Очевидно, что число различных булевых функций от mпеременных равно 2 в степени  . При m = 2 это число 16, то есть всего функций от двух переменных 16, однако наиболее практически применимых из них меньше.
. При m = 2 это число 16, то есть всего функций от двух переменных 16, однако наиболее практически применимых из них меньше.
Суперпозиция двоичных функций может быть записана как формула, которую называют логической формулой.
Пример.
Логическая формула 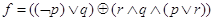 задает функцию от трех переменных как суперпозицию функций одной и двух переменных.
задает функцию от трех переменных как суперпозицию функций одной и двух переменных.
Для уменьшения числа скобок вводятся приоритеты операций. Наиболее приоритетна функция отрицания. Затем идет конъюнкция, после нее тАУ дизъюнкция. Все другие функции имеют равный приоритет, меньший, чем у дизъюнкции. Очевидно, что скобками можно установить желаемый порядок операций. Вышеприведенная формула может быть эквивалентно записана так: 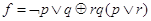 . Отметим, что используют и другое распределение приоритетов, в частности, полагая импликацию менее приоритетной, чем все другие функции.
. Отметим, что используют и другое распределение приоритетов, в частности, полагая импликацию менее приоритетной, чем все другие функции.
Логическая формула дает возможность построить соответствующий функциональный преобразователь, если мы имеем ВлэлементарныеВ» или ВлбазисныеВ» преобразователи. Для реализации преобразователя f примера выше необходимо иметь элементы, реализующие отрицание, дизъюнкцию, конъюнкцию и сложение по модулю два (см. рис. 1).
На этом рисунке представлен пример синтаксической структуры формулы тАУ графическое представление формулы.
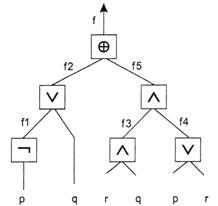
Рис. 1. Синтаксическая структура формулы 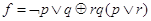
Очевидным образом по формуле можно построить табличное представление функции f.
Таблица 2
| p | q | r | 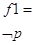
| 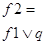
| 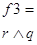
| 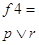
| 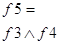
| 
|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
Суперпозицией нескольких простых булевых функций можно построить более сложную функцию, в частности, булеву функцию от большего числа переменных. Поставим вопрос: можно ли суперпозицией фиксированного набора функций представить любую булеву функцию от любого числа переменных? Удивительно, но ответ на этот вопрос положителен.
Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса тАУ отрицание дизъюнкции, сумма Жегалкина тАУ отрицание эквивалентности.
М. Жегалкин (1869тАУ1947) тАУ российский математик и логик, один из основоположников современной математической логики.
Чарльз Пирс (1839тАУ1914) тАУ американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник прагматизма.
Из логических переменных можно составлять различные конструкции, которые образуют формулы алгебры логики.
Пусть 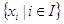 тАУ некоторое множество логических переменных. По индукции определим понятие формулы алгебры логики:
тАУ некоторое множество логических переменных. По индукции определим понятие формулы алгебры логики:
1) любая логическая переменная является формулой (атомарной);
2) если 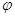 и
и  тАУ формулы, то выражения
тАУ формулы, то выражения 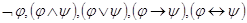 и другие, представленные в табл. 1, являются формулами;
и другие, представленные в табл. 1, являются формулами;
3) никаких других формул, кроме построенных в пунктах 1 и 2, нет.
Если формула 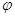 построена из логических переменных, лежащих в множестве {x1, x2,тАж, xn}, то будем писать
построена из логических переменных, лежащих в множестве {x1, x2,тАж, xn}, то будем писать 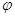 {x1, x2,тАж, xn}.
{x1, x2,тАж, xn}.
Таблицы истинности также называются интерпретациями логических операций и составляют семантику формул (т. е. придание смысла формулам) в отличие от синтаксиса формул (т. е. формальных законов их построения, данных в определении формулы).
На множестве  вводится транзитивное отношение < Влбыть более сильнымВ» и отношение ~ Влбыть равносильнымВ» по правилам, представленным на рис. 2. Для равносильных связок расстановка скобок выполняется слева направо.
вводится транзитивное отношение < Влбыть более сильнымВ» и отношение ~ Влбыть равносильнымВ» по правилам, представленным на рис. 2. Для равносильных связок расстановка скобок выполняется слева направо.
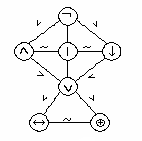
Рис. 2. Приоритетность логических операций
Все формулы алгебры логики можно разделить на 3 класса:
1) нейтральные, или выполнимые тАУ принимающие как истинное, так и ложное значения;
2) тождественно истинные формулы (или тавтологии) тАУ принимающие истинные значения при любых значениях переменных;
3) тождественно ложные формулы тАУ принимающие ложные значения при любых оценках переменных.
Существует два способа определения истинного значения формулы. Первый тАУ с помощью таблиц истинности, а второй тАУ путём приведения формул к нормальной форме. Формула имеет нормальную форму, если в ней отсутствуют знаки эквиваленции, импликации, двойного отрицания и др., при этом знаки отрицания находятся только при переменных.
Табличный способ определения истинного значения формул имеет ограниченное применение, поскольку при увеличении количества переменных приходится рассматривать слишком много вариантов (2N).
Равносильными называются два высказывания, у которых таблицы истинности совпадают.
Пример. Составим таблицу истинности функции f=(A B)~(
B)~(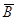
 ):
):
Таблица 3
| A | B | A B B | 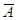
| 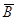
| 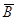 
| (A B)~( B)~(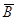  ) ) |
0 0 1 1 | 0 1 0 1 | 1 1 0 1 | 1 1 0 0 | 1 0 1 0 | 1 1 0 1 | 1 1 1 1 |
Полученное высказывание истинно всегда. Такие высказывания называют тождественно истинными и обозначаются J. По аналогии существуют и тождественно ложные высказывания L. Метод заполнения таблицы истинности принят для не очень сложных высказываний. Если выражение содержит N опций, то таблица становится громоздкой. Для этого используются законы алгебры логики. Таблицу истинности можно составить с использованием программы. В большинстве языков высокого уровня имеются логические операции NOT, AND, OR, XOR, реализующие операции 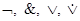 соответственно.
соответственно.
1. Дайте определение высказывания.
2. Перечислите основные символы алгебры высказываний.
3. Перечислите основные функции алгебры логики.
4. Что является основной задачей алгебры логики?
5. Что такое таблицы истинности логических функций?
6. Составьте таблицу истинности функций дизъюнкции и конъюнкции.
7. Составьте таблицу истинности функций импликации и эквивалентности.
8. Составьте таблицу истинности функций отрицания и сложения по модулю 2.
9. Составьте таблицу истинности функций Штрих Шеффера и Стрелка Пирса.
10. Формулы алгебры логики. Приоритет логических операций. Какие отношения имеют место на множестве логических операций?
11. Что такое синтаксическая структура формулы?
12. На какие классы делятся формулы алгебры логики?
При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре логики производится на основе эквивалентных преобразований, опирающихся на основные логические законы. Законы алгебры логики тАУ это тавтологии (или теоремы).
1. Закон тождества:
А=А
2. Закон непротиворечия:
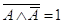

3. Закон исключения третьего:
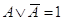
4. Закон двойного отрицания:
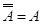
5. Законы истины и лжи (свойства констант):
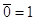
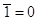
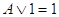
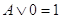
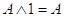
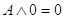
6. Законы идемпотентности:

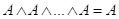
7. Коммутативные законы:
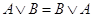
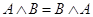
8. Ассоциативные законы:
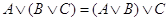 тАУ дизъюнкции
тАУ дизъюнкции
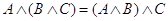 тАУ конъюнкции
тАУ конъюнкции
9. Дистрибутивные законы:
 тАУ 1‑ый дистрибутивный закон
тАУ 1‑ый дистрибутивный закон
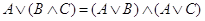 тАУ 2‑ой дистрибутивный закон
тАУ 2‑ой дистрибутивный закон
10. Законы поглощения:
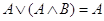

11. Законы де Моргана:
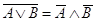
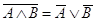
12. Закон импликации:
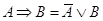
13. Закон эквивалентности:
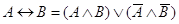
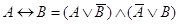
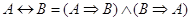
14. Свойства сложения Влпо модулю дваВ»:

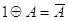
Справедливость этих законов можно доказать с помощью таблиц истинности сложных логических связей описываемых законов.
Следствия из законов алгебры логики (часто используются при упрощении логических выражений).
1. Правило поглощения. Данное правило является следствием из дистрибутивного закона. Оно может быть записано в следующем виде:
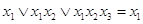 .
.
2. Правило свертки. Правило является следствием из второго дистрибутивного закона. Запись правила:
а) 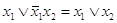 ;
;
б)  .
.
3. Правило расширения. Правило записывается в следующем виде:
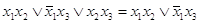 .
.
4. Правило склеивания. Базируется на понятии соседних конъюнкций. Соседними называются конъюнкции, отличающиеся представлением одной переменной. Например, конъюнкции 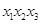 и
и 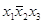 ,
, 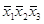 и
и 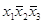 являются попарно соседними. В первой паре конъюнкции отличаются представлением х2, а во второй тАУ представлением х1. По этим переменным конъюнкции склеиваются.
являются попарно соседними. В первой паре конъюнкции отличаются представлением х2, а во второй тАУ представлением х1. По этим переменным конъюнкции склеиваются.
Формулировка правила: две соседние конъюнкции склеиваются с образованием одной конъюнкции меньшего ранга; исчезает та переменная, по которой конъюнкция склеивается.
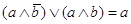 ,
, 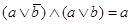 .
.
1. Перечислите основные законы алгебры логики. Как дозывается их справедливость?
2. Перечислите следствия из законов алгебры логики.
Все логические операции, которые были рассмотрены в 3.2, распространяются и на функции нескольких переменных. Теперь будем рассматривать функции F(x1, x2,тАж, xn), где xi тАУ логические переменные, которые принимают значения нуля или единицы. Для описания логики функционирования аппаратных и программных средств компьютера используется алгебра логики, или булева алгебра. Два элемента алгебры логики тАУ ее константы тАУ 0 (ложь) и 1 (истина). Во всех компьютерах используются сигналы двух видов. Сигналы можно интерпретировать как двоичные числа, или логические переменные.
Логической функциейF от набора логических переменных х1,тАж, хn называется функция, которая может принимать только два значения: логический 0 и логическая 1.
Область определения логической функции конечна и зависит от количества возможных наборов аргументов. Если тАУ число аргументов, то количество возможных наборов аргументов равно 2n.
Множество значений функции F(x1,тАж, xn) тАУ это множество {0,1}, т. е. F=0 либо 1.
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записываются наборы аргументов, а в правой тАУ соответствующие значения функции.
x1 | x2 | тАж | xn-1 | xn | F(x1, x2,тАж, xn-1, xn) |
| 0 | 0 | тАж | 0 | 0 | F (0,0,тАж, 0,0) |
| 0 | 0 | тАж | 0 | 1 | F (0,0,тАж, 0,1) |
| 0 | 0 | тАж | 1 | 0 | F (0,0,тАж, 1,0) |
| тАж | тАж | тАж | тАж | тАж | тАж |
| 1 | 1 | тАж | 1 | 1 | F (1,1,тАж, 1,1) |
Вектором значений булевой функции F(x1,тАж, xn) называется упорядоченный набор всех значений функции F, при которых значения упорядочены по лексикографическому порядку множества аргументов {0,1}n.
Поскольку всего имеется 2n наборов 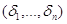 нулей и единиц (|{0,1}n|=2n), существует ровно
нулей и единиц (|{0,1}n|=2n), существует ровно 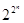 булевых функций F(x1,тАж, xn) от переменных:
булевых функций F(x1,тАж, xn) от переменных:
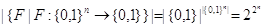 .
.
При =2 количество функций равно 16, при =3 тАУ 256 и т. д. На рис. 3 представлены в упорядоченном виде наборы аргументов для ряда функций тАУ отрицания 0, функций одного, двух и трёх аргументов.
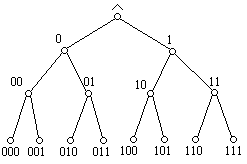
Рис. 3. Упорядоченные наборы аргументов
3.6 Построение формул алгебры логики по заданной таблице истинности
Пусть F тАУ двоичная функция от переменных. Предположим, что F не равна тождественно нулю. Пусть T1, T2,тАж, Tk тАУ все точки ее определения, в которых F=1. Можно доказать, что справедлива следующая формула:
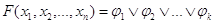 ,
,
где  , j=1,2,тАж, k,
, j=1,2,тАж, k,
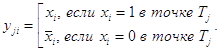
Построить функцию F можно и по-другому. Если функция Fне равна тождественно единице и S1, S2,тАж, Sm тАУ все точки области ее определения, в которых F=0, то справедлива формула:
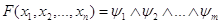 ,
,
где 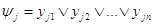 , j=1,2,тАж, m.
, j=1,2,тАж, m.
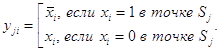
Из приведенных формул видно, что любую двоичную функцию можно записать, используя лишь операции Вм, 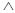 ,
,  .
.
Основная конъюнкция тАУ это конъюнкция основных высказываний переменных или их отрицаний. Например, 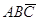 .
.
Основная дизъюнкция тАУ это дизъюнкция основных высказываний переменных или их отрицаний. Например, 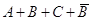 .
.
Конъюнктивной нормальной формой (КНФ) данной формулы называется формула, равносильная данной и представленная в виде конъюнкции основных дизъюнкций. Например, (A+B) (A+C+B) (D+A).
Дизъюнктивной нормальной формой (ДНФ) данной формулы называется формула, равносильная данной и представленная в виде дизъюнкции основных конъюнкций. Например, AB+C+AC.
Теорема 1. Для того чтобы формула алгебры высказываний была тождественно истинной, необходимо и достаточно, чтобы ее КНФ содержала в каждой элементарной дизъюнкции некоторое высказывание и его отрицание.
Теорема 2. Для того чтобы формула алгебры высказываний была тождественно ложной, необходимо и достаточно, чтобы ее ДНФ содержала в каждой элементарной конъюнкции некоторое высказывание и его отрицание.
Совершенные дизъюнктивные, конъюнктивные и полиномиальные нормальные формы представления переключательных (логических) функций. Многообразие формул, посредством которых может быть выражена любая логическая функция, определяет многообразие форм логических функций, т. е. способов их записи путем применения к переменным и их группам элементарных логических операций. Наиболее удобными для практического использования оказываются совершенные нормальные формы представления сложных логических функций. В алгебре логики доказывают, что любая логическая функция F (A, B, C,тАж, N) может быть представлена только одной совершенной дизъюнктивной нормальной формой (кроме константы нуль) или только одной совершенной конъюнктивной нормальной формой (кроме константы единица).
Пусть функция X=F (A, B, C) задана таблицей 4. Запись функции Х в виде логической суммы (дизъюнкции) логических произведений (конъюнкций) переменных, для которых значение функции Х равно 1, и является совершенной дизъюнктивной нормальной формой (СДНФ) представления логической функции.
Таблица 4
| A | B | C | X |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
СДНФ логической функции следует находить в такой последовательности:
1) составить произведения переменных для строк таблицы истинности, в которых Х равна 1. Если значение переменной (А, В или С) в строке равно 0, то в произведении записывается отрицание этой переменной;
2) написать сумму произведений, для которых функция Х равна 1. Полученная сумма и является СДНФ. В общем виде
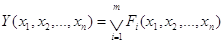 , (1)
, (1)
Это правило называют правилом записи переключательной функции по единицам. Согласно этому правилу, данные табл. 4 описываются аналитическим выражением, связывающим все наборы переменных, для которых Х=1, в виде:
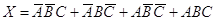 . (2)
. (2)
Запись функции Х в виде логического произведения (конъюнкции) логических сумм (дизъюнкций) переменных, для которых функция Х равна 0, является совершенной конъюнктивной нормальной формой (СКНФ) представления логической функции.
Для табл. 4 аналитическое выражение в СДНФ, связывающее все наборы переменных, для которых Х=0, имеет вид:
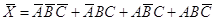 . (3)
. (3)
Для представления логической функции Х в СКНФ произведем операцию отрицания левой и правой частей равенства (3)
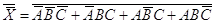
и на основании законов двойного отрицания и инверсии
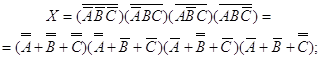
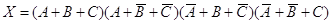 . (4)
. (4)
СКНФ логической функции, согласно (4), следует находить в такой последовательности:
1) составить логические суммы переменных для строк таблицы истинности, в которых функция Х равна 0. Если значение переменной (А, В или С) в строке равно 1, то в сумме записывается отрицание этой переменной;
2) написать логическое произведение составленных логических сумм. Полученное произведение и является СКНФ. В общем виде:
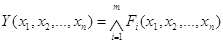 , (5)
, (5)
где Fi тАУ сложные дизъюнкции.
Это правило также называют правилом построения переключательной функции по нулям.
Кроме представления функций в виде СДНФ и СКНФ используют и совершенную полиномиальную нормальную форму СПНФ. Вместо дизъюнкции может быть записана функция сложения по модулю два (сумма Жегалкина):
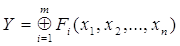 , (6)
, (6)
где Fi тАУ сложные конъюнкции.
Существует специальная таблица, в которой все элементарные логические операции от двух аргументов представлены в двух совершенных нормальных формах.
Нормальные формы представления переключательной функции иногда называют стандартными (табл. 5).
Таблица 5