Вивчення елементiв стереометрii у курсi геометрii 9 класу
ДИПЛОМНА РОБОТА
"Вивчення елементiв стереометрii у курсi геометрii 9 класу"
Вступ
Дитина дуже рано починаi орiiнтуватися в оточуючому ii реальному, а потiм i уявному просторi з урахуванням положення власного тiла. В дослiдженнях А.Я. Колодноi, Б.Г. Ананьiва, А.А. Люблiнськоi, А.Н. Сорокiна i багато iнших показано, що першi просторовi образи у дiтей виникають при усвiдомленнi ними схеми свого тiла, залежно вiд розпiзнавання правоi i лiвоi руки (ноги). Всi предмети в просторi вони сприймають з урахуванням його вертикального положення (вгорi тАУ внизу, спереду тАУ ззаду, збоку, справа тАУ злiва i т. д.). Ця природна позицiя служить для створення рiзноманiтних i адекватних просторових образiв. Орiiнтацiя по схемi тiла i ведучою не тiльки при практичному оволодiннi простором, але i при переходi вiд реального (фiзичного) до уявного (геометричного) простору.
Про це красномовно свiдчать дитячi малюнки. Починаючи малювати, дiти намагаються перш за все вiдтворити в малюнку себе або iнших ВлчоловiчкiвВ». Вiдтворюючи умовними засобами себе в малюнку, вони стараються на цiй основi зробити композицiйну побудову малюнка, тобто здiйснити просторове розмiщення всiх об'iктiв. В молодших класах на уроках малювання учнi малюють спочатку фiгури на площинi, але деякi з них вже стараються надавати iм обтАЩiмного вигляду. Пiзнiше цi фiгури зображають в просторi, не знаючи при цьому, що таке трьохвимiрний простiр. Дiти лiплять обтАЩiмнi фiгури з пластилiну та роблять iх з iнших пiдручних матерiалiв. У старших класах вивчення просторових фiгур вiдбуваiться на уроках стереометрii.
Просторове мислення виникаi в надрах практичноi потреби орiiнтацii на мiсцевостi, серед об'iктiв матерiального свiту. Особливiсть просторових зв'язкiв, як пiдкреслював Ананьiв, полягаi в тому, що це i один з видiв вiддзеркалення вiдношень мiж об'iктами. Це означаi, що просторовi властивостi не данi у всьому своiму рiзноманiттi в окремих статичних, iзольованих предметах, застиглих геометричних формах. Вони можуть бути виявленi, вивченi, використанi лише в ходi активноi перетворюючоi дiяльностi суб'iкта, направленоi на трансформацiю, видозмiну об'iктiв, в ходi якоi тiльки i можуть бути видiленi (знайденi) просторовi властивостi i вiдношення.
Розвиток просторового мисленнями дiтей вiдбуваiться i в процесi навчання. Як вiдомо, якнайповнiше просторовi властивостi i вiдношення дослiджуються в математицi. З одноi сторони, розвиток просторового мислення школярiв i необхiдним для розвитку у них здiбностей до уявлення взагалi, а з другоi тАУ це необхiдна умова для свiдомого засвоiння курсу стереометрii. Формування просторового мислення i одним iз найважливiших завдань геометрii. Багато математикiв працювали над тим, як покращити процес вивчення геометрii, щоб максимально розвинути просторове мислення учнiв.
В даний час ведеться серйозна робота по удосконаленню змiсту освiти i шляхiв навчання з метою максимального iх наближення до сучасного рiвня наукових знань i методiв дослiдження. В зв'язку з цим розробляються психолого-дидактичнi принципи вiдбору навчального матерiалу з урахуванням досягнень науки i технiки, визначаються оптимальнi способи його засвоiння.
На етапi розбудови системи нацiональноi освiти та iнтеграцii ii в свiтову важливим i питання вiдповiдностi змiсту базовоi математичноi освiти вимогам суспiльства, розвитку науки, сучасним потребам особи.
Основна школа в Украiнi згiдно з Законом Украiни ВлПро освiтуВ» повинна забезпечити базову загальну середню освiту, тобто дати випускникам чiтко окреслене коло знань, практичних навичок та умiнь, потрiбних для роботи в умовах сучасного виробництва, а також для здобуття повноi загальноi середньоi освiти в старшiй школi та продовження неперервноi освiти.
Специфiка i структура шкiльного курсу математики вiдкривають широкi можливостi для розвитку творчих здiбностей учнiв, формування прийомiв розумовоi дiяльностi, iнтелекту.
У вирiшеннi цих питань важливе мiсце належить геометрii, оскiльки геометричнi знання i вмiння i одним iз вагомих факторiв, що забезпечують, насамперед, готовнiсть людини до неперервноi освiти та трудовоi дiяльностi.
Оскiльки повна загальна середня освiта в Украiнi i обов'язковою i ii можна здобувати у рiзних типах навчальних закладiв освiти, то частина учнiв пiсля 9 класу продовжуi навчання в загальноосвiтнiй школi, iншi вступають до рiзних училищ, технiкумiв, ПТУ. Для бiльшостi з тих, хто не продовжуi далi навчання в середнiй школi, стереометрiя викладаiться в меншому обсязi, тому залишаються майже незнайомими властивостi просторових фiгур, хоча саме вони i необхiдними людинi в повсякденному життi. Учнi професiйних навчально-виховних закладiв зазнавали труднощiв при вивченнi спецiальних дисциплiн та пiд час виробничоi практики, тому що згiдно з дiючою ранiше програмою в 7тАУ9 класах вони вивчали геометрiю на площинi, тодi як стереометричнi знання та умiння формувалися лише в старшiй школi.
Виходячи з цього, виникаi необхiднiсть деякого перерозподiлу геометричного матерiалу порiвняно з дiючими програмами. Це стосуiться, насамперед, вивчення в курсi геометрii основноi школи на наочно-iнтуiтивному рiвнi таких понять стереометрii, як паралельнiсть i перпендикулярнiсть прямих i площин, прямокутний паралелепiпед, пряма призма, пiрамiда, цилiндр, конус, куля. Поряд з цим мають формуватися практичнi вмiння обчислювати площi поверхонь i об'iми основних геометричних тiл, зображати просторовi фiгури на площинi, будувати iх розгортки, ВлчитатиВ» рисунки.
Саме тому у 2003 роцi, з метою систематизацii деяких знань зi стереометрii у школярiв основноi школи та пiдготовки iх до вивчення цього курсу у старших класах, у програму з математики для девтАЩятого класу введено роздiл ВлПочатковi вiдомостi зi стереометрiiВ».
На даний час практично немаi розроблених методичних матерiалiв, систем задач, якi б вiдповiдали нововведенню. Виникла потреба в створеннi методики вивчення елементiв стереометрii у девтАЩятому класi. Тому тема ВлПро вивчення елементiв стереометрii у курсi геометрii девтАЩятого класуВ» i на сьогоднi актуальною.
Розкриття цiii теми потребуi розвтАЩязання таких задач:
1. Вивчити програму з математики для девтАЩятого класу, а особливо роздiл ВлПочатковi вiдомостi зi стереометрiiВ»; упорядкувати робочу програму вивчення цього матерiалу в девтАЩятому класi.
2. Скласти систему задач до цього роздiлу.
3. Розробити методичнi рекомендацii до вивчення елементiв стереометрii у девтАЩятому класi.
4. Показати дидактичнi можливостi використання ППЗ GRAN-3D при вивченнi елементiв стереометрii у 9 класi.
Робота складаiться з вступу, двох роздiлiв, висновкiв, списку лiтературних джерел i додаткiв.
У першому роздiлi увага зосереджена на метi i завданнi введенню елементiв стереометрii у курсi математики основноi школи. Також вiн присвячений для з'ясування, яка роль i мiсце елементiв стереометрii у розвитку просторового мислення школярiв.
У другому роздiлi розглядаються методичнi рекомендацii вивчення елементiв стереометрii у курсi геометрii 9 класу з врахуванням особливостей нових шкiльних пiдручникiв з геометрii.
1. Елементи стереометрii у шкiльному курсi математики
1.1 Мета i завдання введення елементiв стереометрii у курсi математики основноi школи.
Вирiшальне значення для системи шкiльноi освiти маi формуючий вплив предмета математики на розвиток логiчного мислення, просторових уявлень i уяви, алгоритмiчноi i iнформацiйноi культури, уваги, памтАЩятi.
Характеристика геометрii як науки становить методологiчну основу для проектування шкiльного предмета геометрii i, природно, ведуть до основних завдань навчання геометрii в школi:
1. розвиток образного, зокрема просторового, мислення, розвиток логiчного мислення;
2. формування розумiння вiдношень мiж геометричними обтАЩiктами i обтАЩiктами реального свiту;
3. вмiння застосовувати геометрiю для розвтАЩязування практичних задач.
Вказана вище триiдина мета навчання геометрii i загальновизнаною. Однак ii реалiзацiя на практицi викликаi значнi труднощi. Безумовно, переважна частина цих труднощiв маi обтАЩiктивну природу: складнiсть предмета та складнiсть видiв дiяльностi, якi мають опанувати учнi.
Роздiл ВлПочатковi вiдомостi зi стереометрiiВ» i новим у програмi геометрii в 9-х класах i маi на метi, щоб учнi, якi не будуть продовжувати вивчення геометрii в старших класах, мали уявлення про просторовi фiгури, про обчислення площ поверхонь та обтАЩiмiв простiших геометричних тiл. РЖнше призначення цього роздiлу тАУ пропедевтична пiдготовка до вивчення геометрii в 10 i 11 класах. Основна мета тАУ повторити, привести в систему i розширити вiдомостi про геометричнi фiгури в просторi та навчити обчислювати площi поверхонь i обтАЩiм розглянутих тiл.
Однiiю з основних iдей розбудови математичноi освiти, що записанi в ВлКонцепцii шкiльноi математичноi освiтиВ», i iдея гармонiйного розвитку особистостi, виховання творчих здiбностей людини, здатноi вирiшувати найскладнiшi життiвi проблеми. При цьому перед геометрiiю ставляться важливi завдання з формування мислення, розвитку уяви, просторових уявлень, практичних навичок i умiнь, оскiльки вони i вагомими компонентами загальнолюдськоi культури взагалi.Дiюча система шкiльноi геометричноi освiти не може забезпечити належне виконання цих завдань. Це обумовлено, насамперед, ii будовою.
Курс математики 5тАУ6-х класiв вважаiться пропедевтичним у питаннях вивчення геометрii. Вiн маi за мету сформувати в учнiв елементарнi знання про основнi геометричнi фiгури перед вивченням систематичного курсу геометрii. Таке попереднi вивчення на рiвнi ознайомлення iстотно полегшуi наступне розгортання логiчноi системи знань з дотриманням строгостi доведення. Однак геометрична частина настiльки скорочена, що не даi змоги досягти поставленоi мети навiть за умови, що молодший пiдлiтковий вiк i сприятливим для розвитку образного мислення, просторових уявлень та уяви, вкрай необхiдних для орiiнтацii в середовищi, що нас оточуi, для цiлiсного, багатогранного сприймання дiйсностi.
Систематичний курс геометрii у 7тАУ11-х класах чiтко розмежований. У пiдручнику О.В. Погорiлова ВлГеометрiя 7тАУ11В», за яким донинi навчали геометрii в переважнiй бiльшостi шкiл Украiни, роздiли ВлПланiметрiяВ» та ВлСтереометрiяВ» подаються окремо, причому перша частина ВлПланiметрiяВ» елементiв стереометрii не мiстить. Така штучна й тривала iзоляцiя психiки дитини вiд спiввiдношень реального тривимiрного свiту завдаi значноi шкоди природному розвитку ii просторовоi уяви. Актуальною i потреба перегляду шкiльних програм з математики, зокрема з геометрii. Слiд зазначити, що у цьому напрямку вже намiтилися певнi зрушення.
Так, новi програми з математики для основноi та профiльноi старшоi школи побудованi з урахуванням вимог Державного стандарту базовоi i повноi середньоi освiти, яким передбачено вивчення математики за методом фузiонiзму. Зокрема, курс геометрii основноi школи пропонуiться будувати так, щоб елементи стереометрii тiсно переплiталися з вiдповiдним планiметричним матерiалом, що значно полегшить створення в систематичному курсi стереометрii цiлiсних i мiцних знань, стiйких до збереження в пам'ятi, сприятиме розвитку просторових уявлень та уяви учнiв. Частi переходи вiд двовимiрноi площини до тривимiрного простору сприятимуть розвитку iнтуiцii школяра. Позитивною рисою також i пiдвищена увага до питань пропедевтики геометрii, особливо в 5тАУ6-х кл-х (див. додаток А).
Одночасно з пiдручником геометрii О.В. Погорiлова в 7тАУ9-х класах використовуiться пiдручник геометрii авторського колективу на чолi з Г.П. Бевзом. Вiн у 9-му класi завершуiться роздiлом ВлЕлементи стереометрiiВ». У цьому роздiлi учнiв ознайомлюють з прямими та площинами в просторi, вводять поняття многогранникiв, фiгур обертання, а також пропонують формули площ поверхонь та об'iмiв геометричних тiл. Вивчення даного роздiлу передбачаi виконання практичних завдань з виготовлення моделей многогранникiв, фiгур обертання, розв'язування вправ на обчислення iх площ поверхонь та об'iмiв.
Як бачимо, зрушення щодо введення питань стереометрii в курс математики основноi школи i. Однак питання визначення змiсту i обсягу стереометричного матерiалу в курсi математики основноi школи, його мiсця в програмi, вимог до пiдготовки учнiв пiд час диференцiйованого навчання залишаються розв'язаними недостатньо. Недостатньо розроблена також методика його вивчення та не створена система задач, яка забезпечуi це вивчення.
Виходячи з цiлей i завдань вивчення математики, рекомендованого змiсту питань геометрii, шкiльний курс геометричноi освiти доцiльно будувати так.
5тАУ6-тi класи тАУ курс наочноi геометрii, який по сутi маi бути пропедевтичним перед вивченням систематичних курсiв планiметрii та стереометрii. Саме в цьому полягаi одна з його основних цiлей. Не менш важливим i озброiння учнiв практичними знаннями з геометрii, якi потрiбнi iм пiд час вивчення географii, фiзики, креслення, трудового навчання та iнших сумiжних дисциплiн.
Прiоритетними завданнями мають бути розвиток просторових уявлень та уяви, систематизацiя емпiричного геометричного матерiалу, накопиченого в дошкiльному вiцi та в початкових класах; формування уявлень про певнi класи геометричних фiгур на площинi та в просторi; формування навичок використання формул площ та об'iмiв геометричних фiгур пiд розв'язування задач прикладноi спрямованостi.
Реалiзацiя цих завдань маi здiйснюватися через спостереження геометричних фiгур (зокрема й просторових) в оточуючому середовищi, видiлення iх з цього середовища та манiпулювання ними; використання моделей плоских i просторових фiгур та iх виготовлення; вимiрювання та обчислення за готовими формулами певних геометричних величин; дослiдне встановлення деяких властивостей фiгур, що розглядаються.
Спираючись на Державнi стандарти базовоi та повноi середньоi освiти, доцiльно в змiст даного курсу разом з наявним геометричним матерiалом включити питання стереометрii.
Змiст геометричного матерiалу та вимоги до пiдготовки учнiв подано у таблицi 1 (див. додаток Б).
7тАУ9-й класи тАУ систематичний курс планiметрii, який маi будуватися на основi фузiонiзму, тобто стереометричний матерiал маi органiчно поiднуватися з вiдповiдними поняттями та фактами планiметрii без суттiвих змiн внутрiшньоi логiчноi структури самого курсу. При цьому планiметрiя вивчаiться на систематичному рiвнi в межах iснуючих державних програм, з вiдповiдними обТСрунтуваннями та доведеннями розглядуваних фактiв, стереометрiя тАУ на рiвнi пропедевтики.
Стереометричний матерiал, що вивчаiться у 7тАУ9-х класах, за назвами дещо збiгаiться iз запропонованим у 5тАУ6-х класах, проте змiст понять поступово наповнюiться новими логiко-математичними властивостями, а сформованi образи перетворюються у математичнi поняття, яким потiм даються чiткi означення.
До завдань, що стосуються вивчення стереометричноi частини курсу, належать такi: формування понять про певнi класи многогранникiв, тiл обертання та вивчення деяких iх властивостей; формування вмiнь застосовувати формули площ поверхонь та об'iмiв тiл до розв'язування прикладних задач; формування конструктивних умiнь учнiв, iх графiчноi культури.
Питання стереометрii мають рiвномiрно розглядати у 7тАУ9-х класах, що забезпечить безперервнiсть iх вивчення. Для мiцного та свiдомого засвоiння понять стереометрii слiд якомога ширше використовувати моделi, таблицi, рисунки.
Змiст стереометричного матерiалу в 7тАУ9-х класах та вимоги до пiдготовки учнiв подано у таблицi 2 (див. додаток Б).
10тАУ11-й класи тАУ систематичний курс стереометрii, завдання якого тАУ систематичне вивчення стереометричного матерiалу на глибшому теоретичному рiвнi з повним обТСрунтуванням тверджень, що доводяться.
1.2 Роль i мiсце елементiв стереометрii у розвитку просторового мислення школярiв
1.2.1 Психолого-педагогiчнi особливостi вивчення елементiв стереометрii
Навчання тАУ складний i багатогранний процес. Його основною метою i прагнення дати (або отримати) цiлiсне уявлення про оточуючий матерiальний свiт. Для досягнення цiii мети необхiдно враховувати фiзiологiчнi, психологiчнi та педагогiчнi особливостi цього процесу.
Просторове мислення, як вiдомо, i складовою частиною чуттiво-образного мислення i не i апрiорi визначеним, запрограмованим вiд народження. Воно формуiться в процесi iндивiдуального розвитку людини. Для правильного його формування слiд спиратися насамперед на здобутки в галузi фiзiологii та психологii, зокрема на вiдкриття явища асиметрii пiвкуль головного мозку. Ще порiвняно недавно iснувала думка про iх рiвноправнiсть щодо деяких функцiй. Проте дослiди Р. Сперрi та його послiдовникiв, а також досягнення вiтчизняноi науки переконливо свiдчать про функцiональнi вiдмiнностi пiвкуль головного мозку у сприйняттi образiв реального свiту, формуваннi мислення.
Вiдомо, що лiва пiвкуля керуi роботою правоi частини людського тiла, а права вiдповiдаi за рух лiвих кiнцiвок i чуттiвiсть його лiвоi частини. Крiм того, у лiвiй пiвкулi локалiзованi центри мови, хоча не можна повнiстю виключати здатнiсть правоi пiвкулi розумiти мову. Дослiдження Р. Сперрi показали, що при вiдокремленнi пiвкуль лiва рука, керована правою пiвкулею, здатна вiдтворити показаний рисунок або зобразити куб у трьох вимiрах, тодi як права не може виконати жодну з цих вправ. З цих дослiджень було зроблено припущення, що лiва пiвкуля спецiалiзована на оперуваннi словами та iншими умовними знаками, права ж оперуi образами реальних об'iктiв, вiдповiдаi за орiiнтацiю в просторi.
За допомогою ВллiвопiвкульноiВ» стратегii будь-який матерiал органiзуiться так, що створюiться однозначний контекст, який розумiiться всiма однаково та необхiдний для успiшного спiлкування мiж людьми. Вiдмiнною ж особливiстю ВлправопiвкульноiВ» стратегii i формування багатозначного контексту, який не пiддаiться вичерпному поясненню у традицiйнiй системi спiлкування.
Тому просторово-образне мислення забезпечуi сприйняття реальностi в усiй ii багатогранностi, даi можливiсть орiiнтуватись у просторi багатьох вимiрiв, зокрема в реальному тривимiрному просторi. Стратегiя лiвоi пiвкулi полягаi у здатностi серед багатогранностi зв'язкiв мiж предметами та явищами вiдiбрати основнi, найiстотнiшi.
Сучасна система освiти, зокрема й геометричноi (коли у школi вивчаються два розмежованi курси ВлПланiметрiяВ» та ВлСтереометрiяВ»), спрямована, переважно, на розвиток формально-логiчного мислення, на оволодiння способами побудови однозначного контексту. Можливо, з точки зору дидактики, таке роздiлення й доцiльне, але цим самим ВлзакрiпачуiтьсяВ» образне мислення. Тривалий час плоскi фiгури розглядаються вiдiрвано вiд аналогiчних iм просторових, що створюi штучне обмеження мислення двовимiрним простором i призводить до послаблення просторовоi iнтуiцii, просторових уявлень, стримуi розвиток iнтелектуальних i розумових здiбностей учнiв. РЖ чим бiльше зусиль прикладаiться для того, щоб логiко-знакове мислення було домiнуючим, тим складнiше зламати цей стереотип потiм. Набагато кориснiше та ефективнiше було б спочатку спрямувати бiльше зусиль на формування образного мислення, а потiм, пiд час формування формально-логiчного, на певне обмеження потенцiйних можливостей першого, на його впорядкування. Так само штучне розмежування геометрii на два предмети замiнити систематичним вивченням в основнiй школi курсу планiметрii та елементiв стереометрii.
Формування образного мислення в усiй повнотi та своiрiдностi його функцiй тАУ необхiдна умова ефективного засвоiння знань. Разом з тим це один iз важливих засобiв розвитку особистостi.
Дитина не народжуiться з уже сформованою тiiю чи iншою системою мислення. Його логiчна та образна складовi розвиваються в процесi навчання, виховання залежно вiд того, у якому напрямку цей розвиток спрямовано. Щоб створити сприятливi умови такого розвитку, найперше, мають бути врахованi вiковi особливостi дитини.
Психологи Б.Г. Ананьiв, РД.Ф. Рибалко, В.РЖ. Зикова, Е.А. Фарапонова стверджують: сприйняття простору дiтьми вже у дошкiльному вiцi набуваi певного розвитку. У них формуються елементарнi вмiння орiiнтуватися в навколишньому свiтi, утворюються системи зв'язкiв мiж зоровим, слуховим i руховим аналiзаторами. Так, уже на третьому роцi життя у дитини складаiться системний механiзм просторовоi орiiнтацii. З ii розвитком цей процес збагачуiться новими вiдношеннями та складовими.
Значно якiснiше це сприйняття простору вiдбуваiться у молодшому шкiльному вiцi, оскiльки програмуiться навчанням i керуiться вчителем. Переважна бiльшiсть молодших школярiв здатна ВлуявитиВ» геометричнi тiла (куля, куб, прямокутний паралелепiпед, конус тощо) як реальнi об'iкти, що iм вiдповiдають (м'яч, цеглина, пенал, лiйка тощо). Дiти спроможнi розпiзнати цi тiла на готових моделях, малюнках, назвати iх. У них рано формуiться сприймання зображень просторових фiгур.
РЖ.СЯкиманська, аналiзуючи вiковi вiдмiнностi учнiв, що проявляються пiд час розв'язування задач на просторовi перетворення, видiляi таку особливiсть: просторовi образи молодших школярiв досить рухомi та динамiчнi. У навчальнiй дiяльностi дiти ознайомлюються не тiльки з такими ознаками об'iктiв, як колiр, маса, форма тощо, а й з властивостями, що визначають положення цих об'iктiв у тривимiрному просторi.
Крiм того, за належного навчання дiти легко справляються з завданнями на перетворення елементiв зображення, добре розрiзняють геометричнi форми, з бажанням, залюбки складають розгортки об'iмних предметiв за iх наочним зображенням. Звiдси випливаi потреба у використаннi наочностi пiд час навчання дiтей цього вiку.
З переходом учнiв до середнiх класiв (пiдлiтковий вiк) змiст iх навчальноi дiяльностi ускладнюiться, на основi чого вiдбуваiться дальший розвиток образного мислення. Глибше розумiння учнями властивостей предметiв i явищ навколишнього свiту проявляiться тепер у формуваннi абстрактних понять. З наочно-образного iх мислення поступово стаi абстрактно-понятiйним.
Пiдлiтки, на вiдмiну вiд молодших школярiв, уже вмiють розпiзнавати та видiляти в предметах i явищах тi ознаки, якi iстотнi для даного роду чи виду явищ. Проте варто зазначити, що формування абстрактних понять у цьому вiцi часто зводиться до формального засвоiння властивостей, iх вiдриву вiд конкретних об'iктiв. Тому часто учнi знають визначення, формули i добре оперують ними, та не можуть належно розкрити iх змiст i успiшно застосовувати до розв'язування конкретних задач.
У процесi формального засвоiння знань природна здатнiсть дiтей до динамiзму сприймання витiсняiться установкою на використання однiii, фiксованоi позицii спостереження. Подолати це негативне явище можна включенням дiтей в активну навчальну дiяльнiсть, залученням до виготовлення наочних посiбникiв, зокрема моделей просторових фiгур, iх розгорток з картону, рiзноманiтного пiдручного матерiалу; вимiрювання та обчислення iх розмiрiв, площ поверхонь, об'iмiв. У ходi такоi роботи школярi не тiльки оволодiвають практичними навичками, а й глибше засвоюють змiст понять.
РЖ.С. Якиманська, В.В. Давидов, РД.М. Кабанова-Меллер, Г.С. Костюк, Н.А. Менчинська, РЖ.РД. Унтта та iн. зазначають, що для розвитку просторового мислення недостатньо враховувати лише вiковi особливостi учнiв, необхiдно брати до уваги iх iндивiдуальнi вiдмiнностi.
Учнi одного й того самого вiку помiтно вiдрiзняються один вiд одного за своiми здiбностями до просторового мислення. В одних пiд впливом певних факторiв (iнтерес до технiки, робота з ВлконструкторамиВ», домашнi навчання i виховання та iн.) здатнiсть до просторового мислення формуються ще до початку систематичного вивчення предметiв, якi висувають до нього спецiальнi вимоги. Учитель, який працюi з такими учнями, спираючись на наявнi здiбностi, маi забезпечити подальший розвиток просторового мислення, добираючи завдання вiдповiдно до iндивiдуальних вiдмiнностей. РД учнi, якi з певних причин до цього часу не досягли такого рiвня. Тому перед учителем постаi iнша задача тАУ формувати здiбностi учнiв до просторового мислення. Зрозумiло, що учнi, у яких така здiбнiсть не сформована, не можуть засвоювати знання на однаковому рiвнi з iншими. Тому слiд диференцiювати та iндивiдиалiзувати роботу щодо розвитку наявних здiбностей i щодо iх формування.
В учнiв, якi приступають до вивчення систематичного курсу геометрii, просторовi (тривимiрнi) уявлення розвиненiшi бiльше, нiж двовимiрнi, що недостатньо враховано пiд час складання програми з математики 5тАУ9-х класiв, особливо з курсу геометрii. Багатий досвiд дiтей, накопичений ними у практицi оперування реальними предметами, не знаходить свого безпосереднього застосування та подальшого удосконалення, оскiльки, вивчаючи планiметрiiю, школярi оперують лише площинними зображеннями, тодi як тривимiрнi образи вiдходять на другий план.
Проведенi нами дослiдження переконливо вказують на наявнiсть в учнiв середнiх класiв уявлень про площину (поверхня столу, класноi дошки, пiдлоги, вiкна), паралелепiпед (сiрникова коробка, цеглина), цилiндр (склянка), конус (лiйка), кулю (м'яч, глобус), призму (шестигранний олiвець, намет). Дiти намагаються дати наочне зображення таких фiгур, проте не можуть цього зробити, тому що у них недостатньо сформованi просторовi уявлення, вiдсутнi вiдповiднi навички та вмiння. Основна причина названого явища очевидна. Вона полягаi в тому, що пiд час вивчення планiметрii учнiв привчили мислити ВлплоскимиВ» образами.
Викладенi вище мiркування приводять до загальних висновкiв:
1) iснують як фiзiологiчнi, так i психологiчнi передумови вивчення елементiв стереометрii в курсi математики основноi школи, що не враховуi сучасна система шкiльноi геометричноi освiти, яка, будучи бездоганною з дидактичноi точки зору, не вiдповiдаi перiодам розвитку геометрii як науки (принцип iсторизму) i, певною мiрою, гальмуi розвиток мислення учнiв;
2) i потреба у вивченнi стереометричного матерiалу в основнiй школi, яке доцiльно здiйснювати на наочно-оперативному рiвнi в систематичних курсах математики (5тАУ6-й класи) i планiметрii (7тАУ9-й класи);
3) таке вивчення вимагаi розробки вiдповiдного методичного забезпечення (програми, дидактичнi матерiали, iнформацiйнi технологii тощо).
1.2.2 Мiсце стереометричного матерiалу в курсi математики основноi школи та вимоги до його засвоiння
Структурування навчального матерiалу з геометрii доцiльно здiйснити на основi таких принципiв:
а) у курсi математики в 5тАУ6-х класах треба ознайомити учнiв з основними поняттями геометрii площини та простору на наочно-iнтуiтивному та оперативному рiвнях, формулами для обчислення площ поверхонь та обтАЩiмiв геометричних тiл, готувати учнiв до вивчення систематичного курсу геометрii, сумiжних дисциплiн;
б) систематичне вивчення геометрii маi починатися з 7-го класу курсом планiметрii, який мiстить дещо розширену порiвняно з 5тАУ6-м класами стереометричну частину;
в) стереометричний матерiал маi органiчно поiднуватися з аналогiчним планiметричним матерiалом; властивостi плоских фiгур треба демонструвати на вiдповiдних елементах стереометричних фiгур, розкриваючи тим самим певнi властивостi останнiх;
г) вивчення стереометричного матерiалу в основнiй школi маi носити практичний характер, базуватися переважно на дослiдах, iнтуiцii, експериментi; тим самим буде сформовано необхiдний запас просторових уявлень як основи для вивчення систематичного курсу стереометрii в 10тАУ11-х класах на науково-теоретичному рiвнi;
ТС) курс планiметрii треба завершити узагальнюючим роздiлом ВлЕлементи стереометрiiВ».
Уявлення про мiсце стереометричного матерiалу в курсi математики основноi школи та його структурування даi таблиця 3 (див. додаток В).
Передбачаiться вивчення геометричного матерiалу з рiзним ступенем обТСрунтованостi та повноти. Мiнiмальний рiвень пiдготовки описаний за допомогою завдань вiдповiдно до класу та навчального матерiалу.
Обовязковi результати навчання
5тАУ6-й класи
1. Точка, пряма, площина, промiнь, вiдрiзок.
1. Позначте точку i проведiть через неi три прямi.
2. Проведiть пряму i позначте на нiй точки A, B, C. Назвiть вiдрiзки, що утворилися.
3. Розгляньте рис. 1.
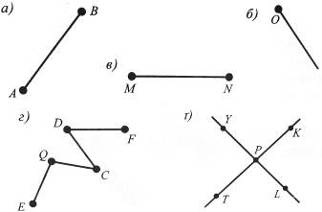
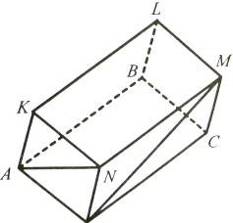
Рис. 1 Рис. 2
Якi фiгури зображено на ньому? Назвiть: три вiдрiзки; три променi. Скiльки прямих зображено на рисунку?
6. Назвiть вiдрiзки i точки, зображенi на рисунку прямокутного паралелепiпеда (рис. 2).
2. Довжина вiдрiзка.
1. Накреслiть пряму i позначте на нiй точки A та B. Вимiряйте вiдрiзок АВ. Запишiть, чому дорiвнюi його довжина.
2. Накреслiть вiдрiзки AB та BC, якщо AB=5 см, BC=4 см 3 мм.
3. Виберiть серед запропонованих моделей модель куба. Вимiряйте та запишiть довжину його ребра в сантиметрах (з точнiстю до десятих).
4. Вимiряйте та запишiть довжини ребер сiрниковоi коробки в сантиметрах (з точнiстю до десятих).
3. Кут та його елементи. Види кутiв.
1. Позначте точку О. Проведiть променi ОА та ОВ. Яка фiгура утворилася? Назвiть ii елементи.
2. Серед оточуючих предметiв назвiть тi, якi мiстять прямий кут.
3. На рис. 3 зображено кути. Назвiть:
а) гострi кути;
б) прямi кути;
в) тупi кути; Рис. 3
г) розгорнутi кути.
4. Побудуйте прямий, гострий i тупий кути. Який з цих кутiв найбiльший (найменший)?
5. За допомогою косинця накреслiть двi прямi, якi при перетинi утворюють прямi кути. На скiльки частин вони дiлять площину? Скiльки розгорнутих кутiв на рисунку?
4. Мiра кута.
1. Вимiряйте кути, зображенi на рис. 3; запишiть результати вимiрювань.
2. Накреслiть кут, градусна мiра якого: а) 65В°; б) 115В°.
3. Якi з кутiв гострi, а якi тупi, якщо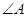 
= 67В°, 
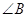=175В°, 
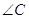=92В°, 
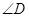=3В°?
5. Паралельнi та перпендикулярнi прямi.
1. На рис. 4 зображено прямi. Якi з них:
а) перетинаються; б) перпендикулярнi; в) паралельнi?
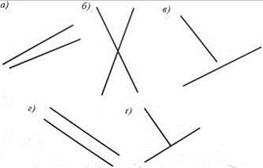
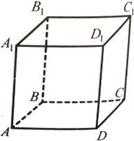
Рис. 4 Рис. 5
2. На оточуючих предметах назвiть (покажiть) елементи, якi мiстять паралельнi та перпендикулярнi прямi.
3. Накреслiть пряму. Поза прямою позначте точку та проведiть через неi за допомогою косинця пряму, перпендикулярну до даноi прямоi.
4. Назвiть у кубi, зображеному на рис. 5:
а) вiдрiзки паралельних прямих;
б) вiдрiзки перпендикулярних прямих.
6. Трикутник i його елементи.
1. Накреслiть трикутник. Назвiть вершини, сторони, кути трикутника.
2. Назвiть трикутники, зображенi на рис. 6.
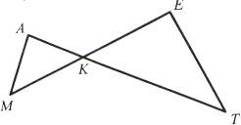
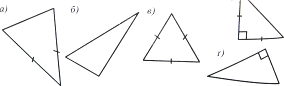
Рис. 6 Рис. 7
3. Назвiть кiлька предметiв, що вас оточують, якi мають форму трикутника.
4. Накреслiть прямокутний, гострокутний, тупокутний трикутники.
5. Накреслiть рiвностороннiй, рiвнобедрений, рiвностороннiй трикутники.
6. Серед трикутникiв, зображених на рис. 7, назвiть:
а) гострокутнi, прямокутнi, тупокутнi;
б) рiзностороннi, рiвнобедренi, рiвностороннi.
7. Накреслiть гострокутний, прямокутний i тупокутний трикутники та проведiть усi iх висоти.
8. Накреслiть довiльний трикутник i вимiряйте його кути. Знайдiть суму цих кутiв.
7. Чотирикутники. Види чотирикутникiв. Прямокутник, квадрат, паралелограм, ромб. Висота паралелограма.
1. Якi iз зображених на рис. 8 фiгур мають форму чотирикутника?
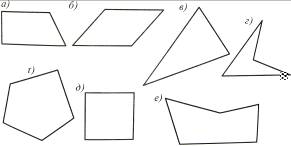
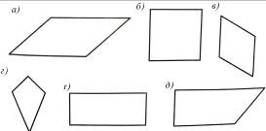
Рис. 8 Рис. 9
2. Серед зображених на рис. 9 фiгур назвiть: а) прямокутник; б) паралелограм.
3. Назвiть кiлька предметiв, що мають форму прямокутника, квадрата.
4. Накреслiть за допомогою косинця та лiнiйки паралелограм ABCD. За допомогою косинця проведiть його висоти з вершини A до сторони CD та з вершини B до сторони AC.
8. Коло. Круг. Круговi дiаграми.
1. Накреслiть коло. Позначте точкою О його центр. Проведiть радiуси ОА та ОВ. Як називають частину кола мiж точками A та B? Як називають частину круга мiж радiусами ОА та ОВ?
2. Назвiть кiлька предметiв, що мають форму: а) кола; б) круга.
3. За допомогою циркуля накреслiть коло радiусом 3 см. Проведiть дiаметр цього кола. Яка його довжина?
9. Довжина кола. Число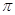 
.
1. Обчислiть довжину кола, радiус якого 2,5 см, вважаючи, що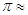 
3,14. Результат округлiть до десятих.
2. Накреслiть довiльне коло. Вимiряйте його радiус i обчислiть довжину кола.
3. Довжина дiаметра земного екватора дорiвнюi 12756 км. Знайдiть довжину екватора, якщо 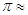3,14. Вiдповiдь округлiть до десяткiв кiлометрiв.
10. Прямi призми: прямокутний паралелепiпед, куб, трикутна призма, прямий паралелепiпед.
1. Серед моделей геометричних тiл знайдiть:
а) прямий паралелепiпед; б) трикутну призму.
2. Серед оточуючих предметiв назвiть тi, що мають форму прямокутного паралелепiпеда. Скiльки граней маi прямокутний паралелепiпед?
3. Серед оточуючих предметiв назвiть тi, що мають форму прямоi трикутноi призми.
4. Виготовiть за готовими розгортками (рис. 10) вiдповiднi фiгури.
5.
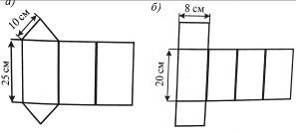
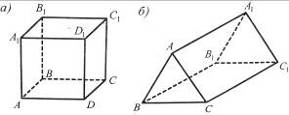
Рис. 10 Рис. 11
6. Якi фiгури зображено на рис. 11?
11. Пiрамiда та ii елементи.
1. Серед даних моделей пiрамiд знайдiть:
а) трикутнi пiрамiди; б) чотирикутнi пiрамiди.
2. Якi геометричнi фiгури i бiчними гранями пiрамiди?
3. Скiльки бiчних граней маi трикутна, чотирикутна, п'ятикутна пiрамiди?
5. Дано модель пiрамiди. Покажiть:
а) основу пiрамiди;
б) бiчнi гранi пiрамiди;
в) вершину пiрамiди.
6. Яку фiгуру зображено на рис. 12? Назвiть:
а) основу зображеноi фiгури;
б) вершину зображеноi фiгури;
в) бiчнi гранi цiii фiгури;
г) ii бiчнi ребра.
12. Цилiндр, конус, куля та iх елементи.
1. Серед даних моделей знайдiть: а) цилiндр; б) конус; в) кулю.
2. Назвiть кiлька предметiв, що мають форму: а) цилiндра; б) конуса; в) кулi.
3. Розгляньте модель цилiндра. Що i його основами? Яка фiгура i бiчною поверхнею цилiндра?
4. На моделi конуса покажiть його основу, вершину, бiчну поверхню.
5. Яку фiгуру зображено на рис. 13? Назвiть:
а) основи фiгури; б) ii твiрну.
6. Назвiть основу, вершину, висоту, твiрну зображеноi на рис. 14 фiгури.
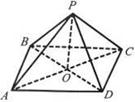
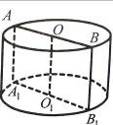
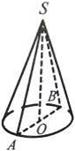
Рис. 12 Рис. 13 Рис. 14
7. Серед даних розгорток (рис. 15) знайдiть: а) розгортку цилiндра; б) розгортку конуса.
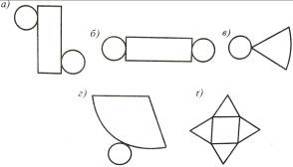
Рис. 15
13. Площа. Одиницi вимiрювання площi.
1. Площа одного квадрата, зображеного на рис. 16, дорiвнюi 1 см2. Яка площа кожноi фiгури, зображеноi на рисунку?
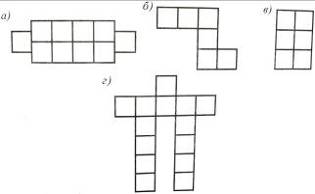
Рис. 16
2. На прямокутнiй дiлянцi зi сторонами 110 м i 75 м скосили траву. З якоi площi скошено траву?
3. Знайдiть площу паралелограма з основою 16 дм i висотою 7 дм, опущеною на цю основу.
4. Знайдiть площу круга радiуса 54 см, вважаючи, що 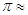3,14. Результат округлiть до десятих.
5. Дiаметр арени цирку 13,6 м. Яку площу маi арена цирку (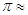3,14)? Результат округлiть до одиниць.
14. Об'iм. Одиницi вимiрювання об'iму.
1. Фiгури на рис. 17 складенi з кубiв, об'iм кожного з яких 1 см3. Знайдiть обтАЩiм кожноi фiгури.
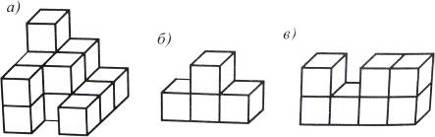
Рис. 17
2. Знайдiть об'iм прямокутного паралелепiпеда, якщо його вимiри дорiвнюють 7 см, 4 см, 3 см.
3. Вимiряйте на моделi прямокутного паралелепiпеда його довжину, ширину та висоту. Обчислiть його об'iм.
4. Знайдiть об'iм кiмнати, якщо ii довжина 5 м, ширина 4 м, висота 3 м.
5. Знайдiть об'iм ями, що маi форму куба, якщо ii глибина 3 м.
6. Знайдiть об'iм призми, основою якоi i прямокутний трикутник з катетами 5 дм i 6 дм. Висота призми дорiвнюi 8,5 дм.
7. Обчислiть об'iм пiрамiди, основою якоi i квадрат зi стороною 7 см. Висота пiрамiди 11
Вместе с этим смотрят:
WEB-дизайн: Flash технологии
РЖiрархiчна структура управлiння фiзичною культурою i спортом в Хмельницькiй областi у м. КамтАЩянець-Подiльському
РЖгровi прийоми навчання на уроках хiмii
РЖгрова дiяльнiсть в групi продовженого дня
РЖдеi народностi педагогiчноi науки та християнськi погляди на виховання у пам'ятках Киiвськоi Русi