Викладення теми "Трикутники" по програмi курсу геометрii в 7 класi середньоi школи
Мiнiстерство освiти i науки Украiни
Днiпропетровський нацiональний унiверситет iм. Олеся Гончара
КУРСОВА РОБОТА
з дисциплiни тАЬМатематикатАЭ
на тему
тАЮВИКЛАДЕННЯ ТЕМИ тАЮТРИКУТНИКИ" ПО ПРОГРАМРЖ КУРСА
ГЕОМЕТРРЖРЗ В 7 КЛАСРЖ СЕРЕДНЬОРЗ ШКОЛИ"
Виконавець: студент групи
Перевiрив:
м. Днiпропетровськ 2010 р.
Анотацiя
Курсова робота на 25 стор.,20 рис., 1 табл., 8 джерел лiтератури.
Систематизований учбовий матерiал викладення теми тАЮТрикутники" по новiй програмi геометрii для 7 класу 12 - рiчноi школи. Наведений перелiк нових пiдручникiв тАЮГеометрiя 7 кластАЭ, якi у 2008 - 2009 роцi створено у вiдповiдностi до Державного стандарту та нових програм з геометрii для 7 класу загальноосвiтнiх навчальних закладiв.
Результати можуть бути використанi в якостi практичного посiбника - конспекта вчителю при викладенi глави тАЮТрикутники" в курсi тАЮГеометрiятАЭ для 7 класу середньоi школи.
The summary
Course work on 25 pages,20 fig., 1 tab., 8 sources of the literature.
The educational material of a statement of a subject тАЮTrianglesтАЭ under the new program of geometry for 7 classes 12 - years schools is systematized. The list of the new tutorials тАЮ Geometry 7 classes тАЭ is given which in 2008 - 2009 are issued according to State standard and new programs on geometry for 7 classes of a school.
The results can be used as the practical grant - abstract to the teacher at a statement of the chapter тАЮTrianglesтАЭ in a rate тАЮGeometry" for 7 classes of a school.
Змiст
Вступ
1. Трикутник i його елементи
2. Ознаки рiвностi трикутникiв
3. Рiвнобедрений трикутник, його властивостi та ознаки
4. Висота, бiсектриса i медiана трикутника
5. Сума кутiв трикутника
6. Властивостi та ознаки рiвностi прямокутних трикутникiв
7. Зовнiшнiй кут трикутника та його властивостi
8. Нерiвнiсть трикутника
Висновки
Список використаноi лiтератури
В курсовiй роботi конспективно викладений теоретичний матерiал теми тАЮТрикутники" в курсi геометрii 7 класу, який згiдно тАЬПрограми для загальноосвiтнiх навчальних закладiв. Математика. 5-12 класи" (видавництво тАЬПерунтАЭ, Киiв, 2005р. - у науково-методичному журналi тАЬМатематика в школi" №2, 2006 р) розподiлений на 3 частини в новiй програмi курсу тАЮГеометрiятАЭ у 7 (введено в 2007/2008 навч. роцi), 8 (введено в 2008/2009 навчальному роцi), 9 (введено в 2009/2010 рр.) класах 12 рiчноi школи.
У 2007 - 2008 навчальному роцi учнi 7х класiв вперше розпочали навчання за новими навчальними планами i програмами 12 рiчноi школи.
Нова програма з геометрii для 7го класу мiстить такi теми: найпростiшi геометричнi фiгури та iх властивостi; взаiмне розташування прямих на площинi; трикутники; коло i круг (геометричнi побудови).
В курсовiй роботi систематизований матерiал викладення теми тАЮТрикутники" по новiй програмi геометрii для 7 класу 12 - рiчноi школи згiдно пiдходу, викладеному в пiдручниках:
тАЬГеометрiя.7 кластАЭ (автори Бевз Г.П., Бевз В.Г., Владiмiрова Н. Г) видавництва тАЬВежатАЭ;
тАЬГеометрiя.7 кластАЭ (автор Апостолова Г. В) видавництва тАЬТРенезатАЭ;
тАЬГеометрiя.7 кластАЭ (автори А.Г. Мерзляк, В.Б. Полонський, М.С. Якiр) видавництва тАЬГiмназiятАЭ.
Цi пiдручники створено у вiдповiдностi до Державного стандарту та нових програм з геометрii для 7 класу загальноосвiтнiх навчальних закладiв.
В роботi використаний графiчний матерiал з посiбникiв:
Погорелов А.В. Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений/ А.В. Погорелов. - 2е изд. - М.: Просвещение, 2001.;
Дергачов В.А. Геометрiя у визначеннях, формулах i таблицях: Довiдковий посiбник для учнiв 7-11 класiв. - X.: Веста: Видавництво тАЮРаноктАЭ, 2006.
Трикутником називаiться фiгура, що складаiться iз трьох точок, що не лежать на однiй прямiй, i трьох вiдрiзкiв, якi попарно сполучають цi точки. Точки називаються вершинами трикутника.
На рисунку 1.1 наведений трикутник з вершинами 
й сторонами 
.
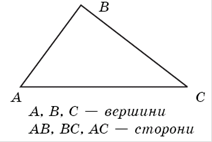
Рис.1.1 Визначення основних елементiв трикутника [5]
Трикутник позначаiться вказiвкою його вершин. Замiсть слова тАЮтрикутник тАЭ iнодi вживають знак 
. Наприклад, трикутник на рисунку 1.2 позначаiться так: 
.
Рис.1.2 Трикутник та визначення кутiв Ða, Ðb, Ðg при його вершинах А, В, С [5]
Кутом трикутника 
при вершинi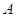 
називаiться кут Ða, утворений напiвпрямим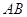и 
й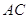 
(див. рис.1.2). Так само визначаються кути трикутника при вершинах 
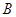i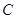 
.
Два вiдрiзки називаються рiвними, якщо вони мають однакову довжину. Два кути називаються рiвними, якщо вони мають однакову кутову мiру в градусах.
Трикутники називаються рiвними, якщо в них вiдповiднi сторони й вiдповiднi кути рiвнi. При цьому вiдповiднi кути повиннi лежати проти вiдповiдних сторiн.
На рисунку 1.3 два рiвних трикутники й 
.
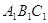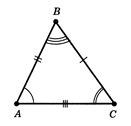
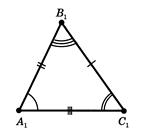
Рис. 1.3 До визначення рiвностi трикутникiв [8]
У них
На кресленнi вiдрiзки звичайно вiдзначають однiiю, двома або трьома рисками, а рiвнi кути - однiii, двома або трьома дужками (див. рис.1.3).
Для позначення рiвностi трикутникiв використовуiться звичайний знак рiвностi: =. Запис D: =D читаiться так: тАЮТрикутник дорiвнюi трикутнику ". При цьому маi значення порядок, у якому записуються вершини трикутника. Рiвнiсть =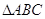
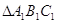означаi, що
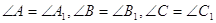. А рiвнiсть =
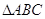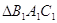означаi вже зовсiм iнше: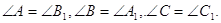 
Задача 1.1 Трикутники i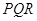 
рiвнi. Вiдомо, що сторона 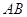дорiвнюi 
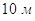, а кут Ð 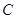дорiвнюi 
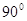. Чому рiвна сторона 
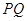й кут Ð
?
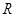РозвтАЩязок. Тому що трикутники й 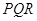рiвнi, то в них 
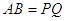, ÐC=ÐR. Виходить, 
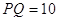м, ÐR=900.
Теорема 2.1 (Перша ознака рiвностi трикутникiв по двох сторонах i куту мiж ними). Якщо двi сторони й кут мiж ними одного трикутника рiвнi вiдповiдно двом сторонам i куту мiж ними iншого трикутника, то такi трикутники рiвнi.
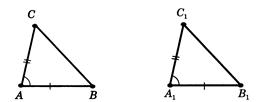
Рис.2.1 До теореми 2.1 (ознака рiвностi трикутникiв по двох сторонах i куту мiж ними) [8]
Доведення.
Нехай у трикутникiв й - двi сторони та кут мiж ними рiвнi: 
(див. рис.2.1). Доведемо, що трикутники рiвнi.
Нехай 
- трикутник, дорiвнюi трикутнику , з вершиною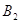 
на променi 
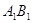й вершиною 
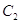в тiй же напiвплощинi вiдносно прямiй 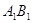, де лежить вершина 
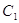(рисунок 2.2, а).
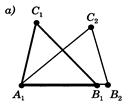
Рис.2.2, а) До доведення 1 признаку рiвностi трикутникiв [8]
Тому що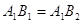 
, то вершина 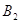збiгаiться з вершиною 
(див. рис.2.2, б).
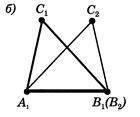
Рис.2.2, б) До доведення 1 признаку рiвностi трикутникiв [8]
Тому що 
то промiнь 
збiгаiться iз променем 
(див. рис.2.2, в).
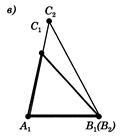
Рис. .2.2, в) До доведення 1 признаку рiвностi трикутникiв [8]
Тому що =, то вершина 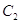збiгаiться з вершиною 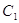(рис.2.2, г).
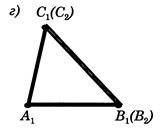
Рис.2.2, г) До доведення 1 признаку рiвностi трикутникiв [8]
Отже, трикутник 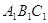збiгаiться iз трикутником 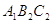, виходить, дорiвнюi трикутнику .
Теорема доведена.
Теорема 2.2 (Друга ознака рiвностi трикутникiв по сторонi й прилеглим до неi кутам).
Якщо сторона й прилеглi до неi кути одного трикутника рiвнi вiдповiдно сторонi й прилеглим до неi кутам iншого трикутника, то такi трикутники рiвнi.
Доведення.
Нехай i 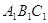- два трикутники, у яких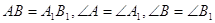 
(рисунок 2.3).
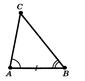
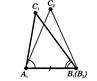
Рис.2.3 До доведення 2i ознаки рiвностi трикутникiв [8]
Доведемо, що трикутники рiвнi. Ð
Нехай 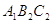- трикутник, дорiвнюi трикутнику з вершиною 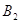на променi 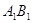й вершиною 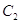в тiй же напiвплощинi вiдносно прямiй 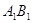, де лежить вершина .
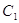Тому що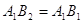 
, то вершина 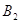збiгаiться з вершиною 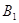. Тому що 
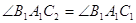й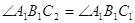 
, то промiнь 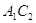збiгаiться iз променем 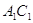, а промiнь 
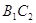збiгаiться iз променем 
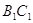. Звiдси витiкаi, що вершина 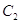збiгаiться з вершиною .
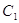Отже, трикутник 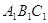збiгаiться iз трикутником 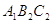, а виходить, дорiвнюi трикутнику .
Теорема доведена.
Теорема 2.3 (Третя ознака рiвностi трикутникiв по трьох сторонах).
Якщо три сторони одного трикутника рiвнi вiдповiдно трьом сторонам iншого трикутника, то такi трикутники рiвнi.
Доведення.
Нехай i 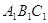два трикутники, у яких 
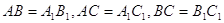. Потрiбно довести, що трикутники рiвнi.
Допустимо, трикутники не рiвнi. Тодi в них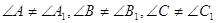 
. РЖнакше вони були б рiвнi по першiй ознацi.
Нехай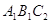 
- трикутник, дорiвнюi трикутнику , у якого вершина лежить в однiй напiвплощинi з вершиною вiдносно прямiй (рисунок 2.4).
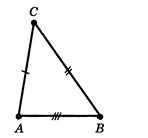
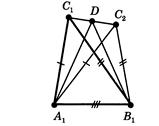
Рис.2.4 До доведення 3 признаку рiвностi трикутникiв [8]
Нехай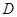 
середина вiдрiзка 
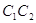й 
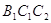- рiвнобедренi iз загальною основою 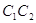. Тому iхнi медiан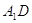и 
й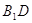 
перпендикуляри прямоi 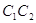. Прямi 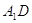й 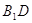не збiгаються, тому що точки
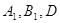не лежать на однiй прямiй. Але через точку 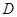прямоi 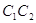можна провести тiльки одну перпендикулярну iй пряму. Ми прийшли до протирiччя
Теорема доведена.
Задача 2.1 Вiдрiзк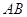и й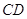 
перетинаються в точцi 
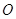, що i серединою кожного з них. Чому дорiвнюi вiдрiзок 
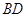, якщо вiдрiзок 
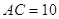м?
РозвтАЩязок. Трикутник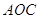и 
й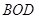 
рiвнi по першiй ознацi рiвностi трикутникiв (рисунок 2.5).
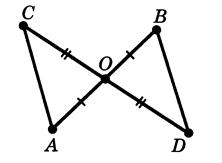
Рис.2.5 До задачi 2.1 [8]
У них кути й рiвнi як вертикальнi, а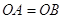 
й 
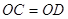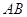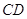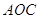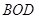тому, що точка i серединою вiдрiзкiв i . З рiвностi трикутникiв i треба рiвнiсть iхнiх сторiн 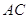i 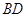. А тому що за умовою задачi 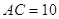м, те й 
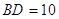м.
Задача 2.2 У трикутникiв i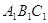 
. Доведiть, що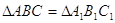 
.
РозвтАЩязок. Нехай i 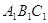данi трикутники (рисунок 2.6).
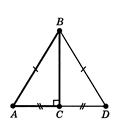
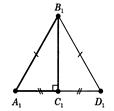
Рис.2.6 До задачi 2.2 [8]
Побудуiмо трикутник 
, який дорiвнюi трикутнику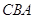 
, i трикутник 
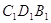, який дорiвнюi трикутнику 
.
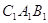Трикутник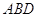и 
й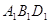 
рiвнi по третiй ознацi. У них 
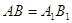за умовою задачi; 
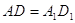тому що 
; 
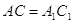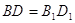, тому що 
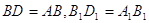. З рiвностi трикутникiв 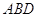i 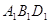треба рiвнiсть кутiв 
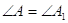. Тому що за умовою 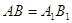,,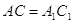 а 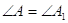, по доведеному, то трикутники й 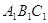рiвнi по першiй ознацi.
Трикутник називаiться рiвнобедреним, якщо в нього двi сторони рiвнi. Цi рiвнi сторони називаються бiчними сторонами, а третя сторона називаiться основою трикутника.
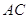На рисунку 3.1 зображений рiвнобедрений трикутник . У нього бiчнi сторони й 
, а основа.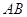
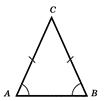
Рис.3.1 До визначення рiвнобедреного трикутника [8]
Теорема 3.1 (властивiсть кутiв рiвнобедренного трикутника)
В рiвнобедренному трикутнику кути при основi рiвнi.
Доведення.
Нехай - рiвнобедрений трикутник з основою 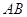(див. рис.3.2). Доведемо, що в нього 
.
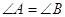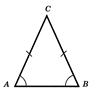
Рис.3.2 До доведення теореми 3.1 [8]
Трикутник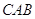 
дорiвнюi трикутнику 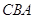по першiй ознацi рiвностi трикутникiв. Дiйсно, 
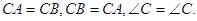З рiвностi трикутника треба, що .
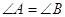Теорема доведена.
Трикутник, у якого всi сторони рiвнi, називаiться рiвностороннiм.
Теорема 3.2 (ознака рiвнобедреного трикутника).
Якщо в трикутнику два кути рiвнi, то вiн рiвнобедрений.
Доведення. Нехай - трикутник, у якому 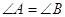(рисунок 3.3).
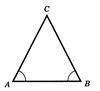
Рис. 3.3 До доведення теореми 3.2 [8]
Доведемо, що вiн рiвнобедрений з основою .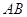
Трикутник дорiвнюi трикутнику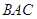 
по другiй ознацi рiвностi трикутникiв. Дiйсно, 
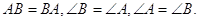З рiвностi трикутникiв треба, що 
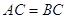. Виходить, по визначенню трикутник рiвнобедрений.
Теорема доведена.
Теорема (3.2) називаiться зворотньою теоремi (3.1). Висновок теореми (3.1) i умовою теореми (3.2). А умова теореми (3.1) i висновком теореми (3.2). Не всяка теорема маi зворотну, тобто якщо дана теорема вiрна, те зворотна теорема може бути невiрна.
Теорема 3.3 (властивiсть медiани рiвнобедреного трикутника).
У рiвнобедреному трикутнику медiана, проведена до основи, i бiсектрисою й висотою.
Доведення. Нехай - даний рiвнобедрений трикутник з основою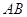 й 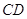- медiана, проведена до основи (рисунок 3.4)
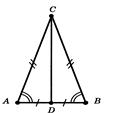
Рис.3.4 До доведення теореми 3.3 [8]
Трикутник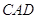и 
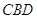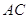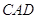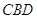й рiвнi по першiй ознацi рiвностi трикутникiв. (У них сторони й рiвнi, тому що трикутник рiвнобедрений. Кути Ð й Ð рiвнi як кути при пiдставi рiвнобедреного трикутника. Сторон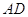и 
й 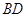рiвнi, тому що 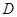- середина вiдрiзка )
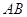З рiвностi трикутникiв витiкаi рiвнiсть кутiв: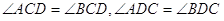 
. Тому що кут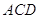и Ð
й Ð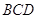
сумiжнi й рiвнi, те 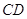- бiсектриса. Тому що кут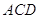и Ð й Ð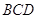 сумiжнi й рiвнi, то вони прямi, тому 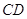висота трикутника.
Теорема доведена.
Задача 3.1 Доведiть, що в рiвностороннього трикутника всi кути рiвнi.
Рiшення. Нехай - даний трикутник з рiвними сторонами: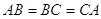 
(рисунок 3.5).
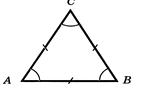
Рис.3.5 До задачi 3.1 [8]
Тому що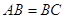 
, то цей трикутник рiвнобедрений з основою 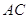. По теоремi 3.1 
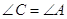. Тому що 
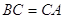, то трикутник рiвнобедрений з основою 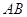. По теоремi 3.1 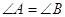. Таким чином, 
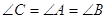, тобто всi кути трикутника рiвнi.
Задача 3.2 Сформулюйте й доведiть теорему, зворотну твердженню задачi 3.1
РозвтАЩязок. У задачi 3.1 умова полягаi в тому, що трикутник рiвностороннiй, а висновок - у тiм, що всi кути трикутника рiвнi. Тому зворотна теорема повинна формулюватися так: якщо в трикутника всi кути рiвнi, то вiн рiвностороннiй.
Доведемо цю теорему. Нехай - трикутник з рiвними кутами: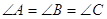 
. Тому що 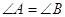, то по теоремi 3.2 
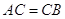. Тому що 
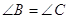, те по теоремi 3.2 
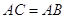. Таким чином
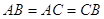, тобто всi сторони трикутника рiвнi. Виходить, по визначенню трикутник рiвностороннiй. Задача 3.3 Доведiть, що бiсектриса рiвнобедреного трикутника, проведена з вершини, протилежнiй основi, i медiаною й висотою. РозвтАЩязок. Нехай - рiвнобедрений трикутник з основою 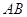i 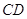його бiсектрисою (рисунок 3.6).
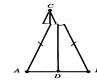
Рис. 3.6. До задачi 3.3 [8]
Трикутник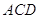и й 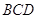рiвнi по першiй ознацi. У них сторона 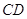загальна, сторони 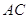й рiвнi як бiчнi сторони рiвнобедреного трикутника, а кути при вершинi 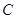рiвнi, тому що 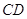- бiсектриса. З рiвностi трикутникiв витiкаi рiвнiсть iхнiх сторiн 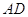i 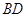. Виходить, 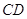- медiана трикутника . А по властивостi медiани рiвнобедреного трикутника вона i й висотою.
Визначення. Висотою трикутника, опущеноi з даноi вершини, називаiться перпендикуляр, проведений iз цiii вершини до прямоi, що мiстить протилежну сторону трикутника. (рисунок 4.1)
Рис.4.1 До визначення висоти трикутника (можливi випадки побудови висоти трикутника) [5]
Визначення. Бiсектрисою трикутника, проведеноi з даноi вершини, називаiться вiдрiзок бiсектриси кута трикутника, яка подiляi кут при вершинi на два рiвнi кути та з'iднуi цю вершину iз крапкою на протилежнiй сторонi (рисунок 4.2).
Визначення. Медiаною трикутника, проведеною з даноi вершини, називаiться вiдрiзок, що з'iднуi цю вершину iз серединою протилежноi сторони трикутника (рисунок 4.2).
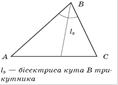
Рис.4.2 До визначення бiсектриси та медiани трикутника [5]
Теорема 5.1. Сума кутiв трикутника дорiвнюi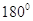 
.
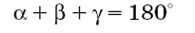
Рис.5.1. Визначення суми кутiв трикутника [5]
Доведення.
Нехай - даний трикутник. Проведемо через вершину пряму, паралельну прямiй . Вiдзначимо на нiй точку так, щоб точки й лежали по рiзнi сторони вiд прямiй (рисунок 5.2).
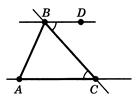
Рис. 5.2. До доведення теореми 5.1 [8]
Кути Ð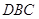
й Ð
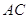рiвнi як внутрiшнi навхрест лежачi, утворенi сiчною з паралельними прямими й 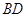. Тому сума кутiв трикутника при вершинах 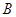i 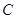дорiвнюi куту Ð.
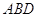А сума всiх трьох кутiв трикутника дорiвнюi сумi кутiв 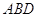i 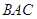. Тому що цi кути внутрiшнi однобiчнi для паралельних 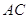i 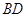й сiчнiй 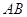, то iхня сума дорiвнюi .
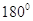Теорема доведена.
З теореми 5.1 витiкаi, що в будь-якого трикутнику хоча б два кути гострi.
Дiйсно, допустимо, що в трикутника тiльки один гострий кут або взагалi немаi гострих кутiв. Тодi в цього трикутника i два кути, кожний з яких не менше 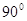. Сума цих двох кутiв уже не менше 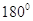. А це неможливо, тому що сума всiх кутiв трикутника дорiвнюi 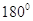. Що й було потрiбно довести.
Трикутник називаiться прямокутним, якщо в нього i прямий кут.
Тому що сума кутiв трикутника дорiвнюi 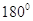, то в прямокутного трикутника тiльки один прямий кут.д.ва iнших кути прямокутного трикутника гострi. Сума гострих кутiв прямокутного трикутника дорiвнюi 
.
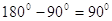Сторона прямокутного трикутника, протилежна прямому куту, називаiться гiпотенузою, двi iншi сторони називаються катетами (рисунок 6.1).
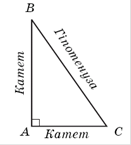
Рис.6.1. До визначення прямокутного трикутника [5]
Вiдзначимо наступну ознаку рiвностi прямокутних трикутникiв по гiпотенузi й катету. Якщо гiпотенуза й катет одного прямокутного трикутника вiдповiдно дорiвнюють гiпотенузi й катету iншого трикутника, то такi трикутники рiвнi (див. рисунок 6.2).
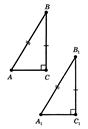
Рис.6.2. До визначення рiвностi прямокутних трикутникiв [8]
Задача 6.1. Доведiть, що в прямокутному трикутнику з кутом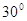 
катет, протилежний цьому куту, дорiвнюi половинi гiпотенузи.
Рiшення. Нехай - прямокутний трикутник iз прямим кутом 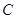i кутом 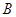, рiвним 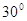(рисунок 6.3).
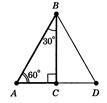
Рис.6.3. До задачi 6.3 [8]
Побудуiмо трикутник 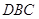, який дорiвнюi трикутнику , як показано на Рис.6.3.
У трикутника 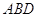всi кути рiвнi 
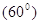, тому вiн рiвностороннiй. Тому що 
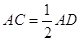, а 
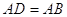, то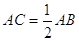 
. Що й було потрiбно довести.
Зовнiшнiм кутом трикутника при данiй вершинi називаiться кут, сумiжний з кутом трикутника при цiй вершинi (рисунок 7.1).
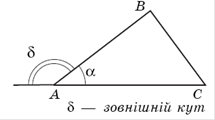
Рис.7.1. До визначення зовнiшнього кута трикутника [5]
Щоб не плутати кут трикутника при данiй вершинi iз зовнiшнiм кутом при цiй же вершинi, його iнодi називають внутрiшнiм кутом.
Теорема 7.1. Зовнiшнiй кут трикутника дорiвнюi сумi двох внутрiшнiх кутiв не сумiжних з ним.
Доведення.
Нехай - даний трикутник (рисунок 7.2).
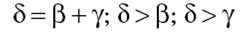
Рис.7.2. До теореми 7.1 [5]
По теоремi про суму кутiв трикутника
.
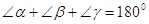Звiдси витiкаi, що
.
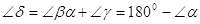У правiй частинi цiii рiвностi стоiть градусна мiра зовнiшнього кута d трикутника.
Теорема доведена.
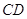З теореми 7.1 витiкаi, що зовнiшнiй кут трикутника бiльше будь-якого внутрiшнього кута, не сумiжного з ним. Задача 7.1. У трикутнику проведена висота . Яка iз трьох точок 
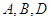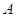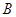лежить мiж двома точками, якщо кути й трикутника гострi? Рiшення. Точка 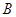не може лежати мiж точкам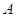и й 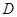(рисунок 7.3),
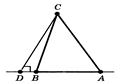
Рис. .7.3. До задачi 7.1 [8]
то гострий кут як зовнiшнiй кут трикутника 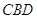був би бiльше прямого кута 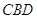. Точно так само доводиться, що й точка 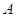не може лежати мiж точкам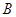и й 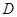. Виходить, точка 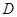лежить мiж точками й .
Якщо точки й рiзнi, то вiдстанню мiж ними називаiться довжина вiдрiзку 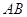. Якщо точк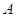и й 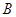збiгаються, то вiдстань мiж ними приймаiться рiвною нулю.
Теорема 8.1 (нерiвнiсть трикутника).
Якi б не були три точки, вiдстань мiж будь-якими двома iз цих точок не бiльше суми вiдстаней вiд них до третьоi точки.
Це значить, що кожна iз цих вiдстаней менше або дорiвнюi суми двох iнших.
Доведення.
Нехай - три данi точки. Якщо двi точки iз трьох або всi три точки збiгаються, то твердження теореми очевидно.
Якщо всi точки рiзнi й лежать на однiй прямiй, то одна з них лежить мiж двома iншими, наприклад 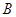. У цьому випадку 
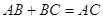. Звiдси видно, що кожне iз трьох вiдстаней не бiльше суми двох iнших.
Допустимо тепер, що точки не лежать на однiй прямiй (рисунок 8.1).
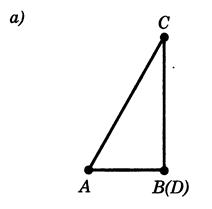
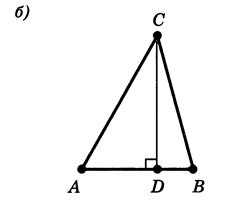
Рис.8.1. До доведення нерiвностей в трикутнику [8]
Доведемо, що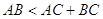 
. Опустимо перпендикуляр 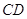на пряму 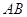. По доведеному 
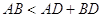. РЖ тому що 
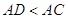й 
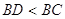, те .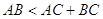
Теорема доведена.
Помiтимо, що у випадку, коли точки не лежать на однiй прямiй, у нерiвностi трикутника строга нерiвнiсть. Звiдси витiкаi, що в будь-якому трикутнику кожна сторона менше суми двох iнших сторiн.
Задача 8.1. Доведiть, що будь-яка хорда окружностi не бiльше дiаметра й дорiвнюi дiаметру тiльки тодi, коли сама i дiаметром.
РозвтАЩязок (рисунок 8.2).
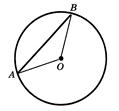
Рис.8.2. До задачi 8.1 [8]
По нерiвностi трикутника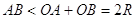 
, причому якщо центр 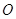не лежить на вiдрiзку 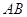, то нерiвнiсть строга. Рiвнiсть маi мiсце тiльки у випадку, коли хорда проходить через центр, тобто i дiаметром.
У 2007-2008 навчальному роцi учнi 7х класiв вперше розпочали навчання за новими навчальними планами i програмами 12 рiчноi школи. Новими навчальними планами передбачено, що в 7 9 класах вивчатиметься два математичнi курси: алгебра i геометрiя.
Кiлькiсть годин на вивчення геометрii не змiнилась i складаi 1,5 години на тиждень. За новою програмою курс геометрii будуiться на досвiдно-дедуктивнiй основi. Основнi геометричнi поняття запозичуються з досвiду, а теореми доводяться дедуктивно з використанням неповноi системи аксiом. Основний апарат доведення - ознаки рiвностi трикутникiв i метод доведення вiд супротивного.
7 клас - Геометрiя (1 год на тиждень у РЖ семестр - 16 год, 2 год на тиждень у РЖРЖ семестрi - 38 год, всього 54 год)
| № п/п | Назва теми | Кiлькiсть годин | Кiлькiсть тематичних оцiнювань |
| I | Найпростiшi геометричнi фiгури та iх властивостi | 4 | дiагностичне |
| II | Взаiмне розташування прямих на площинi | 12 | 1 |
| III | Трикутники | 18 | 1-2 |
| РЖV | Коло i круг. Геометричнi побудови | 14 | 1 |
| V | Повторення i систематизацiя навчального матерiалу | 6 | 1 |
Вместе с этим смотрят:
WEB-дизайн: Flash технологии
РЖiрархiчна структура управлiння фiзичною культурою i спортом в Хмельницькiй областi у м. КамтАЩянець-Подiльському
РЖгровi прийоми навчання на уроках хiмii
РЖгрова дiяльнiсть в групi продовженого дня
РЖдеi народностi педагогiчноi науки та християнськi погляди на виховання у пам'ятках Киiвськоi Русi