Задачи линейной алгебры. Понятие матрицы. Виды матриц. Операции с матрицами. Решение задач на преобразование матриц
Министерство науки и образования Украины
ДГМА
Реферат
на тему:
Задачи линейной алгебры. Понятие матрицы. Виды матриц. Операции с матрицами. Решение задач на преобразование матриц.
Подготовил
учащийся 1КД гр.
Сергей Шрам
Краматорск
2003
Задачи линейной алгебры. Понятие матрицы. Виды матриц. Операции с матрицами. Решение задач на преобразование матриц.
При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи.
Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество п столбцов. Числа т и п называются порядками матрицы. В случае, если т = п, матрица называется квадратной, а число m = тАФ ее порядком.
В дальнейшем для записи матриц будут применяться либо сдвоенные черточки, либо круглые скобки:
или 
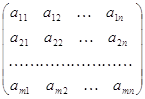
Для краткого обозначения матрицы часто будет использоваться либо одна большая латинская буква (например, A), либо символ aij , а иногда с разъяснением: А = aij = ( aij), где (i = 1, 2, .., т, j=1, 2, .., ).
Числа aij, входящие в состав данной матрицы, называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j тАФ номер столбца. В случае квадрат-ной матрицы
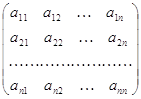(1.1)
вводятся понятия главной и побочной диагоналей. Главной диагональю матрицы (1.1) называется диагональ а11 а12 тАжann идущая из левого верхнего угла этой матрицы в правый нижний ее угол. Побочной диагональю той же матрицы называВнется диагональ аn1 а(n-1)2 тАж a1n, идущая из левого нижнего угла в правый верхний угол.
Основные операции над матрицами и их свойства.
Прежде всего, договоримся считать две матрицы равными, если эти матрицы имеют одинаковые порядки и все их соответствующие элементы совпадают.
Перейдем к определению основных операции над матрицами.
Сложение матриц. Суммой двух матриц A = || aij|| , где (i = 1, 2, .., т, j=1, 2, .., ) и В = || ij|| , где (i = 1, 2, .., т, j=1, 2, .., ) одних и тех же порядков т и п называется матрица С = cij|| (i =1,2, .., т; j = 1, 2, .., п) тех же порядков т и п, элементы сij которой определяются по формуле
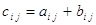, где (i = 1, 2, .., т, j=1, 2, .., ) (1.2)
Для обозначения суммы двух матриц используется запись С = А + В. Операция составления суммы матриц называется их сложением. Итак, по определению:
+ 
= 
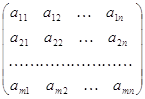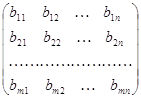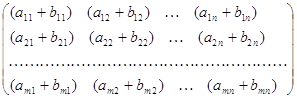
Из определения суммы матриц, а точнее из формул (1.2) непосредственно вытекает, что операция сложения матриц обладает теми же свойствами, что и операция сложения веществен-ных чисел, а именно:
1) переместительным свойством: А + В = В + А,
2) сочетательным свойством: (A + B) + С = А + (В + С).
Эти свойства позволяют не заботиться о порядке следования слагаемых матриц при сложении двух или большего числа матриц.
Умножение матрицы на число. Произведением матрицы A = || a ij|| , где (i = 1, 2, .., m, j=1, 2, .., n) на вещественное число l, называется матрица С = || cij|| (i =1,2, .., m; j = 1, 2, .., ), элементы которой определяются по формуле:
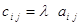, где (i = 1, 2, .., т, j=1, 2, .., ) (1.3)
Для обозначения произведения матрицыi на число используется запись С = lA или С = А l. Операция составления произВнведения матрицы на число называется умножением матрицы на это число.
Непосредственно из формулы (1.3) ясно, что умножение матрицы на число обладает следующими свойствами:
1) сочетательным свойством относительно числового множителя: ( lm ) A = l ( mA );
2) распределительным свойством относительно суммы матриц: l (A + B) = lA + lB
3) распределительным свойством относительно суммы чисел: (l + m) A = lA + mA
Замечание. Разностью двух матриц А и В одинаковых порядков т и п естественно назвать такую матрицу С тех же порядков т и п, которая в сумме с матрицей B дает матрицу A. Для обозначения разности двух матриц используется естественная запись: С = A тАФ В.
Очень легко убедиться в том, что разность С двух матриц А и В может быть получена по правилу С = A + (тАУ1) В.
Произведение матриц или перемножение матриц.
Произведением матрицы A = || aij|| , где (i = 1, 2, .., m, j = 1, 2, .., ) имеющей поВнрядки, соответственно равные т и , на матрицу В = || ij|| , где (i = 1, 2, .., , j=1, 2, ..,р), имеющую порядки, соответственно равные и р, называется матрица С = || cij|| (i =1,2, .., m; j = 1, 2, .., р), имеющая порядки, соответственно равные т и р элементы которой определя-ются по формуле:
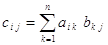где (i = 1, 2, .., m, j = 1, 2, .., p) (1.4)
Для обозначения произведения матрицыi А на матрицу В используют запись С = А × В. Операция составления произведения матрицы А на матрицу В называется перемножением этих матриц.
Из сформулированного выше определения вытекает, что матрицу А можно умножить не на всякую матрицу В, необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В.
Формула (1.4) представляет собой правило составления элементов матрицы С, являющейся произведением матрицы А на матрицу В. Это правило можно сформулировать и словесно: элемент cij стоящий на пвресечении i-й строки и j-го столбца матрицьi С = А В, равен сумме попарных произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.
В качестве примера применения указанного правила приведем формулу перемножения квадратных матриц второго порядка.
×
= 
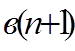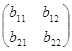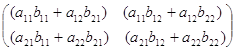
Из формулы (1.4) вытекают следующие свойства произведения матрицы А на матри-цу В:
1) сочетательное свойство: ( А В ) С = А ( В С );
2) распределительное относительно суммы матриц свойство:
( A + B ) С = А С + В С или A ( В + С ) = A В + А С.
Вопрос о перестановочном (переместительном) свойстве произведения матрицы A на матрицу В имеет смысл ставить лишь для квадратных матриц A и В одинакового порядка.
Приведем важные частные случаи матриц, для которых справедливо и переста-новочное свойство. Две матрицы для произведения которых справедливо перестановочное свойство, принято називать коммутирующими.
Среди квадратных матриц выделим класс так называемых диагональных матриц, у каждой из которых элементы, расположенные вне главной диагонали, равны нулю. Каждая диа-гональная матрица порядка п имеет вид
D =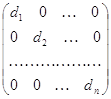 
(1.5)
где d1 , d2 , тАж, dnтАФкакие угодно числа. Легко видеть, что если все эти числа равны между собой, т. е. d1 = d2 = тАж =dn то для любой квадратной матрицы А порядка п справедливо равенство АD=DА.
Среди всех диагональных матриц (1.5) с совпадающими элементами d1 = d2 = тАж =dn= = d особо важную роль играют две матрицы. Первая из этих матриц получается при d = 1, называется единичной матрицей -го порядка и обозначается символом Е. Вторая матрица получается при d = 0, называется нулевой матрицей -го порядка и обозначается символом O. Таким образом,
E =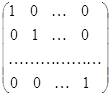 
O =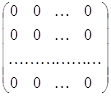 
В силу доказанного выше А Е = Е А и А О = О А. Более того, легко показать, что
А Е = Е А = А, А О = О А = 0. (1.6)
Первая из формул (1.6) характеризует особую роль единичной матрицы Е, аналогичную той роли, которую играет число 1 при перемножений вещественных чисел. Что же касается особой роли нулевой матрицы О, то ее выявляет не только вторая из формул (1.7), но и элементарно проверяемое равенство
А + 0 = 0 + А = А.
В заключение заметим, что понятие нулевой матрицы можно вводить и для неквадрат-ных матриц (нулевой называют любую матрицу, все элементы которой равныi нулю).
Блочные матрицы
Предположим, что некоторая матрица A = || aijпри помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых представляет собой матрицу меньших размеров и называется блоком исходной матрицы. В таком случае возникает возможность рассмотрения исходной матрицы А как некоторой новой (так называемой б л о ч н о й) матрицыi А = Aab, элементами которой служат указанные блоки. Указанные элементы мы обозначаем большой латинской буквой, чтобы подчеркнуть, что они являются, вообще говоря, матрицами, а не числами и (как обычные числовые элементы) снабжаем двумя индексами, первый из которых указывает номер ВлблочнойВ» строки, а второй тАФ номер ВлблочногоВ» столбца.
Например, матрицу
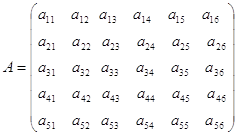
можно рассматривать как блочную матрицу
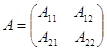
элементами которой служат следующие блоки:
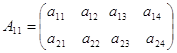
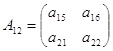
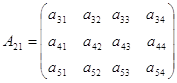
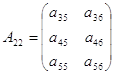
Замечательным является тот факт, что основные операции с блочными матрицами совершаются по тем же правилам, по которым они совершаются с обычными числовыми матрицами, только в роли элементов выступают блоки.
Понятие определителя.
Рассмотрим произвольную квадратВнную матрицу любого порядка п:
A = 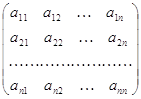(1.7)
С каждой такой матрицей свяжем вполне определенную численВнную характеристику, называемую определителем, соответствующим этой матрице.
Если порядок матрицы (1.7) равен единице, то эта матрица состоит из одного элемен-та аij определителем первого порядка соответствующим такой матрице, мы назовем величину этого элемента.
Если далее порядок п матрицы (1.7) равен двум, т. е. если эта матрица имеет вид
A =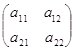 
(1.8)
то определителем второго порядка, соответствующим такой матВнрице, назовем число, равное а11 а22 тАФ а12 а21и обозначаемое одним из символов:
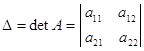
Итак, по определению
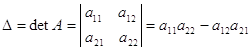(1.9)
Формула (1.9) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Словесная формулировка этого правила такова: определитель второго порядка, соответствующий матрице (1.8), равен разности произведения элементов, стоящих на главной диагонали этой матрицы, и произведения элементов, стоящих на побочной ее диагонали. Определители второго и более высоких порядков находят широкое применение при решении систем линейных уравнений.
Рассмотрим, как выполняются операции с матрицами в системе MathCad. Простейшие операции матричной алгебры реализованы в MathCad в виде операторов. Написание операторов по смыслу максимально приближено к их математическому действию. Каждый оператор выражается соответствующим символом. Рассмотрим матричные и векторные операции MathCad 2001. Векторы являются частным случаем матриц размерности n x 1, поэтому для них справедливы все те операции, что и для матриц, если ограничения осоВнбо не оговорены (например, некоторые операции применимы только к квадратным матрицам n x n). Какие-то действия допустимы только для векторов (например, скалярное произведение), а какие-то, несмотря на одинакоВнвое написание, по-разному действуют на векторы и матрицы.
При работе с матрицами используется панель инструментов тАЬМатрицытАЭ
Рис.1 Панель инструментов Матрицы
Для ввода матрицы:
q введите имя матрицы и знак присваивания (двоеточие)
q щелкните по значку тАЬсоздать матрицутАЭ в панели тАЬМатрицытАЭ.
q
В появившемся диалоге задайте число строк и столбцов матрицы.
q После нажатия кнопки OK открывается поле для ввода элементов матрицы. Для того, чтобы ввести элемент матрицы, установите курсор в отмеченной позиции и введите с клавиатуры число или выражение.
Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно:
q выделить матрицу и щелкнуть в панели по кнопке операции,
q или щелкнуть по кнопке в панели и ввести в помеченной позиции имя матрицы.
Меню тАЬСимволытАЭ содержит три операции - транспонирование, инвертирование, определитель.
Это означает, например, что вычислить определитель матрицы можно, выполнив команду Символы/Матрицы/Определитель.
Номер первой строки (и первого столбца) матрицы MathCAD хранит в переменной ORIGIN. По умолчанию отсчет ведется от нуля. В математической записи чаще принято вести отсчет от 1. Для того, чтобы MathCAD вел отсчет номеров строк и столбцов от 1, нужно задать значение переменной ORIGIN:=1.
Функции, предназначенные для работы с задачами линейной алгебры, собраны в разделе тАЬВекторы и матрицытАЭ диалога тАЬвставить функциютАЭ (напоминаем, что он вызывается кнопкой на панели тАЬСтандартныетАЭ). Основные из этих функций будут описаны позже.
Транспонирование