Инверсия и ее применение

В геометрии основную роль играют различные преобразования фигур. В школе подробно изучаются движения и гомотетии, а также их приложения. Важной особенностью этих преобразований является сохранение ими природы простейших геометрических образов: прямые преобразуются в прямые, а окружности тАУ в окружности. Инверсия представляет собой более сложное преобразование геометрических фигур, при котором прямые уже могут переходить в окружности и наоборот. Такой подход позволяет дать в применении к задачам элементарной геометрии единообразную методику изучения. Это, прежде всего, относится к задачам на построение и к теории пучков окружностей.

Следует отметить, что рассмотрение указанных разделов элементарной геометрии без применения инверсии связано с привлечением разнообразных, большей частью довольно искусственных построений, носящих частный характер.

Кроме указанных приложений, инверсия применяется также в пограничных вопросах элементарной геометрии и так называемой высшей геометрии.

В данной работе и рассматривается преобразование, называемое инверсией. Применение преобразования инверсии при решении задач на построение и доказательство позволяет решить ряд задач, которые трудно решить с помощью других методов решения подобных задач.

Впервые стали изучать это преобразование в 30-х годах прошлого века.

Способ решения задач, который рассматривается в данной работе, называется методом инверсии, или методом обратных радиусов, или методом обращения.

Этот метод является мощнейшим среди методов решения задач на построение, которые могут сыграть серьезную роль в математической подготовке школьника, ведь ни один вид задач не дает, пожалуй, столько материала для развития математической инициативы и логических навыков учащихся как геометрические задачи на построение.

Дана дипломная работа посвящена преобразованию инверсии и ее применению в решении задач на построение. Для удобства изложения материал разбит на две главы.

В первой главе подробно изучается преобразование инверсии: рассматриваются основные свойства инверсии. Во второй главе рассматривается применение инверсии к решению задач на построение, отдельно рассматривается задача Аполлония и вспомогательные задачи, применяемые к решению этой задачи.

В конце второй главы в работе представлено приложение, в котором предложено решение некоторых задач, решаемых с помощью инверсии.

Работа включает в себя также введение, заключение и список используемой литературы.

1. Инверсия как преобразование плоскости

1.1 Определение инверсии. Построение инверсных точек.

Пусть на плоскости дана некоторая окружность щ (О, R) (рис. 1)

Рис. 1

Пусть, далее, Р тАУ произвольная точка плоскости, отличная от точки О. Сопоставим ей точку РТС, которая удовлетворяла бы двум условиям:

1) точка РТС лежит на луче ОР;

2) ОР ОРТС = R2.

Такую точку РТС мы называем инверсной или обратной точке Р относительно окружности щ. Окружность щ называется базисной окружностью инверсии, ее центр тАУ центром инверсии, а радиус тАУ радиусом инверсии.

Преобразование, при котором каждой точке некоторой фигуры ставится в соответствие инверсная ей точка, называется инверсией, а фигура, образованная всеми точками, инверсными точками данной фигуры, называется инверсной по отношению к данной фигуре.

Обратим внимание на то, что при R = 1 ОРТС= 1/ОР, так что ели точка Р инверсна точке РТС, то расстояния ОР и ОРТС являются взаимно обратными числами. С этим связано то, что точку РТС называют обратной точке Р, а рассматриваемое преобразование называется преобразованием обратных радиусов (расстояний), или же обращением.

Рассмотрим построение инверсных точек:

1 случай.

Если точка Р РД (О,Р ), то РТС= Р (совпадают).

2 случай.

Пусть точка Р вне базисной окружности.

Построение.

1. щ (О, R) и Р тАУ данная точка.

2. РК тАУ касательная к окружности щ. К РД щ.

3. КРТС┴ОР, РТС РД ОР, РТС - инверсна точке Р. (рис 2).

Рис. 2.

Доказательство.

Рассмотрим подобные треугольники ОРК и ОКРТС. Из подобия следует: 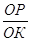= 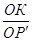или ОР ОРТС = R2 .

Точка РТС РД ОР (по построению).

3 случай.

Точка Р тАУ внутри базисной окружности. Тогда построение выполняем в обратом порядке.

Построение.

1. щ (О, R) и Р тАУ данная точка.

2. РК┴ОР, К РД щ.

3. КР тАУ касательная к окружности.

1.2 Свойства инверсии

Прежде, чем рассмотреть свойства инверсии, установим одну простую лемму, которая играет существенную роль при изучении свойств инверсии.

Лемма. Пусть инверсия ц переводит точки А и В соответственно в точки АТС и ВТС (предполагается, что точки А и В отличны от точки О и бесконечно удаленной точки и, кроме того, точки О, А, В не лежат на одном луче с началом в точке О). Тогда треугольники ОАВ и ОАТСВТС подобны и ∟ОАВ= ∟ОВТСАТС, ∟ОВА= ∟ОАТСВТС.

Доказательство: У треугольников ОАВ и ОАТСВТС (рис.3) имеется общий угол, а стороны, заключающие этот угол, пропорциональны. Действительно, так как ОАОАТС = ОВОВТС = r2, то = 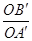. Отсюда следует, что треугольники ОАВ и ОАТСВТС подобны.

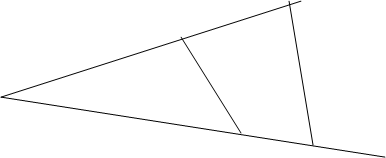
Рис 3.

Но так как против пропорциональных сторон в подобных тре6угольниках лежат равные углы, то из соотношения = 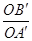следует равенство соответствующих углов: ∟ОАВ= ∟ОВТСАТС, ∟ОВА= ∟ОАТСВТС.

Лемма доказана.

Теорема 1. Инверсия ц переводит любую прямую, проходящую через центр инверсии, саму на себя, т. е. прямая, проходящая через центр инверсии, есть инвариантная фигура.

Доказательство этой теоремы непосредственно вытекает из определения инверсии.

Теорема 2. Инверсия ц преобразует прямую, не проходящую через центр инверсии О, в окружность, проходящую через точку О.

Доказательство: Пусть l тАУ прямая, не проходящая через центр инверсии тАУ точку О. Опустим из точки О перпендикуляр на прямую l , и пусть он пересекает l в точке М (рис 4). Пусть МТС образ точки М относительно инверсии ц. Точка МТС, очевидно, лежит на луче ОМ. На прямой l рассмотрим произвольную точку X, отличную от бесконечно удаленной точки О ∞. Пусть XТС - образ Х относительно инверсии ц. Тогда по лемме 1 имеем ∟ОXТСМТС = ∟ОМХ = 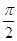. Поэтому точка XТС лежит на окружности К, построенной на отрезке ОМТС как на диаметре. Так как точка Х взята на прямой l произвольно, то образ прямой l при инверсии ц представляет собой совокупность точек l′, расположенную на окружности К.

Рис. 4

Докажем теперь, что множество точек l′ совпадает с окружностью К. прежде всего отметим, что точка О принадлежит множеству l′. Это вытекает из того, что прямая l проходит через бесконечно удаленную точку О ∞, а эту точку инверсия ц переводит в точку О. Пусть теперь Y тАУ произвольная точка окружности К. Луч ОY пересекает прямую l в некоторой точке Z. Так как точки Y и Z лежат на одном луче ОZ, то нам нужно лишь проверить, что выполняется соотношение ОY = 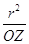. По построению треугольники ОYМТС и ОМZ (рис 4) подобны. Поэтому 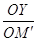= 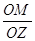. Отсюда ОY = 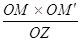= 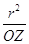. Итак, доказано, что точка Y есть образ точки Z при инверсии ц.

Теорема доказана.

Построение, проведенное в доказательстве теоремы 2, дает способ построения образа заданной прямой относительно инверсии ц с помощью циркуля и линейки. Из центра инверсии тАУ точки О тАУ опускаем перпендикуляр ОМ (рис 4) на прямую l. Строим точку МТС, являющуюся образом точки М (при этом приходится строить отрезок длиной, равной r2/ОМ). Образ прямой l относительно инверсии тАУ окружность lТС - строится на отрезке ОМТС как на диаметре.

Теорема 3. Инверсия ц преобразует окружность, проходящую через центр инверсии О, в прямую, не проходящую через точку О.

Доказательство этой теоремы вытекает из доказательства теоремы 2.

Теорема 4. Инверсия ц преобразует окружность, не проходящую через центр инверсии О, в некоторую окружность, также не проходящую через центр инверсии.

Доказательство: пусть К тАУ окружность, не проходящая через центр инверсии О. Через точку О проведем прямую g так, чтобы она пересекала окружность К по диаметру АВ (рис 5).

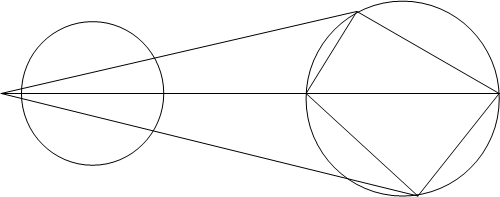
Рис 5.

Пусть АТС и ВТС - образы точек А и В относительно инверсии ц, Х тАУ произвольная точка окружности К и ХТС - ее образ.

По лемме 1 треугольники ОХА и ОХТСАТС подобны и потому ∟ОАТСХТС = ∟ОХА; аналогично треугольники ОХВ и ОХТСВТС подобны и, следовательно, ∟ОВТСХТС = ∟ОХВ.

Так как ∟АТСХТСВТС = ∟ОВТСХТС - ∟ОАТСХТС = ∟ОХВ - ∟ОХА = ∟АХВ = 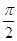, то отсюда вытекает, что отрезок АТСВТС из точки ХТС виден под углом 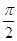и, стало быть, точка ХТС лежит на окружности S, построенной на отрезке АТСВТС как на диаметре. Поскольку точка Х на окружности К была выбрана произвольно, то КТС - образ окружности К при инверсии ц тАУ расположен на окружности S. Пусть Y тАУ произвольная точка окружности S и Z тАУ точка на луче ОY такая, что ОZ = 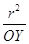. Очевидно, что точка Z переводится инверсией ц в точку Y. Далее, из соотношений

ОА ОАТС = r2

ОВ ОВТС = r2

ОZ OY = r2

и леммы 1 вытекает, что ∟AZB = ∟OZB - ∟OZA = ∟OB′Y - ∟OA′Y =∟A′YB′ = .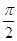

Следовательно, что точка Z лежит на окружности К. отсюда вытекает, что фигуры S и КТС совпадают. Так как по построению концы диаметра окружности К тАУ точки А, В тАУ отличны от точки О, то окружность КТС не проходит через точку О.

Построения , приведенные выше, дают возможность строить образ окружностей при инверсии с помощью циркуля и линейки. Рассмотрим этот вопрос более подробно.

а) Окружность не проходит через центр инверсии. В этом случае проводим из точки О луч, который пересекает окружность К по диаметру АВ, для точек А и В строим их образы АТС и ВТС. окружность КТС - образ окружности К относительно инверсии ц тАУ есть окружность, построенная на отрезке АТСВТС как на диаметре (рис. 6).

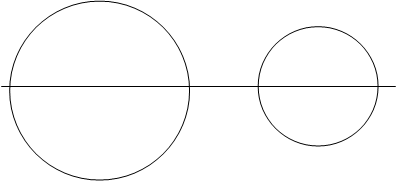
Рис. 6

б) Окружность К проходит через центр инверсии. В этом случае согласно теореме 3 образ К есть прямая КТС. из точки О проводим луч ОА (рис 7), который пересекает К по диаметру ОА. Для точки А строим ее образ тАУ точку АТС. Прямая, проходящая через точку АТС перпендикулярно лучу ОА, и есть искомая прямая КТС

Построение прямой КТС значительно упрощается в двух случаях:

1) если окружность К пересекает окружность инверсии в двух точках В и С, то прямая КТС совпадает с прямой ВС (рис. 8);

2) если К касается окружности инверсии, то КТС есть касательная к окружности инверсии в точке касания К с окружностью инверсии (рис. 9).

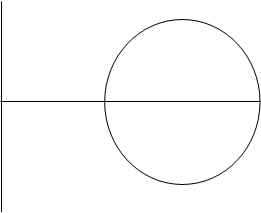
Рис. 7

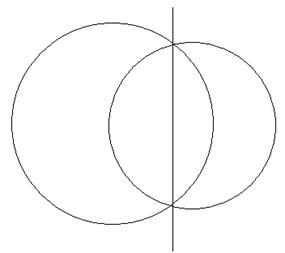
Рис. 8

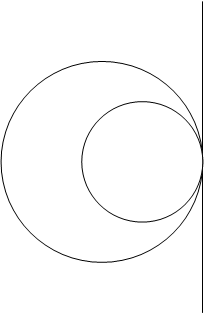
Рис. 9

Рассмотрим теперь вопрос о характере изменения углов между кривыми под действием инверсии ц. Как известно, углом между кривыми L1 и L2 в точке их пересечения называется наименьший из вертикальных углов между касательными к этим кривым в рассматриваемой точке. Можно доказать, что при инверсии углы между кривыми сохраняются. Ниже это предложение доказывается для окружностей и прямых.

Теорема 5. При инверсии ц угол между прямыми равен углу между их образами.

Доказательство. Здесь могут представиться 3 случая:

1) прямые l1 и l2 проходят через центр инверсии ц;

2) одна из прямых l1 и l2 проходит через центр инверсии;

3) ни l1 и l2 не проходят через центр инверсии.

В первом случае утверждение теоремы очевидно. Рассмотрим случаи 2) и 3). В случае 2) (рис. 10) будем считать для определенности, что прямая l1 проходит через центр инверсии - точку О. Тогда инверсия ц переводит прямую l1 саму в себя, т.е. образ прямой l1 совпадает с этой прямой. Прямая l2 не проходит через центр инверсии и потому переводится инверсией в некоторую окружность lТС2, проходящую через точку О. Касательная t к окружности lТС2 в точке О параллельно прямой l2.

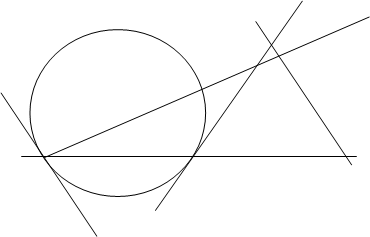
Рис. 10

Относительно взаимного расположения прямых l1 и l2 могут представиться 2 возможности:

а) прямые l1 и l2 параллельны;

б) l1 и l2 пересекаются в некоторой точке А.

Если l1 и l2 параллельны, то угол между ними, очевидно, равен 0. Но прямая l1 проходит через точку О и параллельна l2 . Поэтому она необходимо будет совпадать с касательной t к окружности lТС2 в точке О. Отсюда следует, что угол между lТС1 и lТС2 равен 0 и, следовательно, утверждение теоремы в случае а) доказана.

Пусть теперь l1 и l2 не параллельны и А тАУ точка их пересечения. Обозначим через б наименьший из вертикальных углов между l1 = lТС1 и прямой l2 или, что то же, прямой t. Точка А при инверсии переходит в некоторую точку АТС, в которой прямая lТС1 пересекается с окружностью lТС2. Но прямая lТС1 или, что то же, прямая ОАТС составляет с касательной tТС в точке АТС к окружности lТС2 такие же вертикальные углы, что и с касательной t. Отсюда немедленно следует, что угол между l1 и l2 в точке АТС равен б. случай 2) полностью доказан.

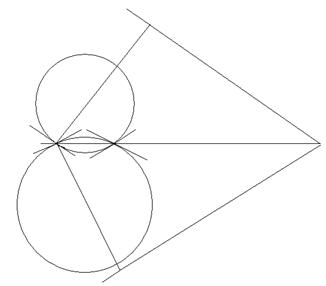
Рис. 11

Третий случай (рис. 11) доказывается аналогичными рассуждениями. Заметим только, что если прямые l1 и l2 параллельны, то соответствующие окружности lТС1 и lТС2 имеют в точке О общую касательную и составляют между собой нулевой угол. Отсюда угол между lТС1 и lТС2 равен углу между l1 и l2. Если же прямые l1 и l2 пересекаются, то, как видно из рис. 11, угол между окружностями lТС1 и lТС2 в точке О равен углу между прямыми l1 и l2, т. к. касательные t1 и t2 к этим окружностям в точке О параллельны прямым l1 и l2. Отсюда и вытекает утверждение теоремы.

Рассмотрим еще две теоремы без доказательства.

Теорема 6. Угол между окружностями равен углу между образами этих окружностей относительно инверсии.

Теорема 7. Угол между окружностью и прямой равен углу между образами этих фигур относительно инверсии.

1.3 Лемма об антипараллельных прямых

Сначала рассмотрим вспомогательное понятие.

Пусть некоторая прямая a пересекает обе стороны некоторого угла (k, l) (рис. 12). В пересечении с какойтАУлибо из сторон угла, например k, эта прямая образует четыре угла, из которых только один лежит внутри треугольника, отсекаемого прямой от угла (k, l).

Рис. 12

В дальнейшем, когда речь будет идти об угле между прямой и стороной угла, мы будем иметь в виду именно этот угол.

Пусть теперь две прямые (рис. 13) пересекают стороны угла, причем одна из них образует с одной из сторон угла такой же угол, какой вторая прямая образует с другой стороной угла (на рис. 13) ∟1 = ∟2.

Рис. 13

Легко понять, что когда и первая прямая образует со второй стороной угла такой же угол, какой образует вторая прямая с первой стороной угла ∟3 = ∟4.

Определение. Две прямые, пересекающие стороны некоторого угла, называются антипараллельными относительно этого угла, если одна из них образует с одной из его сторон такой же угол, какой образует другая прямая с другой его стороной.

Антипараллельными являются прямые a и b на рисунке 13, прямые с и d на рисунке 14, где с ┴ k и d ┴ l.

Антипараллельные прямые, вообще говоря, не параллельны. Исключение составляет только случай, когда обе прямые перпендикулярны к биссектрисе данного угла (рис. 15).

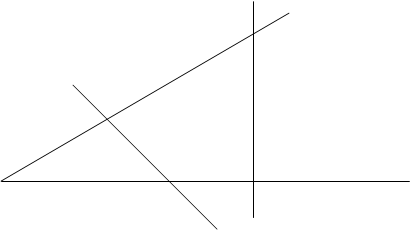
Рис. 14

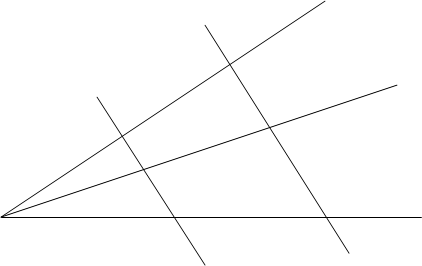
Рис. 15

Теорема (лемма об антипараллельных прямых). Прямая, соединяющая две точки плоскости, и прямая, соединяющая две инверсные им точки, антипараллельны относительно угла с вершиной в центре инверсии и сторонами, проходящими через данные точки.

Доказательство. Пусть щ (О, R) базисная окружность, точки АТС и ВТС (рис. 16) инверсны соответственно точкам А и В. Тогда ОА ОАТС = ОВ ОВТС = R2, так что 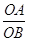= 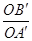. Кроме того, в треугольниках АОВ и ВТСОАТС угол О общий. Следовательно, ∆АОВ подобен ∆ ВТСОАТС и, значит, ∟ОВА = ∟ОА′В′.

Таким образом, прямые АВ и А′В′ антипараллельны относительно угла АОВ, что и требовалось доказать.

Если (рис. 16) каким-либо образом построены две соответственные в инверсии точки А и А′, то доказанная лемма дает простой прием построения образа произвольной точки В (не лежащей на прямой ОА): соединить В с А и провести прямую А′В′ так, чтобы ∟ОА′В′ = ∟ОВА.

Рис. 16

1.4 Степень точки относительно окружности

Понятие степени точки относительно окружности играет существенную роль и является аналогом понятия расстояния от точки до прямой.

Степенью точки М относительно окружности К называется число

s = d2 тАУ r2 ,

где d тАУ расстояние точки М от центра О окружности К, а r тАУ радиус этой окружности. Если точка М лежит внутри окружности К, то d < r, и потому степень точки М: s = d2 тАУ r2 тАУ отрицательна. Величины r тАУ d и r + d суть отрезки диаметра PQ, на которые его разбивает точка М. Поэтому для любой хорды АМВ круга К (рис. 17) имеем s = - АМ МВ.

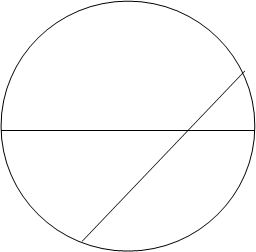
Рис. 17

Если точка М лежит на окружности К, то d = r и, следовательно, степень точки М равна нулю. Наконец, если точка М лежит вне окружности К, то d > r и s = d2 тАУ r2 представляет собой квадрат длины касательной к окружности К, проведенной из точки М (рис. 18).

Рис. 18

Пусть теперь даны две окружности К1 и К2. Геометрическое место точек, степени которых относительно окружностей К1 и К2 равны, называют радикальной осью окружностей К1 и К2.

1.5 Инверсия окружностей, проходящих и не проходящих через центр инверсии

Путь некоторая окружность г проходит через центр инверсии тАУ точку О. При инверсии все точки окружности г, за исключением точки О, преобразуются в какие-то другие точки. Какую фигуру образуют эти точки?

Теорема. При инверсии окружность, проходящая через центр инверсии, преобразуется в прямую. Эта прямая перпендикулярна к линии центров данной окружности и базисной окружности.

Доказательство. Пусть щ (О, R) тАУ базисная окружность инверсии, г (О1, R1) тАУ данная окружность, проходящая через О. Проведем прямую О О1. Пусть она пересечет окружность г в точке А (рис. 19).

Рис. 19

Обозначим через АТС точку, инверсную точке А. Выберем на окружности г произвольную точку Р и построим ей инверсную точку РТС. соединим Р с А, РТС с АТС. В силу леммы об антипараллельных прямых ∟ОАТСРТС = ∟ОРА. Но ∟ОРА = 90˚, как опирающийся на диаметр окружности г. Поэтому ∟ОАТСРТС тоже равен 90˚, т. е. точка Р′ лежит на прямой, проходящей через точку А′ и перпендикулярной к прямой ОА′. Обозначим прямую Р′А′ через а. Мы показали, что каждая точка окружности г преобразуется в точку прямой а. Не трудно показать, что и обратно: каждая точка прямой а инверсна некоторой точке окружности г. Следовательно, окружность г преобразуется при инверсии в прямую а, что и требовалось доказать.

Из рассмотренной теоремы вытекает способ построения прямой, инверсной данной окружности, если последняя проходит через центр инверсии: 1) строим прямую ОО1, проходящую через центр инверсии и центр данной окружности; 2) отмечаем точку А пересечения этой прямой с данной окружностью (А ≠ О); 3) строим точку А′, инверсную точке А, и 4) через точку А′ проводим прямую а, перпендикулярную прямой ОО1. Полученная прямая а искомая.

В том случае, когда базисная окружность пересекает данную окружность г, построение упрощается: прямой, инверсной окружности г, является прямая, определяемая двумя точками пересечения окружности г с базисной окружностью (рис. 20).

Если окружность г касается базисной окружности щ, то г преобразуется в общую касательную этих окружностей.

Если две окружности касаются в центре инверсии, то они преобразуются при инверсии в пару параллельных прямых.

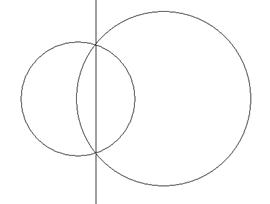
Рис. 20

Теорема. При инверсии окружность, не проходящая через центр инверсии, преобразуется в окружность.

Доказательство. Пусть щ (О, r) тАУ базисная окружность (рис. 21), г (О1, r1) тАУ данная окружность. Проведем прямую ОО1 и отметим точки А и В ее пересечения с окружностью г. Пусть АТС и ВТС - инверсные им точки. Обозначим через Р произвольную точку окружности г, через РТС - инверсную ей точку. Соединим Р с А и В, РТС с АТС и ВТС. из леммы об антипараллельных прямых вытекает, что ∟1′ = ∟1, ∟2′ = ∟2. Но ∟1 + ∟2 = 90i. Поэтому ∟1ТС + ∟2ТС = 90i. Следовательно, ∟АТСРТСВТС = 90i. Таким образом, из точки РТС отрезок АТСВТС виден под прямым углом. Значит, точка РТС лежит на окружности с диаметром АТСВТС. Обозначим эту окружность через гТС. Мы доказали, что каждая точка окружности г при инверсии преобразуется в точку окружности гТС.

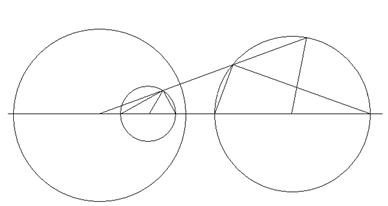
Рис. 21

По ходу доказательства теоремы выясняется следующий способ построения окружности, инверсной данной окружности (если последняя не проходит через центр инверсии): 1) проводим прямую через центр инверсии О и центр О1 данной окружности г; 2) отмечаем точки А и В пересечения этой прямой с окружностью гТС; 3) строим инверсные точки АТС и ВТС; 4) строим окружность гТС на отрезке АТСВТС как на диаметре. Окружность гТС искомая.

1.6 Преобразование прямой при инверсии

При инверсии прямая, проходящая через центр инверсии, преобразуется сама в себя. Как обстоит дело с прямой, не проходящей через центр инверсии?

Теорема. При инверсии прямая, не проходящая через центр инверсии, преобразуется в окружность, проходящую через центр инверсии.

Доказательство. Пусть щ (О, r) тАУ базисная окружность (рис. 22), а тАУ данная прямая. Опустим из точки О перпендикуляр ОА на прямую а. Пусть АТС - точка, инверсная точке А, а г тАУ окружность, имеющая диаметром ОАТС.

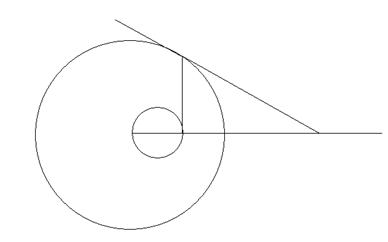
Рис. 22

При инверсии окружность г преобразуется в прямую а (по теореме из пункта 1.5). в силу свойства взаимности прямая а преобразуется в окружность г.

Заметим, что по ходу доказательства мы выяснили способ построения окружности, инверсной данной прямой.

1.7 Инвариантные окружности. Сохранение углов при инверсии

При инверсии базисная окружность преобразуется в себя. Но существуют и другие окружности, обладающие таким свойством.

Вспомним некоторые определения.

Углом между двумя линиями в точке их пересечения Т называется угол между касательными к этим линиям, проведенным в точке Т.

Две окружности называются ортогональными, если они пересекаются под прямым углом. Если две окружности ортогональны, то их радиусы, проведенные в точку пересечения, перпендикулярны между собой, и наоборот.

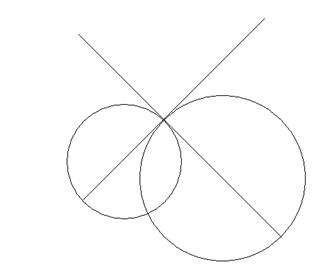
Рис. 23

Отсюда вытекает способ построения окружностей, ортогональных данной окружности щ в данной точке Т. для этого достаточно на касательной t к окружности щ в точке Т выбрать произвольную точку О1 и построить окружность щ1 (О1, О1Т), которая и будет искомой (рис. 23).

Теорема. Для того чтобы окружность, отличная от базисной окружности, преобразовалась при инверсии в себя, необходимо и достаточно, чтобы она была ортогональна базисной окружности.

Доказательство. 1) Достаточность. Пусть окружность г (О1, r1) (рис. 24) ортогональна базисной окружности щ (О, r). Докажем, что окружность г преобразуется в себя.

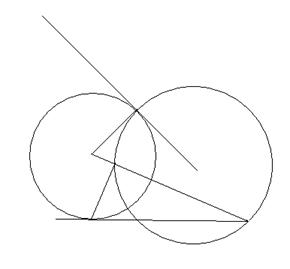
Рис. 24

Пусть Р тАУ произвольная точка окружности г. Проведем прямую ОР. Она пересечет окружность г еще в некоторой точке Р1 (если прямая ОР касается окружности г, то за Р1 примем точку Р).

Так как окружность г ортогональна окружности щ, то радиус ОТ, соединяющий центр инверсии с точкой пересечения окружностей, касается окружности г. Поэтому ОР ОР1 = ОТ2 = r2, так что точка Р1 инверсна точке Р. Итак, при инверсии относительно окружности щ каждая точка Р окружности г преобразуется в точку Р1, также лежащую на окружности г.

Принимая во внимание свойство взаимности инверсных точек, можно заключить также, что и обратно: каждая точка окружности г служит образом некоторой точки этой же окружности. Таким образом, окружность г преобразуется в себя.

2) Необходимость. Пусть окружность г, отличная от базисной окружности инверсии, преобразуется в себя. Докажем, что г тАУ окружность, ортогональная базисной. Так как окружность г отлична от окружности щ, то она содержит точку Р, не лежащую на щ. Пусть точка Р1 инверсна точке Р (рис. 24); тогда одна из двух точек Р и Р1 находится вне, а другая внутри окружности щ. Следовательно, окружность г пересекает окружность щ. Обозначим через Т одну из точек их пересечения. Покажем, что ОТ тАУ касательная к окружности г. Это можно установить способом Влот противногоВ». Допустим, что, помимо точки Т, прямая ОТ встречает окружность г еще в точке Т1. Заметим, что точки Р и Р1 расположены по одну сторону от точки О, так что точка О расположена вне окружности г. В силу известного свойства секущих, проведенных из одной и той же точки к окружности, ОТ ОТ1 = ОР ОР1 = r2. И так как ОТ = r, то и ОТ1 = r. Следовательно, точка Т1 должна совпасть с точкой Т, вопреки допущению. Итак, ОТ тАУ касательная к окружности г. Следовательно, окружности щ и г ортогональны.

Теорема. Если окружность проходит через две взаимно инверсные точки, то при инверсии она преобразуется в себя.

Доказательство. Пусть окружность г проходит через точки Р и РТС, инверсные относительно окружности щ (О, r). Тогда ОР ОРТС = r2. Ясно, что точка О вне окружности г. Пусть Q тАУ произвольная точка на окружности г (рис. 25).

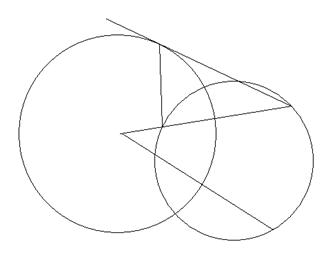
Рис.25

Проведем луч ОQ, и пусть он встречает окружность г в точках Q и QТС (в случае касания луча ОQ с окружностью г QТС≡ Q), тогда ОQ OQТС = OP OPТС = r2, т. е. точка QТС инверсна точке Q. Итак, если какая-либо точка лежит на окружности г, то инверсная ей точка также лежит на этой окружности. Отсюда заключаем, что при инверсии окружность г преобразуется в себя.

Следствие. Окружность, проходящая через две взаимно инверсные точки, ортогональна к базисной окружности инверсии. Все окружности, проходящие через две взаимно инверсные точки, образуют эллиптический пучок, состоящий из окружностей, ортогональных базисной окружности инверсии.

Пусть через точку М проходят две линии г1 и г2. предположим, что существует единственная касательная к каждой из этих линий в точке М. пусть при инверсии точка м преобразуется в точку М′, а линии г1 и г2 соответственно в линии г1′ и г2′. Оказывается, что угол между линиями г1′ и г2′ в точке М′ равен углу между линиями г1 и г2 в точке М.

Лемма. Если при инверсии относительно окружности щ (О, r) точка М и проходящая через нее линия г преобразуется в точку М′ и линию г′, то линии г и г′ в этих точках образуют с прямой ОМ равные углы.

Рис. 26

Доказательство. Пусть Р (рис. 26) тАУ произвольная точка на линии г, Р′ - ей инверсная точка; тогда Р′ лежит на г′.

Соединим М с Р, М′ с Р′. В силу леммы об антипараллельных прямых ∟ММ′Р′ = ∟МРО или ∟ММ′Р′ = ∟М′МР - ∟МОРтАж (1).

Пусть при неограниченном приближении точки Р вдоль линии г к точке М секущая МР стремится к положению МА, так что МА - касательная к линии г в точке М. Пусть ∟М′МА = ц. Тогда

lim ∟М′МР = ц.

P → M

В то же время, когда Р стремится к М вдоль линии г, угол МОР стремится к нулю. Поэтому, в силу равенства (1), угол ММ′Р′ также стремится к определенному пределу, равному ц. Таким образом, когда Р стремится к М вдоль линии г (и, следовательно, Р′ стремится к М′ на линии г′), секущая М′Р′ стремится к некоторому предельному положению М′А′. А′М′ - касательная к г′ в точке М′ (по определению касательной). Мы видим, что ∟ММ′А′ = ц. Лемма доказана.

Теорема. Если две линии г1 и г2 и точка их пересечения М преобразуются в некоторой инверсии соответственно в линии г1′ и г2′ и точку М′, то угол между линиями г1 и г2 в точке М равен углу между линиями г1′ и г2′ в точке М′.

Рис. 27

Доказательство. Пусть а1 и а2 тАУ касательные к г1 и г2 в точке М, а1′ и а2′ - касательные к г′1 и г′2 в точке М′ (рис. 27).

Будем предполагать, что ни одна из прямых а1 и а2 не совпадают с прямой ОМ, где О тАУ центр инверсии; в противном случае доказательство только упрощается. Прямой ММ′ плоскость разбивается на две полуплоскости. Выберем в одной из них на каждой прямой а1, а2 и а′1, а′2 по одной точке: А1 и А2; А1′ и А2′. В силу леммы

∟М′МА1 = ∟ ММ′А1′ (2)

∟М′МА2 = ∟ ММ′А2′ (2′).

Пусть для определенности ∟М′МА2 < ∟М′МА1, отсюда ∟А2МА1 = ∟М′МА1 - ∟М′МА2 и ∟ А2′М′А1′ = ∟ ММ′А1′ - ∟ ММ′А2′ , так что в силу равенств (2) и (2′) ∟А1′М′А2′ = ∟А1МА2. Теорема доказана.

Следствие. Если две линии касаются в некоторой точке, отличной от центра инверсии, то при инверсии они преобразуются в две линии, которые касаются в соответственной точке.

1.8 Инверсия и осевая симметрия.

Можно установить далеко идущую аналогию в свойствах инверсии и осевой симметрии. Для этого напомним некоторые свойства инверсии.

1. Инверсия сохраняет угол пресечения двух линий, меняя при этом его ориентацию.

2. Прямая, ортогональная базисной окружности, преобразуется в себя.

3. Базисная окружность преобразуется в себя.

4. Всякая окружность, ортогональная базисной, преобразуется в себя.

5. Всякая окружность или прямая преобразуется в окружность или прямую.

6. Две точки тогда и только тогда инверсны относительно некоторой базисной окружности, если они являются вершинами пучка окружностей, ортогональных к базисной.

Если в этих предложениях слово ВлинверсияВ» заменить словами Влосевая симметрияВ», выражение Влбазисная окружностьВ» - через Влось симметрииВ» и Влинверсные точкиВ» - через Влсимметричные точкиВ», то получим свойства осевой симметрии.

Покажем, что в известном смысле осевую симметрию можно рассматривать как предельный случай инверсии. Пусть базисная окружность инверсии щ (О, r) проходит через точку А (рис. 28), так что ОА = r. Обозначим через а касательную к окружности щ в точке А.

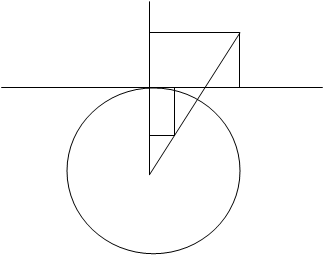
Рис. 28

Пусть, деле, Р тАУ некоторая данная точка, РТС - инверсная ей точка относительно окружности щ. Представим себе, что центр инверсии неограниченно удаляется от точки А вдоль луча Ао, так что радиус инверсии ОА неограниченно возрастает.

В известном смысле можно говорить, что при этом окружность щ (О, r) неограниченно приближается к прямой а, ВлвырождаетсяВ» в эту прямую. Оказывается, что при этом точка РТС будет перемещаться по плоскости, неограниченно приближаясь к точке Р1, симметричной с точкой Р относительно прямой А. Докажем это.

Для определенности положим, что точка Р и точка О лежат по разные стороны от прямой а (рис. 28). Опустим из точки Р перпендикуляр РN на прямую а и перпендикуляр РL на прямую ОА. Пусть РN = р, РL = m. Из точки РТС, инверсной точке Р относительно окружности щ (О, r), также опустим перпендикуляры РТСF и РТСК на прямые а и ОА. Нам нужно показать, что РТСF→ р и РТСК→ m, если r → ∞. Действительно,

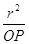
РТСF = КА = r - ОРТС Cosб = r тАУ Cosб = r тАУ =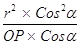

= r - 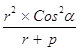= 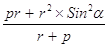. Но

tgб = 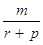, и поэтому

Sin2б = = = = .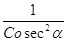

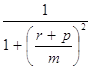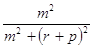Следовательно, PТСF = = .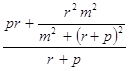

Отсюда видно, что РТСF → р, когда r → ∞. С другой стороны, РТСК = = ОРТС Sinб = = = .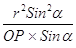

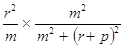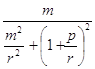Отсюда ясно, что РТСК→ m, когда r→ ∞.

Изложенные здесь изображения показывают, что целесообразно расширить понятие об инверсии так, чтобы можно было рассматривать осевую симметрию как специальный случай инверсии. Для этого условимся называть Влокружностью в широком смысле словаВ» любую окружность и любую прямую. Тогда можно оба преобразования тАУ инверсию и симметрию относительно прямой тАУ объединить в одно понятие с помощью следующего определения. Точка РТС называется обратной точке Р (или сопряженной точке Р) относительно окружности (в широком смысле) щ, если точки Р и РТС являются вершинами пучка окружностей ортогональных к щ. Такое преобразование, при котором каждой точке Р сопоставляется сопряженная ей точка РТС относительно окружности (в широком смысле) щ, назовем отражением от окружности щ. В том случае, когда щ является окружностью в узком (обычном) смысле, наше преобразование представляет инверсию относительно щ. Если же щ тАУ прямая, то рассматриваемое преобразование является симметрией относительно этой прямой.

1.9 Инверсор

Существуют приборы с помощью которых можно без всяких вычислений и без привлечения обычных инструментов геометрических построений вычертить линию, инверсную любой данной линии.

Впервые инверсор был предложен французским капитаном Поселье в 1864 году. Этот прибор получил известность только через семь лет, когда он был зависимо от Поселье изобретен петербургским студентом Липкиным, видимо, под влиянием идей П. Л. Чебышева.

ВлКлетка ПосельеВ», как принято называть этот инверсор, состоит из шести стержней, связанных шарнирами (рис. 29). Четыре из них составляют ромб PAQB. Остальные два стержня равны между собой, но каждый из них длиннее стороны ромба PAQB.

Обозначим РА через а, ОА через l, а разность l2 тАУ a2 через R2. Предположим, что точка О закреплена на плоскости. Тогда при любом положении точки Р на плоскости точка Q будет ей инверсна относительно окружности щ (О, R). В самом деле: 1) Р и Q лежат на одном луче, исходящем из точки О, и 2) ОР ОQ = (ОС - РС) (ОС + РС) = ОС2 тАУ РС2 = (l2 тАУ АС2) тАУ (а2 тАУ АС2) = l2 тАУ а2 = R2.

Рис. 29

Когда точка описывает какую-нибудь линию г, точка Q описывает инверсную ей линию гТС. В частности, когда Р описывает окружность, проходящую через точку О, точка Q опишет прямую. Таким образом, инверсор Поселье позволяет преобразовать вращательное движение в прямолинейное. Если нужно преобразовать в инверсии окружность радиуса r, то к инверсору в точке Р шарнирно присоединяется стержень МР длины r. Если точки О и М закреплены неподвижно так, что стержни ОА и ОВ могут вращаться около точки О, а стержень МР - около точки М (рис. 30), то точка Р опишет дугу некоторой окружности, а точка Q тАУ дугу инверсной ей окружности или прямолинейный отрезок (в случае, если ОМ = МР).

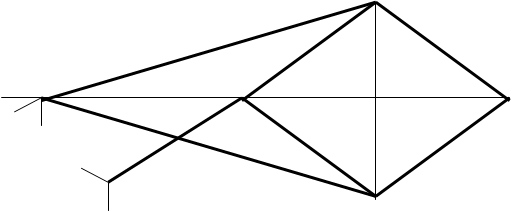
Рис. 30

Инверсор Гарта. Пусть четыре стержня связаны шарнирно так, как указано на рисунке 31. узлы А, В, С и D являются здесь вершинами равнобочной трапеции, причем АВ = СD = d, АD = СВ = l. Пусть О, Р, и Q три точки на этих стержнях, причем = = 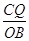. В таком случае точки О, Р и Q лежат на одной прямой, параллельной основанию трапеции АСDВ. Предположим, что точка О закреплена на плоскости, а четыре стержня как-то расположены на этой плоскости. Оказывается, что при любом расположении механизма произведение ОР ОQ постоянно.

Рис. 31

Покаже

Вместе с этим смотрят:

10 способов решения квадратных уравнений

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнженерна графiка

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй