Организация процесса повторения в курсе геометрии 7-9 классов
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра математического анализа и МПМ
Выпускная квалификационная работа
Организация процесса повторения в курсе геометрии 7-9 классов
Выполнила:
студентка V курса математического факультета
Шестакова Ирина Валерьевна
Научный руководитель:
кандидат педагогических наук, доцент кафедры математического анализа и МПМ И.В. Ситникова
Рецензент:
кандидат педагогических наук З.В. Шилова
Допущена к защите в государственной аттестационной комиссии
Вл___В» __________2005 г. Зав. кафедрой М.В. Крутихина
Вл___В»___________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение. 3
Вз1 Требования к организации повторения. 6
Вз2 Виды повторения. 10
2.1. Повторение пройденного в начале года. 10
2.2. Текущее повторение ранее пройденного. 12
2.3. Тематическое повторение. 15
2.4. Заключительное повторение. 19
2.5. Классификация повторения в зависимости от содержания повторяемого материала 24
Вз3 Подготовка учителя к урокам повторения. 28
Вз4 Методы, формы и средства повторения. 34
Заключение. 53
Библиографический список. 54
Приложение. 56
ВведениеВ процессе обучения математике повторению изученного материала отводится важное место. Правильно организованное повторение тАУ один из факторов, способствующих интеллектуальному развитию каждого школьника, достижению им глубоких и прочных знаний. Без сохранения приобретенных знаний, без умения применить пройденный материал в необходимый момент - изучение нового материала всегда сопряжено с большими трудностями и не дает надлежащего эффекта. Таким образом, цель повторения тАУ установить логические связи между вновь изучаемым и ранее изученным материалом, обогатить память, расширить кругозор, привести знания в систему, самоорганизовать ученика.
Необходимость повторения обусловлена задачами обучения, требующими прочного и сознательного овладения им.
Указывая на важность процесса повторения учебного материала, современные исследователи показали значительную роль при этом таких дидактических приемов, как сравнение, классификация, анализ, синтез, обобщение, содействующих интенсивному протеканию процесса запоминания. При этом вырабатываются гибкость, подвижность ума, обобщенность знаний.
В процессе повторения память у учащихся развивается. Эмоциональная память, опирающаяся на наглядно-образные процессы, постепенно уступает памяти с логическими процессами мышления, которая основана на умении устанавливать связи между известными и неизвестными компонентами, сопоставлять абстрактный материал, классифицировать его, обосновывать свои высказывания.
Повторение учебного материала по математике осуществляется во время всего учебного процесса: при изложении учителем новых понятий, при закреплении изученного ранее, при организации самостоятельных работ различных видов, при проверке знаний учащихся и т. д.
Необходимость повторения изученного ранее материала вызвана самой структурой программы учебного курса математики. Изучение некоторых вопросов школьного курса математики осуществляется постепенно, а развитие ее основных идей продолжается на протяжении всего периода обучения в школе, и вследствие этого учащиеся в подавляющем большинстве своем недостаточно видят эти идеи, являющиеся остовом, на котором закрепляются все другие вопросы курса. Поэтому возникает необходимость работы над ведущими идеями, что успешно осуществляется при повторении.
В процессе изучения геометрии повторение имеет особое значение. Специфика предмета повторения состоит в том, что материал каждого урока логически связан с ранее пройденным, иногда далеко отстоящим по времени от изучаемого. Ученик лишь в том случае станет активным участником учебного процесса, если при получении новых знаний у него будет иметься соответствующая база знаний. Ее наличие во многом определяется систематическим и правильно организованным повторением.
Однако повторению в курсе геометрии 7-9 класс уделяется мало внимания.
В связи с этим особо важное значение для организации успешного обучения учащихся геометрии имеет систематическое повторение ранее изученного, связанного с данным уроком, с материалом предшествующих лет, т. е. систематическое возвращение к ранее изученному.
Таким образом, актуальность темы работы обусловлена:
- необходимостью развития творческого мышления учащихся и обучения основным методам научного познания: обобщению, конкретизации, аналогии и т. д.;
- отсутствием достаточно-разработанной методики организации повторения в курсе геометрии 7-9 класс;
- недостаточным умением учащихся самостоятельно систематизировать знания, полученные в разное время, пользоваться ими при необходимости;
- недооценкой роли повторения в процессе обучения.
Объект исследования: процесс изучения геометрии в 7-9 классах.
Предмет исследования: организация повторения при изучении геометрии в 7-9 классах.
Цель работы: изучить цели и возможности организации повторения в курсе геометрии 7-9 классов.
Поставленная цель определила следующие задачи исследования:
1. изучить учебно-методическую и психолого-педагогическую литературу по теме исследования;
2. определить требования к организации повторения;
3. рассмотреть различные подходы к классификации видов повторения;
4. выделить основные формы и методы повторения;
5. перечислить требования к подготовке уроков повторения.
Гипотеза исследования: систематическая организация повторения при изучении геометрии в 7-9 классах, в соответствии с выделенными требованиями, видами и формами будет способствовать более прочному усвоению материала, его обогащению и расширению.
Вз1 Требования к организации повторения
Чтобы обеспечить прочность знаний и навыков, приобретаемых учащимися в процессе изучения математики, нужно правильно организовать повторение, т. е. возвращение к уже пройденному материалу, преследуя две цели, а именно: окончательную доработку программного материала, его, так сказать, отшлифовку, и вместе с тем его закрепление в памяти учащихся.
Цели и время повторения тесно связаны и взаимообусловлены и в свою очередь определяют методы и приемы повторения.
Поэтому задачи повторения и методика его проведения могут быть выражены в трех следующих вопросах, по существу исчерпывающих смысл повторения: Что повторять? Как повторять? Когда повторять?
Первый из этих вопросов касается выбора материала для повторения, второй имеет в виду систему и методы повторения, а третий вопрос тесно связан с организацией педагогического процесса.
При планировании повторения необходимо отобрать материал, установить последовательность и время повторения, распределить отобранный материал по урокам, установить формы и методы для осуществления повторения, разумеется, надо учитывать и свойства памяти.
Основные требования к организации повторения должны исходить из целей повторения, специфики математики как учебного предмета, ее методов.
Первое требование к организации повторения, исходящее из его целей, это определение времени: Когда повторять? Самый общий ответ на поставленный вопрос таков: повторение следует проводить в течение всего учебного года. Оно должно осуществляться по принципу: ВлУчить новое, повторяя, и повторять, изучая новоеВ» (В. П. Вахтеров) [3].
Это не означает, однако, что нельзя специально отводить уроки для повторения, скажем, для таких вопросов программы, которые трудно усваиваются и которые вместе с тем не всегда удается увязать с текущим материалом.
План повторения и выбор тем для повторения учитель должен составлять в каждом отдельном случае на основании общих теоретических соображений с учетом того, как усвоен учащимися материал соответствующих разделов.
К сказанному добавим еще то, что характер урока математики в связи с переходом учащихся из одного класса в другой значительно меняется.
В старших классах существенно перестраивается закрепление и повторение учебного материала. Увеличивается объем фактического материала, выносимого на закрепление и повторение; поурочное закрепление в ряде случаев переходит в тематическое или перерастает в обобщающее повторение, увеличивается доля самостоятельности учащихся при закреплении и повторении.
Второе требование к организации повторения должно отвечать на вопрос: Что повторять? Исходя из высказываний классиков педагогики, положительного опыта дореволюционной и советской школ, можно выдвинуть следующие положения при отборе учебного материала по различным видам повторения:
1. Не следует повторять все, ранее пройденное. Нужно выбрать для повторения наиболее важные вопросы и понятия, вокруг которых группируется учебный материал.
2. Выделять для повторения такие темы и вопросы, которые по трудности своей недостаточно прочно усваиваются.
3. Выделять для повторения надо то, что необходимо обобщить, углубить и систематизировать.
4. Не следует повторять все в одинаковой степени. Повторять основательно надо главное и трудное. При отборе материала для повторения необходимо учитывать степень его связи с вновь изучаемым материалом. [3]
Третье требование к организации повторения математики должно отвечать на вопрос, как повторять, т. е. осветить те методы и приемы, которыми должно осуществляться повторение. Методы и приемы повторения должны находиться в тесной связи с видами повторения.
При повторении необходимо применять различные приемы и методы, сделать повторение интересным, путем внесения? как в повторяемый материал, так и в методы изучения некоторых элементов новизны.
По поводу полезности многообразия методов и приемов весьма удачно выразился немецкий математик-педагог Керр: ВлЛучше одну теорему разобрать десятью способами, чем десять теорем одним способомВ» [3]. К сожалению, этому хорошему принципу следуют далеко еще не все преподаватели математики.
Только разнообразием методов повторения можно устранить то противоречие, которое возникает, с одной стороны, ввиду отсутствия желания у части учащихся повторять то, что ими усвоено однажды, а с другой тАФ в силу необходимости повторять с целью углубления, обобщения и систематизации ранее изученного материала.
Для успешности повторения необходимо соблюдать следующие условия:
1. Повторять надо в течение всего учебного года, т. е. чтобы повторение не было работой от случая к случаю, чтобы повторение входило органической частью в саму методику изучения математики.
2. Должна быть четкая целеустремленность в работе, сознательное отношение учащихся к повторению, осознание ими задач и результатов, которых они должны добиться при повторении.
3. Тщательно отбирать материал и продумывать планирование его при повторении.
4. Стимулировать самостоятельность и активность в процессе повторения, что достигается разнообразием форм и. методов повторения.
5. Правильно дозировать и распределять материал повторения во времени.
6. Соблюдать установку: ВлУчить, чтобы усвоить и запомнитьВ».
Без целевой установки даже многократное повторение может не дать желаемого результата.
7. Органически связывать и продумывать сочетание отдельных видов повторения. Основные виды повторения должны дополнять друг друга, представлять стройную систему педагогически целесообразного повторения.
Работа на уроках повторения и на уроках первичного усвоения различна. Это объясняется своеобразием работы ученика по усвоению нового материала от работы при повторении пройденного, усвоенного уже однажды. Повторением, которое должно помочь учителю в приведении в систему знаний и умений учащихся, мы должны:
а) устранить недочеты в знаниях учащихся;
б) углубить и расширить знания учащихся по данному вопросу;
в) предупредить забывание основного содержания материала;
г) воспроизвести ранее пройденный материал на более высокой ступени в новых связях и комбинациях;
д) обобщить, систематизировать и окончательно закрепить наиболее существенное из учебного материала.
При повторении математики значительную часть времени приходится уделять теории, так как у учащихся возникает много вопросов, требующих более полного и глубокого освещения.
8. Уроки повторения должны быть продуманы как с точки зрения содержания, так и организации их. Постановка самих вопросов и разбор упражнений по своей форме и характеру должны заставлять несколько по-иному осмысливать прежний материал. [3]
Различные виды повторения тесно взаимодействуют; от своевременного и успешного проведения одного из видов повторения, например тематического или текущего, зависит продолжительность и успешность повторения другого вида тАФ заключительного повторения или повторения в конце учебного года. Перейдем к краткой характеристике видов повторения.
Вз2 Виды повторения.В существующей методической литературе, в той или иной мере систематизирующей вопросы повторения школьного курса математики, встречается различная терминология при классификации видов повторения.
Наиболее часто встречается следующая классификация видов повторения:
1. Повторение в начале учебного года.
2. Текущее повторение всего, ранее пройденного:
а) повторение пройденного в связи с изучением нового материала (сопутствующее повторение);
б) повторение пройденного вне связи с новым материалом.
3. Тематическое повторение (обобщающее и систематизирующее повторение законченных тем и разделов программы).
4. Заключительное повторение (организуемое при окончании прохождения большого раздела программы или в конце учебного года). [2]
Охарактеризуем более подробно каждый и выделенных видов.
2.1.
Повторение пройденного в начале года
При повторении в начале учебного года на первый план должно выдвигаться повторение тем, имеющих прямую связь с новым учебным материалом. Новые знания, приобретаемые на уроке, должны опираться на прочный фундамент уже усвоенных.
При повторении в начале года необходимо наряду с повторением тем, тесно связанных с новым материалом, повторить и другие разделы, которые пока не примыкают к вновь изучаемому материалу. Здесь необходимо сочетать обе задачи: провести общее повторение в порядке обзора основных вопросов из материала прошлых лет и более глубоко повторить вопросы, непосредственно связанные с очередным материалом по программе нового учебного года.
Само повторение следует проводить как в классе, так и дома. При решении вопроса, какой материал должен быть повторен в классе и какой оставлен учащимся для самостоятельного повторения дома, надо исходить из особенностей материала. Наиболее трудный материал повторять в классе, а менее трудный давать на дом для самостоятельной работы.
Например, в IX классе на уроках вводного повторения следует повторить понятия вектора, суммы и разности векторов, произведения вектора на число, их свойства. Полезно также повторить некоторые свойства треугольников и четырехугольников: теорему Пифагора, свойство средней линии треугольника, формулы вычисления площади треугольника, понятия медианы, биссектрисы и высоты треугольника, понятия параллелограмма и трапеции, свойства и признаки параллелограмма, ромба, прямоугольника. Цель этого повторения напомнить учащимся сведения, необходимые для изучения геометрии в IX классе.
Повторение можно организовать в ходе решения следующих задач:
1. В треугольниках ABC и AlBlCl дано: АВ = А1В1AC = A1C1, точки D и Dl лежат соответственно на сторонах ВС и В1С1, AD = A1Dl. Докажите, что данные треугольники равны, если AD и A1D1. а) высоты; б) медианы.
2. Докажите, что центр окружности, вписанной в равнобедренный треугольник, лежит на высоте, проведенной к основанию.
3. Докажите, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к его основанию, или на ее продолжении.
4. Докажите, что треугольник является равнобедренным, если две его медианы равны.
5. Докажите, что если в треугольнике две высоты равны, то центр вписанной в него окружности лежит на одной из медиан этого треугольника, а центр описанной окружности тАФ на той же медиане или ее продолжении.
6. Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
7. Докажите, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.
8. Найдите длины отрезков, соединяющих середины сторон трапеции с равными диагоналями, если ее основания равны 7 см и 9 см, а высота равна 8 см.
9. Диагонали параллелограмма ABCD пересекаются в точке М. Упростите выражение: a) 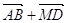 ; б)
; б) 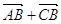 ; в)
; в) 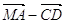 ; г)
; г) 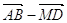 ; д)
; д) 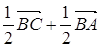 ; e)
; e) 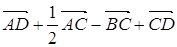 .
.
10. Точка М тАФ середина отрезка АВ, а О тАФ произвольная точка плоскости. Докажите, что 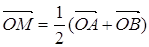 .
.
11. Точки М и Р тАФ середины диагоналей АС и BD трапеции ABCD с основаниями AD и ВС. Докажите, что 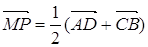 .
.
12. Даны попарно неколлинеарные векторы 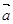 ,
, 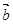 и
и 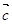 . Постройте векторы: a)
. Постройте векторы: a) 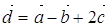 ; б)
; б) 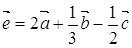 .
.
13. Вычислите площадь треугольника ABC, если АВ = 8,5 м, AC = 5 м, высота AH = 4 м и точка H лежит на отрезке ВС.
14. Вершины четырехугольника ABCD являются серединами сторон четырехугольника, диагонали которого равны 6 дм и пересекаются под углом 60В°. Вычислите площадь четырехугольника ABCD.
Из предложенного набора задач в классе можно решить задачи 1, 2, 4, 6, 8, 9, 11, 13. Остальные задачи на дом.
При решении задачи 1 (б) полезно обратить внимание учащихся на прием Влудвоения медианыВ» тАФ откладывание на продолжении медианы AD за точку D отрезка, равного медиане.
2.2.
Текущее повторение ранее пройденного
Текущее повторение в процессе изучения нового материала тАФ весьма важный момент в системе повторения. Оно помогает устанавливать органическую связь между новым материалом и ранее пройденным.
Текущее повторение может осуществляться в связи с изучением нового материала.
В этом случае повторяется материал, естественно увязывающийся с новым материалом. Повторение здесь входит составной и неотъемлемой частью во вновь изучаемый материал.
Например, учителю предстоит на уроке геометрии доказать теорему о сумме внутренних углов треугольника. Готовясь к уроку, он в своем сознании припоминает те положения, которые необходимы для доказательства этой теоремы. Такими положениями являются: 1) величина развернутого угла, 2) понятие об углах, образующихся при пересечении двух параллельных прямых третьей, 3) неизменность суммы от замены ее слагаемых равными им слагаемыми.
У учителя эти положения расположены в определенной логической связи, необходимой для установления свойств внутренних углов треугольника. У учеников эти представления частично забыты, а другая часть находится в произвольном порядке, не подчиненном какому-либо требованию. Задача учителя состоит в том, чтобы, организуя текущее повторение, путем словесного воздействия и иллюстраций на чертеже, восстановить в памяти забытые учащимися положения и расположить их в том порядке, как они расположены у него.
Для этого он выполняет обычную, но заранее продуманную работу тАФ повторяет то из пройденного материала, что необходимо для доказываемой теоремы. Это он осуществляет путем беседы и постановки перед учащимися ряда вопросов. Например, перед доказательством теоремы о сумме углов треугольника ученикам можно задать такие вопросы:
1. Какой угол называется развернутым?
2. Чему равна градусная мера развернутого угла?
3. Назовите пары углов, которые образуются при пересечении двух параллельных прямых секущей. Какими свойствами они обладают?
Учитель своими вопросами приводит в движение полученные ранее учениками представления, систематизирует их и подготавливает учеников к пониманию доказательства теоремы.
Под руководством учителя ученики на уроке воспроизводят ранее изученный ими необходимый материал. В результате этого доказательство новой теоремы воспринимается учащимися легко, а дальнейшая работа учителя тАФ воспроизведение доказанного и упражнения тАФ обеспечивает вторичное осмысливание теоремы и ее закрепление.
Во втором случае вне связи с новым материалом, когда повторяемый материал не находит естественной увязки с новым и его приходится повторять на специальных уроках.
Повторение пройденного вне связи с новым материалом необходимо весьма тщательно продумать. Удачный подбор материала, установление его последовательности, важность нового подхода к прошлому материалу, введение элементов новизны в повторяемый материал, продуманная организация работы тАФ все это необходимо учитывать при подготовке к рассматриваемому виду повторения.
При текущем повторении вопросы и упражнения могут быть предложены учащимся из различных разделов программы.
Текущее повторение осуществляется в процессе разбора упражнений, включается в домашнее задание. Оно может быть проведено как в начале или в конце урока, так и во время опроса учащихся.
Текущее повторение дополняется сопутствующим повторением, которое нельзя строго планировать на большой период. Сопутствующее повторение не вносится в календарные планы, для него не выделяется специальное время, но оно является органической частью каждого урока. Сопутствующее повторение зависит от материала, привлекаемого для изучения очередного вопроса, от возможности установить связи между новым и старым, от состояния знаний учащихся в данный момент. Успех сопутствующего повторения в значительной степени обусловливается опытом и находчивостью учителя. Сопутствующим повторением учитель по ходу работы устраняет неточности в знаниях, напоминает вкратце давно пройденное, указывает их связь с новым.
Регулярно занимаясь такого рода сопутствующим повторением старого в классе, учитель приучает своих учеников проводить его и при самостоятельной работе дома путём наведения надлежащих справок. Сопутствующее повторение ведётся не только при изучении нового теоретического материала, но и при решении задач: ознакомившись с условием задачи, надо вспомнить точный смысл тех терминов, какие встречаются в её тексте. Подобная ВлмобилизацияВ» надлежащего круга своих сведений имеет первостепенное значение для успешного решения задачи и вместе с тем является важной формой работы по повторению. Само собой разумеется, что использование учебника и старых записей в тетрадях должно при этом всячески поощряться: если ты такую-то вещь позабыл, сумей найти в книге или в тетради соответствующее место.
По цели и по времени проведения текущее и сопутствующее повторения ближе друг к другу, нежели обобщающее и заключительное повторения, которые направлены не столько к закреплению математических фактов, сколько к их систематизации.
2.3.
Тематическое повторение
В процессе работы над математическим материалом особенно большое значение приобретает повторение каждой законченной темы или целого раздела курса.
При тематическом повторении систематизируются знания учащихся по теме на завершающем этапе ее изучения или после некоторого перерыва.
Для тематического повторения выделяются специальные уроки, на которых концентрируется и сообщается материал одной какой-нибудь темы или раздела программы.
В процессе работы над темой вопросы, предлагаемые учащимся по каждому разделу, следует вновь пересмотреть: оставить наиболее существенные и отбросить более мелкие. Обобщающий характер вопросов при тематическом повторении отражается и на их количестве. Учителю приходится основной материал темы охватить в меньшем числе вопросов. Последнее обстоятельство требует от учителя тщательной подготовки к такому повторению.
Повторение на уроке проводится путем беседы с широким вовлечением учащихся в эту беседу. После этого учащиеся получают задание повторить определенную тему и предупреждаются, что будет проведена контрольная работа или зачет.
Контрольная работа должна включать все основные вопросы по изученной теме. После выполнения контрольной работы проводится разбор характерных ошибок и организуется повторение для их устранения.
При тематическом повторении полезно составлять итоговые схемы. Таблица или схема экономно и наглядно показывает общее для понятий, входящих в данную тему, их взаимосвязь в логической последовательности, отношение вида к роду и т. д.
Процесс составления таблиц в одних случаях, подбор и запись примеров после анализа готовой таблицы в других случаях являются одновременно и формами письменных упражнений при обобщающем и систематизирующем повторении [8].
Последовательное изучение различных особых случаев при повторении весьма полезно закончить их классификацией, что поможет учащимся яснее различить отдельные случаи и сгруппировать их по определенному признаку.
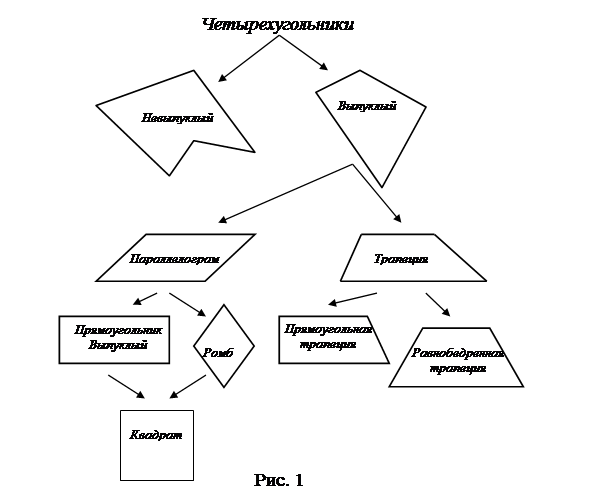 Так, например, повторение темы ВлЧетырехугольникиВ» можно закончить составлением следующей схемы (рис. 1).
Так, например, повторение темы ВлЧетырехугольникиВ» можно закончить составлением следующей схемы (рис. 1).
Далее можно предложить рассмотреть свойства четырехугольников и доказать их в той последовательности, в которой эти четырехугольники расположены в схеме; установить, что каждый последующий четырехугольник обладает всеми свойствами ранее стоящих четырехугольников; установить, сколько и какие элементы необходимы для построения каждого из указанных четырехугольников; объяснить, почему число данных для построения каждого четырехугольника уменьшается от пяти для четырехугольника в общем виде, до одного тАФ для квадрата.
В старших классах можно сообщить учащимся, что для построения многоугольника необходимо (вообще говоря) иметь 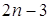 данных (в числе которых, по меньшей мере, один, линейный элемент) и что это число уменьшается в зависимости от его вида.
данных (в числе которых, по меньшей мере, один, линейный элемент) и что это число уменьшается в зависимости от его вида.
Например, чтобы Влпостроить треугольник, надо иметь 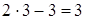 элемента; четырехугольник тАФ
элемента; четырехугольник тАФ 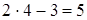 элементов; шестиугольник тАФ
элементов; шестиугольник тАФ  элементов и т.д.
элементов и т.д.
Умея классифицировать четырехугольники (и вообще понятия), учащиеся лучше поймут связь между свойствами различных видов четырехугольника. Они запомнят, что свойства каждого вида сохраняются для всех видов, стоящих на более низких ступенях деления. Классификация понятия является хорошим средством для систематизации знаний учащихся и поэтому заслуживает большего внимания, чем ей уделяют в школьной практике.
Такое глубокое повторение имеет большую ценность и дает больший эффект, чем обычное повторение того, что приводится в учебнике. При таком повторении темы она предстает перед глазами учащихся как стройная цепь логически связанных понятий, каждое определение перестает быть случайным набором слов и связей [3].
Результат такого анализа несомненен
Таким же образом можно построить повторение многих разделов курса. В систему упражнений на повторение темы ВлЧетырехугольникиВ» могут быть включены такие вопросы:
1. Можно ли построить параллелограмм: 1) из четырех неравных отрезков, 2) из двух равных и двух неравных отрезков, 3) из четырех попарно равных отрезков?
2. Определяется ли параллелограмм: 1) двумя смежными сторонами, 2) его стороной и двумя прилежащими к ней углами, 3) его двумя диагоналями, 4) одной диагональю и двумя углами, заключенными между диагоналями, 5) одной диагональю и двумя углами, на которые она делит угол параллелограмма?
Сколькими и какими элементами определяется параллелограмм?
3. Указать условия: 1) необходимые, 2) достаточные, 3) необходимые и достаточные для того, чтобы четырехугольник был параллелограммом.
4. Достаточно ли равенства: 1) одной пары, 2) обеих пар противоположных углов четырехугольника для того, чтобы он был параллелограммом?
5. Для того чтобы параллелограмм был ромбом, достаточно ли, чтобы одна из его диагоналей служила биссектрисой одного из его углов? А в случае четырехугольника?
6. Внутри, какого параллелограмма существует точка, равноотстоящая: 1) от всех его вершин, 2) от всех его сторон?
7. Построить параллелограмм по высоте и диагонали. Сколько решений имеет задача?
8. Построить прямоугольник по диагонали и сумме двух других сторон.
9. Построить параллелограмм по двум сторонам и высоте.
10. Построить квадрат по диагонали.
Тематическое повторение непременно должно предшествовать заключительному повторению в конце четверти или учебного года. Без выполнения этого этапа повторения невозможно успешное осуществление заключительного повторения.
2.4.
Заключительное повторение
Повторение, проводимое на завершающем этапе изучения основных вопросов курса математики и осуществляемое в логической связи с изучением учебного материала по данному разделу или курсу в целом, мы будем называть заключительным повторением.
Цели тематического повторения и заключительного повторения аналогичны, материал повторения (отбор существенного) весьма близок, а приемы повторения в ряде случаев совпадают.
Заключительное повторение в конце учебного года проводится также по темам, однако здесь из темы берется наиболее существенное, материал темы более суживается. Если при тематическом повторении сравнение проводится в рамках этой темы, то при заключительном повторении сравнение математических явлений проводится на более широком материале, и путем такого сравнения учащимся показывается связь между разделами курса.
Такое повторение способствует большему осознанию пройденного, указывает на связь различных разделов курса и одновременно дает возможность обозреть большой материал, создавая представление о системе математики.
Заключительное повторение должно помочь учащимся обобщить известные им знания, обозреть полученные знания в определенной идейно направленной системе, выявить внутренние логические связи между соответствующими отделами предмета, прочно закрепить пройденное.
Таким образом, заключительное повторение учебного материала преследует цели:
1. Обозрения основных понятий, ведущих идей курса соответствующего учебного предмета; напоминания в возможно крупных чертах пройденного пути, эволюции понятий, их развития, их теоретических и практических приложений.
2. Углубления и по возможности расширения знаний учащихся по основным вопросам курса в процессе повторения.
3. Некоторой перестройки и иного подхода к ранее изученному материалу, присоединения к изученному материалу предшествующих лет обучения новых знаний допускаемых программой, с целью его углубления [3].
Уроки по заключительному повторению, как и любой другой урок, должны быть весьма тщательно продуманы как с точки зрения содержания, так и организации их. При этом они могут быть проведены по плану, не совпадающему с планом первоначального изучения. На уроках заключительного повторения должны широко использоваться сопоставления, сравнения и аналогии; постановка самих вопросов по своему характеру должна заставлять несколько по-иному осмысливать прежний материал.
Рассматривая вопросы организации повторения, нельзя увлекаться внесением новизны. Элементы новизны, вносимые при заключительном повторении, не должны наслаивать на основной материал новые, еще не осознанные факты, в равной мере это замечание относится к чрезмерному разнообразию уроков повторения; повторение нельзя отрывать от тех методов, которыми учитель пользовался на обычных уроках [3].
Примером такого вида повторения может служить заключительное повторение курса планиметрии. Это повторение преследует цель систематизировать и обобщить ранее изученные свойства плоских фигур.
Систематизацию знаний и умений, учащихся удобно построить в три этапа.
На первом этапе рассматривается учебный материал, отражающий свойства одной из основных фигур планиметрии тАФ треугольника: повторяются теоремы о свойствах и признаках различных треугольников, в результате чего систематизируются умения учащихся проводить доказательные рассуждения.
На втором этапе повторения учебный материал группируется вокруг многоугольников. Особенностью второго этапа является отработка умений учащихся проводить поиск логических закономерностей и обоснований свойств геометрических фигур на более сложных, по сравнению с первым этапом, геометрических конфигурациях. Кроме того, здесь неизбежно еще раз повторяются свойства треугольников.
На третьем этапе повторяются свойства окружности (круга) и ее элементов. Этот этап подводит итог изучения курса планиметрии.
Содержание повторения
Первый этап
1. Определение треугольника и его элементов.
2. Понятие о равных треугольниках.
3. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников.
4. Свойство углов при основании равнобедренного треугольника. Признак равнобедренного треугольника. Свойство медианы равнобедренного треугольника, проведенной к основанию.
5. Сумма углов треугольника. Внешний угол треугольника и его свойства.
6. Средняя линия треугольника. Теорема Фалеса.
7. Теорема Пифагора. Следствия из теоремы Пифагора. Решение прямоугольных треугольников.
8. Признаки подобия треугольников.
9. Решение и построение треугольников. Теорема синусов. Теорема косинусов. Неравенство треугольника. Векторы.
10. Площадь треугольника.
Учебный материал этого этапа относится в основном к началу изучения курса планиметрии. Отсюда вытекает необходимость напомнить учащимся некоторые логические рассуждения. Например, схему доказательства от противного, структуру прямого и обратного утверждении, что такое свойство фигуры и что такое признак. К тому же треугольник является одной из основных фигур в планиметрии, поэтому многие факты: определения, формулировки теорем, формулы для вычисления элементов треугольника хорошо известны учащимся. Исходя из этого, можно за основную форму организации повторения на первом этапе принять обзорные лекции, в которых следует кратко осветить весь теоретический материал, обращая внимание на логику и поиск доказательств.
Лекции иллюстрируются и дополняются решением задач: на лекции вместе с учителем либо самостоятельно на специально выделенных уроках.
Второй этап
1. Определение параллелограмма. Признаки и свойства параллелограмма Определение прямоугольника. Свойство диагоналей прямоугольника. Определение ромба. Свойство диагоналей ромба. Квадрат Трапеция, средняя линия трапеции
2. Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника Внешний угол многоугольника Правильные многоугольники.
3. Площадь прямоугольника, параллелограмма, трапеции, произвольного многоугольника.
Так как материал этого этапа в основном использует свойства треугольника, повторение которых прошло на первом этапе, рекомендуется проведение уроков в виде бесед, в ходе которых учащиеся под руководством у
Вместе с этим смотрят:
WEB-дизайн: Flash технологии
РЖiрархiчна структура управлiння фiзичною культурою i спортом в Хмельницькiй областi у м. КамтАЩянець-Подiльському
РЖгрова дiяльнiсть в групi продовженого дня
РЖнновацiйнi методи навчання на уроках зарубiжноi лiтератури
РЖнтенсифiкацiя навчального процесу у вищiй школi