Розвиток умiнь розвтАЩязувати задач на пропорцiйне дiлення у початковiй школi

ЗМРЖСТ

ВСТУП

РОЗДРЖЛ 1. ЗАГАЛЬНРЖ ПИТАННЯ НАВЧАННЯ РОЗВтАЩЯЗУВАННЯ ЗАДАЧ

1.1 Система арифметичних задач у програмi з математики в початковiй школi

1.2 Ступенi роботи над текстовими задачами

РОЗДРЖЛ 2. МЕТОДИЧНА РОБОТА НАД ЗАДАЧАМИ НА ПРОПОРЦРЖЙНЕ ДРЖЛЕННЯ

2.1 Види задач на пропорцiйне дiлення та способи iх опрацювання

2.2 Формування умiнь розвтАЩязувати задачi на пропорцiйне дiлення

2.3 Результати експериментального дослiдження

ВИСНОВКИ

СПИСОК ВИКОРИСТАНОРЗ ЛРЖТЕРАТУРИ

ВСТУП

Актуальнiсть теми. Демократизацiя освiти вимагаi вiд педагогiчноi науки нових шляхiв удосконалення навчально-виховного процесу. тАЮОсвiта ХХРЖ столiття тАУ це освiта для людинитАЭ, - зазначено в Концепцii 12-рiчноi загальноосвiтньоi школи. ВлПрiоритетним напрямком оновлення змiсту навчально-виховного процесу i гуманiзацiя освiти, що базуiться на гуманiстичних цiнностяхВ» [53, 47]. Ось чому авторитарнотАУдисциплiнарнi моделi навчання змiнюються на Влособистiсно-орiiнтованi, суттiвими ознаками яких i навчання i виховання особистостi з урахуванням усiх iндивiдуальних та фiзiологiчних процесiв, якi протiкають в органiзмi дитиниВ» [36, 19]. Це створення умов для творчостi, саморозвитку та самовиявлення особистостi молодшого школяра.

Особистiсне зорiiнтоване навчання i виховання i перспективним, оскiльки воно виходить iз самостiйностi особистостi, ii духовностi i суверенностi. Його метою i формування людини як неповторноi особистостi, творця самого себе i своiх обставин. Сучасна школа матиме справу з iндивiдуальнiстю, самобутнiстю особистостi, оскiльки iндивiдуальнiсть виявляiться головним принципом етики i мусить вступати керiвним методологiчним положенням у вихованнi i навчаннi.

У системi загальноi середньоi освiти одне iз основних мiсць займаi початкова школа, де закладаiться фундамент розумових, моральних та емоцiйно-вольових якостей особистостi. Курс математики початкових класiв i основою для осмисленого засвоiння математичних знань, формування умiнь i навичок, а також i отримання математичноi освiти в цiлому [55, 103].

Важливу роль у курсi математики початковоi школи вiдiграють задачi. Вони, з одного боку, складають специфiчний роздiл програми, змiст якого учнi мають засвоiти, з другого тАУ виступають як дидактичний засiб навчання, виховання i розвитку школярiв.

До проблеми розвтАЩязування задач при вивченнi математики тiiю чи iншою мiрою зверталися вiдомi методисти. Психологiчний та методичний аспект процесу розвтАЩязування задач дослiджували: Г.О. Балл, Л.Л. Гурова, С.Д. Максименко, Н.О. Менчинська, Н.А. Побiрченко, З.РЖ. Слiпкань, Л.М. Фрiдман. Психолого-педагогiчнi i методичнi основи диференцiйо-ваного навчання розкрито у працях М.РЖ. Бурди, Ю.З. Гiльбуха, О.С. Дубинчук, С.О. Логачевськоi, О.Л. Савченко, РЖ.РД. Унт та iн.

Особливу увагу розвтАЩязуванню задач як засобу розвитку мислення, формування системи математичних понять, добору задач до пiдручникiв з математики у початковiй школi придiляли М.О. Бантова, Г.В. Бельтюкова, М.В. Богданович, М.М. Левшин, М.Г. Моро, Я.А. Король, Л.П. Кочiна, А.С. Пчолко, Н. Уткiна та iн.

Серед системи задач, якi i предметом вивчення у початковому курсi математики, важливе мiсце займають задачi на пропорцiйне дiлення. РозвтАЩязування задач на пропорцiйне дiлення Влспрямоване на формування в учнiв системи математичних знань, вироблення вмiнь i навичок математичного моделювання, обчислення, розвитку прийомiв розумовоi дiяльностiВ» [15, 71]. Задачi на пропорцiйне дiлення Влдопомагають розкрити опосередкованi звтАЩязки математики з навколишнiм середовищем i практичною дiяльнiстю людей, реалiзувати пiзнавальнi й виховнi функцii навчанняВ» [52, 43]. Процес розвтАЩязування таких задач сприяi формуванню таких розумових дiй як аналiз i синтез, конкретизацiя i абстрагування, порiвняння, узагальнення тощо, а також розвитку функцiонального мислення в цiлому. Вiд оволодiння вмiннями розвтАЩязати задачi залежить не лише пiдготовка школярiв з математики на даному етапi навчання, а й осмислення засвоiння систематичних курсiв алгебри, геометрii, фiзики, iнформатики у наступних класах.

Позитивно оцiнюючи наукову i практичну значущiсть дослiджень з даноi проблеми, необхiдно, разом з цим, вiдзначити, що ряд аспектiв формування вмiнь розвтАЩязувати задачi на пропорцiйне дiлення залишилися нерозкритi, зокрема тАУ обсяг теоретичних знань про таку задачу i процес ii розвтАЩязування у початкових класах; визначення рiвнiв програмних вимог до вироблення вмiнь учнiв початковоi школи розвтАЩязувати задачi на пропорцiйне дiлення; добiр рiзнорiвневих завдань, спрямованих на формування вмiнь розвтАЩязувати задачi; способи рацiонального поiднання фронтальноi, груповоi та iндивiдуальноi форми роботи на уроках математики при розвтАЩязуваннi задач на пропорцiйне дiлення.

Отже, актуальнiсть теми зумовлена значущiстю дослiджуваноi проблеми для удосконалення методики розвтАЩязування задач на пропорцiйне дiлення у початковiй школi, яка враховуi особливостi навчальноi дiяльностi учнiв пiд час розвтАЩязування таких задач, психолого-педагогiчнi засади вироблення вмiнь розвтАЩязувати задачi на пропорцiйне дiлення, рiзнорiвневi вимоги до математичноi пiдготовки школярiв.

ОбтАЩiкт дослiдження тАУ процес навчання математики у початковiй школi.

Предмет дослiдження тАУ формування вмiнь учнiв початкових класiв розвтАЩязувати задачi на пропорцiйне дiлення.

Мета дослiдження тАУ проаналiзувати, теоретично обТСрунтувати i експериментально перевiрити добiрку задач на пропорцiйне дiлення на уроках математики у початковiй школi.

Гiпотеза дослiдження: якщо, навчаючи розвтАШязуванню задач на пропорцiйне дiлення, враховувати змiст i операцiйний склад вiдповiдних умiнь, рiвнi програмових вимог до iх формування, психолого-педагогiчнi характеристики молодших школярiв, дидактичнi принципи добору завдань, то це пiдвищить ефективнiсть навчання учнiв розвтАЩязувати задачi даного типу, а отже, рiвень математичного розвитку школярiв загалом.

Завдання дослiдження:

- на основi аналiзу психологiчноi i навчально-методичноi лiтератури, практики навчання зтАЩясувати стан дослiджуваноi проблеми;

- розкрити змiст i операцiйний склад умiнь учнiв розвтАЩязувати задачi на пропорцiйне дiлення;

- визначити особливостi навчальноi дiяльностi учнiв початковоi школи пiд час розвтАЩязування задач на пропорцiйне дiлення;

- зтАЩясувати обсяг теоретичних знань про такий тип задач i процес iх розвтАЩязування;

- розробити добiрку завдань, спрямованих на вироблення вмiнь розвтАЩязувати задачi на пропорцiйне дiлення;

- теоретично обТСрунтувати та експериментально перевiрити удосконалену методику формування вмiнь розвтАЩязувати задачi на пропорцiйне дiлення.

Методи дослiдження.

1. Теоретичнi тАУ системний аналiз психологiчноi i навчально-методичноi лiтератури з проблеми дослiдження (розкриття змiсту, вмiнь i закономiрностей iх формування); семантичний аналiз задач на пропорцiйне дiлення (зтАЩясування структурних компонентiв задачi i звтАЩязкiв мiж ними); моделювання педагогiчних ситуацiй, аналiз та обробка результатiв педагогiчного експерименту (пiдтвердження ефективностi експериментальноi методики);

2. Емпiричнi тАУ спостереження, анкетування, тестування, бесiди з учнями i вчителями, вивчення досвiду вчителiв, узагальнення власного досвiду викладання математики; формуючий експеримент.

Структура дослiдження. Дипломна робота складаiться iз таких основних елементiв: вступ, два роздiли, висновки, список використаноi лiтератури, додатки.

РОЗДРЖЛ 1. ЗАГАЛЬНРЖ ПИТАННЯ НАВЧАННЯ РОЗВтАЩЯЗУВАННЯ ЗАДАЧ

1.1 Система арифметичних задач у програмi з математики в початковiй школi

Основним засобом, який використовуiться при вивченнi математики для формування знань, умiнь i навичок учнiв, i задачi. Задачi являються засобом реалiзацii загальноосвiтньоi, виховноi i розвиваючоi цiлей. Для формування видiлених елементiв теоретичних знань i оволодiння учнями вiдповiдними iх видами дiяльностi необхiдно розглядати систему задач, що забезпечуi засвоiння навчального матерiалу.

За останнi роки в педагогiчнiй психологii, дидактицi й методицi навчання математики були проведенi дослiдження з рiзних проблем теорii задачi. Значний внесок зробили: Н.Г. Амнiiв, Г.О. Балл, М.РЖ. Бурда, Л.Л. Гурова, В.В. Давидов, О.М. Матюшкiн та багато iнших [5, 149-150]. У цих дослiдженнях вирiшуються кардинальнi питання постановки задач, iх структури, методики навчання розвтАЩязання задач, звтАЩязкiв з вiдомим в умовах, коли субтАЩiкт не маi способу (алгоритму) цiii дii.

На думку К.О. Славськоi, задача з психологiчноi точки зору тАУ це не тiльки обтАЩiктивна вихiдна ситуацiя, а насамперед задача, що виникаi для людини, тобто обтАЩiктивна вихiдна проблемна ситуацiя, обтАЩiктивне вихiдне спiввiдношення умов i вимоги, що створюi невiдповiднiсть мiж ними. Задачу мають розглядати як особливу форму пiзнання дiйсностi. Тому вона сама виступаi як обтАЩiкт, що детермiнуi процес мислення людини.

Якщо аналiзувати психологiчний аспект розвтАЩязування задач, то дослiдники вiдмiчають тiсний зв'язок цього процесу з мисленням особистостi [49, 74]. Усi компоненти мислення (змiстовий, операцiйний та процесуальний) виявляються в мисленнiвiй дiяльностi особистостi. Ця дiяльнiсть виникаi i формуiться як процес за умов проблемноi ситуацii i задачi. Первинно виникаi проблемна ситуацiя, тобто конфлiкт, суперечнiсть мiж обставинами та умовами тАУ мiж наявними знаннями i актуальним потребами. Це малоусвiдомлений процес невизначеностi: тАЬЩо не так? Що не таке?тАЭ тощо.

Усвiдомлення проблемноi ситуацii становить уже перший етап у ii розв'язаннi. На другому етапi вiдбуваiться вирiзнення вiдомого i невiдомого. Внаслiдок цього проблемна ситуацiя перетворюiться на задачу [40, 76]. У структурi задачi вирiзняють умову та вимоги. Для характеристики умови використовують такi ознаки, як звичнiсть-незвичнiсть ситуацii, а також характер поставленоi умови (словесний опис, зображення, реальна ситуацiя) i ступiнь вираження в ситуацii суттiвого вiдношення мiж вiдомими i невiдомими величинами, що i ключовим у розв'язаннi задачi.

Задачi мають задум (iдею, змiст). Важливою характеристикою вимог i чiткiсть iх формулювання. Задачу характеризуi також спiввiдношення мiж умовами i вимогами. В умовi можуть мiститися всi елементи; необхiднi для розв'язання задачi, можуть бути зайвi елементи тощо.

Прикладом нашого пiдходу до поняття задачi i трактування, що його дав О.Ф. РДсаулов. Вiн пише: тАЬЗадача тАУ це бiльш-менш визначенi системи iнформацiйних процесiв, неузгоджене або навiть суперечливе вiдношення мiж якими викликаi потребу в iхньому перетвореннi. Суть розвтАЩязання саме i полягаi у пошуках подолання шляхiв такоi неузгодженостiтАЭ [1, 42].

Р.Е. Басангова визначаi задачу як тАЬяк обтАЩiкт розумовоi дiяльностi, що мiстить вимогу деякого практичного перетворення або вiдповiдi на теоретичне питання за допомогою пошуку умов, що дозволяють розкрити звтАЩязки (вiдношення) мiж вiдомими i невiдомими ii елементамитАЭ.

З методичноi точки зору поняття тАЬзадачатАЭ розглядаiться в роботах М.РЖ. Бурди, Ю.М. Колягiна, В.РЖ. Крупiча, Г.РЖ. Саранцева й iн.

П.РЖ. Сорокiн пiд задачею розумii обтАЩiкт розумовоi дiяльностi, що мiстить вимогу i деякi умови, за яких, ця вимога маi бути досягнута. Отже, задача повинна мати такi ознаки: бути носiiм знань i умiнь, а також засобом iх засвоiння; способом органiзацii i керування пiзнавальною дiяльнiстю учнiв; однiiю з форм прояву методiв навчання; засобом звтАЩязку теорii з практикою [56, 13].

Задачi i i предметом i засобом навчання. Вони i основним засобом забезпечення зв'язку навчання iз життям, полiтехнiчного направлення в навчаннi, здiйснення мiжпредметних зв'язкiв всерединi математики i останньоi з iншими навчальними предметами. На уроках математики навчальний процес в бiльшостi випадкiв слiдуi вiд задач до теорii, а потiм вiд теорii до задач: задачi => теорiя => задачi.

Формування умiнь розвтАЩязувати задачi тАУ одне iз головних i складних завдань програми шкiльного курсу математики в початкових класах [3]. Складнiсть цього завдання зумовлена багатьма факторами. Однак найбiльш суттiвим i той, що в методицi навчання математики в початковiй ланцi освiти залишилися нереалiзованими такi загально дидактичнi принципи, як-от: науковостi, послiдовностi, систематичностi, звтАЩязку теорii з практикою, iндивiдуального пiдходу та iн.

Так, ще Я.А. Коменський зазначав, що мiцно засвоюiться лише те, що добре обТСрунтовано. Отже, розвтАЩязання тiii чи iншоi задачi маi бути науково обТСрунтованим. Для цього учнi повиннi знати найелементарнiшу класифiкацiю задач i вмiти визначити, до якого саме виду належить та чи iнша задача [26, 6].

Задача тАУ це Влсформульоване запитання, вiдповiдь на яке можна знайти за допомогою арифметичних дiйВ» [20, 28]. З визначення задачi випливаi, що в нiй обовтАЩязково маi мiститись якесь запитання. Без запитання задачi немаi. Оскiльки вiдповiдь на запитання задачi дiстаiмо в результатi виконання арифметичних дiй, очевидно, в нiй повинна мiститися вимога визначити те чи iнше число (або числа) тАУ шукане i, крiм того, повиннi вказуватися тi числа, за допомогою дiй над якими можна знайти шукане. Тому обовтАЩязковими елементами будь-якоi арифметичноi задачi i невiдоме (шукане) число (чи кiлька таких) i данi числа.

Головна особливiсть задач полягаi в тому, що в них не зазначаiться, яку саме дiю треба виконати над даними числами, щоб дiстати шукане. Тому в текстi задачi потрiбнi непрямi вказiвки на той звтАЩязок, який iснуi мiж даними числами i шуканими i який визначаi добiр потрiбних арифметичних дiй та iх послiдовностi. Це тАУ умова задачi [7, 23]. Умова, яка покликана розкрити звтАЩязки мiж даними i шуканими числами тАУ мiстить числовi i данi задачi.

Учнi, як правило, досить легко засвоюють, що в задачi маi бути не менше вiд двох числових даних. Дiти часто пiдмiняють задачу формулюванням умови i наслiдку, який з неi випливаi. Наприклад, складають такi тАЬзадачiтАЭ: тАЬНа гiлцi сидiло 3 пташки. До них прилетiла ще 1 пташка. Всього стало 4 пташкитАЭ [56, 14].

Отже, головнi елементи задачi тАУ умова i запитання. Числовi (чи буквенi) данi тАУ це елементи умови. Шукане завжди мiститься в запитаннi. Але iнодi задачу сформульовано так, що запитання мiстить у собi частину умови або вся задача викладена у формi запитання.

В навчаннi математицi видiляють найбiльш важливi функцii задач: навчальнi, виховнi, розвиваючi, контролюючi [8, 287-188].

Навчальнi функцii спрямованi на формування у школярiв системи математичних знань, умiнь i навичок (як передбачених програмою, так i таких, що розширяють, поглиблюють ii змiст) на рiзних етапах навчання.

Виховнi функцii спрямованi на формування пiзнавального iнтересу,самостiйностi, навичок навчальноi працi, культури математичноi мови, графiчноi культури.

Розвиваючi функцii спрямованi на розвиток мислення в учнiв, просторових уявлень, на оволодiння ними ефективними прийомами розумовоi дiяльностi.

Контролюючi функцii спрямованi на встановлення рiвня навчання, здiбностi до самостiйного вивчення матерiалу, рiвня математичного розвитку учнiв i сформованостi пiзнавальних iнтересiв.

У зв'язку з великою кiлькiстю видiв математичних задач розглянемо iснуючi iх класифiкацii. Зокрема, у методичнiй лiтературi [1; 4; 7; 9; 20; 35 та iн.] можна знайти наступнi класифiкацii.

1. За кiлькiстю невiдомих у структурi задач. Ю.М. Колягiн пропонуi iх класифiкувати на навчальнi, пошуковi та проблемнi.

2. За характером об'iктiв задачi подiляють на практичнi та математичнi.

3. За вiдношенням до теорii видiляють стандартнi та нестандартнi задачi. У ролi основноi ознаки стандартних задач вказано наявнiсть у курсi математики таких загальних правил i положень, що однозначно визначають програму розв'язання цих задач та виконання кожного кроку цiii програми (тобто мають свiй алгоритм розв'язування). Нестандартнi задачi - це такi, для яких у курсi математики не iснуi загальних правил або положень, що визначають точну програму iх розв'язання.

4. За функцiями у процесi навчання розрiзняють дидактичнi, пiзнавальнi та розвиваючi задачi. Задачi з дидактичними функцiями використовують для пiдготовки учнiв до введення нового матерiалу, а також при його закрiпленнi: вони несуть функцiю застосування теорii, що вивчаiться. Задачi з пiзнавальними функцiями мають за мету вiдпрацювати та поглибити основний змiст математичноi дисциплiни. Задачi з розвиваючими функцiями тАУ це тi, розв'язування яких потребуi певних знань та вмiнь, не передбачених програмою. Саме цi задачi спрямованi на розвиток мислення.

5. Задачi, що стимулюють навчально-пiзнавальну дiяльнiсть; органiзують та здiйснюють навчально-пiзнавальну дiяльнiсть учнiв; задачi, у процесi виконання яких здiйснюiться контроль та самоконтроль ефективностi навчально-пiзнавальноi дiяльностi.

6. Задачi для початковоi школи класифiкують за змiстом: задачi на рух, задачi на пропорцiйне дiлення, на знаходження четвертого пропорцiйного.

7. За характером вимоги у початковому курсi математики видiляють задачi на обчислення, задачi на побудову, задачi текстовi, задачi комбiнованого характеру.

Наведенi класифiкацii дозволяють ширше уявити собi проблеми, пов'язанi з методикою навчання молодших школярiв розв'язувати задачi, спрямовуючи цей процес на розвиток мислення.

Загалом задачi у початковому курсi математики класифiкують на простi i складенi. При цьому до простих належать 25 видiв задач (на розкриття змiсту арифметичних дiй; на розкриття вiдношень мiж числами; задачi, що розкривають звтАЩязки мiж компонентами i результатами арифметичних дiй; задачi на збiльшення (або зменшення) числа на кiлька одиниць ( чи в кiлька разiв) та iн.) [3, 106-107].

Простi задачi часто використовуються початковому курсi математики i при ознайомленнi учнiв з iншими сюжетами задач у справi формування в дiтей уявлень про величини, iх вимiрювання, про звтАЩязки, якi iснують мiж такими величинами, як цiна, кiлькiсть i вартiсть; маса одного предмета, число предметiв i загальна маса; швидкiсть, час i пройдений шлях; довжина i ширина прямокутника та його площа; норма виробiтку за одиницю часу, затрачений час i загальний виробiток, норма витрати яких-небудь матерiалiв на один вирiб, число виробiв i загальна витрата матерiалiв на них тощо [17, 3]. Такi задачi розглядаються в 1-4 класах поступово, в мiру розширення кола величин, що вводяться у звтАЩязку з вивченням вiдповiдних питань i на матерiалi iнших вправ.

Аналогiчно до того, як простi задачi використовуються для створення наочноi опори при розглядi таких питань теорii, як, скажiмо, звтАЩязок мiж компонентами i результатами дii, значна група складених задач допомагаi дiтям усвiдомити властивостi розглядуваних дiй. Це задачi, якi iлюструють властивостi додавання i вiднiмання, що вивчаються в I класi, а також властивостi множення й дiлення, розглядуванi в II тАУ IV класах.

Складенi задачi, як i простi, використовуються i пiд час ознайомлення з деякими новими поняттями, новими випадками дiй, вони допомагають дiтям усвiдомити новi для них поняття дробу числа й iншi питання курсу [23, 51].

Складенi арифметичнi задачi вiдiграють важливу роль у навчаннi дiтей тих загальних прийомiв розумовоi дiяльностi, якi необхiднi для розвтАЩязання будь-якоi задачi:

а) аналiзувати, видiлити вiдоме i невiдоме;

б) встановлювати звтАЩязки мiж даними i шуканим;

в) складати план розвтАЩязування;

г) перекладати залежностi мiж даними i шуканим, сформульованi в задачi словами, на мову математичних виразiв, рiвностей, рiвнянь;

д) виконувати вiдповiднi дii (розвтАЩязувати вiдповiднi рiвняння) i знаходити вiдповiдь на запитання задачi;

е) перевiряти розвтАЩязання [51, 32].

Складенi задачi використовують як наочну конкретну основу для розгляду нових понять, властивостей дiй. Цiiю функцiiю визначаiться й мiсце iх у загальнiй системi курсу: вони вводяться тодi, коли розглядаються вiдповiднi питання, i в такiй кiлькостi, яка потрiбна для пояснення нових питань. При цьому спецiальноi мети навчити дiтей розвтАЩязувати задачi двома способами не ставиться. Важливiше, щоб вони могли розвтАЩязати ii рацiональним способом.

РЖнша група складених задач, що займають велике мiсце в пiдручниках для початкових класiв школи, повтАЩязана з роботою над рiзними кiлькiсними вiдношеннями. Такi задачi вводяться пiсля того, як дiти достатньо засвоять кiлькiснi вiдношення i навчаться застосовувати своi знання пiд час розвтАЩязування простих задач, якi мiстять слова тАЬна стiльки-то (у стiльки-то разiв) бiльше (менше)тАЭ в рiзному контекстi.

Складенi задачi дають можливiсть продовжити i розширити та поглибити роботу, спрямовану на ознайомлення дiтей з рiзними величинами i залежнiстю мiж ними [62, 23].

Група складених задач, повтАЩязаних з необхiднiстю застосувати знання звтАЩязку мiж такими величинами, як цiна, кiлькiсть, вартiсть, займаi важливе мiсце в пiдручниках для всiх чотирьох класiв. Спецiальна увага придiляiться задачам, якi розкривають звтАЩязки мiж цими величинами в I тАУ IV класах [35, 4].

У IIРЖ класi вводиться ряд нових величин (норма витрачання матерiалу на вирiб, число виробiв, загальна витрата матерiалу; норма виробiтку за одиницю часу, витрачений час i загальний виробiток); у IV класi дiти ознайомлюються iз звтАЩязками мiж швидкiстю, часом i вiдстанню при рiвномiрному русi, iз звтАЩязком мiж сторонами прямокутника i його площею. Усi цi новi питання розглядаються не лише на основi практичних робiт, повтАЩязаних iз спостереженнями, вимiрюваннями, а й на матерiалi розвтАЩязування рiзноманiтних сюжетних задач, що показують, для яких практичних питань потрiбнi здобутi знання, вивченi взаiмозвтАЩязки мiж величинами.

Складенi задачi подiляють за кiлькiстю дiй, якою розвтАЩязуiться та чи iнша задача. Це задача на двi, три, чотири дii. Трьома дiями розвтАЩязуються задачi, якi утворилися розширенням задач на двi дii; також до цього типу належать також задачi на знаходження суми двох добуткiв, рiзницi двох добуткiв, рiзницi двох часток i т. iн. [51, 87].

Метою роботи над задачами i не тiльки засвоiння способiв iх розв'язування, а головним чином формування умiнь, необхiдних для самостiйного розв'язування задач програмного мiнiмуму та подальшого навчання. У пiдручниках для 1тАФ4 класiв i такi задачi, якi традицiйно називають типовими, а також задачi з конкретним змiстом. До типових належать задачi на знаходження четвертого пропорцiйного (на спосiб прямого i оберненого зведення до одиницi та спосiб вiдношень), на пропорцiйне дiлення, на знаходження числа за двома рiзницями, на знаходження середнього арифметичного. Методика розв'язування типових задач принципово не вiдрiзняiться вiд розгляду будь-яких iнших задач нового виду, тобто включаi пiдготовку, ознайомлення i розвиток умiнь [7, 29]. Проте деякi особливостi роботи над типовими задачами необхiдно враховувати.

Зазначенi типовi задачi пов'язанi з пропорцiйними величинами. Розв'язування iх ТСрунтуiться на знаннi вiдповiдних зв'язкiв мiж величинами. Ознайомлення з величинами провадиться одночасно з розкриттям зв'язкiв мiж ними. Зв'язки формулюються у виглядi висновкiв. Наприклад, якщо вiдомо цiну i кiлькiсть, то вартiсть можна знайти дiiю множення. Типовi задачi мають деякi характернi ознаки, якi враховуються на пiдготовчому етапi роботи. Необхiдно також враховувати взаiмозв'язки мiж окремими типовими задачами. Особливу увагу слiд придiлити задачам на знаходження четвертого пропорцiйного до трьох даних.

Розв'язування задач на знаходження четвертого пропорцiйного способом зведення до одиницi запроваджуiться в 3 класi. Розгляду задач передуi тривала робота над iх розв'язуванням на визначення цiни, кiлькостi та вартостi. Вона проводиться у виглядi гри "в магазин" [8]. Пiд час гри учнi вчаться розв'язувати задачi на знаходження вартостi. цiни i кiлькостi. Характерною особливiстю в цiй роботi i те, що, аналiзуючи задачi, вчитель вимагаi вiд учнiв пояснення, якi величини вiдомi i якi треба знайти.

Розв'язування задач на знаходження середнього арифметичного ТСрунтуiться на правилi: щоб знайти середнi арифметичне кiлькох чисел, треба iх суму подiлити на кiлькiсть цих чисел. Це правило вводиться на основi аналiзу готового розв'язання задачi.

Ознайомлення дiтей iз задачами на пропорцiйне дiлення проводять у 4 класi. Спочатку вони виконують пiдготовчi завдання [7, 31].

У початковому курсi математики арифметичнi задачi використовуються протягом усiх чотирьох рокiв початкового навчання. Система iх розмiщення, природно, збiгаiться з логiкою розгортання понять, що вводяться, ознайомлення з арифметичними дiями i iх властивостями тощо. Особливiсть задач, якi для цього вiдбираються, максимальна iх простота. Вони мають бути цiлком зрозумiлi, близькi дiтям за сюжетом, просто викладенi, без будь-яких незрозумiлих, нових для дiтей слiв, якi б потребували додаткових пояснень. Саме цiй метi пiдпорядкована бiльша частина задач, широко представлених у програмi i в пiдручниках для кожного року навчання.

Оскiльки в 1 класi дiти вперше ознайомлюються з дiями додавання i вiднiмання, а в 2 з дiями множення i дiлення, то тут передбачаiться використання простих текстових задач, насамперед спрямованих на розкриття змiсту цих дiй. Жодного означення дiй у початкових класах не вводиться, i тому iх змiст дiти мають усвiдомити, головним чином, на основi практичних операцiй з рiзними множинами предметiв i в процесi розвтАЩязування вiдповiдних простих сюжетних задач, що дають змогу перевести цi операцii в план розумових дiй [39, 134].

Отже, добiр i розмiщення текстових задач для 1-4 класiв пiдлягаi логiцi розгляду нових питань арифметичноi теорii i вiдповiдаi вимозi поступового ускладнення завдань, що зумовлюiться деякими особливостями форми подання математичних звтАЩязкiв i вiдношень, якi визначають вибiр арифметичноi дii, необхiдноi для розвтАЩязування задачi. Ускладнювати завдання можна, ввiвши новi величини, розглядаючи з дiтьми новi для них звтАЩязки.

Однiiю з функцiй складених задач i розвиток здобутих знань, удосконалення iх у процесi застосування в змiнених умовах. Але складенi сюжетнi задачi, введено в початковий курс математики не лише для цього. Одна з iх функцiй тАУ навчити дiтей тАЬперекладутАЭ словесно заданих вiдношень i звтАЩязкiв мiж рiзними величинами, числами, на мову математичних виразiв, рiвностей, рiвнянь. Цiй метi пiдпорядкованi i добiр задач, i система iх розмiщення в часi, i методика роботи над ними.

Ця система забезпечуi поступовий перехiд вiд простого до дедалi складнiшого: вiд складання простих виразiв i рiвнянь у процесi розвтАЩязання задач на одну дiю до складання виразiв з 2-3 дiями при розвтАЩязуваннi досить легких за структурою складених задач. Поступове наростання труднощiв у таких вправах можливе тiльки тодi, коли вчитель розумiючи завдання, що стоять перед ним, використовуватиме для цього пропонованi вправи з пiдручника [23, 54].

Лише вчитель може визначити, яку задачу i коли можна запропонувати дiтям, яке завдання доцiльно повтАЩязати з розвтАЩязуванням цiii задачi: в одному разi досить вказати дiю, за допомогою якоi розвтАЩязуiться задача, в iншому тАУ скласти за нею вираз чи рiвняння, ще в iншому тАУ доцiльно розiбрати хiд розвтАЩязування за дiями, послiдовно зтАЩясовуючи роль кожноi з них i коментуючи здобутi результати.

Отже, серед типових складених задач важливе мiсце займають задачi на пропорцiйне дiлення. Саме цей вид задач i предметом нашого дослiдження.

1.2 Ступенi роботи над текстовими задачами

Розв'язати математичну задачу тАУ це значить знайти таку послiдовнiсть загальних положень математики (означень, аксiом, теорем, правил, законiв, формул), використовуючи якi до умов задачi чи до iх наслiдкiв (промiжних результатiв розв'язання), одержуiмо те, що вимагаiться в задачi, - ii вiдповiдь.

Вченими обТСрунтовано, що психологiчною основою формування вмiнь розвтАЩязувати текстовi задачi i основнi положення теорii поетапного формування розумових дiй (О.М. Леонтьiв, П.Я. Гальперiн, Н.Ф. Тализiна та iн.) у синтезi з основними положеннями асоцiативно-рефлекторноi теорii (Д.Н. Богоявленський, РД.Н. Кабанова-Меллер, Н.О. Менчинська та iн.). Умiння розвтАЩязувати текстовi задачi виробляються ефективно, якщо:

1) подавати повну орiiнтовну основу дiй;

2) при первинному поясненнi розгорнуто подавати зразок розвтАЩязування задачi з фiксацiiю складових операцiй;

3) опрацьовувати виконання окремих дiй, якi входять до складу загального вмiння шляхом розвтАЩязання спецiальних вправ;

4) використовувати рiзнi види моделей задачноi ситуацii;

5) забезпечувати рiзнi види дiяльностi (репродуктивну, продуктивну, творчу) та тривалiсть процесу формування вмiння [4, 43].

Робота над задачами не повинна зводитись до формування навичок розвтАЩязування задач спочатку одного виду, потiм другого i т. д. Основна мета тАУ навчити дiтей свiдомо встановлювати певнi звтАЩязки мiж даними i шуканим у рiзних життiвих ситуацiях, передбачаючи поступове ускладнення iх. Щоб добитися цього, вчитель повинен передбачити в методицi навчання розвтАЩязування задач одного виду рiзнi ступенi, якi мають свою мету.

На першому ступенi вчитель готуi дiтей до розвтАЩязування задач розглядуваного виду. На цьому ступенi учнi повиннi засвоiти звтАЩязки, на основi яких вони вибиратимуть дii в процесi розвтАЩязування таких задач.

На другому ступенi вчитель ознайомлюi учнiв з розвтАЩязуванням задач розглядуваного виду. Тут учнi навчаються встановлювати звтАЩязки мiж даними i шуканим i на цiй основi вибирати арифметичнi дii, тобто вони навчаються переходити вiд конкретноi ситуацii, вираженоi в задачi, до вибору вiдповiдноi арифметичноi дii. Внаслiдок такоi роботи учнi ознайомлюються з способом розвтАЩязування задач цього виду.

На третьому ступенi вчитель закрiплюi вмiння розвтАЩязувати задачi розглядуваного виду. На цьому ступенi учнi мають навчитися розвтАЩязувати будь-яку задачу розглядуваного виду незалежно вiд ii конкретного змiсту, тобто вони мають узагальнити спосiб розвтАЩязування задач цього виду [29, 19-20].

Узагальнено структура процесу розвтАЩязування задач подана на рис.

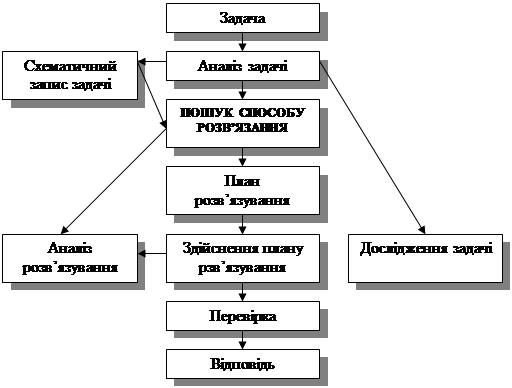Рис. Структура процесу розвтАЩязування задачi

Розглянемо докладнiше методику роботи на кожному з названих ступенiв [8, 213-214].

Пiдготовча робота до розвтАЩязування задач того чи iншого виду (перший ступiнь) залежить вiд того, на який звтАЩязок мiж даними i шуканим треба спиратися пiд час вибору арифметичних дiй. Вiдповiдно до цього виконують спецiальнi вправи.

1. Перед розвтАЩязуванням задач у багатьох випадках виконують операцii над множинами. Пiд час ознайомлення з розвтАЩязуванням бiльшостi простих задач повиннi виконуватись вправи на оперування множинами. Елементами множин мають бути конкретнi предмети (палички, геометричнi фiгури вирiзанi з паперу, самi учнi, рисунки тощо.). Наприклад, до введення простих задач на знаходження суми пропонують вправи на обтАЩiднання множин.

Дiстаньте картинки, де намальованi курчата. (Дiти виконують). На подвiртАЩi було 3 курчат. До них прибiгли ще 2 курчат. Скiльки тепер курчат? (Дiти лiчать картинки). Ми до 3 додали 2 (показуi на картинки) i дiстали 5.

Пiдготовкою до розвтАЩязування задач на вiднiмання буде виконання операцii вилучення частини певноi множини, на множення тАУ виконуються операцii обтАЩiднання рiвно чисельних множин, на дiлення тАУ подiл множин на рiд рiвно чисельних множин.

За допомогою операцii над множинами розкривають змiст виразiв тАЬбiльше на..тАЭ, тАЬменше на..тАЭ, тАЬбiльше в кiлька разiв..тАЭ, тАЬменше в кiлька разiв..тАЭ, що i пiдготовкою для введення задач, повтАЩязаних з поняттям рiзницi та кратного вiдношення.

2. Бiльшiсть арифметичних задач повтАЩязана з величинами (довжина, час, маса, мiсткiсть тощо), тому треба ознайомити дiтей iз цiiю величиною. Також дiтям корисно для подальшоi роботи записувати в окремi зошити чи блокноти значення деяких величин: цiни на окремi товари, швидкостi рiзних видiв транспорту, вiдстанi мiж мiстами чи найближчими селищами тощо.

3. Арифметичнi дii пiд час розвтАЩязування багатьох задач вибирають на основi звтАЩязкiв, якi iснують мiж величинами. Щоб у процесi вибору дiй дiти використовували i усвiдомлювали цi звтАЩязки, потрiбно розкрити звтАЩязки мiж величинами, розвтАЩязуючи задачi на основi iх конкретного змiсту.

Щоб учнi засвоiли той чи iнший звтАЩязок, треба органiзувати цiлеспрямованi спостереження. Щоб розкрити звтАЩязок мiж цiною, кiлькiстю i вартiстю, доцiльно органiзувати екскурсiю в магазин, де учнi ознайомляться з цiною, запишуть цiни на деякi товари в своi довiдники i будуть спостерiгати процес купiвлi-продажу. Потiм на уроцi дiти складуть ряд простих задач на знаходження вартостi за вiдомою цiною i кiлькiстю, розвтАЩяжуть iх, опираючись на знання конкретного змiсту дii множення. Розглянувши розвтАЩязування, учнi помiтять, що коли вiдомо цiну i кiлькiсть, то вартiсть знаходять дiiю множення.

4. РозвтАЩязування складених задач зводиться до розвтАЩязування ряду простих, тому пiдготовкою до розвтАЩязування складених задач буде навчання розвтАЩязування простих задач.

Розгляду кожного окремого виду задач маi передувати спецiальна пiдготовча робота. Провiвши вiдповiдну пiдготовчу роботу, можна перейти до ознайомлення дiтей з розвтАЩязуванням задач розглядуваного виду [20, 28].

У методицi початкового навчання математики видiляють такi етапи розв'язування задач, як ознайомлення iз змiстом задачi, аналiз задачi i вiдшукання плану розв'язування, розв'язання задачi та перевiрка розв'язування. Розглянемо методику роботи на кожному з цих етапiв.

1. Ознайомлення iз змiстом задачi. Усвiдомлення змiсту задачi тАФ необхiдна умова ii розв'язання. Учень не повинен приступати до розв'язування задачi, не зрозумiвши ii умови. Тому ознайомлення з задачею мiстить власне опанування ii змiсту i перевiрки усвiдомлення його дiтьми.

Учень ознайомлюiться з задачею iз слiв учителя або самостiйно. Це, так би мовити, Влкрайнi способиВ». Поряд з ними використовуються Влпромiжнi способиВ», в яких ступiнь самостiйностi учнiв залежить вiд рiвня iхньоi пiдготовленостi i мети розв'язування задачi. Приступаючи до розв'язування задачi, важливо сприйняти ii в цiлому, а потiм вже розбивати на окремi частини [22, 26].

При фронтальному ознайомленнi вчитель читаi (або переказуi) задачу двiчi. Першого разу задачу читають з метою ознайомлення з ii змiстом в цiлому. Другого разу задачу читають частинами i так, щоб кожна частина мiстила певну смислову ВлодиницюВ» тексту. Подiл задачi на частини здебiльшого передбачаi видiлення окремих числових даних ii. Пiд час другого читання доцiльно на дошцi записувати умову. Читаючи задачу, вчитель паузами та iнтонацiiю видiляi числовi данi та слова, що визначають вибiр дii та запитання задачi. Емоцiйне забарвлення голосу допомагаi учням уявити ту життiву ситуацiю, про яку йдеться в задачi. Тому, слухаючи задачу, дiтям не варто слiдкувати очима за текстом пiдручника. Якщо в задачi i маловiдомi дiтям термiни, то iх слiд пояснити заздалегiдь, застосовуючи для цього предметне iлюстрування або малюнки.

Щоб перевiрити, як учнi усвiдомили умову задачi, вчитель задаi учням запитання (за смислом окремих частин) або пропонуi переказати всю задачу. З метою активiзацii контрольного повторення задачi слiд наперед ставити перед учнями те або iнше завдання. Наприклад: ВлПослухайте задачу i повторiть вголос ii запитанняВ», ВлПрочитайте задачу самостiйно i скажiть, що нам вiдомоi про..В». [7, 42]

Розглянутi вимоги стосуються i самостiйного читання задач учнями. Дiти повиннi засвоiти, що в процесi, читання треба запам'ятати або виписати числовi данi i видiлити запитання задачi i найбiльш важливi слова, якi стосуються даних i шуканого чисел, а також з'ясувати незрозумiлi слова.

2. Аналiз задачi i вiдшукання плану ii розв'язування. Учень зможе успiшно розв'язати задачу, якщо розу

Вместе с этим смотрят:

WEB-дизайн: Flash технологии

РЖiрархiчна структура управлiння фiзичною культурою i спортом в Хмельницькiй областi у м. КамтАЩянець-Подiльському

РЖгрова дiяльнiсть в групi продовженого дня

РЖнновацiйнi методи навчання на уроках зарубiжноi лiтератури

РЖнтенсифiкацiя навчального процесу у вищiй школi