Зачетная система при обучении математике
Важным звеном процесса обучения математике является контроль знаний и умений школьников. От того, как он организован, на что нацелен, существенно зависит эффективность учебной работы. Именно поэтому в школьной практике уделяется серьезное внимание способам организации контроля, его содержанию. Многие учителя и методисты ведут большую работу по совершенствованию форм и методов контроля. Эта работа всегда связана со стремлением более полно реализовать цели и задачи школьного математического образования, она отражает те или иные изменения, которые происходят в системе обучения математике [3].
Проведение различных типов уроков помогает не только поддерживать в ученике интерес к предмету, но и побуждать его к действию, раскрывая тем самым потенциальные возможности каждого [4].
В целях повышения ответственности учащихся за результаты своего труда, для развития самостоятельности в овладении знаниями необходимо устранить стереотипность в обучении и воспитании, совершенствовать систему учета знаний учащихся. В этой связи все более широкое распространение в школе получают зачетные формы организации контроля знаний учащихся [1].
1. Уровневая дифференциация
В настоящее время принципиальные изменения в школе связаны в первую очередь с введением дифференцированного обучения. Важнейшим видом дифференциации при обучении во всех классах становится уровневая дифференциация. Ее основная особенность состоит в дифференциации требований к знаниям и умениям учащихся: явно выделяется уровень обязательной подготовки, который задает достаточную нижнюю границу усвоения материала. Этот уровень, безусловно, доступен и посилен всем школьникам. На его основе формируются повышенные уровни овладения курсом. Учащиеся получают право и возможность, обучаясь в одном классе и по одной программе, выбирать тот уровень усвоения, который соответствует их потребностям, интересам, способностям.
Эти уровни, и, прежде всего, уровень обязательной подготовки, должны быть открытыми, т. е. известными ученикам и понятными им. Только в этом случае можно рассчитывать на познавательную активность школьников, на заинтересованность их в результатах своего труда. Ведь если цели известны и посильны, а их достижение поощряется, то для подростка нет ничего естественнее, как стремиться к их осуществлению. Поэтому открытость уровней подготовки является механизмом формирования положительных мотивов учения, сознательного отношения к учебной работе, позволяет опереться на самооценку ученика в выборе индивидуального пути его развития.
Именно такой подход способствует психологическому комфорту ученика в школе, формирует у него чувство уважения к себе и к окружающим, вырабатывает ответственность и способность к принятию решений.
Практическое осуществление уровневой дифференциации не должно означать, что одним ученикам предлагается больший объем материала, а другим меньший. Каждый должен пройти через полноценный учебный процесс, который ни для кого не может быть ограничен требованиями минимума. Иначе и уровень обязательной подготовки не будет достигнут, и учащиеся, потенциально способные на большее, могут быть потеряны. Иными словами, уровень обучения в целом должен превышать уровень обязательных требований. Каждый ученик должен в полном объеме услышать изучаемый материал, увидеть в определенном смысле идеальные образцы деятельности. И одни школьники воспримут эти образцы полностью, присвоят их, сделают своим знанием и опытом, другие тАУ не потеряются в обилии информации, усвоят из нее то, что предусматривается минимальным стандартом.
Возможность выбрать уровень усвоения, в частности ограничиться уровнем обязательных требований при изучении нелюбимых пли трудных предметов, поможет избежать перегрузки школьника. С другой стороны, только освободив ученика от непосильной суммарной учебной нагрузки, мы сможем направить его усилия в область склонностей и интересов, способствуя развитию ребенка, полному раскрытию его способностей.
Реализация уровневого подхода при обучении требует разработки целого комплекса мер, специальной технологии обучения. И, прежде всего, должна быть перестроена система контроля. Контроль и оценка должны отражать принятый уровневый подход.
В процессе обучения контроль, как правило, присутствует на всех этапах, начиная с самых первых моментов в овладении учениками новым материалом и до завершения темы. В данной книге обсуждаются вопросы организации тематической и итоговой проверки математической подготовки школьников в условиях уровневой дифференциации [3].
2. Зачет как основная форма проверки усвоения учебного материала
Для систематического контроля за достижением обязательных результатов обучения в ходе учебного процесса целесообразно выбрать такую форму проверки, как зачет. Зачеты отличаются от традиционной контрольной работы и по системе оценивания (используется не пятибалльная, а двухбалльная шкала), и по характеру проведения (предусматривается необходимость пересдачи в случае отрицательного результата). Именно эти свойства зачета наиболее точно отвечают особенностям проверки и оценки достижения учащимися уровня обязательной подготовки.
Действительно, обязательные результаты обучения тАУ это тот минимум, который необходим для дальнейшего обучения, для выполнения программных требований к математической подготовке учащихся. Поэтому при проверке учителю принципиально важно получить определенный ответ: овладел или не овладел ученик формируемыми умениями на обязательном уровне. Иными словами, здесь наиболее естественной является альтернативная оценка: Влдостиг (да)В» тАУ Влне достиг (нет)В». С другой стороны, мало констатировать, что какой-то конкретный ученик не достиг уровня обязательной подготовки. Цель учителя тАУ добиться того, чтобы каждый овладел важнейшими умениями и навыками. Поэтому, если ученик не справился с зачетом, надо организовать доработку соответствующего материала и его повторную проверку.
Зачет тАУ это специальный этап контроля, целью которого является проверка достижения учащимися уровня обязательной подготовки [3].
Остановимся на нескольких моментах:
1. Зачеты являются весьма нелегким испытанием для школьников, поэтому нельзя злоупотреблять этой формой работы.
В VIII тАУ IX классах должно проводиться по 1тАУ2зачета, в XтАУXI классах тАУ по 2тАУ3 зачета в год.
2. К зачету должна проводиться всесторонняя подготовка. Цель зачета тАУ добиться свободного владения школьниками различными методами, изученными в курсе, укрепить внутрипредметные связи. Для выполнения этой цели нужна как тщательная отработка усвоения содержания каждой отдельной темы, так и опыт объединения изученного в одно целое. Этой цели служат коллоквиумы, опросы, циклы. Этому должны быть посвящены специальные уроки и консультации.
3. Оценивая объем материала, выносимого на зачет, нельзя формально считать Влчисло теоремВ», полагая, что большое количество вопросов автоматически означает высокую трудность зачета. Например, тема ВлИнтегральное исчислениеВ» предполагает активное владение теоремами теории пределов и дифференциального исчисления, поэтому включение их в программу не увеличивает трудность зачета, а, напротив, делает более наглядными основные идеи курса. Следует избегать неоправданного включения в программу зачета теорем с искусственными, не допускающими дальнейших обобщений доказательствами,
4. Программы зачетов могут (и даже должны) ВлпересекатьсяВ». Один и тот же материал, попадая в разные наборы вопросов, обретает дополнительный смысл. Очевидна к тому же польза от многократного повторения [5].
Оценка результатов сдачи зачета осуществляется по двухбалльной шкале: ВлзачтеноВ» тАУ Влне зачтеноВ».
Зачеты проводятся по каждой теме курса. Их содержание отбирается таким образом, чтобы обязательные результаты обучения были представлены максимально полно [3]. Для проведения зачетов выделяются специальные дни, в которые не проводятся уроки по другим предметам [5].
Каждый ученик сдает все предусмотренные планом зачеты.
Зачет считается сданным, если ученик выполнил верно все предложенные ему задачи обязательного уровня. В противном случае (если хотя бы одна задача осталась не решена) оценка ВлзачтеноВ» не выставляется. При этом зачет подлежит пересдаче. Ученик пересдает не весь зачет целиком, а только те виды задач, с которыми он не справился.
При проведении зачетов задачи обязательного уровня, составляющие собственно содержание зачета, могут дополняться более сложными заданиями. За их решение ученику, сдавшему зачет, дополнительно выставляется одна из двух отметок тАУ тАЬ4тАЭ или тАЬ5тАЭ. Таким способом во время зачета можно сочетать проверку обязательных результатов обучения с проверкой на более высоком уровне. Это позволит объективнее и точнее дифференцировать учащихся по уровню их подготовки.
Итоговое оценивание знаний школьника (за четверть, полугодие, год) непосредственно зависит от результатов сдачи зачетов. Оценка является положительной только при условии, если всё зачеты за этот период учеником сданы. Таким образом, даже если все отметки какого-либо ученика тАЬ5тАЭ, но у него не сдан один зачет, в соответствии с условиями принятой системы не может быть выставлена положительная отметка в четверти. В то же время если ученик сдал все зачеты, то он независимо от текущих отметок имеет право на положительную оценку в четверти.
Понятно, что ученик может не сдать тот или иной зачет по разным причинам. Это могут быть случайные, косвенные особенности, или по своим индивидуальным особенностям ученик медленнее других овладевает материалом и т. д. Поэтому на практике целесообразно ввести еще одно условие. Если четверть закончена, а ученику необходимо пересдать какие-либо зачеты, то в случае можно предусмотреть ВлотложеннуюВ» итоговую оценку. Иными словами, ученик не аттестовывается до тех пор, пока не ликвидирует все долги.
Условия организации зачетов позволяют обеспечить в течение учебного года достаточно полную проверку каждого ученика на обязательном уровне. Это достигается тем, что в ходе тематического контроля ставится задача как можно полнее охватить обязательные результаты по этой теме; при этом ученик отчитывается за все темы, изучаемые в курсе.
Может возникнуть вопрос: должен ли сильный ученик сдавать зачет тАУ ведь он, как правило, справляется со значительно более сложными задачами? Конечно, от учителя зависит, принимать или не принимать то или иное положение зачетной системы, сформулированное выше. Однако опыт применения этой системы на практике убеждает нас в том, что через должны пройти все школьники. Во-первых, обязательно участие в зачете всех учащихся делает его более весомым, заставляет серьезнее относиться к подготовке, что положительно влияет на формирование необходимых умений и навыков. Во-вторых, так как результаты зачетов непосредственно связаны с итоговой аттестацией школьников, было бы неправильно освобождать кого-то от зачетов и тем самым ставить учеников в неравные условия. В-третьих, у сильных учеников бывают, и нередко, пробелы именно в основных, фундаментальных умениях. Сосредоточив свое внимание на более интересных для них вопросах, они часто излишне легкомысленно относятся к элементарным опорным задачам. Соответствующие недоработки всплывают именно во время зачета, что позволяет как учителю, так и самому ученику своевременно обратить на них внимание. И, наконец, ученик, уверенно владеющий опорными умениями, не потратит много времени на выполнение задач обязательного уровня. Поэтому у него есть возможность в ходе этого же зачетного урока проявить себя в решении более сложных заданий и получить одну из повышенных отметок.
Условия организации зачетов повышают содержательность и объективность итогового оценивания. Оно в большей степени, чем традиционный способ выведения отметок в четверти, ориентировано на конечный результат. Исчезает ситуация, когда тройка за одну тему закрывает двойку за другую. Отметка тАЬ3тАЭ в четверти совершенно определенно означает, что ученик проявил владение обязательными умениями. На практике изменяется и отношение к отметкам тАЬ4тАЭ и тАЬ5тАЭ. Учителя более строго подходят к их выставлению, стремятся убедиться в том, что подготовка ученика действительно превосходит уровень обязательной подготовки, что учащийся умеет решать более сложные задачи, отвечать на трудные вопросы.
Таким образом, при оценивании знаний учитываются позитивные достижения каждого школьника, а не недостатки в его подготовке [3].
3. Виды зачетов
Систему зачетов в зависимости от склонностей учителя, стиля его работы, особенностей класса и т. д. можно строить по-разному. С помощью зачетов проверяют овладение различными порциями учебного материала. В соответствии с этим их можно разделить на тематические и текущие. Тематические зачеты приводятся в конце изучения темы и направлены на проверку усвоении ее материала в целом. Текущие зачеты проводятся систематически в ходе изучения темы по небольшим, законченным по смыслу порциям учебного материала.
Оба вида зачетов можно проводить, условно говоря, в открытой или закрытой форме. В первом случае учащиеся предварительно знакомятся со списком задач обязательного уровни. Во втором случае этот список в явном виде учащимся не предъявляется. Однако это не означает, что учащимся совсем неизвестно, какие типы задач относятся к обязательным. В ходе изучения материала учитель акцентирует внимание учеников на задачах обязательного уровня, подчеркивая, что подобные им необходимо будет решать на зачете.
Итак, можно выделить следующие четыре вида зачетов: открытый тематический зачет, закрытый тематический зачет, открытый текущий зачет, закрытый текущий зачет [3].
3.1 Тематический зачет
Ø Открытый тематический зачет
Открытый тематический зачет проводится как завершающая проверка по какой-то теме. В начале изучения темы учитель вывешивает в классе или раздает учащимся список задач, отвечающих уровню обязательной подготовки по данной теме, и сообщает, что после ее изучения будет зачет, на котором будет проверяться умение решать задачи подобного типа. Учитель указывает также примерные сроки проведения зачета. Необходимо отметить, что учащихся, а также их родителей полезно заранее (в начале учебного года) ознакомить со всеми особенностями зачетной системы и условиями проведения зачетов.
На специально выделенном уроке проводится зачет. Учащимся предлагается проверочная работа, охватывающая содержание изученной темы. Ее удобно составлять из двух частей. Первая тАУ это собственно задания зачета. Она содержит задачи обязательного уровня, аналогичные тем, которые были приведены в списке обязательных результатов обучения. Вторая тАУ более сложные задачи по проверяемой теме на хорошо подготовленных учеников. Те учащиеся, которые уверенно владеют умением решать задачи обязательного уровня, как правило, к середине урока справляются с ними. Поэтому имеется возможность в ходе этого же урока осуществить проверку на более высоком уровне. Ученики работают в индивидуальном темпе. Те, кто выполнил обязательную, зачетную часть работы, могут приступить к дополнительным заданиям и, решив их, получить, кроме зачета, одну из повышенных оценок. Другие имеют резерв времени для решения задач, включенных в зачет, для исправления ошибок.
Время на пересдачу выделяется на последующих уроках. Например, ученику, не сдавшему зачет, на каком-либо из следующих уроков во время проведении опроса, или проверки домашнего задания, или самостоятельной работы может быть индивидуальное задание, аналогичное тому, с которым он не справился на зачете. Или при устном опросе такой ученик получит задачу из зачета в качестве дополнительного задания [3].
Ø Закрытый тематический зачет
Закрытый тематический зачет отличается от открытого только тем, что список задач, отвечающих уровню обязательной подготовки, учащимся не сообщается. В то же время в ходе изучения материала учитель указывает на обязательные умения, обращает внимание учащихся на задачи обязательного уровня [3].
Составление заданий для тематических зачетов. Приведем один вариант по теме ВлНеравенстваВ». Она состоит из двух частей обязательной и дополнительной. Обязательную часть составляют задачи обязательного уровня, за выполнение которых ученик получает отметку ВлзачтеноВ»; дополнительную часть тАУ более сложные задачи, за выполнение которых ученик может дополнительно получить отметку тАЬ4тАЭ или тАЬ5тАЭ (в зависимости oт объема и качества выполнения этих задач).
Зачет по теме ВлНеравенстваВ»
Обязательная часть.
1. Решите неравенство:
a) 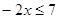 ;
;
b) 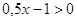 ;
;
c) 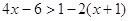 .
.
2. Решить систему неравенств:
a) 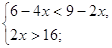
b) 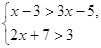
3. Найдите решение двойного неравенства: 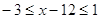 .
.
Дополнительная часть
4) Найдите наименьшее целое число, являющееся решением неравенства
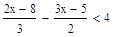
5) При каких с уравнение 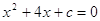 не имеет корней?
не имеет корней?
В обязательную часть включаются задачи из списка обязательных результатов обучения или аналогичные им. Понятно, что в один вариант невозможно включить все задачи списка. Однако для того, чтобы обеспечить как можно большую полноту проверки, надо шире охватить все группы умений, представленных на уровне обязательной подготовки. В приведенной работе присутствуют все основные умения по проверяемой теме: решение линейных неравенств (причем предусмотрены случаи деления обеих частей неравенства как на положительное, так и на отрицательное числа, а также необходимость выполнения некоторых тождественных преобразований), решение систем линейных неравенств с одной переменной, решение систем, записанных в виде двойного неравенства. Поэтому если ученик справился со всеми задачами первой части работы, то можно с уверенностью сказать, что он овладел материалом на уровне обязательной подготовки.
Бывают случаи, когда в одном варианте трудно представить все основные группы задач. Такая ситуация часто складывается, например, в геометрии. Так, тема ВлСумма углов треугольникаВ» включает в себя три фрагмента: ВлПараллельность прямыхВ», ВлСумма углов треугольникаВ», ВлПрямоугольный треугольникВ». В последний входят и признаки равенства прямоугольных треугольников. Поэтому, чтобы охватить весь объем содержания, нужны, по крайней мере, три задачи. Но задачи по геометрии (даже несложные), как правило, более трудоемки, чем по алгебре. В связи с этим можно или увеличить время, отводимое на соответствующий тематический зачет (например, взять два урока), или же пойти по пути составления разных вариантов. В последнем случае в каждый вариант можно включить две задачи, относящиеся к каким-либо двум из указанных трех фрагментов. Например, в одном из них тАУ задачи на признаки параллельности прямых и сумму углов треугольника, в другом тАУ на свойства углов при параллельных прямых и секущей и признаки равенства прямоугольных треугольников. Важно, чтобы были охвачены все группы задач.
Для такого подхода к составлению вариантов особенно благоприятны условия открытого зачета. Готовясь к зачету, ученик знает, что все виды задач войдут в проверку, будут включены в какой-нибудь из вариантов. Какой именно вариант ему достанется, ученик не знает, но ему известно, что, не решив хотя бы одну задачу, он не сдаст зачет. Поэтому учащийся вынужден готовиться по всем обязательным задачам. В случае сомнений по поводу знаний ученика учитель всегда может на зачете предложить ему еще задачу.
Основное назначение дополнительной части тАУ дать учителю возможность дифференцировать учащихся по уровню их подготовки, а также стимулировать школьников, которым хорошо дается математика, к совершенствованию своей подготовки, развитию формируемых умений. Для этой цели нет необходимости обеспечивать полноту охвата материала темы на более высоком уровне. Для выставления ученику повышенной оценки достаточно убедиться в том, что он проявляет полное владение обязательными результатами обучения, то есть имеет хорошую опорную подготовку, и при этом справляется с решением более сложных задач.
Понятно, что при таком подходе необязательно предлагать всем учащимся аналогичные задачи. Поэтому в разные варианты можно включать разные по содержанию задания, важно лишь проследить, чтобы они были примерно одинаковы по уровню сложности. Так, например, в приведенном зачете по теме ВлНеравенстваВ» дополнительная часть содержит два задания. Одно из них требует более развитой по сравнению с обязательным уровнем техники решения неравенств. Другое с технической стороны несложно. Но здесь ученику придется найти способ решения задачи, применить знания из предыдущей темы, иными словами, проявить определенную умственную инициативу и самостоятельность. Таким образом, некоторые ученики могут выполнять оба задания, продемонстрировав широту своей подготовки; другие имеют возможность, выбрав задание, проявить себя в том, в чем они сильнее.
Объем зачета, его обязательной части, а также дополнительных заданий планируется таким образом, чтобы их выполнение было посильно успевающему ученику в отведенное для зачета время.
Можно увеличить число дополнительных заданий, включив резервные и предоставив учащимся возможность выбора.
Необходимо иметь в виду, что к содержанию и уровню сложности дополнительных заданий рекомендуется относиться критически и при необходимости или желании учителя пересматривать их, учитывая особенности класса [3].
3.2 Текущий зачет
Текущие зачеты проводятся несколько раз в ходе изучения темы. От тематических они отличаются тем, что охватывают меньший по объему материал; поэтому, как правило, на их проведение не требуется отводить целый урок. Это могут быть небольшие работы, рассчитанные на 10-20 мин и направленные на проверку одного тАУ двух умений, формируемых в течение нескольких уроков.
Задания для текущих зачетов отбираются таким же образом, как и для тематических. При этом требуется только разбить тему на смысловые фрагменты, по которым и организовать проведение зачетов. Например, тема ВлКвадратный трехчленВ» при обучении по учебнику ВлАлгебра тАУ 8 (С. А. Теляковского) естественно делится на такие разделы: ВлРазложение квадратного трехчлена на множителиВ», ВлГрафик функции у=ах2+bx+cВ», ВлРешение неравенств второй степени. Метод интерваловВ». В соответствии с этим можно провести 3 или 4 зачета, разбив, например, второй раздел на две части: ВлГрафик функции у = ax2+сВ» и ВлГрафик функции y=ax2+bx+cВ».
При этом можно составить несколько аналогичных по содержанию вариантов для зачета. Это целесообразно при составлении зачета по первому и последнему из указанных разделов. Если же раздел содержит большое число типов задач обязательного уровня, то, так же как и в тематических зачетах. При составлении заданий можно составить разные варианты. При этом, однако, важно предусмотреть, чтобы совокупность вопросов охватывались все основное содержание подвергаемого проверке материала и чтобы у каждого ученика были проверены основные виды умений. Так, например, проверяя усвоение графика квадратного трехчлена, необходимо проверить умение строить соответствующий график, а также читать его, предложив каждому ученику ответить на один из вопросов: определить промежутки знакопостоянства функции; найти по графику промежутки возрастания и убывания функции.
Приведем примеры текущих зачетов (обязательные задания) по указанным разделам темы ВлКвадратный трехчленВ».
Зачет № 1. Разложение квадратного трехчлена на множители
Разложите на множители квадратный трехчлен:
Вариант 1. 1) 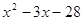 ; 2)
; 2) 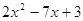 .
.
Вариант 2. 1) 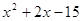 ; 2)
; 2) 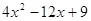 .
.
Вариант 3. 1) 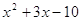 ; 2)
; 2) 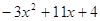 .
.
Вариант 4. 1) 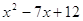 ; 2)
; 2) 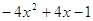 .
.
Зачет № 2. График функции 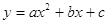
Вариант 1
1) Постройте график функции 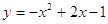 .
.
2) С помощью графика функции определите, при каких значениях 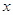
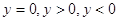 .
.
Вариант 2
1) Постройте график функции 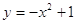 .
.
2) С помощью графика функции определите, при каких значениях 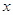 функция возрастает; убывает
функция возрастает; убывает
Вариант 3
1) Постройте график функции 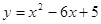 .
.
2) С помощью графика функции найдите, чемe равно значение функции при 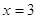 ; при каких значениях
; при каких значениях 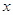
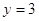 .
.
Вариант 4
1) Постройте график функции 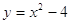 .
.
2) С помощью графика функции найдите те значения 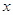 , при которых
, при которых 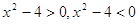 .
.
Зачет № 3. Неравенства второй степени. Метод интервалов.
Решите неравенство:
Вариант 1. 1) 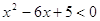 ; 2)
; 2) 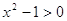 ; 3)
; 3) 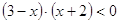 .
.
Вариант 2. 1) 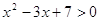 ; 2)
; 2) 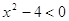 ; 3)
; 3) 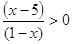 .
.
Вариант 3. 1) 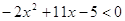 ; 2)
; 2) 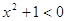 ; 3)
; 3) 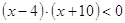 .
.
Вариант 4. 1) 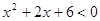 ; 2)
; 2) 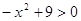 ; 3)
; 3) 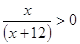 [3].
[3].
4. Подготовка к зачету
Учеников надо специально готовить к зачету. В процессе изучения темы должно отводиться специальное время на формирование и отработку умений решать задачи обязательного уровня. Поэтому при планировании уроков целесообразно предусмотреть такую работу, а в ходе ее проведения на уроке акцентировать на ней внимание учащихся.
В тетрадях учащихся непременно должны быть записи решений задач обязательного уровня. Наблюдения на уроках показывают, что часто при разборе опорных задач записи ведутся только на доске (причем часто это делает сам учитель); ученики делают лишь устные пояснения, не делая никаких записей в тетрадях, а к письменному оформлению решения переходят лишь в сложных случаях. Необходимо заметить, что, записывая важнейшие моменты решения, учащиеся лучше и быстрее запоминают правило, формулу, теорему, усваивают правильную последовательность действий, вырабатывают прочный навык. Поэтому, например, при изучении формул сокращенного умножения решение самых первых примеров на применение формул, а именно заданий типа 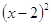 ,
, 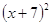 ,
, 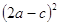 , следует записать в тетрадях. Понятно, что со временем можно перейти и к устному выполнению такого рода упражнений, однако па первоначальном этане их письменное решение необходимо. Кроме того, запись решения опорных задач в тетрадях будет служить ученикам образцом, к которому они могут обратиться при выполнении домашнего задания, при повторении материала, при подготовке к зачету.
, следует записать в тетрадях. Понятно, что со временем можно перейти и к устному выполнению такого рода упражнений, однако па первоначальном этане их письменное решение необходимо. Кроме того, запись решения опорных задач в тетрадях будет служить ученикам образцом, к которому они могут обратиться при выполнении домашнего задания, при повторении материала, при подготовке к зачету.
Целесообразно, чтобы задания, аналогичные задачам контрольного списка, включались также в домашнюю работу, а проверка их выполнения у средне- и слабоуспевающих учащихся была бы обязательной. Такую проверку можно организовать с привлечением сильных учеников.
Конечно, все сказанное не означает, что процесс формирования математических умений ограничивается решением задач обязательного уровня, В ходе обучения ученики решают самые разные задачи, в том числе более сложные: задачи на установление связей между изучаемым материалом и другими разделами курсов, развивающие задачи и т. д. Однако работа над достижением обязательного уровня должна стать необходимой частью работы каждого ученика.
Очевидно, что проверку усвоения материала нельзя ограничивать итоговым тематическим зачетом, полностью откладывать ее до конца темы. При использовании тематических зачетов в ходе изучения темы учителя систематически проверяют знания и умения учащихся в той или иной форме: устный опрос, проведение проверочных письменных работы т. д. При этом учитель специально предусматривает вопросы и задачи, которые позволяют ему следить, как учащиеся овладевают окончательными результатами обучения. Опытные учителя делают это уже в ходе текущих проверок. К зачету они подходят уже имея предварительную картину успеваемости каждого ученика. Это позволяет им управлять подготовкой учащихся к зачету.
Необходимой является работа с родителями. Им надо рассказать, в чем заключается особенность зачетной системы, разъяснить значение базовой математической подготовки для каждого выпускника школы. Родителям важно объяснить, что их поддержка стремления ребенка к сдаче зачетов играет большую роль в его школьных успехах [3].
5. Организация проведения зачета
Зачеты можно проводить по-разному. Это зависит от стиля работы учителя, его опыта, комплектности и состава класса. Опишем возможные варианты. Остановимся на практике организации тематических зачетов.
Тематический зачет рекомендуется проводить на уроке (в старших классах для этой цели могут быть выделены два урока). Проведение зачета, не нарушающего привычного хода учебного процесса, удобно, когда в запасе есть еще резерв времени для устранения возможных недостатков в обязательной подготовке учащихся. Поэтому зачет целесообразно проводить за один тАУ два урока до запланированного окончания изучения темы. Нужно отметить, что, хотя такая рекомендация кажется очевидной, к ней пришли не сразу. Многим учителям казалось возможным принимать зачеты после уроков, причем в самом конце изучения темы (а то и после ее изучения). И то и другое нарушало процесс учения в школе. Зачет вне урока не укладывался в ограниченное время, вел к перегрузке учеников и учителя. А откладывание зачета на конец этапа завершения темы чаще всего вело к нарушению планирования изучения последующих тем, так как его результаты требовали устранения пробелов, недостатков в знаниях и умениях учащихся и соответственно дополнительного учебного времени.
Зачет может проводиться в письменной или устной форме. Если он проводится письменно, то его организация напоминает обычную контрольную работу: ученик получает задание, выполняет его в отведенное время, сдает учителю, который проверяет работу во внеурочное время и затем раздает учащимся, анализируя с ними результаты выполнения. Отличие зачета от контрольной работы состоит лишь в содержании и необходимости по пересдачи. Поэтому на методике проведения такого зачета мы подробнее не останавливаемся.
При устной форме зачета учащийся, как на устном экзамене, получив задание, некоторое время готовится к ответу по нему. Ученик делает все необходимые записи, но в этих записях не требуется полное письменное оформление работы, как это принято и письменных контрольных работах. Например, при решении геометрической задачи ученик может сделать рисунок и провести необходимые вычисления; все доказательные рассуждения он будет проводить устно. Проверка работы учащихся проводится в ходе урока по мере выполнения ими контрольных заданий. При этом учитель имеет возможность по мере необходимости задать ученику вопросы, уточнить в ходе беседы его подготовку.
При смешанной форме зачета часть учащихся класса можно опросить устно, а остальным предложить выполнить задание письменно и сдать учителю на проверку.
Практика показала, что при любой форме проведения зачетов наиболее эффективна такая организация, когда ученик уже в ходе зачета или непосредственно после его сдачи узнает результат: успешно ли он справился с работой, какие задачи выполнил неверно и вынужден будет пересдавать. Поэтому заслуживает внимания опыт учителей, которые разработали методику проведения зачетов, позволяющую проводить проверку выполнения учеником обязательных заданий в процессе проведения зачетов.
В ходе такого зачета каждый ученик работает в индивидуальном темпе. Учитель, проходя по классу, или заглядываем и работу то одного, то другого учащегося, или ученики, выполнив задания обязательной части, по очереди подходят к учителю для проверки. Одновременно учитель либо отмечает в тетрадях учеников верное решение задачи знаком Вл+В», либо указывает на необходимость исправления неверного решения. Таким образом, если в решении хотя бы одной из задач обязательной части допущена ошибка, то учащемуся предоставляется право продолжить работу, т. е. самому найти ошибки и исправить их, а, получив одобрение учителя, приняться за решение задач дополнительной части. Для учителя наиболее трудная часть работы в течение урока тАУ контроль каждого ученика. Но при должной организации урока трудности значительно уменьшаются. Во-первых, учитель проверяет не каждое задание, а всю обязательную часть в целом. Поэтому первую треть урока он относительно свободен и уделяет внимание тем учащимся, которые недостаточно организованно начинают работу. Вторая треть урока тАУ это Влчас пикВ» для учителя. Но если он заранее позаботился посадить недалеко друг от друга тех ребят, которые обычно работают в быстром темпе, то в этот Влчас пикВ» ему не приходится много перемещаться по классу. Во-вторых, существенным элементом организации контроля являются предварительные записи в тетради учителя. Задачи всех вариантов записываются на одном листе. При этом крупно выделяются номера заданий и их ответы. Это позволяет не терять времени ни на поиск соответствующего номера, ни на решение заданий. Заметим, что последняя треть урока не требует большого напряжения. Учащиеся, получившие ВлзачетВ», углубляются в следующие задания, а остальные доделывают работу. Иногда слабому ученику учитель считает целесообразным дать задачу, аналогичную той, где была допущена ошибка, для подтверждения результатов контроля. Оценки тАЬ4тАЭ и тАЬ5тАЭ он может выставить и после урока, собрав тетради у тех, кто справился со всей работой.
Можно не требовать от учащихся полного письменного оформления решения задач. При решении задачи ученик может делать только необходимые ему записи. Все вспомогательные вычисления следует проводить здесь же; часть пояснений, которые ученик может сделать устно, он может опустить. Например, при решении задачи на составление уравнения ученик может сразу записать составленное уравнение или сделать минимальные пояснения (записать, какая величина в задаче обозначена буквой, а также выразить через эту букву необходимые величины). Минимальными записями можно ограничиться и при решении геометрических задач.
Для учета выполнения учащимся на зачете обязательных задач учитель ведёт специальную ведомость. В ней указываются номера задач (или характеристика содержания этих задач: деление натуральных чисел, нахождение процента числа и т. д.), выполнявшихся учеником, и отмечается знаком Вл+В» верное выполнение задания, знаком ВлтАУВ» тАУ зад
Вместе с этим смотрят:
WEB-дизайн: Flash технологии
РЖiрархiчна структура управлiння фiзичною культурою i спортом в Хмельницькiй областi у м. КамтАЩянець-Подiльському
РЖгрова дiяльнiсть в групi продовженого дня
РЖнновацiйнi методи навчання на уроках зарубiжноi лiтератури
РЖнтенсифiкацiя навчального процесу у вищiй школi