Математическая логика

Тема контрольной работы ВлМатематическая логикаВ».

БУЛЬ или БУЛ, а также БУУЛ, Джордж (1815-1864) тАУ английский математик, который считается основоположником математической логики.

Математическая логика тАУ это раздел математики, посвященный анализу методов рассуждений, при этом в первую очередь исследуются формы рассуждений, а не их содержание, т.е. исследуется формализация рассуждений.

Формализация рассуждений восходит к Аристотелю. Современный вид аристотелева (формальная) логика приобрела во второй половине XIX века в сочинении Джорджа Буля тАЬЗаконы мыслитАЭ.

Интенсивно математическая логика начала развиваться в 50-е годы XX века в связи с бурным развитием цифровой техники.

1. Элементы математической логика

Основными разделами математической логики являются исчисление высказываний и исчисление предикатов.

Высказывание тАУ есть предложение, которое может быть либо истинно, либо ложно.

Исчисление высказываний тАУ вступительный раздел математической логики, в котором рассматриваются логические операции над высказываниями.

Предикат тАУ логическая функция от п переменных, которая принимает значения истинности или ложности.

Исчисление предикатов тАУ раздел математической логики, объектом которого является дальнейшее изучение и обобщение исчисления высказываний.

Теория булевых алгебр (булевых функций) положена в основу точных методов анализа и синтеза в теории переключательных схем при проектировании компьютерных систем.

1.1 Основные понятия алгебры логики

Алгебра логики тАУ раздел математической логики, изучающий логические операции над высказываниями.

В алгебре логики интересуются лишь истинностным значением высказываний. Истинностные значения принято обозначать:

1 (истина) 0 (ложь).

Каждой логической операции соответствует функция, принимающая значения 1 или 0, аргументы которой также принимают значения 1 или 0.

Такие функции называются логическими или булевыми, или функциями алгебры логики (ФАЛ). При этом логическая (булева) переменная xможет принимать только два значения: .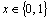

Таким образом, 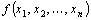Ва- логическая функция, у которой логи-ческие переменные 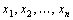Ваявляются высказываниями. Тогда сама логическая функция 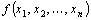Ваявляется сложным высказыванием.

В этом случае алгебру логики можно определить, как совокупность множества логических функций с заданными в нем всевозможными логическими операциями. Таким логическим операциям, как конъюнкция (читается И), дизъюнкция (ИЛИ), импликация, эквивалентность, отрицание (НЕ), соответствуют логические функции, для которых приняты обозначения 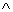(&, В·), 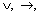~, тАУ (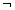), и имеет место таблица истинности:

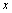
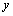
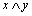
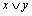
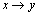
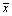
						x~y
0	0	0	0	1	1	1
0	1	0	1	1	1	0
1	0	0	1	0	0	0
1	1	1	1	1	0	Ва1

Это табличный способ задания ФАЛ. Наряду с ними применяется задание функций с помощью формул в языке, содержащем переменные x, y, тАж, z (возможно индексированные) и символы некоторых конкретных функций тАУ аналитический способ задания ФАЛ.

Наиболее употребительным является язык,содержащий логические символы 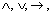Ва~, тАУ. Формулы этого языка определяются следующим образом:

1) все переменные есть формулы;

2) если Pи Q тАУ формулы, то 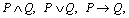P ~ Q, 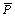Ва- фор-мулы.

Например, выражение 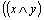~ 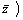- формула. Если переменным x, y, z придать значения из двоичного набора 0, 1 и провести вычисления в соответствии с операциями, указанными в формуле, то получим значение 0 или 1.

Говорят, что формула реализует функцию. Так формула 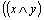~ 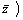реализует функцию h(x, y, z):

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Аксонометричнi проекцii