Методы минимизации логических функций
Содержание
Задание 1.Определить МДНФ логической функции устройства.
1.1 Составить таблицу соответствия (истинности) функции.
1.2 Перевести логическую функцию от табличной к аналитической форме в виде ДСНФ
1.3 Найти МДНФ различными методами.
1.3.1прямым (алгебраическим) преобразованием;
1.3.2методом Квайна;
1.3.3усовершенствованным методом Квайна (Квайна-Маккласки);
1.3.4методом карт Карно;
1.3.5методом неопределенных коэффициентов;
Задание 2. Составить алгоритм метода минимизации
2.1 Составить содержательный (словесный) алгоритм минимизации функции, разработать граф-схему алгоритма, разработать логическую схему алгоритма в нотации Ляпунова для метода Квайна.
2.2 Составить содержательный (словесный) алгоритм минимизации функции, разработать граф-схему алгоритма, разработать логическую схему алгоритма в нотации Ляпунова для метода минимального покрытия Петрика.
2.3 Разработать рабочие программы по алгоритмам.
Задание 3. Синтез схемы логического устройства.
3.1 Выполнить синтез схемы по ДСНФ и МДНФ в базисе Буля с использованием двухвходовых логических элементов и интегральных микросхем серии 155.
3.2 Функцию МДНФ в базисе Буля полученную в первом задании представить в базисах Шеффера и Пирса.
3.3 Обосновать выбор базиса по формулам МДНФ.
3.4 Реализовать в выбранном базисе логическую схему.
Задание 1.
1.1 Составить таблицу соответствия (истинности) функции.
Составим таблицу истинности для заданной функцииF(X1,X2,X3,X4).
№ | X1 | X2 | X3 | X4 | F(X1, X2, X3, X4) |
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 | 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 | 1 0 1 1 0 1 1 1 0 0 1 1 0 0 0 1 |
Матрицу ДСНФ получают путем удаления тех строк, где функция равна нулю. Для нашего случая получим:
| № | X1 | X2 | X3 | X4 |
0 2 3 5 6 7 10 11 15 | 0 0 0 0 0 0 1 1 1 | 0 0 0 1 1 1 0 0 1 | 0 1 1 0 1 1 1 1 1 | 0 0 1 1 0 1 0 1 1 |
1.2Перевести логическую функцию от табличной к аналитической форме в виде ДСНФ.
Переведем логическую функцию от табличной к аналитической форме в виде ДСНФ.
F(X1X2X3X4) = X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4
V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4.
1.3 Найти МДНФ различными методами.
1.3.1 Метод эквивалентных преобразований.
В основе метода минимизации булевых функций эквивалентными преобразованиями лежит последовательное использование законов булевой алгебры. Метод эквивалентных преобразований целесообразно использовать лишь для простых функций и для количества логических переменных не более 4-х. При большем числе переменных и сложной функции вероятность ошибок при преобразовании возрастает.
Проведем прямое алгебраическое преобразование, используя закон неполного склеивания.
F(X1X2X3X4) = X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V
V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 V X1X2X3X4 =
= (X1X2X3X4 V X1X2X3X4) V (X1X2X3X4 V X1X2X3X4)V(X1X2X3X4 V X1X2X3X4) V
V (X1X2X3X4 V X1X2X3X4) V (X1X2X3X4 V X1X2X3X4)V(X1X2X3X4 V X1X2X3X4) V
V (X1X2X3X4 V X1X2X3X4) V (X1X2X3X4 V X1X2X3X4)V(X1X2X3X4 V X1X2X3X4) V
V (X1X2X3X4 V X1X2X3X4) V (X1X2X3X4 V X1X2X3X4) =
= X1X2X4 V X1X2X3 V X1X3X4 V X2X3X4 V X1X3X4 V X2X3X4 V X1X2X4 V
V X1X2X3V X2X3X4 V X1X2X3 V X1X3X4 =
= (X1X2X3 V X1X2X3 V X1X3X4 V X1X3X4) V X1X2X4 V
V (X1X2X3 V X1X2X3 V X2X3X4 V X2X3X4) V X1X2X4 V
V (X1X3X4 V X1X3X4 V X2X3X4 V X2X3X4) =
= X1X3 V X2X3 V X3X4 V X1X2X4 V X1X2X4.
Дальнейшее преобразование невозможно. Полученную функцию можно немного упростить с помощью вынесения за скобки общих переменных.
1.3.2 Метод Квайна
При минимизации по методу Квайна предполагается, что минимизируемая логическая функция задана в виде ДСНФ. Здесь используется закон неполного склеивания. Минимизация проводится в два этапа: нахождение простых импликант, расстановка меток и определение существенных импликант (Q-матрица).
ДСНФ, ранг 4 |
1 2 3 4 5 6 7 8 9 | 0000 0010 0011 0101 0110 0111 1010 1011 1111 |
Наборы 3-го ранга |
1-2 2-3 2-5 2-7 3-6 3-8 4-6 5-6 6-9 7-8 8-9 | 00*0 001* 0*10 *010 0*11 *011 01*1 011* *111 101* 1*11 | 1 2 3 4 5 6 7 8 9 10 11 |
Наборы 2-го ранга |
2-8 2-10 3-5 4-6 5-11 6-9 | 0*1* *01* 0*1* *01* **11 **11 |
| | | |
Как видно из таблиц, при получении матрицы второго ранга первый и седьмой наборы третьего ранга не склеились ни с какими другими наборами. Их необходимо занести в конечную матрицу простых импликант. В матрице же второго ранга мы видим, что некоторые наборы одинаковые. Их необходимо вычеркнуть, так как дизъюнкция одинаковых наборов равна этой же дизъюнкции (это следует из закона повторения)
Простые импликанты |
1 2 3 4 5 | 0*1* *01* **11 00*0 01*1 |
Перенеся все выделенные строки в конечный массив, получим матрицу СДНФ. Алгебраическая запись СДНФ будет выглядеть следующим образом:
F(X1X2X3X4) = X1X3 V X2X3 V X3X4 V X1X2X4 V X1X2X4.
Эта же функция в нашем случае является и минимальной ДНФ.
1.3.3 Метод Квайна-Маккласки
В основу данного метода также положен закон неполного склеивания. Только в отличие от метода Квайна здесь производится гораздо меньше сравнений, так как, разбив исходную матрицу на несколько групп, мы сравниваем только те наборы, которые отличаются индексом на 1 или местоположением меток.
Распределим импликанты ДСНФ по индексам.
ДСНФ | Индекс i |
1 2 3 4 5 6 7 8 9 | 0000 0010 0011 0101 0110 0111 1010 1011 1111 | 0 1 2 2 2 3 2 3 4 |
| | |
Распределенные наборы 4-го ранга |
| i=0 | i=1 | i=2 | i=3 | i=4 |
| 0000 | 0010 | 0011 0101 0110 1010 | 0111 1011 | 1111 |
Сравнивая соседние группы и распределяя полученные наборы по положению символа тАШ*тАЩ получим:
Наборы 3-го ранга |
1 2 3 4 5 6 7 8 9 10 11 | 00*0 001* 0*10 *010 0*11 *011 01*1 011* *111 101* 1*11 |
Распределенные наборы 3-го ранга |
| 1 | 2 | 3 | 4 |
*010 *011 *111 | 0*10 0*11 1*11 | 00*0 01*1 | 001* 011* 101* |
Распределенные наборы 2-го ранга |
| 12 | 14 | 24 |
**11 | *01* | 0*1* |
Примечание. Во всех выше приведенных таблицах простые импликанты отмечены жирным шрифтом с подчеркиванием.
Анализируя, видим, что СДНФ примет следующий вид:
Простые импликанты |
1 2 3 4 5 | 0*1* *01* **11 00*0 01*1 |
Или в алгебраической форме:
F(X1X2X3X4) = X1X3 V X2X3 V X3X4 V X1X2X4 V X1X2X4.
1.3.4 Метод карт Карно.
Метод карт Карно тАУ это один из графических методов минимизации функции. Эти методы основаны на использовании особенности зрительного восприятия, так как с его помощью можно практически мгновенно распознать те или иные простые конфигурации.
Преимуществами метода карт Карно над другими методами являются:
А) простота отыскания склеивающихся компонент;
Б) простота выполнения самого склеивания;
В) нахождение всех минимальных форм функции.
Построим таблицу метода карт Карно.
| X1X2 | X1X2 | X1X2 | X1X2 |
X3X4 | ■ | | | |
X3X4 | | ■ | | |
X3X4 | ■ | ■ | ■ | ■ |
X3X4 | ■ | ■ | | ■ |
Теперь накроем совокупность всех квадратов с метками минимальным количеством правильных прямоугольников. Таких прямоугольников в нашем случае будет 5: три четырехклеточных и два двухклеточных. Этим прямоугольникам соответствуют следующие простые импликанты:
для первого тАУ X3X4;
для второго тАУ X1X3;
для третьего тАУ X2X3;
для четвертого тАУ X1X2X4;
для пятого тАУ X1X2X4;
Минимальная ДНФ будет выглядеть так:
F(X1X2X3X4) = X1X3 V X2X3 V X3X4 V X1X2X4 V X1X2X4.
Сравнивая метод карт Карно с другими методами минимизации функции можно сделать вывод, что первый больше всего подходит для ручного исполнения. Время ручной работы значительно сокращается (за счет наглядного представления склеивающихся импликант). Программная реализация данного метода имеет свои сложности. Так, очень сложно будет реализовать оптимальный выбор правильных прямоугольников, особенно для большого числа аргументов.
1.3.5 Метод неопределенных коэффициентов
Этот метод может быть использован для любого числа аргументов. Но так как этот метод достаточно громоздок, то применяется только в тех случаях, когда число аргументов не более 5-6.
В методе неопределенных коэффициентов используются законы универсального и нулевого множеств и законы повторения. В начале все коэффициенты неопределенны (отсюда и название метода).
Построим матрицу неопределенных коэффициентов для четырех аргументов. В этом случае мы будем иметь систему из 16-ти уравнений.
Система приведена на следующей странице.
Приравняем все коэффициенты 0 в тех строках, которым соответствует 0 в векторе столбце. Затем приравняем 0 соответствующие коэффициенты в других строках. После этих преобразований система примет следующий вид:
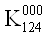 ВаV
ВаV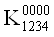 Ва= 1
Ва= 1
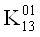 V
V  ВаV
ВаV 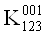 V
V 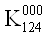 ВаV
ВаV 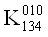 ВаV
ВаV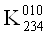 V
V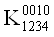 Ва= 1
Ва= 1
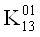 V
V  ВаV
ВаV  ВаV
ВаV 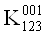 ВаV
ВаV 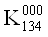 ВаV
ВаV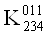 V
V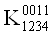 Ва= 1
Ва= 1
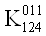 ВаV
ВаV 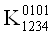 Ва= 1
Ва= 1
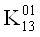 V
V 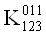 ВаV
ВаV 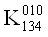 V
V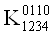 Ва= 1
Ва= 1
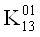 ВаV
ВаV  ВаV
ВаV 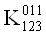 V
V 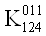 ВаV
ВаV 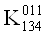 ВаV
ВаV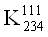 V
V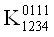 Ва= 1
Ва= 1
 ВаV
ВаV 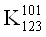 ВаV
ВаV 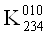 V
V 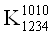 Ва= 1
Ва= 1
 ВаV
ВаV  ВаV
ВаV 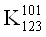 ВаV
ВаV 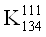 ВаV
ВаV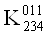 V
V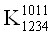 Ва= 1
Ва= 1
 ВаV
ВаV 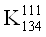 ВаV
ВаV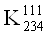 V
V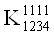 Ва= 1
Ва= 1
Теперь в каждой строке необходимо выбрать коэффициент минимального ранга и приравнять его единице, а остальные коэффициенты тАУ 0. После этого вычеркиваем одинаковые строки, оставляя при этом одну из них (те строки, у которых все коэффициенты равны 0, также вычеркиваются).
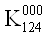 Ва= 1
Ва= 1
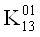 = 1
= 1
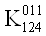 = 1
= 1
 = 1
= 1
 = 1
= 1
Запишем теперь конъюнкции, соответствующие коэффициентам, равным единицам. Мы получим минимальную ДНФ.
F(X1X2X3X4) = X1X3 V X2X3 V X3X4 V X1X2X4 V X1X2X4.
Итак, мы получили несколькими способами минимальную ДНФ, Во всех случаях она получилась одинаковой, то есть любой из описанных методов может быть использован для минимизации функции. Однако эти методы существенно отличаются друг от друга как по принципу нахождения МДНФ, так и по времени исполнения. Для ручных расчетов очень удобен метод карт Карно. Он нагляден, не требует рутинных операций, а выбрать оптимальное расположение правильных прямоугольников не составляет большого труда. В то время как машинная реализация данного метода осложняется необходимостью нахождения оптимального расположения прямоугольников. Естественно применение других методов (метод Квайна, метод Квайна-Маккласки, метод неопределенных коэффициентов) для ручных расчетов нецелесообразно. Они больше подойдут для машинной реализации, так как содержат большое число повторяющихся простых операций.
Задание 2.
2.1 Схема алгоритма для метода Квайна
1. Начало.
2. Ввести матрицу ДСНФ исходной функции.
3. Проверить на склеиваемость i-ю (i=1,m-1: где m тАУ количество строк в ДСНФ) и j-ую (j=i+1, m) строки. Если строки склеиваются, то перейти к пункту 6, в противном случае перейти к пункту 5.
4. Формировать массив простых импликант, предварительно пометив символом тАШ*тАЩ ту переменную, по которой данные строки склеиваются.
5. Перейти к пункту 2.
6. Строку, которая не склеилась ни с одной другой строкой записать в конечный массив.
7. Перейти к пункту 2.
8. Вывод полученной матрицы.
9. Конец.
Логическая схема алгоритма в нотации Ляпунова
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 1ВаВаВаВаВаВаВаВа 1Ва
VHV1Z1ВнV2¯V3V4VK
VH тАУ начало.
V1 тАУ ввести матрицу ДСНФ исходной функции.
V2 тАУ формировать массив простых импликант, предварительно пометив символом тАШ*тАЩ ту переменную, по которой данные строки склеиваются.
V3 тАУ строку, которая не склеилась ни с одной другой строкой записать в конечный массив.
V4 тАУ вывод полученной матрицы.
Z1 тАУ если строки склеиваются, то перейти к пункту 3, в противном случае перейти к пункту 5.
VK тАУ конец.
Граф-схема алгоритма.

Описаниемашинныхпроцедур
Procedure Stuck(S1, S2: Diz; IndexS1, IndexS2 : byte);
Данная процедура склеивает два, передаваемых ей дизъюнкта. Дизъюнкты задаются в параметрах S1, S2. Индексы IndexS1, IndexS2 определяют индексы этих дизъюнктов в главном рабочем массиве . Алгоритм работы процедуры следующий: сначала ищется количество склеивающихся символов. Если их 0, то они одинаковые, и в конечный массив записывается только один из них. Если 1, то определяется местоположение символа, по которому данные две дизъюнкции склеиваются, и заменяем этот символ на тАШ*тАЩ. Все полученные результаты заносятся в массив REZ.
Все остальные функции и процедуры программы связаны с действиями над массивами, то есть не имеют непосредственного отношения к данному методу нахождения МДНФ. Поэтому нет смысла их описывать.
2.2 Схема алгоритма для метода Петрика
1. Начало.
2. Ввести матрицу ДСНФ исходной функции и простые импликанты, полученные в методе Квайна.
3. Составить таблицу меток.
4. По таблице меток построить конъюнкцию дизъюнкций, каждая из которых есть совокупность тех импликант, которые в данном столбце имеют метки.
5. Произвести раскрытие скобок в полученном выражении с учетом законов поглощения.
6. Выбрать одну из полученных конъюнкций и представить ее как совокупность соответсвующих простых импликант.
7. Если выбранная комбинация не является минимальной, то перейти к пункту 6, в противном случае перейти к пункту 8.
8. Формировать МДНФ.
9. Вывод полученной матрицы.
10. Конец.
Логическая схема алгоритма в нотации Ляпунова.
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 1ВаВаВаВаВаВаВаВаВаВаВаВа 1Ва
VHV1V2V3V4¯V5Z1ВнV6V7VK
VH тАУ начало.
V1 тАУ ввести матрицу ДСНФ исходной функции и простые импликанты, полученные в методе Квайна.
V2 тАУ составить таблицу меток.
V3 тАУ по таблице меток построить конъюнкцию дизъюнкций, каждая из которых есть совокупность тех импликант, которые в данном столбце имеют метки.
V4 тАУ произвести раскрытие скобок в полученном выражении с учетом законов поглощения.
V5 тАУ выбрать одну из полученных конъюнкций и представить ее как совокупность соответсвующих простых импликант.
Z1 тАУ если выбранная комбинация не является минимальной, то перейти к пункту 6, в противном случае перейти к пункту 8.
V6 тАУ формировать МДНФ.
V7 тАУ вывод полученной матрицы.
VK тАУ конец.
Граф-схема алгоритма.
Описание машинных процедур
Procedure FormMatrix;
Данная процедура формирует матрицу меток путем попарного анализа дизъюнктов из ДСНФ и матрицы простых импликант. Если стравнение прошло успешно, то соответствующему элементу матрицы меток присваивается значение 1, в противном случае тАУ значение 0.
Function Pokritie(var S: string16): boolean;
Данная функция проверяет, является ли данная комбинация простых импликант полной, то есть накрывает ли она все дизъюнкты матрицы ДСНФ. Это сравнение происходит следующим образом: вводится новый массив тАУ массив соостветсвия столбцам. Каждому элементу нового массива сначала присваивается значение 0. Далее, пробегая все заданные строки матрицы,определяем в каких столбцах стоит 1 и в новом массиве ставим на соответсвующее место 1. Таким образом, если в векторе есть нули, значит данная комбинация дизъюнктов не накрывает полностью все столбцы матрицы. В этом случае функция возвращает значние False, в противном случае функция возвращает значение True.
Задание 3. Синтез схемы логического устройства.
1. Представление МДНФ в базисе Буля. В базисе Буля используется 3 логические схемы: НЕ, ИЛИ, И. Вот их графическое изображение: