Векторная алгебра
Проекция вектора на ось:
Проекцией точки на прямую называется основание перпендикуляра, опущенного из этой точки на прямую. Проекция АВ на х это число |AтАЩBтАЩ| взятое со знаком +, если угол острый и со знаком тАУ если угол тупой.
, 
.
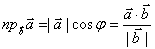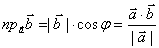
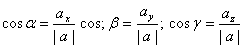Скалярное произведение векторов
. 
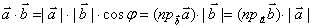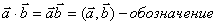
Признак перпендикулярности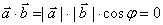 
.
Векторное произведение векторов
; 
; 
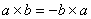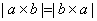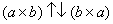
Объем пирамиды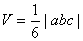 
; 
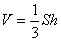
Смешанное произведение векторов
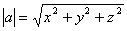
Если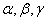 
Ва- углы, которые составляет вектор а с координатными осями, то 
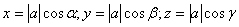, откуда следует
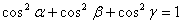
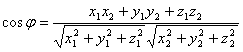
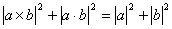
Условие коллинеарности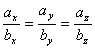 
ab=0 тАУ перпендикулярность
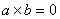Ва- коллинеарность
abc=0 тАУ компланарность
Аналитическая геометрия
Плоскость в пространстве
Нормаль и точка привязки однозначно определяют положение плоскости в пространстве.
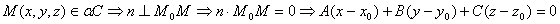Ва-
каноническое уравнение (1)
Общее уравнение плоскости
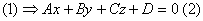, где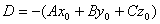 
,
где А, В, С тАУ координаты нормали, D тАУ свободный член, x,y,z тАУ текущий координаты.
Уравнение плоскости, проходящий через точку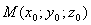 
Ваперпендикулярно вектору N=(A;B;C), имеет вид
Уравнение плоскости, проходящей через три заданные точки записывают в виде
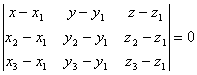
Уравнение плоскости в отрезках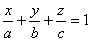 
Нормальное уравнение плоскости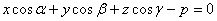 
, где p тАУ расстояние от начала координат.
Нормирующий множитель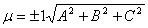 
Расстояние от точки до плоскости
Угол между плоскостями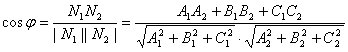 
Условия параллельности и перпендикулярности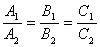 
; 
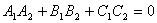
Уравнение пучка плоскостей: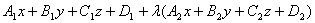 
Прямые линии в пространстве.
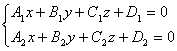-уравнение прямой
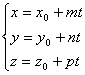Ва- параметрическое уравнение прямой.
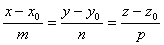Ва- каноническое уравнение прямой.
Уравнения прямой, проходящей через 2 заданные точки
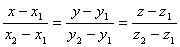
Угол между 2 прямыми
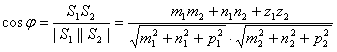
Взаимное расположение 2 прямых.
1. 
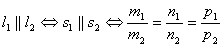Ва(могут лежать и на одной прямой)
2. 
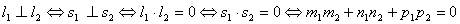Ва(могут скрещиваться)
3. 
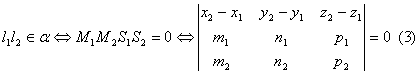. Если (3) 
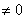, то скрещиваются.
Взаимное расположение прямой и плоскости
1. 
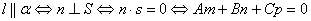
2. 
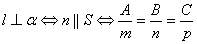
3. Угол между прямой и плоскостью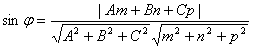 
4. 
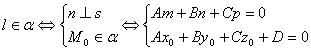
Аналитическая геометрия на плоскости.
Прямоугольная декартова система координат на плоскости
Расстояние между 2 точками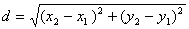 
.
Если заданы точки А и В и точка С делит отрезок АВ в отношении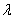 
, т.е. 
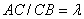, то 
.
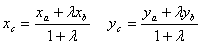Уравнение прямой на плоскости
Ax+By+C=0;
Уравнение прямой в отрезках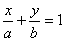 
.
Уравнение прямой, проходящей через 2 заданные точки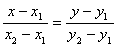 
.
Уравнение прямой, проходящей через точку, под заданным углом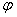 
к оси Ох (
): 
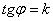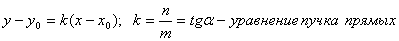
Расстояние от точки до прямой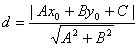 
1. 
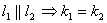
2. 
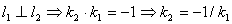
3. 
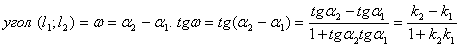
Окружность
Уравнение окружности с центром в M(a;b) радиусом R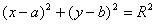 
Уравнение окружности с центром в начале координат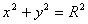 
Эллипс
Эллипс тАУ геометрическое место точек, для которых сумма расстояний до двух заданных точек плоскости (фокусов эллипса) есть величина постоянная,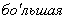 
, чем расстояние между фокусами.
Обозначим M(x;y) тАУ произвольная точка эллипса, 2с тАУ расстояние между фокусами F1 и F2; 2а тАУ сумма расстояний от точки М до F1 и F2 (a тАУ большая полуось эллипса).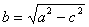 
Ва- малая полуось эллипса. 
.
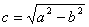Тогда каноническое уравнение эллипса имеет вид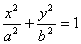 
. 
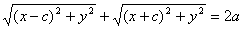
Число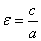 
Ваназывается эксцентриситетом эллипса и характеризует сплюснутость эллипса относительно осей 
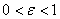. Если 
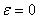, то получается окружность. a=b.
Гипербола
Гипербола тАУ геометрическое место точек, разность расстояний которых от двух заданных точек (фокусов) есть постоянная величина, меньшая, чем расстояние между фокусами.
Если M (x;y) тАУ точка гиперболы; F1, F2 тАУ фокусы, 2с тАУ расстояние между фокусами, 2а тАУ разность расстояний от точки М (х;y) до фокусов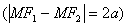 
, где а тАУ действительная полуось гиперболы. 
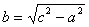Ва- мнимая полуось гиперболы.
Каноническое уравнение гиперболы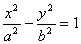 
.
Гипербола пересекает ось Ох в точках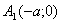 
Ваи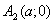 
, с осью Оу пересечений нет.
Гипербола имеет две асимптоты, уравнения которых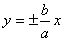 
.
Эксцентриситет гиперболы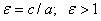 
.
Парабола
Парабола тАУ геометрическое место точек, равноудаленных от заданной точки F тАУ фокуса и заданной прямой тАУ директрисы параболы. Если ось абсцисс совпадает с перпендикуляром, опущенным из фокуса на директрису, а начало координат делит этот перпендикуляр пополам, то каноническое уравнение имеет вид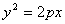 
.
Эксцентриситет параболы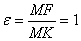 
Ва- отношение расстояния от точки параболы до директрисы к расстоянию от этой точки до фокуса.
Общее уравнение второго порядка
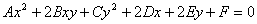Ва- общее уравнение кривой второго порядка
Параллельный перенос: 
.
Поворот осей: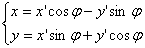 
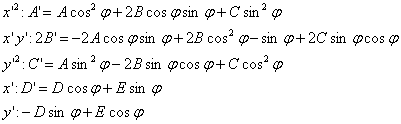
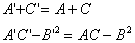Ва- инварианты. 
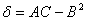Ва- дискриминант
Если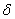 
>0, то уравнение эллиптического вида
Если 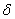<0, то уравнение гиперболического типа
Если 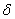=0, то уравнение параболического типа
Выбираем угол так, чтобы BтАЩ=0, тогда
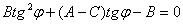
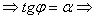
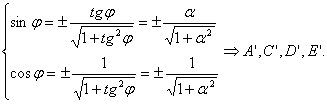
(1) 
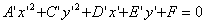Ва(B=0)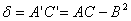 
1. 
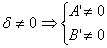. Осуществляем параллельный перенос для уничтожения членов 
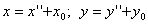.(**) ** подставляем в
(1)
+ 
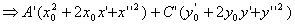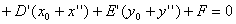
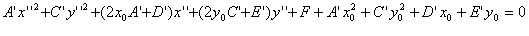
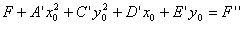
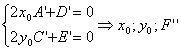
(2)
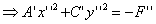(3)
а)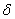>0 тАУ эллиптический вид
A`C`>0 (одного знака)
Если F``>0, то пустое множество
Если F``=0, то одна точка (x``=0, y``=0)
Если F``<0, то получим эллипс в ви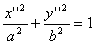де 
, где 
б) 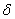<0 (гиперболический вид) AтАЩCтАЩ<0 (разные знаки). Пусть AтАЩ>0
A`=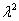
, 
, 
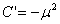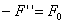, тогда 
.
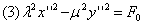Если F0=0, то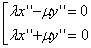 
, получаем пару пересекающихся прямых.
Если F0>0, то 
Ва(гипербола)
Если F0<0, то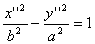 
Ва(гипербола, где оси поменялись местами)
в)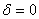
Ва(параболический тип) A`C`=0
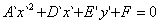Ва(5)
а) D`=E`=0, пусть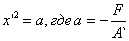 
б)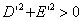 
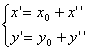
** в (5)
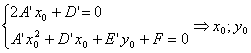
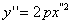, где 2р=
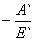, если p>0, то парабола 
.
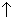Теория пределов
Число а называется пределом последовательности xn для любого (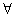
) сколь угодно малого положительного числа 
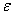Ванайдется номер, зависящий от 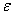, начиная с которого все члены последовательности отличаются от а меньше, чем на .
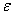Предел последовательности
Под числовой последовательностью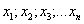
понимают функцию 
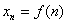, заданную на множестве натуральных чисел 
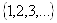т.е. функцию натурального аргумента.
Число a называется пределом последовательности xn(x=1,2,тАж):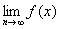 
=а, если для любого сколь угодно малого 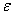>0, существует такое число N=N(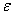), что для всех натуральных n>N выполняется неравенство 
.
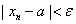1) , 
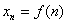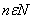Ва- натуральное число. Если xn=a, то (a, a, a, a) тАУ стационарная последовательность.
2) 
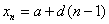, где a, d тАУ const, тогда (a, a+d, a+2d,тАжa+(n-1)d)
xn+1=xn+d тАУ рекуррентная формула.
3) Числа Фибоначчи. (1,1, 2, 3, 5, 8, 13, 21,тАж), где x1, x2 =1 и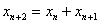 
.
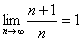Ва(*);
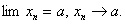
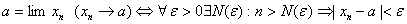
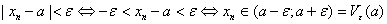Ва- эпсилон тАУ окрестность числа а.
1. 
. 
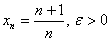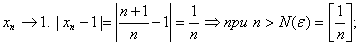
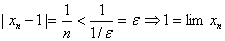
2. 
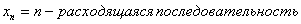
Основные теоремы пределах
1. О единственном пределе. Последовательность имеет не более 1 предела.
2. Предельный переход в неравенстве.
3. О трех последовательностях. О сжатой последовательности.
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Аксонометричнi проекцii