Орграфы, теория и применение

Актуальность темы.Теория графов предоставляет эффективные средства формализации задач из самых различных областей: экономики, физики, химии, планово-производственной практики, управления производством, сетевого и календарного планирования, информационных систем, и многих других. Одним из таких средств является ориентированный граф. Существует большое количество задач, решаемых на орграфах. Чаще всего рассматриваются задачи о достижимости (т.е. о существовании пути, связывающем две заданные вершины), о нахождении путей, обладающих какой-либо экстремальной характеристикой (например, кратчайший, или наиболее надежный путь), о случайных блужданиях, потоковая задача. Все они хорошо изучены и разработаны эффективные алгоритмы их решения. При этом предполагается, что все пути на графе являются допустимыми, т.е. не накладывается никаких ограничений на достижимость.

Наиболее известные работы в этой области принадлежат Кристофидесу Н., Басакеру Р.Д., Харари Ф., Бержу К., Дейкстре Э., Флойду Р., Замбицкому Д.К., Оре О., Саати Т., Фалкерсону Д.Р., Форду Л.Р.

В отличие от классического подхода, Басанговой Е.О. и Ерусалимским Я.М. было введено понятие ориентированных графов с нестандартной достижимостью, т.е. орграфов, в которых на допустимые пути накладываются какие-либо ограничения. В обычном ориентированном графе, для того чтобы одна вершина была достижима из другой, необходимо существование пути, связывающего две эти вершины. В случае же орграфов с нестандартной достижимостью требуется, кроме того, чтобы этот путь удовлетворял некоторому условию (ограничению). Понятно, что в этом случае классические алгоритмы решения задач на графах непосредственно неприменимы.

В работах Ерусалимского Я.М., Басанговой Е.О., Логвинова С.Ю., Скороходова В.А., Петросяна А.Г. описаны различные виды ограничений на достижимость. Так, Ерусалимским Я.М. и Басанговой Е.О. рассмотрено несколько видов достижимости на частично-ориентированных графах, на которых присутствуют ориентированные и неориентированные ребра. Введено понятие смешанной цепи, на дуги и звенья которой накладываются различные условия, в зависимости от вида ограничений. Например, рассмотрены случаи, когда в смешанной цепи два неориентированных ребра не могут следовать непосредственно друг за другом, или дуги и звенья строго чередуются.

В работах Скороходова В.А. рассмотрены орграфы с накоплением неубывающей магнитности 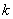Ва- го уровня. На таких графах допустимым является магнитно-накопительный путь порядка 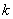Вас неубывающей магнитностью, т.е. такой путь, что если на 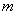Ва- м шаге величина накопленной магнитности не меньше 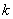Ваи среди выходящих дуг есть хотя бы одна магнитная, то 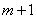Ва- я дуга пути должна быть магнитной. Другой вид достижимости тАУ вентильно-накопительная. В этом случае множество дуг графа представляется в виде 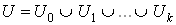. В допустимом пути прохождение по дуге множества 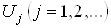Ваделает доступными для прохождения дуги множества 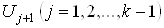. Также рассмотрены условия накопления - исчезания и возрастания-убывания магнитности, вентильная достижимость с возрастанием-убыванием доступа и энергии на пути, механическая достижимость.

Петросяном А.Г. определена барьерная достижимость, при которой множество дуг разбивается на три попарно непересекающихся подмножества: дуг, увеличивающих барьерный показатель, дуг барьерного перехода и нейтральных дуг. С каждым отрезком пути связана числовая характеристика тАУ барьерный показатель частицы. Путь допускает барьерный переход уровня 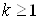, если к некоторому шагу он накопил величину барьерного показателя, не меньшую 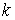. Еще один вид ограничений тАУ биполярная магнитность. В этом случае определяется величина накопления биполярной магнитности. Путь считается допустимым, если он удовлетворяет условию биполярной магнитности уровня .

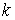Общим подходом к решению задач на орграфах с ограничениями на достижимость является построение вспомогательного графа, имеющего большее количество вершин, и обладающего следующим свойством: допустимому пути на исходном графе с ограничениями соответствует некоторый путь на вспомогательном графе, а недопустимому пути не соответствует ни один путь. Алгоритм построения такого графа зависит от вида вводимых ограничений. На вспомогательном графе, таким образом, все пути являются допустимыми, а дуги тАУ равноправными, и его можно рассматривать как обычный ориентированный граф. Для графов с нестандартными достижимостями описанных видов рассмотрены классические задачи о кратчайшем пути из вершины в вершину, о максимальном потоке в сети с нестандартной достижимостью и о случайных блужданиях на таких графах. Наибольшую сложность вызывают две последние задачи, так как при построении вспомогательного графа увеличивается не только количество вершин, но и количество дуг. При этом необходимо правильно распорядится весами дуг, по которым строится несколько дуг на вспомогательном графе. Серьезного осмысления каждый раз требует и перенос соответствующего результата с вспомогательного графа на основной граф.

Цели и задачи работы.Цель состоит в изучении графов с нестандартными достижимостями, разработке алгоритмов решения задач на таких графах, описании нового класса динамических графов, программной реализации полученных алгоритмов.

Глава 1. Граф. Общее представление

В математической теории графов и информатике граф тАФ это совокупность объектов со связями между ними.

Объекты представляются как вершины, или узлы графа, а связи тАФ как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами.

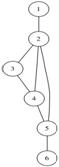
Неориентированный граф с шестью вершинами и семью рёбрами

Граф или неориентированный граф G тАФ это упорядоченная пара G: = (V,E), для которой выполнены следующие условия:

V это множество вершин или узлов, E это множество пар (в случае неориентированного графа тАФ неупорядоченных) вершин, называемых рёбрами. V (а значит и E) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становятся ложными в случае бесконечных множеств.

Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | тАФ порядком, число рёбер | E | тАФ размером графа.

Вершины u и v называются концевыми вершинами (или просто концами) ребра e = {u,v}. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Ребро называется петлёй, если его концы совпадают, то есть e = {v,v}.

Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Ориентированный граф (сокращённо орграф) G тАФ это упорядоченная пара G: = (V,A), для которой выполнены следующие условия:

V это множество вершин или узлов,

A это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Дуга тАФ это упорядоченная пара вершин (v, w), где вершину v называют началом, а w тАФ концом дуги. Можно сказать, что дуга v w ведёт от вершины v к вершине w.

Формально, орграф D=(V, E) есть множество E упорядоченных пар вершин .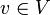

Дуга {u, v} инцидентна вершинам u и v. При этом говорят, что u тАФ начальная вершина дуги, а v тАФ конечная вершина.

Орграф, полученный из простого графа (Простой граф тАФ граф, в котором нет кратных рёбер и петель.) ориентацией ребер называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.

Направленный полный граф называется турниром. Полный граф тАФ простой граф, в котором каждая пара различных вершин смежна. Полный граф с n вершинами имеет n(n − 1) / 2 рёбер и обозначается Kn. Является регулярным графом степени n − 1.

Связность

Маршрутом в орграфе называют чередующуюся последовательность вершин и дуг, вида v0{v0,v1}v1{v1,v2}v2тАжvn (вершины могут повторяться). Длина маршрута тАФ количество дуг в нем.

Путь есть маршрут в орграфе без повторяющихся дуг, простой путь тАФ без повторяющихся вершин. Если существует путь из одной вершины в другую, то вторая вершина достижима из первой.

Контур есть замкнутый путь.

Для полумаршрута снимается ограничение на направление дуг, аналогично определяются полупуть и полуконтур.

Орграф сильно связный, или просто сильный если все его вершины взаимно достижимы; односторонне связный, или просто односторонний если для любых двух вершин, по крайней мере одна достижима из другой; слабо связный, или просто слабый, если при игнорировании направления дуг получается связный (мульти)граф;

Максимальный сильный подграф (Подграф исходного графа тАФ граф, содержащий некое подмножество вершин данного графа и все рёбра, инцидентные данному подмножеству. (ср. Суграф-частичный граф исходного графа тАФ граф, содержащий все вершины исходного графа и подмножество его рёбер)) называется сильной компонентой; (Орграф называется сильно связным (strongly connected), если любые две его вершины сильно связаны. Две вершины s и t любого графа сильно связаны, если существует ориентированный путь из s в t и ориентированный путь из t в s. Сильно связными компонентами орграфа называются его максимально сильно связные подграфы). Односторонняя компонента и слабая компонента определяются аналогично.

Конденсацией орграфа D называют орграф D*, вершинами которого служат сильные компоненты D, а дуга в D* показывает наличие хотя бы одной дуги между вершинами, входящими в соответствующие компоненты.

Дополнительные определения

Направленный ациклический граф или гамак есть бесконтурный орграф. (Направленный ациклический граф тАФ случай направленного графа, в котором отсутствуют направленные циклы, то есть пути, начинающиеся и кончающиеся в одной и той же вершине. Направленный ациклический граф является обобщением дерева (точнее, их объединения тАФ леса)).

Ориентированный граф, полученный из заданного сменой направления ребер на противоположное, называется обратным.

Изображение и свойства всех орграфов с тремя узлами. Легенда: С тАУ слабый, ОС тАУ односторонний, СС тАУ сильный, Н тАУ является направленным графом, Г тАУ является гамаком, Т тАУ является турниром.

0 дуг	1 дуга	2 дуги	3 дуги	4 дуги	5 дуг	6 дуг
пустой, Н, Г	Н, Г		ОС	CC	CC	полный, CC
		ОС, Н, Г	CC, Н, Т	CC
		C, Н, Г	ОС, Н, Г, Т	ОС
		C, Н, Г	ОС	ОС