Вычислительная математика
Исследование различных явлений или процессов математическими методами осуществляется с помощью математической модели. Математическая модель представляет собой формализованное описание на языке математики исследуемого объекта. Таким формализованным описанием может быть система линейных, нелинейных или дифференциальных уравнений, система неравенств, определенный интеграл, многочлен с неизвестными коэффициентами и т. д. Математическая модель должна охватывать важнейшие характеристики исследуемого объекта и отражать связи между ними.
После того, как математическая модель составлена, переходят к постановке вычислительной задачи. При этом устанавливают, какие характеристики математической модели являются исходными (входными) данными, какие тАУ параметрами модели, а какие тАУ выходными данными. Проводится анализ полученной задачи с точки зрения существования и единственности решения.
На следующем этапе выбирается метод решения задачи. Во многих конкретных случаях найти решение задачи в явном виде не представляется возможным, так как оно не выражается через элементарные функции. Такие задачи можно решить лишь приближенно. Под вычислительными (численными) методами подразумеваются приближенные процедуры, позволяющие получать решение в виде конкретных числовых значений. Вычислительные методы, как правило, реализуются на ЭВМ. Для решения одной и той же задачи могут быть использованы различные вычислительные методы, поэтому нужно уметь оценивать качество различных методов и эффективность их применения для данной задачи.
Затем для реализации выбранного вычислительного метода составляется алгоритм и программа для ЭВМ. Современному инженеру важно уметь преобразовать задачу к виду, удобному для реализации на ЭВМ и построить алгоритм решения такой задачи.
В настоящее время на рынке программного обеспечения широко представлены как пакеты, реализующие наиболее общие методы решения широкого круга задач (например, Maple, Mathcad, MatLAB), так и пакеты, реализующие методыВа решения специальных задач (например, задач газовой динамики).
Результаты расчета анализируются и интерпретируются. При необходимости корректируются параметры метода, а иногда математическая модель, и начинается новый цикл решения задачи.
Тема 1. Решение задач вычислительными методами.
Основные понятия
1.1 Погрешность
Существуют четыре источника погрешностей, возникающих в результате численного решения задачи.
1. Математическая модель. Погрешность математической модели связана с ее приближенным описанием реального объекта. Например, если при моделировании экономической системы не учитывать инфляции, а считать цены постоянными, трудно рассчитывать на достоверность результатов. Погрешность математической модели называется неустранимой. Будем в дальнейшем предполагать, что математическая модель фиксирована и ее погрешность учитывать не будем.
2. Исходные данные. Исходные данные, как правило, содержат погрешности, так как они либо неточно измерены, либо являются результатом решения некоторых вспомогательных задач. Например, масса снаряда, производительность оборудования, предполагаемая цена товара и др. Во многих физических и технических задачах погрешность измерений составляет 1 тАУ 10%. Погрешность исходных данных так же, как и погрешность математической модели, считается неустранимой и в дальнейшем учитываться не будет.
3. Метод вычислений. Применяемые для решения задачи методы как правило являются приближенными. Например, заменяют интеграл суммой, функцию тАУ многочленом, производную тАУ разностью и т. д. Погрешность метода необходимо определять для конкретного метода. Обычно ее можно оценить и проконтролировать. Следует выбирать погрешность метода так, чтобы она была не более, чем на порядок меньше неустранимой погрешности. Большая погрешность снижает точность решения, а меньшая требует значительного увеличения объема вычислений.
4. Округление в вычислениях. Погрешность округления возникает из-за того, что вычисления производятся с конечным числом значащих цифр (для ЭВМ это 10 тАУ 12 знаков). Округление производят по следующему правилу: если в старшем из отбрасываемых разрядов стоит цифра меньше пяти, то содержимое сохраняемых разрядов не изменяется; в противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа. При решении больших задач производятся миллиарды вычислений, но так как погрешности имеют разные знаки, то они частично взаимокомпенсируются.
Различают абсолютную и относительную погрешности. Пусть а тАУ точное, вообще говоря неизвестное числовое значение некоторой величины, а а* - известное приближенное значение этой величины, тогда величину
D(а*) = | аВа тАУВа а*|
называют абсолютной погрешностью числа а*, а величину
d(а*) = 
тАУ его относительной погрешностью.
При сложении и вычитании складываются абсолютные погрешности, а при делении и умножении тАУ относительные погрешности.
1.2 Корректность
Определим вначале понятие устойчивости решения.
Решение задачи y* называется устойчивым по исходным данным x*, если оно зависит от исходных данных непрерывным образом. Это означает, что малому изменению исходных данных соответствует малое изменение решения. Строго говоря, для любого e > 0 существует d = d(e) > 0 такое, что всякому исходному данному x*, удовлетворяющему условию |xВа - x*| < d, соответствует приближенное решение y*, для которого |y тАУ y*| < e.
Говорят, что задача поставлена корректно, если выполнены следующие три условия:
1. Решение существует при любых допустимых исходных данных.
2. Это решение единственно.
3. Это решение устойчиво по отношению к малым изменениям исходных данных.
Если хотя бы одно из этих условий не выполнено, задача называется некорректной.
Пример 1.1.
Покажем, что задача вычисления определенного интегралаВа I = 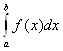 корректна. Пусть f*(x) тАУ приближенно заданная функция и I* =
корректна. Пусть f*(x) тАУ приближенно заданная функция и I* = 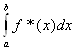 . Очевидно, приближенное решение I* существует и единственно. Определим абсолютную погрешность f* с помощью равенстваВа D(f*) =
. Очевидно, приближенное решение I* существует и единственно. Определим абсолютную погрешность f* с помощью равенстваВа D(f*) = 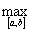 |f(x) тАУ f*(x)|. Так как
|f(x) тАУ f*(x)|. Так как
D(I) = |I тАУ I*| = | | £Ва (b тАУ a)D(f*),
| £Ва (b тАУ a)D(f*),
то для любого e > 0 неравенство D(I) < eВабудет выполнено, если будет выполнено условие D(f*) < d, где d= e /(b тАУ a).
Таким образом, решение I* устойчиво. Все три условия корректности задачи выполнены.
Пример 1.2.
Покажем, что задача вычисления производной u(x) = f '(x) приближенно заданной функции некорректна.
Пусть f*(x) тАУ приближенно заданная на отрезке [a, ] непрерывно дифференцируемаяВа функция и u*(x) = (f*(x))'. Определим абсолютные погрешности следующим образом: D(f*) = 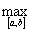 |f(x) тАУ f*(x)|, D(u*) =
|f(x) тАУ f*(x)|, D(u*) = 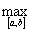 |u(x) тАУ u*(x)|.
|u(x) тАУ u*(x)|.
Возьмем, например, f*(x) = f(x) + a sin(x/a2), где 0 < a < 1. Тогда, u*(x) = u(x) + a-1cos(x/a2), D(u*) = a-1, т. е. погрешность задания функции равна a, а погрешность производной равна a-1. Таким образом, сколь угодно малой погрешности задания функции f может отвечать сколь угодно большая погрешность производной f '.
1.3 Вычислительные методы
Под вычислительными методами будем понимать методы, которые используются в вычислительной математике для преобразования задач к виду, удобному для реализации на ЭВМ. Подробнее с различными классами вычислительных методов можно познакомиться, например, в [1]. Мы же рассмотрим два класса методов, используемых в нашем курсе.
1. Прямые методы. Метод решения задачи называется прямым, если он позволяет получить решение после выполнения конечного числа элементарных операций. Наименование элементарной операции здесь условно. Это может быть, например, вычисление интеграла, решение системы уравнений, вычисление значений функции и т. д. Важно то, что ее сложность существенно меньше, чем сложность основной задачи. Иногда прямые методы называют точными, имея в виду, что при отсутствии ошибок в исходных данных и при выполнении элементарных операций результат будет точным. Однако, при реализации метода на ЭВМ неизбежны ошибки округления и, как следствие, наличие вычислительной погрешности.
2. Итерационные методы. Суть итерационных методов состоит в построении последовательных приближений к решению задачи. Вначале выбирают одно или несколько начальных приближений, а затем последовательно, используя найденные ранее приближения и однотипную процедуру расчета, строят новые приближения. В результате такого итерационного процесса можно теоретически построить бесконечную последовательность приближений к решению. Если эта последовательность сходится (что бывает не всегда), то говорят, что итерационный метод сходится. Отдельный шаг итерационного процесса называется итерацией.
Практически вычисления не могут продолжаться бесконечно долго. Поэтому необходимо выбрать критерий окончания итерационного процесса.Ва Критерий окончания связан с требуемой точностью вычислений, а именно: вычисления заканчиваются, когда погрешность приближения не превышает заданной величины.
Оценки погрешности приближения, полученные до вычислений, называют априорными оценками (от лат. a'priori тАУ "до опыта"), аВа соответствующие оценки, полученные в ходе вычислений называют апостериорными оценками (от лат. a'posteriori тАУ "после опыта").
Важной характеристикой итерационных методов является скорость сходимости метода. Говорят, что метод имеет -ый порядокВа сходимости если
|xn+1 - x*| = C|xn - x*|p,
где xn и xn+1 тАУ последовательные приближения, полученные в ходе итерационного процесса вычислений, x* тАУ точное решение, C тАУ константа, не зависящая от . Говорят, что метод сходится со скоростью геометрической прогрессии со знаменателем q < 1, если для всех справедлива оценка:
|xn - x*| £Ва Cqn.
Итерационный процесс называется одношаговым, если для вычисления очередного приближения xn+1 используется только одно предыдущее приближение xn и k тАУшаговым, если для вычисления xn+1 используются k предыдущих приближений xn-k+1, xn-k+2, тАж, xn.
Тема 2. Решение нелинейных уравнений
2.1 Постановка задачи
Пусть дана некоторая функция f(x) и требуется найти все или некоторые значения x, для которых
f(x) = 0.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.1)
Значение x*, при котором f(x*) = 0, называется корнем (или решением) уравнения (2.1).
Относительно функции f(x) часто предполагается, что f(x) дважды непрерывно дифференцируема в окрестности корня.
Корень x* уравнения (2.1) называется простым, если первая производная функции f(x) в точке x* не равна нулю, т. е. f '(x*) 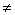 Ва0. Если же f '(x*) = 0, то корень x* называется кратным корнем.
Ва0. Если же f '(x*) = 0, то корень x* называется кратным корнем.
Геометрически корень уравнения (2.1) есть точка пересечения графика функции y = f(x) с осью абсцисс. На рис. 2.1 изображен график функции y = f(x), имеющей четыре корня: два простых (x и x
и x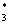 ) и два кратных (x
) и два кратных (x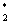 и x
и x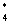 ).
).

Рис. 2.1.
Большинство методов решения уравнения (2.1) ориентировано на отыскание простых корней уравнения (2.1).
2.2 Основные этапы отыскания решения
В процессе приближенного отыскания корней уравнения (2.1) обычно выделяют два этапа: локализация (или отделение) корня и уточнение корня.
Локализация корня заключается в определении отрезка [a, ], содержащего один и только один корень. Не существует универсального алгоритма локализации корня. В некоторых случаях отрезок локализации может быть найден из физических соображений. Иногда удобно бывает локализовать корень с помощью построения графика или таблицы значений функции y = f(x). На наличие корня на отрезке [a, ] указывает различие знаков функции на концах отрезка. Основанием для этого служит следующая теорема математического анализа.
Теорема 2.1. Если функция f непрерывна на отрезке [a, ] и принимает на его концах значения разных знаков, так, что f(a)f() < 0, то отрезок [a, ] содержит по крайней мере один корень уравнения f(x) = 0.
Однако, корень четной кратности таким образом локализовать нельзя, так как в окрестности такого корня функция f(x) имеет постоянный знак.
На этапе уточнения корня вычисляют приближенное значение корня с заданной точностью e > 0. Приближенное значение корня уточняют с помощью различных итерационных методов. Суть этих методов состоит в последовательномВа вычисленииВа значений x0, x1, тАж, xn, тАж, которые являются приближениями к корню x*.
2.3 Метод деления отрезка пополам (метод дихотомии, метод бисекции)
Метод деления отрезка пополам является самым простым и надежным способом решения нелинейного уравнения.
Пусть из предварительного анализа известно, что корень уравнения (2.1) находится на отрезке [a0, 0], т. е. x*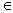 [a0, 0], так, что f(x*) = 0.
[a0, 0], так, что f(x*) = 0.
Пусть функция f(x) непрерывна на отрезке [a0, 0] и принимает на концах отрезка значения разных знаков, т.е.
f(a0)f(0) < 0.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.2)
Разделим отрезок [a0, 0] пополам. Получим точку x0 = 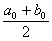 . Вычислим значение функции в этой точке: f(x0). ЕслиВа f(x0) = 0, то x0 тАУ искомый корень, и задача решена. Если f(x0)
. Вычислим значение функции в этой точке: f(x0). ЕслиВа f(x0) = 0, то x0 тАУ искомый корень, и задача решена. Если f(x0)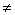 0, то f(x0) тАУ число определенного знака: f(x0) > 0, либо f(x0) < 0. Тогда либо на концах отрезка [a0, x0], либо на концах отрезка [x0, 0] значения функции f(x) имеют разные знаки. Обозначим такой отрезокВа [a1, 1]. Очевидно, что x*
0, то f(x0) тАУ число определенного знака: f(x0) > 0, либо f(x0) < 0. Тогда либо на концах отрезка [a0, x0], либо на концах отрезка [x0, 0] значения функции f(x) имеют разные знаки. Обозначим такой отрезокВа [a1, 1]. Очевидно, что x*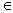 [a1, 1], и длина отрезка [a1, 1] в два раза меньше, чем длина отрезка [a0, 0]. Поступим аналогично с отрезком [a1, 1]. В результате получим либо корень x*, либо новый отрезок [a2, 2], и т.д. (рис. 2.2).
[a1, 1], и длина отрезка [a1, 1] в два раза меньше, чем длина отрезка [a0, 0]. Поступим аналогично с отрезком [a1, 1]. В результате получим либо корень x*, либо новый отрезок [a2, 2], и т.д. (рис. 2.2).
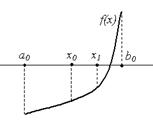
Рис. 2.2
Середина n-го отрезка xn = 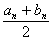 . Очевидно, что длина отрезка [an, n] будет равна
. Очевидно, что длина отрезка [an, n] будет равна 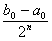 , а т. к. x*
, а т. к. x*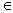 [an, n], то
[an, n], то
| xn тАУ x*| £  £
£ 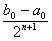 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.3)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.3)
Погрешность метода. Оценка (2.3) характеризует погрешность метода деления отрезка пополам и указывает на скорость сходимости: методВа сходится со скоростью геометрической прогрессии, знаменатель которой q = 1/2. Заметим, что оценка (2.3) является априорной.
Критерий окончания. Из соотношения (2.3) следует, что при заданной точности приближения eвычисления заканчиваются, когда будет выполнено неравенствоВа n тАУВа an < 2eили неравенствоВа > log2((0Ва тАУВа a0)/e) тАУ 1. Таким образом, количество итераций можно определить заранее. За приближенное значение корня берется величина xn.
Пример 2.1.
Найдем приближенно x = 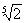 Вас точностью = 0.01. Эта задача эквивалентна решению уравнения x5 тАУ 2 = 0, или нахождению нуля функции f(x) = x5 тАУ 2. В качестве начального отрезка [a0, 0] возьмем отрезок [1, 2]. На концах этого отрезка функция принимает значения с разными знаками: f(1) < 0, f(2) > 0.
Вас точностью = 0.01. Эта задача эквивалентна решению уравнения x5 тАУ 2 = 0, или нахождению нуля функции f(x) = x5 тАУ 2. В качестве начального отрезка [a0, 0] возьмем отрезок [1, 2]. На концах этого отрезка функция принимает значения с разными знаками: f(1) < 0, f(2) > 0.
Найдем число n делений отрезкаВа [1, 2], необходимых для достижения требуемой точности. Имеем:
| xn тАУ x*| £Ва 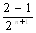 ВаВа=
ВаВа=  Ва£Ва 10-2,
Ва£Ва 10-2,
n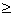 6.
6.
Следовательно, не позднее 6-го деления найдем 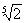 Вас требуемой точностью,
Вас требуемой точностью, 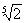 ВаВ» 1.1484. Результаты вычислений представлены в таблице 2.1.
ВаВ» 1.1484. Результаты вычислений представлены в таблице 2.1.
Таблица 2.1
| n | 0ВаВаВаВаВаВаВаВаВаВаВаВа 1ВаВаВаВаВаВаВаВаВаВаВаВа 2ВаВаВаВаВаВаВаВаВаВаВаВа 3ВаВаВаВаВаВаВаВаВаВаВаВа 4ВаВаВаВаВаВаВаВаВаВаВаВа 5ВаВаВаВаВаВаВаВаВаВаВа 6 |
an | 1.0000ВаВа 1.0000Ва Ва1.0000ВаВаВа 1.1250ВаВа 1.1250ВаВаВа 1.1406 1.1406 |
n | 2.0000 Ва1.5000ВаВаВа 1.2500ВаВаВа 1.2500ВаВа 1.1875ВаВа 1.1875Ва 1.1562 |
xn | 1.5000Ва 1.2500Ва Ва1.1250ВаВаВа 1.1875 ВаВаВа1.1406ВаВаВа 1.1562Ва 1.1484 |
Зн f(an) | -ВаВаВаВаВаВаВаВаВаВаВаВаВа -ВаВаВаВаВаВаВаВаВаВаВаВа -ВаВаВаВаВаВаВаВаВаВаВаВаВа -ВаВаВаВаВаВаВаВаВаВаВаВаВа -ВаВаВаВаВаВаВаВаВаВаВаВа -ВаВаВаВаВаВаВаВаВаВаВаВа - |
Зн f(n) | +ВаВаВаВаВаВаВаВаВаВаВаВа +ВаВаВаВаВаВаВаВаВаВаВа +ВаВаВаВаВаВаВаВаВаВаВаВа +ВаВаВаВаВаВаВаВаВаВаВаВа +ВаВаВаВаВаВаВаВаВаВаВаВа +ВаВаВаВаВаВаВаВаВаВаВа + |
f(xn) | 5.5938Ва 0.7585Ва -0.2959ВаВа 0.1812ВаВа -0.0691ВаВаВа 0.0532Ва -0.0078 |
n тАУ an | 1.0000Ва 0.5000Ва Ва0. 2500ВаВа 0.1250ВаВаВа 0.0625ВаВаВа 0.0312 ВаВа0.0156 |
2.4 Метод простых итераций
Пусть уравнение (2.1) можно заменить эквивалентным ему уравнением
x = j(x).ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.4)
Например, уравнение  ВаВатАУВа 0.5 = 0 можно заменить эквивалентным ему уравнением x = 0.5sinx.
ВаВатАУВа 0.5 = 0 можно заменить эквивалентным ему уравнением x = 0.5sinx.
Выберем каким-либо образом начальное приближение x0. Вычислим значение функции j(x) при x = x0 и найдем уточненное значение x1 = j(x0). Подставим теперь x1 в уравнение (2.4) и получим новое приближение x2 = j(x1) и т. д. Продолжая этот процесс неограниченно, получим последовательность приближений к корню:
xn+1 = j(xn).ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.5)
Формула (2.5) является расчетной формулой метода простых итераций.
Если последовательность {xn} сходится при nВо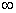 , т. е. существует
, т. е. существует
x* = 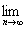 Ваxn ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(2.6)
Ваxn ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(2.6)
и функция j(x) непрерывна, то, переходя к пределу в (2.5) и учитывая (2.6), получим:
x* = 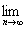 xnВа =
xnВа = 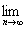 j(xn -1) = j(
j(xn -1) = j(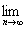 xn -1) = j(x*).
xn -1) = j(x*).
Таким образом, x* = j(x*), следовательно, x* тАУВа кореньВаВаВа уравнения (2.4).
Сходимость метода. Сходимость метода простых итераций устанавливает следующая теорема.
Теорема 2.2. Если в интервале, содержащем корень x*Вауравнения (2.4), а также его последовательные приближения x0, x1, тАж, xn, тАж, вычисляемые по формуле (2.5), выполнено условие:
|j'(x)| £ q < 1,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.7)
то x* =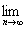 Ваxn.
Ваxn.
т. е. итерационный процесс сходится и справедлива следующая оценка погрешности:
|xn тАУ x*| £Ва qn|x0 тАУ x*|ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.8)
Оценка (2.8) является априорной. Она показывает, что метод простой итерации сходится со скоростью геометрической прогрессии с знаменателем q. Чем меньше q, тем выше скорость сходимости.
Как следует из теоремы 2.2, условие (2.7) является достаточным для сходимости метода простых итераций. Его выполнение гарантирует сходимость процесса (2.5), но невыполнение условия (2.7), вообще говоря, не означает, что итерационный процесс будет расходиться.
На рис. 2.3 тАУ 2.6 показаны четыре случая взаимного расположения линий y = x и y = j(x) и соответствующие итерационные процессы.
Рис. 2.3 и 2.4 соответствуют случаю |j'(x)| < 1, и итерационный процесс сходится. При этом, если j'(x) > 0 (рис. 2.3), сходимость носит односторонний характер, а если j'(x)< 0 (рис. 2.4), сходимость носит двусторонний, колебательный характер. Рис. 2.5 и 2.6 соответствуют случаю |j'(x)|Ва > 1 тАУ итерационный процесс расходится. При этом может быть односторонняя (рис. 2.5) и двусторонняя (рис 2.6) расходимость.
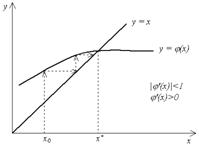
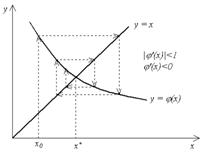

Рис. 2.3ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Рис. 2.4ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВа Рис. 2.5
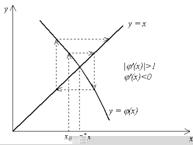
Рис. 2.6
Погрешность метода. Если известна величина q в условии (2.7), то применима следующая апостериорная оценка погрешности:
|xn тАУ x*| £Ва 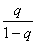 |xn тАУ xn тАУ 1|, n > 1.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.9)
|xn тАУ xn тАУ 1|, n > 1.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.9)
Критерий окончания. Из оценки (2.9) вытекает следующий критерий окончания итерационного процесса. Вычисления следует продолжать до выполнения неравенства
|xn тАУ xn тАУ 1| < 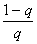 e.
e.
Если это условие выполнено, то можно считать, что xn является приближением кВа x* с точностью e.
Если q £ 0.5, то можно пользоваться более простым критерием окончания:
|xn тАУ xn тАУ 1| < e.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.10)
Пример 2.2.
Используем метод простой итерации для решения уравнения f(x) = sin x тАУ x2 = 0с точностью e = 0.001.
Преобразуем уравнение к виду (2.4):
x = 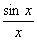 , т. е. j(x)=
, т. е. j(x)= 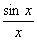 .
.
Нетрудно убедиться, что корень уравнения находится на отрезке [/6, /3]. Например, вычислив значения f(x)на концах отрезка, получим: f(/6)> 0, а f(/3)< 0, т. е. функция на концах отрезка имеет разные знаки, что в соответствии с теоремой 2.1 указывает на то, что внутри отрезка есть корень. Расположение корня наглядно иллюстрирует рис.2.7.
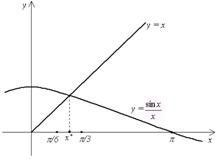
Рис. 2.7
Подсчитаем, первую и вторую производные функции j(x):
j'(x) = 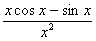 , j"(x) =
, j"(x) =  .
.
Так как j"(x) > 0 на отрезке [/6, /3], то производная j'(x) монотонно возрастает на этом отрезке и принимает максимальное значение на правом конце отрезка, т. е. в точке /3. Поэтому, справедлива оценка:
|j'(x)| £ |j'(/3)| В» 0.312.
Таким образом, условие (2.7) выполнено, q < 0.5, и можно воспользоваться критерием окончания вычислений в виде (2.10). В табл. 2.2 приведены приближения, полученные по расчетной формуле (2.5). В качестве начального приближения выбрано значение x0 = 1.
Таблица 2.2
| xn |
0 1 2 3 4 5 | 1 0.8415 0.8861 0.8742 0.8774 0.8765 |
Критерий окончания выполняется при = 5, |x5 тАУ x4| < 0.001. СходимостьВа двусторонняя, качественный характер такой сходимости представлен на рис. 2.4. Приближенное значение корняВа с требуемой точностью x* 0.8765.
0.8765.
2.5 Метод Ньютона (метод касательных)
Метод Ньютона является наиболее эффективным методом решения нелинейных уравнений.
Пусть корень x* Î [a, ], так, что f(a)f() < 0. Предполагаем, что функция f(x) непрерывна на отрезке [a, ] и дважды непрерывно дифференцируема на интервале (a, ).Ва Положим x0 = b. Проведем касательную к графику функции y = f(x) в точке B0 = (x0, f(x0)) (рис. 2.8).
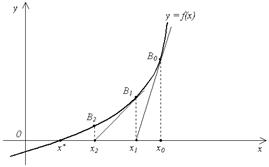
Рис. 2.8
Уравнение касательной будет иметь вид:
y тАУ f(x0) = f '(x0)(x тАУ x0).ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.11)
Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью OX, т. е. положив в (2.11) y = 0, x = x1:
x1 = x0Ва тАУ 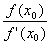 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.12)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.12)
Аналогично поступим с точкой B1(x1, f(x1)), затем с точкой B2(x2, f(x2)), и т. д. в результате получим последовательность приближений x1, x2, тАж, xn , тАж,причем
xn +1 = xnВа тАУ 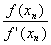 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.13)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.13)
Формула (2.13) является расчетной формулой метода Ньютона.
Метод Ньютона можно рассматривать как частный случай метода простых итераций, для которого
j(x) = x -  .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(2.14)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(2.14)
Сходимость метода. Сходимость метода Ньютона устанавливает следующая теорема.
Теорема 2.3. ВаПусть x* ВатАУ простой корень уравнения Ваf(x) = 0, и в некоторой окрестности этого корня функция f дважды непрерывно дифференцируема. Тогда найдется такая малая -окрестность корня x*, что при произвольном выборе начального приближения x0из этой окрестности итерационная последовательность, определенная по формуле (2.13) не выходит за пределы этой окрестности и справедлива оценка:
|xn + 1 тАУ x*| £ C |xn тАУ x*|2, n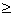 Ва0,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.15)
Ва0,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.15)
где С = -1. Оценка (2.15) означает, что метод сходится с квадратичной скоростью.
Сходимость метода Ньютона зависит от того, насколько близко к корню выбрано начальное приближение. Неудачный выбор начального приближения может дать расходящуюся последовательность. Полезно иметь в виду следующее достаточное условие сходимости метода. Пусть [a, b] тАУ отрезок, содержащий корень. Если в качестве начального приближения x0выбрать тот из концов отрезка, для которого
f(x)f"(x)³0,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.16)
то итерации (2.13) сходятся, причем монотонно. Рис. 2.8 соответствует случаю, когда в качестве начального приближения был выбран правый конец отрезка: x0 = b.
Погрешность метода. Оценка (2.15) является априорной и неудобна для практического использования. На практике удобно пользоваться следующей апостериорной оценкой погрешности:
|xn тАУ x*| £Ва |xn тАУ xn тАУ 1|. ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(2.17)
Критерий окончания. Оценка (2.17) позволяет сформулировать следующий критерий окончания итераций метода Ньютона. При заданной точности e > 0 вычисления нужно вести до тех пор, пока не будет выполнено неравенство
|xn тАУ xn тАУ 1| < e.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.18)
Пример 2.3.
Применим метод Ньютона для вычисления  . где a > 0, тАУ натуральное число. Вычисление
. где a > 0, тАУ натуральное число. Вычисление  Ваэквивалентно решению уравнения xp = a. Таким образом, нужно найти корень уравнения f(x) = 0, f(x) = xpтАУ a, f '(x) = pxp тАУ 1. Итерационная формула метода (2.13) примет вид:
Ваэквивалентно решению уравнения xp = a. Таким образом, нужно найти корень уравнения f(x) = 0, f(x) = xpтАУ a, f '(x) = pxp тАУ 1. Итерационная формула метода (2.13) примет вид:
xn +1 = xnВа тАУ  Ва=
Ва=  xn Ва+
xn Ва+ 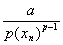 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.19)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.19)
Используя формулу (2.19), найдемВа 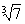 с точностью e= 10-3.
с точностью e= 10-3.
xn +1 = 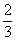 xn Ва+
xn Ва+ 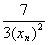 .
.
Простой корень уравнения x3 тАУ 7 = 0 расположен на отрезке [1, 2]. Действительно, на концах отрезка [1, 2] функция f(x) = x3 тАУ 7 принимает разные знаки, f (1) < 0,Ва f (2) > 0. Кроме того, при x = 2 выполнено достаточное условие сходимости (2.16): f (2)f" (2)³0.
Поэтому в качестве начального приближения можно взять x0 = 2.
Результаты приведены в табл. 2.3.
Таблица 2.3
| xn |
0 1 2 3 4 5 | 2 0.8415 0.8861 0.8742 0.8774 0.8765 |
2.6 Метод секущих (метод хорд)
В этом и следующем разделе рассмотрим модификации метода Ньютона.
Как видно из формулы (2.13), метод Ньютона требует для своей реализации вычисления производной, что ограничивает его применение. Метод секущих лишен этого недостатка. Если производную заменить ее приближением:
f'(xn) В» 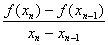 ,
,
то вместо формулы (2.13) получим
xn +1 = xn тАУ. 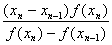 .ВаВаВаВа (2.20)
.ВаВаВаВа (2.20)
Это означает, что касательные заменены секущими. Метод секущих является двухшаговым методом, для вычисления приближения xn +1 Ванеобходимо вычислить два предыдущих приближенияВа xn и xn тАУ 1 , и, в частности, на первой итерации надо знать два начальных значения x0 и x1.
Формула (2.20) является расчетной формулой метода секущих. На рис. 2.9 приведена геометрическая иллюстрация метода секущих.
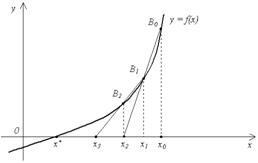
Рис. 2.9
Очередное приближение xn +1 получается как точка пересечения с осью OX секущей, соединяющей точки графика функции f(x)Вас координатами (xn -1, f(xn - 1)) и (xn , f(xn)).
Сходимость метода. Сходимость метода секущих устанавливает следующая теорема.
Теорема 2.4 Пусть x* ВатАУ простой корень уравнения Ваf(x) = 0, и в некоторой окрестности этого корня функция f дважды непрерывно дифференцируема, причем f"(x) ¹ 0. Тогда найдется такая малая -окрестность корня x*, что при произвольном выборе начальных приближений x0 иx1из этой окрестности итерационная последовательность, определенная по формуле (2.20) сходится и справедлива оценка:
|xn + 1 тАУ x*| £ C |xn тАУ x*| p,ВаВаВа ³Ва0,Ва = 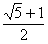 ВаВ» 1.618.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.21)
ВаВ» 1.618.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.21)
Сравнение оценок (2.15) и (2.21) показывает, что < 2, и метод секущих сходится медленнее, чем метод Ньютона. Но в методе Ньютона на каждой итерации надо вычислять и функцию, и производную, а в методе секущих тАУ только функцию. Поэтому при одинаковом объеме вычислений в методе секущих можно сделать примерно вдвое больше итераций и получить более высокую точность.
Так же, как и метод Ньютона, при неудачном выборе начальных приближений (вдали от корня) метод секущих может расходиться.Ва Кроме того применение метода секущих осложняется из-за того, что в знаменатель расчетной формулы метода (2.20) входит разность значений функции. Вблизи корня эта разность мала, и метод теряет устойчивость.
Критерий окончания. Критерий окончания итераций метода секущих такой же, как и для метода Ньютона. При заданной точности e > 0 вычисления нужно вести до тех пор, пока не будет выполнено неравенство
|xn тАУ xn тАУ 1| < e.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.22)
Пример 2.4.
Применим метод секущих для вычисления положительного корня уравнения 4(1 тАУ x2) тАУ ex = 0 с точностью e= 10-3.
Корень этого уравнения находится на отрезке [0, 1], так как f (0) = 3 > 0, а f (1) =Ва тАУe Ва< 0. Подсчитаем вторую производную функции: f "(x) = тАУ8 тАУ ex. Условие f(x)f " (x)³0 выполняется для точки = 1. В качестве начального приближения возьмем x0 = = 1. В качестве второго начального значения возьмем x1= 0.5. Проведем вычисления по расчетной формуле (2.20). Результаты приведены в табл. 2.4.
Таблица 2.4