Основы статистики

1. Исторические аспекты развития статистики

Термин Влст-каВ» произошел от лат. слов stato (гос-во) status (положение вещей, полит. сост-ие). Ст-ка им-т многовек-ую ист-ию. Её возн-е и разв-е обусл-ны общ-ми потр-тями: подсчет насел-я, скота, учета зем-ых угодий, имущ-ва и т.д. Наиб. ранние сведения о таких работах в Китае относятся к 13 в. до нашей эры. В Древнем Риме провод-сь учеты своб. граждан и их имущ-ва. Счит-ся, что основы стат. науки заложены англ. экон-том У.Петти Он рассм-л ст-ку как науку об упр-ии. В 1746г. нем. проф-р фил-фии и права Ахенваль впервые в Марбургском унив-те начал читать новую дисц-ну, назв-ную им ст-кой. В разв-ии ст-ки видное место принадл-т представ-ям отеч. науки и практики. В эпоху Петра I ст-ка трактов-сь преим-но как описат-ная наука. Но уже со 2й пол. XIX в. выдвиг-ся познават-е знач-е ст-ки. Проф. петербургского унив-та Янсон назвал ст-ку общ-ой наукой. Видный экон-ст Чупров отмечал необх-сть массового стат. иссл-ия при помощи метода колич-го набл-ия большого числа факторов для того, чтобы описать общ-ые явл-я, подметить законы и опред-ть причины, их вызвавшие. Развитие ст-ки в России тесным образом связано с созданной после отмены крепост. права земской ст-кой, кот. польз-сь заслуж-ым авторитетом за объект-сть и професс-зм. Ист-ия развития ст-ки показ-ет, что стат. наука сложилась в рез-те теорет. обобщения накопл-го человеч-вом передового опыта учетно-стат. работ, обусл-ых, прежде всего, потреб-тями упр-ния жизни общ-ва.

2. Общ. хар-ка предм. ст-ки

Ст-ка тАУ это наука, изуч-ая зак-ти массовых однородных соц.-экон. явл-ий на основе стат. данных (с учетом действия случ. факторов). Предмет ст-ки тАУ колич-ая сторона, включ-ая принципы, методы, положения, характ-щая изуч-мые СЭЯП. Ст-ка тАУ это иск-во измерения полит.,соц.,экон. проц-сов.Стр-ра теории ст-ки: 1)общ. орг.-правовые полож-я, задачи ст-ки, орг-ция гос.стат. служб. 2) описат-ая ст-ка (сбор стат. данных-стат. набл-е, сводка и групп-ка данных, графич. и табл.стат. инф-ции).3) аналит-ая ст-ка (стат. показ-ли, выборочное набл-ие, изуч-ие взаимосвязей СЕЯП, изуч-е динамики СЭЯП,врем-ые ряды, индексные методы). Задачи ст-ки: 1)всесторннне иссл-ие соц.-экон.явл-ий на федер.,регион. и муниц.-ом Ур-нях.2)разраб-ка научн. методов по сбору, учету и обраб-ке стат. данных.3)прогноз-ие развития СЭЯП на всех ур-нях по стат. данным.4)внедрение инф-ных техн-гий с целью повыш-ия оператив-ти сбора, обработки и анализа стат. данных и обеспеч-е треб-ой достоверности.

3. Статистическая методология

Под стат. метод-гией поним. с-иу взаимосвяз-х методов, способов и приемов, напр-х на изучение колич-х зак-тей, массовых общ-ых явл-ий. В основе применения стат. метод-гии лежит понятие стат. иссл-ний тАУ сов-сть 3-х послед-ых стадий, сод-нием кот. соотв-но явл-ся сбор,обработка и анализ клич-ых данных, характер-щих различные стороны СЭЯП. Основой для разработки и применения стат. метод-гии (сов-сти методов и приемов) явл-ся диалектический метод познания, когда общ-ые явления и процессы рассм-ся в развитии, взаимной связи и причинной обусл-сти. Многообразие стат. методов обусл-но сложностью объекта и сложностью и многоэтапностью трех стадий исс-ия экон. явл-й: 1 стад. тАУ сбор первичной инф-ции тАУ метод массового стат. набл-ия, обеспеч-щий репрезентативность инф-ции;

2 стад. тАУ сводка, групп-ка, обработка первичной инф-ции тАУ метод стат. групп-вок матем. ст-ки и ТВ;

3 стад. тАУ обобщение и интерпретация стат. инф-ции тАУ метод обобщения и анализа на основе показ-лей абсолютных отн-ных и средних величин, вариаций динамики, индексов.

На всех стадиях применяются графические, табличные и математические методы.

4. Орг-ция гос-ой и междунар. ст-ки

В масштабе РФ общее рук-во развитием орг-ции, сбора стат. данных и предст-ние её органам гос. упр-ния осущ-ет федер. службы госуд. ст-ки Росстат. Органы Госкомстата сост-ют единую сеть гос. политики. Данные собир-ся по единым стандартам, а их предст-ние явл-ся обяз-ным для хозяйствующих субъектов. В масштабе ЕС координацию осущ-ет Евростат. В мире в рамках ООН создана стат. комиссия ООН, включ-ая стат. бюро и секретариат, кот. включ-ет регион-ые. стат. комиссии и международн. стат институт. 5. Осн. понятия ст-ки

Ст-ка как наука базир-ся на общем и спец-ом понятийно-терминолог. аппарате, в состав кот. входят:1)стат. метод-гия тАУ с-ма методов, способов и приемов, напр-ых на изуч-ие колич-ых зак-тей массовых случ. явл-ий 2) стат. сов-сть тАУ аналог в мат. ст-ке. генер. сов-сть тАУ множ-во Эл-тов, облад-их как общими признаками и характ-ми чертами, так и индивид. особ-тями и различиями. 3)единица сов-сти тАУ это отд-но взятый Эл-т множ-ва, облад-ет опред-ми признаками 4)признак тАУ это св-ва, характ-е черты или особ-ти изуч-ых объектов (явл-ий), выраж-ые колич-но или качеств-но. Признаки: атрибутивные.(качеств-ые), колич-ые (дискретные и непрерывные)5) вариация тАУ изменения признака от одного эл-та сов-сти к другому.6)стат. закон-сть тАУ это вид зак-сти, проявл-ся в большой массе однородных случ. явл-ий, основ. на взаимопогашении в отд-ых и инд-ых различий, закл-ся в том, что средн. рез-тат массы СЯ перестает быть случ-ным.

6. Стат. набл-ние

Стат. набл-ие тАУ это первая стадия стат. иссл-ия, заключ-ся в научно-организац. учете,сборе и рагистрации стат. инф-ции изучаемых явл-ий и процессов. Цель СН тАУ получение достоверной инф-ции для выявления зак-тей развития случ. процесса и явления. Св-ва: 1) выраж-ие опред-ых соцю-экон. типов, им-х научн. и практич. ценность.2) обеспечение полноты, акт-ти, и адекватной инф-ции об изуч-х объектах.

Схема СН: 1) подготовка СН 2) проведение массовго сбора данных 3) всесторонняя проверка рез-тов СН 4) автоматизир-ная обработка 5) предложения по соверш-нию СН. СН имеет след. осн. этапы: 1) планирование 2) разработка рабочей программы 3) непосредственный сбор данных учет и регистрация рез-тов. Треб-ия, предъяв-ые к стат. инф-ции: 1)Достоверность. Обеспечивается научным подходом, компетентностью работников 2) Полнота данных. Обеспечивается научно-обоснованным охватом единиц наблюдения: а) изучением существенных признаков; б) данными за достаточно длительный период времени.3) Своевременность данных. 4) Сопоставимость данных. Обеспечивается едиными стоимостными оценками; едиными территориальными границами.

7. Прог.-метод. вопросы

Одной из важнейших задач, кот. необтАУмо решить при подготовке СН, явл-ся опред-е цели, объекта и единицы наблюдения. Целью практич-ки люб. СН явл-ся получение достоверной инфтАУции о явл-иях и процессах общ-ой жизни, с тем чтобы выявить взаимосвязи факторов, оценить масштабы явления и закономерности его развития. Исходя из задач наблюдения определяются его протАУграмма и формы орг-ии. Объектом наблюдения тАУ совок-сть общ-ых явл-ий или процессов, подлежащих иссл-ию. При устан-ии объекта набл-ия важно строго и точно опред-ть границы изучтАУмой совок-ти. Ед-ца совок-ти тАУ это так наз-ый составной эл-т объекта набл-ния, от кот.поступают сведения о ед-це набл-ния, т. е. кот. служит основой счета и обладает признаками, подлежащими регистрации в процессе наблюдения. Каждое явл-е или процесс общ-ой жизни обладает множ-вом признаков, их характ-щих. Программа СН предст-ет собой сов-сть вопросов, ответы на кот. в процессе набл-ния и должны составить стат. сведения. При разраб-ке программы набл-ния необх-мо учитывать ряд предъявляемых к ней треб-ний. Стат. формуляр тАУ это спец. документ единого образца, в кот. фиксируются ответы на вопросы программы. В завис-ти от конкр-го сод-ния проводимого набл-ния формуляр может наз-ся формой стат. отчетности, переписным или опросным листом, картАУтой, карточкой, анкетой или бланком. Различают два вида формуляров: карточные и списочные. Формуляр-карточка предназнач. для отражения сведений об одной ед-це стат. совок-ти, а списочный формуляр сод-жит сведения о неск-их ед-цах сов-сти. Критический момент СН -т момент времени, к кот.у приурочены регистрируемые в проц-се набл-ния сведения. Сроком набл-ния опред-ся период, в течение кот. должна осущ-ся регис-ция сведений об изучаемом явл-ии.

8. Осн. орган. формы стат. набл-ия

Форма стат. набл-ия: 1) отчетность, получ-ая от предп-ий, орг-ций, учр-ний 2) спец. стат. обследование (переписи, рег-ции, опросы, анкетир-ние) 3) регистры тАУ промышл. предп-тия, стройки. Виды СН: 1) по полноте обхвата ед-ц сов-сти: сплошное, несплошное (выборочное, основного массива, анкетное, монографическое) 2) по учету факторов по времени: текущие (постоянные), периодические, единовременные (перепись). Предост-ние предпр-ми, орг-циями стат. отчетов о своей хоз-ой деят-ти в строго устан-ном порядке называют отчетным способом. Вид СН, предполагающий предост-ние сведений в органы, кот. и ведут набл-ние, в явочном порядке - явочным способом. Если сведения в органы предост-ют корреспонденты, то этот способ - корреспондентский. Предост-ние док-тов, кот. заполняют сами опрашиваемые, а спец-ые работники только обеспеч-ют формулярами, называют способом саморегистрации.

9. Ошибки СН

Ошибки СН тАУ это ошибки репрезентативности и ошибки регистрации. Ошибки репрез-сти показ-ют, в какой степени выборочная сов-сть представляет генер-ую сов-сть. Эти ошибки возн. потому, что набл-нию подвергается только часть ед-ц изуч-мой сов-сти, и сведения эти не могут абсолютно точно отобразить св-ва всей массы явл-ий сов-сти. Возник-щие в рез-те неправ-го устан-ия фактов ошибки регистрации можно подразделить на: 1) случ-ые тАУ это ошибки, кот. могут дать искажения как в одну, так и в другую сторону; 2) систематич-е ошибки, возник-щие вследствие нарушения принципов непреднамеренного отбора единиц изуч-мой сов-сти. Систематич-е ошибки опасны, потому что они влияют на полученные итоговые показ-ли; 3) преднамеренные ошибки возникают вследствие умышленного искажения фактов.

10. Сводка

Сводка тАУ это комплекс послед-ых операция по обобщению инф-ции, получ-ой в руз-те СН с целью выявления осн. св-в, черт и закон-тей изуч-го явл-ия в целом. Сводка как правило, произв-ся на основе предварит-ого анализа изуч-го проц-са. Типология сводок: 1) по глубине обработки матер-ла: простая (операция общих итогов), сложн. (подсчет итогов по каждой группе и предст-ние рез-тов в виде стат. таблиц 2) по форме обработки материала: централиз-ая (данные сосредот-ся в одном месте, сводятся по разработ-ой методике), децентрализ-ая (обобщение матр-ла осущ-ся по иерархической лестнице, подвергаясь соответ-щей обраб-ке). 3) по степени автоматизации: ручная, автоматизир-ая.

11. Группировка

Групп-ка тАУ это проц-с обр-ния однородн. групп на основе расчленения стат. совок-сти на части или объед-ния изуч-ых ед-ц в частные совок-сти по существ-ым признакам.

Виды 1) типологич-ая гр-ка - разделение качественно разнородной совок-сти на классы или однородные группы; 2) структ-ая гр-ка, в кот. происх-т разделение однородной совок-сти на группы, характ-щие ее стр-ру по какому-либо варьируемому признаку; 3) аналитич-я гр-ка, выявляющая взаимосвязи между изуч-ми явл-ми и их признаками (факторными и результ-ми); 4) комбинированная гр-ка, образ-ная по двум или более признакам. Если совок-сть сост. из большого числа ед-ц и распред-ие ед-ц по группировочному признаку близко к норм-му, для опред-ия кол-ва групп (m) исп-ют формулу Стерджесса:

m = 1+3,322В·lg N, где N тАУ численность единиц совокупности. Если вариация признака происх-ит в сравнит-но узких границах и распред-ие носит равномерн. хар-тер, то строят групп-ку с равными интервалами:

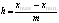
где h тАУ величина интервала; x_max, x_min тАУ максимальное и минимальное значения группировочного признака в совокупности; m тАУ число групп.

12. Многомерные группировки

МГ исп-ся в ст-ке, когда проводится групп-ка по неск-им признакам. Прим-ют на практике метод многомерной класс-ции с исп-нием вычисл-х машин. Наиб. простым методом многомерной класс-ции явл-ся многомерная средняя, кот. наз-ся средняя величина неск-их признаков для одной единицы совок-сти. Она опред-ся из отн-ных величин, как правило, из отн-ний абсолютных знач-й признаков для единицы к средним значениям этих признаков.

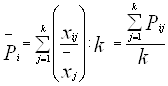где

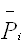- многомерное среднее для i-той единицы

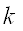-число признаков;

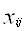-абсолютное значение признака x для i-той единицы;

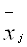-среднее значение признака x

13. Ряды распр-ний. Дискр. вар. ряд

Важн-шей частью стат. анализа явл-ся построение рядов распред-ия (струк-рной групп-ки) с целью выделения характ-ых св-в и закон-тей изуч-ой сов-сти. В завис-ти от того, какой признак (колич-ый или качест-ый) взят за основу групп-ки данных, различ. соотв-но типы рядов распр-ния. Если за основу групп-ки взят качеств-ый признак, то такой ряд распр-ния наз.
атрибутивным (распр-ние по видам труда, по полу, по проф-сии, по религ. признаку и т.д.). Если ряд распр-ния построен по колич-му признаку, то такой ряд наз.
вариационным. Построить вариац-ый ряд - значит упорядочить колич-ное распр-ние ед-ц совок-сти по знач-ям признака, а затем подсчитать числа ед-ц совок-сти с этими знач-ми (построить групповую таблицу). Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд. Дискр. ряд - это такой вариац. ряд, в основу построения кот. положены признаки с прерывным изм-нием (дискретные признаки). К последним можно отнести кол-во детей в семье, число раб-ков на предп-ии и т.д. Эти признаки могут принимать только конечное число опред-х знач-ий. Дискр. вар. ряд предст. таблицу, кот. сост. из 2х граф. В 1-й графе указ-ся конкретное знач-е признака, а во 2й - число ед-ц совок-сти с опред-ым знач-ем признака. Частота (частота повторения) - число повторений отд-го варианта знач-ий признака, обознач._i , а сумма частот, равная объему иссл-мой совок-ти, обознач. 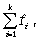где k - число вариантов знач-й признака При построении вариац. ряда с интервальными знач-ми прежде всего необх-мо устан-ть величину интервала i, кот. опред-ся как отн-ние размаха вариации R к числу групп m:

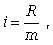
где R = x_max - x_min ; m = 1 + 3,322 lgn (формула
Стерджесса); n - общее число единиц совокупности.

14. ИВР и порядок его построения

ИВР - это ряд, который отражает непрерывную вариацию признака. алгоритм построения: 1) Исходя из объема выборки n, определить количество интервалов k. 2. Вычислить размах ряда: R=Xmax-Xmin 3. Определить ширину интервала: h=R/(k-1) 4. Найти начало первого интервала X0 = Xmin - h/2 5. Составить интервальный вариационный ряд. ГРАФИЧЕСКИМ изображением интервального вариационного ряда является гистограмма.

15. Стат таблица

Стат. таблица тАУ это форма сист-го рац-го и наглядного излож. стат. цифрового материала, хар-его изучаемые явления или процессы. Виды стат-х таблиц. Табл. различаются по построению подлежащего, разработке сказуемого и по целям исследования. В завис. от построения подлежащего статистические таблицы подразделяются на три вида 1)простые(такие стат. таблицы, в подлежащих которых имеется только перечень показателей, раскрывающих содержание подлежащего и нет группировок их. Иногда такие таблицы называются перечневыми) 2) групповые (такие стат. таблицы, в кот изучаемый объект разделен в подлежащем на группы по тому или иному признаку) 3) комбинированные(такая таблица, в которой в подлежащем дана группировка единиц совокупности по двум и более признакам, взятым в комбинации( изучаемый объект разбит на группы), а внутри групп на подгруппы) Сказуемое табл. так же может быть разработано по-разному. Если сказуемое представлено простым перечнем ряда показателей, то его разработка является простой, а если множеством показателей, в комбинации дополняющих друг друга, то сложной. Правила построения стат. таблиц: 1) компактность 2) четкость и лаконичность заголовков 3) наличие итоговой строки

16. Статистический график

Стат. график - это чертеж, на котором стат. сов-сти, хар-емые опред. показателями, описываются с пом. условных геом-их образов или знаков. классификация по форме граф. образа: 1) линейные (статистические кривые) 2) плоскостные (полосовые, круговые, секторные, фигурные, фоновые, точечные, столбиковые, квадратные 3) объемные (поверхностные распределения) По способу построения стат. графики делятся на 1) диаграммы 2) стат. карты. Диаграммы - наиболее распространенный способ графических изображений, чертеж, на котором стат. данные представлены при помощи геом-х фигур или знаков, а территория, к которой относятся эти данные, указана только словесно. Если диаграмма наложена на географическую карту или на план территории, к которой относятся статданные, то график называется картодиаграммой. Если же статистические данные изображены путем штриховки или раскраски соотв. территории на геогр. карте или плане, то график называется картограммой.

17. Стат. показатели

Стат. показатели - это количественная характеристика социально - экономических явлений и процессов в условиях качественной определенности. Конкретный статистический показатель характеризует размер, величину изучаемого явления или процесса в данном месте и в данное время (под привязкой к месту понимается отношение показателя к какой-либо территории или объекту). Классификация: 1) по хар-ке изучаемого СЭЯП а) конкретные (прибыль предприятия за 1 квартал 2010) б) показатель-категория(валовая прибыль пром. предприятия) 1) индивидуальные (размер вклада в банк) 2) сводные: а)объёмные б)расчетные по форме выражения: 1) абсолютные 2) относительные 3) средние по временному фактору: 1) моментные 2) интервальные по кол-ву хар-к объектов: 1) однообъектные 2) межобъектные по пространственной определенности: глобальные, общетерриториальные, федеральные, региональные

18. Абсолютные и относительные статистические показатели

АСП-это пок-ли, хар-е абсолютные размеры изуч. явл-я и процесса, а также предст-ый общий объем иссл-ой совок-сти.АСП (индивид-ые, суммарные) осн. единицы измерения: 1) натуральные(кг,м,км) 2) у словно-натуральные, 3) стоимостные (р,тВм), 4) трудовые. АСП играет важную роль в иссл-ии СЭЯП. недостаток-невозможно проследить! ОСП- пок-ль,кот. форм-ся в виде отношения двух АСП. В числ-ле АСП - текущий или сравнительный. В знам-ле - АСП наз-ся базой сравненийсуществуют (ОВПЗ, ОСПВП, ОСПД, ОСПС, ОСПК, ОСПСр, ОСПИ, ОСПД)

19. Средняя величина

Средняя величина - обобщенная колич. хар-ика стат сов-сти в конкр-х усл-ях места и времени. Сущность средней состоит в том, что она отражает типичный уровень признака и абстрагируется от инд-х особенностей, присущих отдельным единицам. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу. В каждом конкретном случае для реализации исходного соотношения требуется одна из форм средней величины. Все виды средних объединяются в общей формуле средней степенной (при различной величине к): 1)простая 2)взвешенная где к- пок-ль степени, опр-щий вид сред. величины; х -сред вел исс-мого явления; xi - i-ый вариант осредняемого признака (i = 1, n) fi - вес i-гo варианта. В зав от к различают след виды ср. величин: к = -1 - средняя гармоническая; к = 0 - средняя геометрическая; к=1 - средняя арифметическая; к = 2 - средняя квадратическая.

20. Средняя арифметическая и ее свойства

СА - Наиболее распространенный вид средних величин, может быть простой или взвешенной.САпростая применяется, когда значение вариантов встречается по одному числу раз. СА взвешенная применяется, когда отдельное значение признака повторяется неодинаковое кол-во раз, т.е. она исп-ся в расчетах средней по сгрупп-м данным или ДВР и ИВР. свойства 1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты. 2. Если от каждой варианты отнять (прибавить) какое-либо произвольное число, то новая средняя уменьшится (увеличится) на то же число: 3. Если каждую варианту умножить (разделить) на какое-то произвольное число, то СА увеличится (уменьшится) во столько раз 4. Если все частоты (веса) разделить или умножить на какое-либо число, тоСА от этого не изменится. 5.Сумма отклонений отдельных вариантов от СА всегда равняется нулю.

21 Виды средних величин и особенности их использования при статистической обработке данных

Средняя гарм - это величина, обратная средней арифметической, когда к = -1. Когда стат. инф-я не содержит частот по отд-м вариантам совокупности, а представлена как их произв-ие, прим-ся ф-ла ср гарм взвешенной. Когда объемы явлений, т.е. произведения (w, = w,). по каждому признаку равны, применяется ср гарм. простая. Ср геом - это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии, когда к = О, Ср геом. исп-тся в расчетах среднегодовых темпов роста и для опр-я равноудаленной величины от мин-го и макс-го значений признака.(простая и взвешенная)

22. Структ. хар-ки вар.ряда

В ДР мода- это варианта с наибольшей частотой. В ИР модой считают центральный вариант модального интервала, т.е. того интервала, который имеет наибольшую частоту (частотность). Мода для ИР: где хм - нижняя граница модального интервала, д/ - величина модального интервала, /w - частота, соответствующая модальному интервалу. 4 /v/ - частота, предшествующая модальному интервалу, /д/ - частота интервала, следующего за модальным. Медиана (Me) - это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значение варьирующего признака меньше, чем средний вариант, а другая - больше. Для ранжированного ряда (т.е. построенного в порядке возрастания или убывания индивидуальных величин) с нечетным числом, членов медианой является варианта, расположенная в центре ряда. Для ранжированного ряда с четным числом членов медианой будет средняя арифметическая из двух смежных вариант. Для ИВР: Медианный интервал - это интервал, где сумма накопленных частот составляет половину (или больше) всей суммы частот ряда.

23. Вариация признака

Для хар-ки размера вариации в статистике прим-ся абсолютные показатели вариации: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение и дисперсия. Размах вариации (размах колебаний)- разность между максимальным и минимальным значениями признака в совокупности. Размах вариации зависит от величины только крайних значений признака. Более точно характеризуют вариацию признака показатели, основанные на учете колеблемости всех значений признака, - среднее линейное отклонение и среднее квадратическое отклонение. Квадрат среднего квадратического отклонения называется дисперсией Для оценки интенсивности вариации, а также для сравнения ее величины в разных сов-х или по разным признакам используют относ пок-ли вариации, которые рассч-ся как отношение абсолютных пок-елей вариации к средней величине признака: относительный размах вариации (коэффициент осцилляции), относительное линейное отклонение и др. Наиболее часто на практике приним коэффициент вариации, кот. Предст. собой относ квадратическое отклонение

24. Вар. альтер признаки

Вар. Альтер. признаки - те которыми обладают одни единицы совок и не обладают другие. Пример: Бракованная продукция; работа по получаемой специальности. Знач. альтер. призн. обычно задается 0, если объект этим признаком не обладает, и 1 ,если объект этим признаком обладает. Пусть p=m/n тАФ доля единиц совок, обл-х признаком, а q - доля единиц совок, не обл-х этим призн p + q=1. Тогда ср знач. Альтер. призн: Макси знач. дисперсии max=0,25 при р=0,5. Обобщ хар различий внутри ряда служит энтропия распределения. ОПР: Энтропия- мера неопр-сти данных наблюдений. Она зависит от числа проявл-ся признака и от вероятности каждого из них. где рi тАФ вероятности различных знач. случ. величин. Если все варианты равновероятны, то энтропия максимальна.

25. Виды дисперсий

1) Общая дисперсия 2) Межгрупповая дисперсия (Характеризует вариацию изучаемого признака, возникающую под влиянием признака-фактора, положенного в основание группировки) 3) Внутригрупповая дисперсия(отражает часть вариации, происходящей под влиянием неучтенных факторов, которая не зависит от группировочного признака) Средняя из внутригрупповых дисперсий по совокупности в целом - вариация значений признака под влиянием прочих факторов. Правило сложения дисперсий: общая дисперсия, кот возникает под влиянием всех факторов, равна сумме средней из внутригрупповых и межгрупповой

26. .Изучение формы распр-ния.

Процедура выравнивания, сглаживания анализируемого распределения заключается в замене эмпирических частот теоретическими, определяемыми по формуле теоретического распределения, но с учетом фактических значений переменной. На основе сопоставления эмпирических и теоретических частот рассчитываются критерии согласия, которые используются для проверки гипотезы о соответствии исследуемого распределения тому или иному типу теоретических распределении.

Выбор конкретного типа модельного распределения осуществляется исходя из самых общих соображений, опирающихся на визуальный анализ построенных графиков распределения. В практическом анализе обязательной является проверка соответствия изучаемого распределения нормальному закону распределения. Необходимость этого связана с тем, что условием применения значительного числа статистических характеристик и оценок является наличие нормального распределения.

Функция нормального распределения:

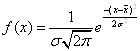плотность нормального распределения:

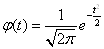где 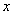ВатАУ значение изучаемого признака, 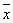- средняя арифметическая величина, 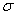- среднее квадратическое отклонение изучаемого признака, e, π тАУ математические константы, 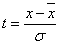ВатАУ нормированное отклонение.

Теоретические частоты нормального отклонения рассчитываются по следующей формуле:

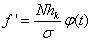где N тАУ объём совокупности, h_k тАУ величина интервала. В моём случае вариационный ряд построен с использованием равных интервалов, следовательно:

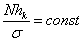Принятие решения о справедливости гипотезы о законе распределения можно осуществить, ориентируясь на эмпирическое значение критерия 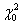, который сравнивается с табличным значением 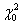. Окончательные выводы по проверке гипотезы о законе распределения: так как 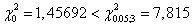, то гипотеза о нормальном распределении регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 г. не противоречит истине.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Аксонометричнi проекцii