Сетевое планирование и управление в менеджменте
Российская Международная Академия Туризма
Курсовая работа
по дисциплине ВлОсновы менеджментаВ»
на тему ВлСетевое планирование и управление в менеджментеВ»
вариант № 9
студентки 206 группы
Бахтеевой Елены Маратовны.
Проверила
Еранцева Елена Михайловна.
г. Химки, микрорайон Сходня 2010 год
Содержание
ВведениеГлава 1. Сетевого планирования и управления
1.1 Сущность сетевого планирования и область его использования
1.2 Элементы сетевой модели
1.3 Правила построения сетевой модели
Глава 2. Расчет параметров и оптимизация сетевой модели
2.1 Исходные данные для построения сетевой модели
2.3 Расчеты характеристик элементов сетевой модели
2.4 Оптимизация сетевой модели
Заключение
Список источников и литературы
Введение
Тема сетевого планирования и управления является актуальной, так как с помощью нее можно научиться строить сетевую модель и при необходимости, оптимизировать ее.
Предметом исследования курсовой работы является сетевое планирование и управление, а объектом - сетевая модель.
Целью курсовой работы является оптимизация сетевой модели, в соответствии с полученным вариантов №9.
Основными задачами данной курсовой работы являются:
1. теоретическое изучение сетевого планирования и у правления, определение его сущности, изучение основных элементов сетевой модели;
2. изучение правил построения модели;
3. расчеты всех параметров сетевой модели, полученной в варианте;
4. оптимизация сетевой модели.
Глава 1. Сетевого планирования и управления
Сетевое планирование и управление (СПУ) тАУ это комплекс графических и расчетных методов, организационных мероприятий, обеспечивающих моделирование, анализ и динамическую перестройку плана выполнения сложных проектов и разработок, например таких как: разработка туристской услуги, исследование системы управления организацией, маркетинговое исследование, разработка стратегий организации и др. Характерной особенностью таких проектов является то, что они состоят из ряда отдельных, элементных работ. Они обусловливают друг друга так, что выполнение некоторых работ не может быть начато раньше, чем завершены некоторые другие. Например, расчет цены услуги нельзя выполнить раньше, чем будет составлена калькуляция; реализация нового тура не может быть осуществлена, если еще не обучен персонал, и т. п.
Сетевое планирование и управление включает три основных этапа: структурное планирование, календарное планирование, оперативное управление.
Структурное сетевое планирование начинается с разбиения проекта на четко определенные операции, для которых определяется продолжительность и необходимые ресурсы. Затем строится сетевая модель (сетевой график), которая представляет взаимосвязи работ проекта. Это позволяет детально анализировать все работы и вносить улучшения в структуру проекта еще до начала его реализации.
Календарное сетевое планирование предусматривает определение моментов времени начала и окончания каждой работы и другие временные характеристики сетевого графика. Это позволяет, в частности, выявлять критические операции и пути сетевой модели, которым необходимо уделять особое внимание, чтобы закончить проект в директивный срок. Во время календарного планирования определяются все временные характеристики всех работ и событий с целью оптимизациисетевой модели, которая позволит улучшить эффективность использования какого-либо ресурса (трудовых ресурсов, времени, денежных средств и др.).
В ходе оперативного сетевого управления используются оптимизированный сетевой график и календарные сроки для составления периодических отчетов о ходе выполнения проекта. При этом модель может подвергаться оперативной корректировке, вследствие чего будет разрабатываться новые параметры остальной части сетевой модели.
Сетевая модель тАУ это план выполнения некоторого комплекса взаимосвязанных работ, заданного в форме сети, графическое изображение которой называется сетевым графиком. Математический аппарат сетевых моделей базируется на теории графов.
Графом называется совокупность двух конечных множеств: тАУ множества точек, которые называются вершинами, и множества связей между парами вершин, которые называются ребрами. Если рассматриваемые пары вершин являются упорядоченными, т. е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае тАУ неориентированным. Последовательность повторяющихся ребер, ведущая от некоторой вершины к другой, образует путь. Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным. В экономике и управлении чаще всего используется два вида графов: дерево и сеть.
Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями.
Сеть тАУ это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину (сток). Таким образом, сетевая модель представляет собой граф вида ВлсетьВ».
Объектом управления в системах сетевого планирования и управления являются коллективы исполнителей, располагающие определенными ресурсами и выполняющие комплекс операций, который призван обеспечить достижение намеченной цели, например разработку новой услуги тАУ исследование системы управления, реализацию комплекса управленческих процедур и операций для достижения стратегической организации и др.
Элементами сетевой модели являются: работы, события, пути.
Работа тАУ это либо любой активный трудовой процесс, требующий затрат времени и ресурсов и приводящий к достижению определенных результатов (событий), либо пассивный процесс (ВложиданиеВ»), не требующий затрат труда, но занимающий время, либо, наконец, связь между какими-то результатами работ (событиями), называемая фиктивной работой. Обычно действительные работы в сетевом графике обозначаются сплошными стрелками, а фиктивные работы тАУ пунктирными.
СобытиетАУ это итог проведенных работ, который дает начало для дальнейших (последующих) работ. Событие не имеет продолжительности во времени. Событие, за которым начинается данная работа, называется начальным для данной работы; оно обозначается символом i. Событие, которое наступает после выполнения данной работы, называется конечным для данной работы; оно обозначается символом j.
В каждой сети имеются два крайних события тАУ исходное и завершающее. Исходным называется событие в сети, не имеющее предшествующих событий и отражающее начало выполнения всего комплекса работ. Оно обозначается символом I. Завершающим называется событие, которое не имеет последующих событий и показывает достижение конечной цели выполнения комплекса работ. Оно обозначается символом К. В одно и то же событие может входить и выходить из него несколько видов работ.
Путь тАУ это любая последовательность работ в сетевом графике, в котором конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Если известна продолжительность каждой работы tij, то для каждого пути может быть вычислена его общее время выполнения тАУ длина, т. е. общая сумма продолжительности всех работ пути ТLi.
В сетевом графике следует различать несколько видов путей:
v полный путь тАУ путь от исходного события до завершающего;
v полный путь с максимальной продолжительностью называется критическим путемLкр;
v путь, предшествующий данному событию, тАУ путь от исходного события до данного;
v путь, следующий за данным событием, тАУ путь от данного события до завершающего;
v путь между событиями i и j;
v подкритический путь тАУ полный путь, ближайший по длительности к критическому пути;
v ненагруженный путь тАУ полный путь, длительность которого значительно меньше длительности критического пути.
Правило 1.Сеть имеет только одно начальное событие и только одно конечное событие.
Правило 2.Сеть вычерчивается слева направо. Желательно, чтобы каждое событие с большим порядковым номером изображалось правее предыдущего. Для каждой работы (iтАУj) должно выполняться iОбщее направление стрелок, изображающих работы, также должно быть расположено слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером. Изображение и обозначение работ и событий представлены на рис.1.
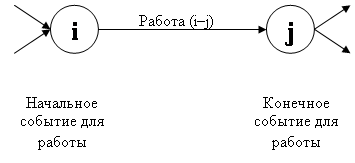
Рис.1. Изображение и обозначение работ и событий
Правило 3.Если в процессе выполнения работы начинается другая работа, использующая результат некоторой части первой работы, то первая работа разбивается на две: причем часть первой работы от начала (0) до выдачи промежуточного результата, т. е. начало второй работы и оставшаяся часть первой работы, выделяются как самостоятельные.
Правило 4. Если ВлnВ» работ начинаются и кончаются одними и теми же событиями, то для установления взаимно-однозначного соответствия между этими работами и кодами необходимо ввести (n-1) фиктивных работ. Они не имеют продолжительности во времени и вводятся в данном случае лишь для того, чтобы упомянутые работы имели разные коды.
Правило 5. В сети не должно быть событий, в которые не входит ни одной работы, кроме исходного события. Нарушение этого правила и появление в сети, кроме исходного, еще одного события, в которое не входит ни одной работы, означает либо ошибку при построении сетевого графика, либо отсутствие (непланирование) работы, результат которой необходим для начала работы.
Правило 6. В сети не должно быть событий, из которых не выходит ни одной работы, кроме завершающего события. Нарушение этого правила и появление в сети, кроме завершающего, еще одного события, из которого не выходит ни одной работы, означает либо ошибку при построении сетевого графика, либо планирование ненужной работы, результат которой никого не интересует.
Правило 7. События следует нумеровать так, чтобы номер начального события данной работы был меньше номера конечного события этой работы.
Правило 8. В цепи не должно быть замкнутого контура. Построение сети является лишь первым шагом на пути к построению календарного плана. Вторым шагом является расчет сетевой модели, который выполняют на сетевом графике, пользуясь простыми правилами и формулами, или используют математическое представление сетевой модели в виде системы уравнений, целевой функции и граничных условий. Третий шаг тАУ оптимизация модели.
Глава 2. Расчет параметров и оптимизация сетевой модели
Таблица 1. Исходные данные для построения сетевой модели.
| № | Обозначение работы i-j | Q i-j | W i-j | № | Обозначение работы i-j | Q i-j | W i-j |
1 2 3 4 5 6 7 8 9 10 | 0 тАУ 1 0 тАУ 2 0 тАУ 3 0 тАУ 4 1 тАУ 5 1 тАУ 6 2 тАУ 7 3 тАУ 7 4 тАУ 8 4 тАУ 9 | 30 60 20 14 12 8 0 12 30 6 | 7 2 5 4 3 4 0 6 7 2 | 11 12 13 14 15 16 17 18 19 20 | 5 тАУ 10 5 тАУ 13 6 тАУ 11 7 тАУ 11 8 тАУ 3 9 тАУ 12 10 тАУ 13 11 тАУ 13 12 тАУ 14 13 тАУ 14 | 12 16 30 20 0 20 16 20 8 10 | 3 4 1 1 0 5 4 1 2 1 |
Расчет продолжительности каждой работы в человеко-днях по формуле:
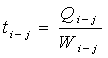
t0 - 1 = 30:7=4,3
t0 тАУ 2 = 60:2=30
t0 тАУ 3 = 20:5=4
t0 тАУ 4 = 14:4=3,5
t1 тАУ 5 = 12:3=4
t1 тАУ 6 = 8:4=2
t2 тАУ 7 = 0 : 0 = 0
t3 тАУ 7 = 12:6=2
t4 тАУ 8 = 30:7=4,3
t4 тАУ 9 = 6:2=3
t5 тАУ 10 = 12:3=4
t5 тАУ 13 = 16:4=4
t6 тАУ 11 = 30:1=30
t7 тАУ 11 = 20:1=20
t8 тАУ 3 = 0 : 0 = 0
t9 тАУ 12 = 20:5=4
t10 -13 = 16:4=4
t11 -13 = 20:1=20
t12 -14 = 8:2=4
t13 тАУ 14 = 10:1=10
Вместе с этим смотрят:
Cамоорганизация как процесс саморазвития
РЖнновацiйнi процеси на пiдприiмствi
РЖнтуiцiя в бiзнесi
РЖнформацiйний менеджмент як ефективна технологiя органiзацii управлiнськоi дiяльностi
Аксiологiчнi проблеми управлiнськоi дiяльностi робiтника освiти в умовах модернiзацii освiтньоi галузi в Украiнi