Теория остатков

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

ВлГомельский государственный университет

имени Франциска Скорины В»

Математический факультет

Кафедра алгебры и геометрии

Допущена к защите

Зав. кафедрой _________ Шеметков Л.А.

Вл_____В» ____________ 2006 г.

ТЕОРИЯ ОСТАТКОВ

ДИПЛОМНАЯ РАБОТА

Исполнитель:

студентка группы М-52 ____________ Клименко Ю.

Научный руководитель:

к.ф-м.н., доцент кафедры

алгебры и геометрии ____________ Подгорная В.

Рецензент:

ст. преподаватель

кафедры высшей

математики ____________ Курносенко Н.

Гомель 2008

Содержание

Введение. 3

1 Алгоритм Евклида. 4

1.1 Определения алгоритма. 4

1.2 Алгоритм Евклида. 5

1.3 Применения алгоритма Евклида. 12

2 Делимость в кольцах. 17

2.1 Область целостности. 17

2.2 Кольцо частных. 19

2.3 Евклидовы кольца. 21

3 Сравнения и арифметика остатков. 27

4 Функция Эйлера. 41

5 Китайская теорема об остатках. 53

Заключение. 62

Список использованных источников. 63

Введение

История арифметики остатков начинается с исследований К.Ф. Гаусса, который впервые стал рассматривать сравнения. В дальнейшем была обнаружена связь теории сравнений с астрономическими задачами (китайская теорема об остатках). В результате многочисленных исследований теория остатков была распространена на кольца произвольной природы. В последнее время обнаружилось приложение этой теории в криптографии. В дипломной работе изложена теория остатков на современном алгебраическом языке.

Дипломная работа состоит из пяти разделов.

В первом разделе изложено понятие остатка, наибольшего общего делителя, алгоритма Евклида, расширенного алгоритма Евклида и применение алгоритма Евклида для решения линейных диофантовых уравнений и разложение чисел в цепные дроби.

Во втором разделе изложен алгебраический подход к делимости в кольцах. Рассмотрена область целостности, кольцо частных и евклидовы кольца.

В третьем разделе изложены теории вычетов по модулю и теория сравнений. Приведено применении теории остатков в криптографии (алгоритм RSA).

В четвертом разделе изложена теория мультипликативных функция и подробно рассмотрена функция Эйлера, с её свойствами.

В пятом разделе изложена китайская теорема об остатках для колец.

1 Алгоритм Евклида

1.1 Определения алгоритма

Единого ВлистинногоВ» определения понятия ВлалгоритмВ» нет.

ВлАлгоритм тАФ это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.В» (А. Колмогоров)

ВлАлгоритм тАФ это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.В» (А. Марков)

ВлАлгоритм есть формализованная последовательность действий (событий). Алгоритм может быть записан словами и изображен схематически. Практически любое неслучайное повторяемое действие поддается описанию через алгоритм.В»

ВлАлгоритм тАФ это система операторов, взятых из множества операторов некоторого исполнителя, которая полностью определяет некоторый класс алгоритмических процессов, то есть процессов, которые:

1. дискретны;

2. детерминированы;

3. потенциально конечны;

4. преобразовывают некоторые конструктивные объекты.

Между операторами алгоритма и операциями (элементарными действиями) алгоритмического процесса существует гомоморфное соответствие. Поэтому алгоритм следует также считать моделью алгоритмического процессаВ». (А. Копаев)

Формальные признаки алгоритмов

Различные определения алгоритма в явной или неявной форме содержат следующий ряд общих требований:

В· детерминированность тАФ определённость. В каждый момент времени следующий шаг работы однозначно определяется состоянием системы. Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных. В современной трактовке у разных реализаций одного и того же алгоритма должен быть изоморфный граф. С другой стороны, существуют вероятностные алгоритмы, в которых следующий шаг работы зависит от текущего состояния системы и генерируемого случайного числа.

В· понятность тАФ алгоритм для исполнителя должен включать только те команды, которые ему (исполнителю) доступны, которые входят в его систему команд.

В· завершаемость (конечность) тАФ при корректно заданных исходных данных алгоритм должен завершать работу и выдавать результат за конечное число шагов. С другой стороны, вероятностный алгоритм может и никогда не выдать результат, но вероятность этого равна 0.

В· массовость тАФ алгоритм должен быть применим к разным наборам исходных данных.

Современное формальное определение алгоритма было дано в 30-50-х гг. XX века в работах Тьюринга, Поста, Чёрча (тезис Чёрча тАФ Тьюринга), Н. Винера, А. А. Маркова.

1.2 Алгоритм Евклида

Определение. Число d Z , делящее одновременно числа а , , c , .. , k Z , называется общим делителем этих чисел. Наибольшее d с таким свойством называется наибольшим общим делителем. Обозначение: d = ( a , , c , .., k ) .

Теорема. Если ( a , ) = d , то найдутся такие целые числа u и v , что d = au + bv .

Доказательство. Рассмотрим множество P = { au + bv u,v Z }. Очевидно, что P Z , а знатоки алгебры могут проверить, что P тАУ идеал в Z . Очевидно, что a , , 0 P . Пусть x , y P и y 0 . Тогда остаток от деления x на y принадлежит P . Действительно:

x = yq + r , 0 r < y ,

r = x тАУ yq = ( au ₁ + bv ₁ ) тАУ ( au ₂ + bv ₂ ) q = a ( u ₁ тАУ u ₂ q )+ ( v ₁ тАУ v ₂ q ) P .

Пусть d P - наименьшее положительное число из P (призадумайтесь, почему такое имеется!). Тогда а делится на d . В самом деле, a = dq + r ₁ , 0 r ₁ < d , a P , d P , значит r ₁ P , следовательно r ₁ = 0. Аналогичными рассуждениями получается, что делится на d , значит d - общий делитель a и .

Далее, раз d P , то d = au ₀ + bv ₀ . Если теперь d ₁ - общий делитель a и , то d ₁ | ( au ₀ + bv ₀ ), т.е. d ₁ | d . Значит d d ₁ и d - наибольший общий делитель.

Определение. Целые числа a и называются взаимно простыми, если (a , ) = 1.

Вспоминая свойство 1 из предыдущего пункта, легко заметить, что два числа a и являются взаимно простыми тогда и только тогда, когда найдутся целые числа u и v такие, что au + bv = 1.

Пусть даны два числа a и ; a 0, 0, считаем, что a > . Символом := в записи алгоритма обозначаем присваивание. Алгоритм:

1. Ввести a и .

2. Если = 0 , то Ответ: а . Конец .

3. Заменить r := "остаток от деления а на ", а := , := r .

4. Идти на 2.

В современной буквенной записи, алгоритм Евклида выглядит так: a > b; a, b Z .

Имеем: > r ₁ > r ₂ >.. > r _n > 0, следовательно процесс оборвется максимум через шагов. Очень интересный и практически важный народохозяйственный вопрос о том, когда алгоритм Евклида работает особенно долго, а когда справляется с работой молниеносно, мы рассмотрим чуть позже. Давайте сейчас покажем, что r _n = ( a , ). Просмотрим последовательно равенства сверху вниз: всякий делитель а и делит r ₁ , r ₂ ,.., r _n . Если же просматривать эту цепочку равенств от последнего к первому, то видно, что r _n | r _{n -1} , r _n | r _{n -2} , и т.д., т.е. r _n делит а и . Поэтому r _n - наибольший общий делитель чисел а и .

Как и всякая добротно выполненная работа, алгоритм Евклида дает гораздо больше, чем от него первоначально ожидалось получить. Из его разглядывания ясно, например, что совокупность делителей а и совпадает с совокупностью делителей ( a , ). Еще он дает практический способ нахождения чисел u и v из Z (или, если угодно, из теоремы пункта 2) таких, что r _n = au + bv = ( a, b ).

Действительно, из цепочки равенств имеем:

r _n = r _{n -2} - r _{n -1} q _n = r _{n -2} - ( r _{n -3} - r _{n -2} q _{n -1} ) q _n = ..

(идем по цепочке равенств снизу вверх, выражая из каждого следующего равенства остаток и подставляя его в получившееся уже к этому моменту выражение)

.. = au + bv = ( a , ).

Пример. Пусть а = 525, = 231. (ниже приводится запись деления уголком, и каждый раз то, что было в уголке, т.е. делитель, приписывается к остатку от деления с левой стороны, а остаток, как новый делитель, берется в уголок)

Запись того же самого в виде цепочки равенств:

525 = 231 В· 2 + 63

231 = 63 В· 3 + 42

63 = 42 В· 1 + 21

42 = 21 В· 2

Таким образом, (525, 231) = 21. Линейное представление наибольшего общего делителя:

21 = 63 - 42 В· 1 = 63 - (231 - 63 В· 3) В· 1 =

= 525 - 231 В· 2 - (231 - (525 - 231 В· 2) В· 3) =

= 525 В· 4 - 231 В· 9,

и наши пресловутые u и v из Z равны, соответственно, 4 и - 9.

Приступим теперь к исполнению второй части названия этого пункта - анализу алгоритма Евклида. Нас будет интересовать наихудший случай - когда алгоритм работает особенно долго? Спросим точнее: какие два наименьших числа надо засунуть в алгоритм Евклида, чтобы он работал в точности заданное число шагов? Ответ на этот вопрос дает

Теорема (Ламэ, 1845 г.). Пусть n N , и пусть a > b > 0 такие, что алгоритму Евклида для обработки а и b необходимо выполнить точно n шагов (делений с остатком), причем а - наименьшее с таким свойством. Тогда а = _{n +2} , b = _{n +1} , где _k - k- ое число Фибоначчи.

Следствие. Если натуральные числа a и не превосходят N N , то число шагов (операций деления с остатком), необходимых алгоритму Евклида для обработки a и не превышает log _Ф ( 5 N ) - 2, где - верхнее целое , = (1 + 5)/2 - больший корень характеристического уравнения последовательности Фибоначчи.

Доказательство. Максимальное число шагов достигается при а = _n+2 , = _{n +1} , где - наибольший номер такой, что _{n +2} < N . Рассматривая формулу для -ого члена последовательности Фибоначчи, легко понять, что _{n +2} - ближайшее целое к (1/ 5) ^{n +2} . Значит (1/ 5) ^{n +2} < N , следовательно, +2 < log _Ф ( 5 N ), откуда моментально даже < log _Ф ( 5 N ) - 3 (именно "минус три", ведь рассматривается верхнее целое).

log _Ф ( 5 N ) 4,785 В· lg N + 1,672, поэтому, например, с любой парой чисел, меньших миллиона, алгоритм Евклида разбирается не более, чем за 4,785 В· 6 + 1,672 - 3 = 31 - 3 = 28 шагов.

Листинг алгоритма Евклида на языке С

// Обобщенный алгоритм Евклида для поиска наибольшего общего

// делителя gcd = НОД(u,v) целых положительных чисел u и v

// и коэффициентов a и b уравнения a*u + b*v = gcd

// Все числа полагаются типа long

// Подстановки упрощающие запись исходного текста

#define isEven(x) ((x & 0x01L) == 0)ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа // x - четное?

#define isOdd(x) ((x & 0x01L))ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа // x - нечетное?

#define swap(x,y) (x ^= y, y ^= x, x ^= y) // обмен значений x и y

void GenEuclid(long *u, long *v, long *a, long *b, long *gcd)

{

int k; ВаВаВаВаВа // Параметр циклов

long a1, b1, g1; Ва // Вспомогательные переменные

// Алгоритм предполагает, что u > v, если u < v, то они переставляются

if (*u < *v) swap(*u, *v);

// Если u = n * 2^k1 или v = m * 2^k2, то перед поиском НОД

// производим сокращение u = u/(2^k), v = v/(2^k),

// где k - минимальное из k1, k2. Показатель k запоминаем.

for (k = 0; isEven(*u) && isEven(*v); ++k){

ВаВа *u >>= 1; *v >>= 1;

}

// Задание начальных значений

*a = 1; *b = 0; *gcd = *u; a1 = *v; b1 = *u - 1; g1 = *v;

do {

ВаВа do {

ВаВаВаВаВаВаВаВаВаВаВаВаВаВа if (isEven(*gcd)){

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа if (isOdd(*a) || isOdd(*b)){

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа *a += *v; *b += *u;

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа }

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа *a >>= 1; *b >>= 1; *gcd >>= 1;

ВаВаВаВаВаВаВаВаВаВаВаВаВаВа }

ВаВаВаВаВаВаВаВаВаВаВаВаВаВа if (isEven(g1) || *gcd < g1){

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа swap(*a, a1); swap(*b, b1); swap(*gcd, g1);

ВаВаВаВаВаВаВаВаВаВаВаВаВаВа }

ВаВа } while (isEven(*gcd));

ВаВа while(*a < a1 || *b < b1){

ВаВаВаВаВаВаВаВаВаВаВаВаВаВа *a += *v; *b += *u;

ВаВа }

ВаВа *a -= a1; *b -= b1; *gcd -= g1;

} while (g1 > 0);

while (*a >= *v && *b >= *u){

ВаВа *a -= *v; *b -= *u;

}

// производим умножение коэффициентов уравнения

// на сокращенный ранее множитель 2^k

*a <<= k; *b <<= k; *gcd <<= k;

}

Расширенный алгоритм Евклида и соотношение Безу

Формулы для r_i могут быть переписаны следующим образом:

r₁ = a + ( - q₀)

r₂ = − r₁q₁ = a( − q₁) + (1 + q₁q₀)

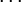
(a,) = r_n = as + bt

здесь и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа и t тАФ коэффициентами Безу. Соотношение Безу является ключевым в доказательстве основной теоремы арифметики.

1.3 Применения алгоритма Евклида

Пусть требуется решить линейное диофантово уравнение:

ax + by = c ,

где a , , c Z ; a и - не нули.

Попробуем порассуждать, глядя на это уравнение.

Пусть ( a , ) = d . Тогда a = a ₁ d ; = ₁ d и уравнение выглядит так:

a ₁ dВ· x + ₁ dВ· y = c , т.е. dВ· ( a ₁ x + ₁ y ) = c .

Теперь ясно, что у такого уравнения имеется решение (пара целых чисел x и y ) только тогда, когда d | c . Пусть d | c . Поделим обе части уравнения на d , и всюду далее будем считать, что ( a , ) = 1.

Рассмотрим несколько случаев.

Случай 1. Пусть c = 0, уравнение имеет вид ax + by = 0 - " однородное линейное диофантово уравнение".