Транспортная задача линейного программирования

Международный университет

Калининградский филиал

Заочное отделение

Специальность-менеджмент

Курсовая работа

по дисциплине экономикотАУматематические методы

Транспортная задача

линейного программирования

КурсоваяВа работа

ВапоВа высшейВа математике

Тема:

тАЭТранспортная задача линейного программированиятАЭ

Содержание:

1. История зарождения и создания линейного программирования.

2. Транспортная задача. Общая постановка, цели, задачи. Основные типы, виды моделей.

3. Методы составления начального опорного плана.

4. Понятие потенциала и цикла.

5. Критерий оптимальности базисного решения транспортной задачи. Методы отыскания оптимального решения.

6. Задача, двойственная к транспортной.

7. Пример решения транспортной задачи.

8. Выводы.

1.История зарождения и создания линейного программирования.

Каждый человек ежедневно, не всегда осознавая это, решает проблему: как получить наибольший эффект, обладая ограниченными средствами. Наши средства и ресурсы всегда ограничены. Жизнь была бы менее интересной, если бы это было не так. Не трудно выиграть сражение, имея армию в 10 раз большую, чем у противника. Чтобы достичь наибольшего эффекта, имея ограниченные средства, надо составить план, или программу действий. Раньше план в таких случаях составлялся тАЬна глазоктАЭ (теперь, впрочем, зачастую тоже). В середине XX века был создан специальный математический аппарат, помогающий это делать тАЬпо наукетАЭ. Соответствующий раздел математики называется математическим программированием. Слово тАЬпрограммированиетАЭ здесь и в аналогичных терминах (тАЬлинейное программирование, динамическое программированиетАЭ и т.п.) обязано отчасти историческому недоразумению, отчасти неточному переводу с английского. По-русски лучше было бы употребить слово тАЬпланированиетАЭ. С программированием для ЭВМ математическое программирование имеет лишь то общее, что большинство возникающих на практике задач математического программирования слишком громоздки для ручного счета, решить их можно только с помощью ЭВМ, предварительно составив программу. Временем рождения линейного программирования принято считать 1939г., когда была напечатана брошюра Леонида Витальевича Канторовича тАЬМатематические методы организации и планирования производстватАЭ. Поскольку методы, изложенные Л.В.Канторовичем, были мало пригодны для ручного счета, а быстродействующих вычислительных машин в то время не существовало, работа Л.В.Канторовича осталась почти не замеченной.

ВаВаВаВаВаВаВаВаВаВа Свое второе рождение линейное программирование получило в начале пятидесятых годов с появлением ЭВМ. Тогда началось всеобщее увлечение линейным программированием, вызвавшее в свою очередь развитие других разделов математического программирования. В 1975 году академик Л.В.Канторович и американец профессор Т.Купманс получили Нобелевскую премию по экономическим наукам за тАЬвклад в разработку теории и оптимального использования ресурсов в экономикетАЭ.

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа В автобиографии, представленной в Нобелевский комитет, Леонид Витальевич Канторович рассказывает о событиях, случившихся в 1939 году. К нему, 26-летнему профессору-математику, обратились за консультацией сотрудники лаборатории планерного треста, которым нужно было решить задачу о наиболее выгодном распределении материала между станками. Эта задача сводилась к нахождению максимума линейной функции, заданной на многограннике. Максимум такой функции достигался в вершине, однако число вершин в этой задаче достигало миллиарда. Поэтому простой перебор вершин не годился. Леонид Витальевич писал: тАЬоказалось, что эта задача не является случайной. Я обнаружил большое число разнообразных по содержанию задач, имеющих аналогичный математический характер: наилучшее использование посевных площадей, выбор загрузки оборудования, рациональный раскрой материала, распределение транспортных грузопотоковтАж Это настойчиво побудило меня к поиску эффективного метода их решениятАЭ. И уже летом 1939 года была сдана в набор книга Л.В.Канторовича тАЬМатематические методы организации и планирования производстватАЭ, в которой закладывались основания того, что ныне называется математической экономикой.

ВаВаВаВаВаВаВаВаВаВа Однако идеи Л.В.Канторовича не встретили понимания в момент их зарождения, были объявлены ересью, и его работа была прервана. Концепции Леонида Витальевича вскоре после войны были переоткрыты на западе. Американский экономист Т.Купманс в течение многих лет привлекал внимание математиков к ряду задач, связанных с военной тематикой. Он активно способствовал тому, чтобы был организован математический коллектив для разработки этих проблем. В итоге было осознано, что надо научиться решать задачи о нахождении экстремумов линейных функций на многогранниках, задаваемых линейными неравенствами. По предложению Купманса этот раздел математики получил название линейного программирования.

ВаВаВаВаВаВаВаВа Американский математик А.Данциг в 1947 году разработалВа весьма эффективный конкретный метод численного решения задач линейного программирования (он получил название симплекс метода). Идеи линейного программирования в течение пяти шести лет получили грандиозное распространение в мире, и имена Купманса и Данцига стали повсюду широко известны.

ВаВаВаВаВаВаВа Примерно в это время Купманс узнал, что еще до войны в далекой России уже было сделано нечто похожее на разработку начал линейного программирования. Как легко было бы Данцигу и Купмансу проигнорировать эту информацию! Маленькая книжица, изданная ничтожным тиражом, обращенная даже не к экономистам, а к организаторам производства, с минимумом математики, без четко описанных алгоритмов, без доказательств теорем тАУ словом, стоит ли принимать такую книжку во вниманиетАж Но Купманс настаивает на переводе и издании на западе книги Канторовича. Его имя и идеи становятся известны всем. Воздадим должное благородству американского ученого!

ВаВаВаВаВаВаВаВаВа А самому Леониду Витальевичу тАУ как естественно было бы ему, испытав первые грозные удары ретроградов, остеречься от тАЬгреховтАЭ молодости, забыть про всю эту экономику и вернуться к математике. Но Л.В.Канторович продолжает писать математические работы, навеянные экономическими идеями, участвует и в конкретных разработках на производстве. При этом (одновременно с Данцигом, но, не зная его работ) он разрабатывает метод, позже названный симплекс-методом. Как только в 50-е годы образуется маленький просвет, и кое-что из запретного становитсяВа возможным, он организуетВа группу студентов на экономическом факультете ЛГУ для обучения методам оптимального планирования. А, начиная с 1960 года, Леонид Витальевич занимается только экономической и связанной с нею математической проблемами. Его вклад в этой области был отмечен Ленинской премией в 1965 году (присуждена ему совместно с В.С.Немчиновым и В.В.Новожиловым) и, как уже говорилось, Нобелевской премией в 1975 году.

2.Транспортная задача. Общая постановка, цели, задачи. Основные типы, виды моделей.

Под названием тАЬтранспортная задачатАЭ объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.

В общей постановке транспортная задача состоит в отыскании оптиВнмального плана перевозок некоторого однородного груза с 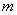баз 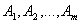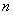Вапотребителям .

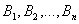Различают два типа транспортных задач: но критерию стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию) и по критерию времени (план оптимален, если на его реализацию затрачивается минимум времени).