Способи перетворення креслення
Житомирський Вiйськовий РЖнститут
Нацiонального Авiацiйного Унiврситету
Реферат
на тему:
Способи перетворення креслення
Житомир 2010
Задачi нарисноi геометрii можна роздiлити на позицiйнi та метричнi.
В метричних задачах треба знайти натуральнi розмiри геометричних фiгур, якi данi на кресленнi своiми проекцiями в загальному видi. Наприклад, знайти довжину вiдрiзка, величину кута та iн. Подiбну задачу вирiшили на практичному заняттi № 2 тАУ визначали натуральну величину вiдрiзка прямоi та кут нахилу до площини проекцii.
В позицiйних задачах треба знайти положення геометричних фiгур (точки, прямоi, площини, фiгури), якi задовольняють умовам задачi. Наприклад, знайти точку перетину прямоi з площиною, провести пряму або площину через дану точку, знайти лiнiю перетину площин i т. iн. Таку задачу вирiшили на практичному заняттi № 3.
РозвтАЩязування просторових задач на комплексному кресленнi значно спрощуiться, якщо елементи простору, якi нас цiкавлять, займають частинне положення, тобто розташованi паралельно або перпендикулярно площинам проекцiй. Це перш за все стосуiться прямих лiнiй, площин, гранних i криволiнiйних поверхонь. Пiсля перетворення комплексного креслення одержанi проекцii дають можливiсть значно спростити хiд розвтАЩязування задачi.
Щоб досягти частинного розташування геометричних фiгур, комплексне креслення перетворюють або перебудовують, виходячи з конкретних умов.
РЖснують два основних способи перетворення проекцiй:
1) спосiб замiни площин проекцiй;
2) спосiб обертання.
При першому способi положення фiгури вiдносно площин проекцiй залишаiться незмiнним, змiнюiться тiльки положення одноi з площин проекцiй, причому площина, яку замiнюють залишаiться в положеннi перпендикулярному до незмiнюваноi площини.
В другому способi обертання положення площин проекцiй залишаiться незмiнним, змiнюiться положення фiгури вiдносно площин проекцiй шляхом обертання ii навколо осi, паралельноi одноi з площин проекцiй.
Оскiльки частинних положень у прямоi два i в площини два, то iснують чотири задачi для перетворення комплексного креслення:
1) пряму загального положення зробити прямою рiвня;
2) пряму рiвня зробити проекцiюючою прямою;
3) площину загального положення зробити проекцiюючою;
4) проекцiюючу площину зробити площиною рiвня.
1. Спосiб замiни площин проекцiй
Теорiя способу замiни площин. Суть цього способу полягаi в тому, що просторове положення заданих елементiв або фiгури залишаiться незмiнним, а змiнюiться система площин проекцiй. Додатковi площини проекцiй вводяться так, щоб на них елементи, якi нас цiкавлять, зображувалися в зручному для конкретноi задачi положеннi. Тобто одна з основних площин р2 або р1 замiняiться новою додатковою площиною р4, розташованою паралельно або перпендикулярно заданiй геометричнiй фiгурi. Перетворення проекцiй деякоi геометричноi фiгури, яке здiйснюiться способом замiни площин, проекцiй, повтАЩязане з перетворенням проекцiй точок, що належать данiй фiгурi. Тому розглянемо спочатку, яких змiн зазнають проекцii окремоi точки при переходi вiд однiii системи ортогональних площин до iншоi.
На рис. 1 точка A задана в системi р2/ р1. Вiсь проекцiй будемо позначати записом в виглядi дробу тАУ позначення площин представляють собою як би чисельник та знаменник, причому кожна буква ставиться по той бiк вiсi, де повиннi розмiщуватися вiдповiднi проекцii. Площина р2 замiнена новою площиною р4 перпендикулярною до р1. Площина р1 i загальною в системi р2/р1 i р1/р4, то координата zA залишаiться незмiнною.
Отже, вiдстань вiд новоi фронтальноi проекцii до новоi вiсi x14 дорiвнюi вiдстанi вiд замiнюваноi проекцii до вiсi x12.
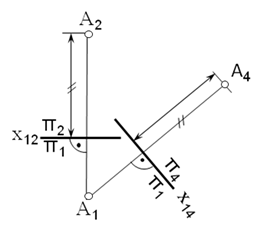
Рис. 1
Для одержання епюра точки А площину р4 обертають навколо вiсi x14 до сполучення з площиною р1. Сумiститься з р4 i нова фронтальна проекцiя А4 точки А, яка виявиться на спiльному перпендикулярi до новоi вiсi х14 з горизонтальною проекцiiю А1, яка не змiнила свого положення (рис. 2)
Аналогiчно можна замiнити горизонтальну площину проекцiй р1 площиною р4, також перпендикулярною р2 (рис. 3,а). У цьому випадку величина координати у, котра визначаi вiдстань вiд точки В до спiльноi для двох систем площини р2, не змiниться. Тому вiдстань вiд новоi ВлгоризонтальноiВ» проекцii точки до новоi осi х24 дорiвнюi вiдстанi вiд точки В1 до осi х12.
При побудовi новоi проекцii точки на епюрi (рис. 3,б) iз В2 опускають перпендикуляр на нову вiсь х24, на якому вiд отриманоi точки вiдкладають вiдрiзок, що дорiвнюi координатi у.
Висновки:
тАУ при замiнi фронтальноi площини проекцiй р2 новою площиною горизонтальна проекцiя точки залишаiться без змiн;
тАУ щоб визначити нову фронтальну проекцiю точки, треба з горизонтальноi проекцii опустити перпендикуляр на нову вiсь i вiд вiсi вiдкласти на ньому вiдрiзок, який дорiвнюi вiдстанi вiд замiнюваноi проекцii до староi осi, тобто координату z даноi точки.
Деякi перетворення проекцiй вимагають подвiйноi замiни площин. Послiдовний перехiд вiд однiii системи площин проекцiй до iншоi необхiдно здiйснювати, дотримуючись такого правила: вiдстань вiд новоi проекцii точки до новоi осi маi дорiвнювати вiдстанi вiд перетворюваноi (замiнюваноi) проекцii точки до попередньоi осi.
Для розумiння та просторового уявлення переходу вiд одноi системи площин до 2 iнших розглянемо декiлька задач.
Задача 3. Перетворити креслення так, щоб площина загального положення в новiй системi площин проекцiй стала проекцiюючою.
Нехай площина загального положення задана трьома точками А, В, С (рис. 4). Для розвтАЩязування сформульованоi задачi нову площину проекцiй потрiбно розташувати перпендикулярно трикутнику ABC i однiй з площин проекцiй. Нова площина маi бути перпендикулярна лiнii перетину заданоi площини з однiiю з площин проекцiй. При цьому немаi необхiдностi будувати таку лiнiю, оскiльки ii напрям можна встановити за допомогою головноi лiнii площини.
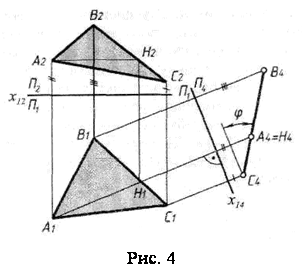
Ось чому в заданiй площинi перш за все проводять одну з головних лiнiй, наприклад горизонталь АН. Ця горизонталь потрiбна для орiiнтування новоi площин проекцiй р 4.
Розташувавши р4 ^ АН, ми забезпечуiмо виконання двох умов одразу: нова площина р4 буде перпендикулярна i до р1 i до площини трикутника. Нову вiсь х24 проводять пiд прямим кутом до А1Н1. Провiвши через горизонтальнi проекцii вершин трикутника прямi, перпендикулярнi до новоi осi, вiдкладають на них вiд х14 вiдрiзки, що дорiвнюють zA, zB i zС. Так одержують нову фронтальну проекцiю А4В4С4 трикутника ABC, яка являi собою пряму лiнiю. Вiдмiтимо, що на площину р4, яка перпендикулярна до трикутника i р1, без спотворення проекцiюiться кут ц, утворений трикутником з площиною р1 .
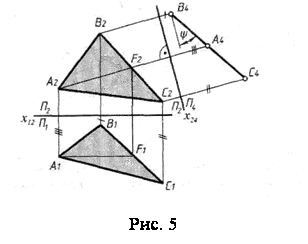
Аналогiчне перетворення виконано на рис. 5, де площина р1 замiнена площиною р4, перпендикулярною до р2 i трикутника ABC. Для цього в площинi трикутника була проведена фронталь AF, перпендикулярно до якоi i розташовуiться площина р4. Нова вiсь х24 вибрана перпендикулярно до A2F2. Площина трикутника вiдносно р1 стала проекцiюючою. На площину р4 без спотворення проекцiюiться кут y нахилу трикутника до фронтальноi площини проекцiй р2.
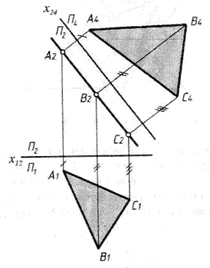
Задача 4. Перетворити креслення так, щоб площина загального положення стала паралельною однiй з площин проекцiй новоi системи
Нехай задано трикутник ABC у площинi загального положення (рис. 6). Потрiбно створити таку нову ортогональну систему площин проекцiй, в якiй одна з них маi бути паралельною трикутнику. В системi р2/ р1 таку площину побудувати не можна. Справдi, площина трикутника, не буде перпендикулярна нi до р1 нi до р2 , тобто вона не утворюi з площинами проекцiй ортогональноi системи.
РозвтАЩязування задачi потребуi подвiйноi замiни площин проекцiй. Суть першоi замiни р2 на р4 полягаi в перетвореннi площини трикутника в проекцiюючу площину. Цей процес описаний вище задачi № 3.
Другий етап розвтАЩязування задачi полягаi в переходi вiд системи р1/ р4 до системи р4/ р5. Нова площина р5 установлюiться паралельно трикутнику, а отже, нова вiсь х45 на епюрi проводиться паралельно прямiй, на якiй виявились розташованими точки А4, В4 i С4. Як правило, через вказанi точки проводять перпендикуляри до новоi осi i вiдкладають на них вiд х45 вiдрiзки, що дорiвнюють lА, lв, lс. Побудована проекцiя А5В5С5 визначаi дiйсну величину трикутника.
Якщо ж задана площина i проекцiюючою (рис. 7), то розглядувана задача розвтАЩязуiться однiiю замiною площин. В цьому випадку площина р4, паралельна трикутнику ABC, утворюi з р2 ортогональну систему р2/ р4. Нова проекцiя А4В4С4 на площину р4 визначаi дiйсну величину трикутника.
