Устойчивость по Ляпунову
Устойчивость решений дифференциальных систем и функции Ляпунова
Устойчивость по Ляпунову
Метод функций Ляпунова. Теоремы Ляпунова
Методы построения функций Ляпунова
Понятие продолжимости решения. Признак Винтера-Еругина
Применение функций Ляпунова к исследованию продолжимости решений дифференциальных систем
Развитие метода функций Ляпунова
Функции Ляпунова и продолжимость решений дифференциальных уравнений
Продолжимость всех решений некоторых уравнений третьего порядка
Заключение
Список использованных источников
Введение
Понятие функций Ляпунова появилось в связи с развитием теории устойчивости, начало которой положили труды великого русского математика А.М. Ляпунова. Рождение теории устойчивости как самостоятельной научной дисциплины можно отнести ко времени появления докторской диссертации А.М. Ляпунова "Общая задача об устойчивости движения", впервые опубликованной в Харькове в 1892 году. За последние годы наблюдается бурный рост этой теории, вызванный потребностями развивающейся техники, в частности, теории автоматического регулирования и управления.
Развитие теории устойчивости движения осуществляется двумя путями: во-первых, расширением круга задач и, во-вторых, созданием новых и усилением уже известных методов исследования. Метод функций Ляпунова (известный также как второй или прямой метод Ляпунова) является одним из наиболее эффективных методов исследования устойчивости, чем вызвано и его широкое применение в теории управления. Значение его далеко не исчерпывается возможностью установления факта устойчивости или неустойчивости исследуемой системы. Удачно построенная функция Ляпунова для конкретной системы позволяет решать целый комплекс задач, которые имеют важное прикладное значение, например, получение оценки изменения регулируемой величины, оценки времени регулирования, оценки качества регулирования, оценки области притяжения (множества всех начальных возмущений, исчезающих во времени), оценки влияния постоянно действующих возмущений и другие.
Функции Ляпунова позволяют решать вопросы устойчивости в "большом", т.е. оценивать область начальных возмущений, не выходящих с течением времени за пределы заданной области. С помощью функций Ляпунова решается проблема существования или отсутствия периодических решений, устанавливается ограниченность и продолжимость всех решений заданной нелинейной системы обыкновенных дифференциальных уравнений.
В связи с широким применением функций Ляпунова возник вопрос универсальности этого метода. Решением этой задачи занимались Я.П. Персидский, Н.Н. Красовский, Е.А. Барбашин, Я. Курцвейль, Ж.Л. Массера и другие математики. Было установлено, что в теории устойчивости этот метод универсален для широкого круга задач. В этой связи возникла задача о методах построения функций Ляпунова. Следует заметить, что известные методы построения функций Ляпунова, разработанные для получения достаточных условий устойчивости, не являются достаточно эффективными, поскольку каждый из них приспособлен для исследования конкретных систем. Поэтому проблему построения функций Ляпунова для нелинейных систем в настоящее время нельзя считать решенной.
Данная работа содержит исследования вопроса о применении функций Ляпунова к исследованию продолжимости решений дифференциальных уравнений.
Устойчивость решений дифференциальных систем и функции Ляпунова
В данной работе мы будем рассматривать системы дифференциальных уравнений в нормальной форме. Напомним, что система обыкновенных
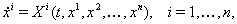 (??)
(??)
дифференциальных уравнений называется Ванормальной. В этой системе 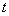 Ва--- независимая переменная,
Ва--- независимая переменная, 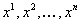 Ва--- неизвестные функции этой переменной, а
Ва--- неизвестные функции этой переменной, а 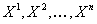 Ва--- функции от
Ва--- функции от 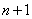 Вапеременной, заданные на множестве
Вапеременной, заданные на множестве  Вапространства размерности
Вапространства размерности 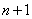 , в котором координатами точки являются числа
, в котором координатами точки являются числа 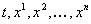 . В дальнейшем будем предполагать, что функции
. В дальнейшем будем предполагать, что функции
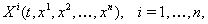 (??)
(??)
непрерывны на открытом множестве  ; также будем предполагать, что их частные производные
; также будем предполагать, что их частные производные
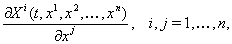 (??)
(??)
существуют и непрерывны на множестве  . Следует заметить, что частные производные (??), непрерывность которых предполагается, берутся только по переменным
. Следует заметить, что частные производные (??), непрерывность которых предполагается, берутся только по переменным 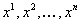 , а не по независимой переменной
, а не по независимой переменной 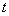 .
.
Решением системы уравнений (??) называется система непрерывных функций
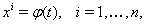 (??)
(??)
определенных на некотором интервале 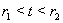 Ваи удовлетворяющих системе (??). Интервал
Ваи удовлетворяющих системе (??). Интервал 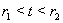 Ваназывается Ваинтервалом определения решения (??) (случаи
Ваназывается Ваинтервалом определения решения (??) (случаи 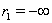 ,
, 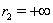 Ване исключаются). Считается, что система функций (??) удовлетворяет системе уравнений (??), если при подстановке в соотношение (??) вместо
Ване исключаются). Считается, что система функций (??) удовлетворяет системе уравнений (??), если при подстановке в соотношение (??) вместо 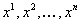 Вафункций (??) соотношения (??) превращаются в тождества по
Вафункций (??) соотношения (??) превращаются в тождества по 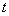 Вана всем интервале
Вана всем интервале 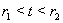 Ваи чтобы правые части уравнений (??) были определены для всех подставляемых в них значений аргументов. Таким образом, точка с координатами
Ваи чтобы правые части уравнений (??) были определены для всех подставляемых в них значений аргументов. Таким образом, точка с координатами 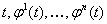 Вадолжна принадлежать множеству
Вадолжна принадлежать множеству  Вадля всех значений
Вадля всех значений 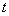 Вана интервале
Вана интервале 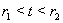 .
.
Рассмотрим систему дифференциальных уравнений
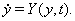 (??)
(??)
Выделим некоторое решение 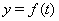 Васистемы (??) и назовем его невозмущенным решением.
Васистемы (??) и назовем его невозмущенным решением.
Решение 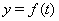 Ваназовем Ваустойчивым в смысле Ляпунова, если для любого
Ваназовем Ваустойчивым в смысле Ляпунова, если для любого 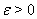 Ваможно указать
Ваможно указать 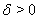 Ватакое, что из неравенства
Ватакое, что из неравенства 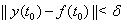 Васледует неравенство
Васледует неравенство 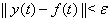 Вапри
Вапри 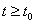 . Здесь через
. Здесь через 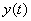 Ваобозначено любое другое решение системы (??), определяемое начальным условием
Ваобозначено любое другое решение системы (??), определяемое начальным условием 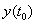 . Решение
. Решение 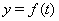 Ваназывается Ваасимптотически устойчивым в смысле Ляпунова, если оно устойчиво в смысле Ляпунова и если существует такое
Ваназывается Ваасимптотически устойчивым в смысле Ляпунова, если оно устойчиво в смысле Ляпунова и если существует такое 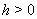 , что при
, что при 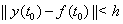 Вабудем иметь
Вабудем иметь
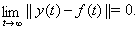 (??)
(??)
Пример ВаРешение 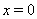 Вауравнения
Вауравнения 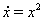 Ване является устойчивым ни справа, ни слева, т.к. каждое решение
Ване является устойчивым ни справа, ни слева, т.к. каждое решение 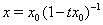 , где
, где 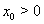 Ва(
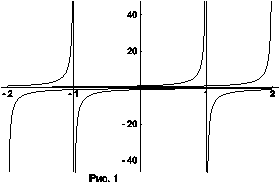
Ва(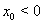 ), перестает существовать при
), перестает существовать при 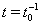 Ва(рис. 1).
Ва(рис. 1).
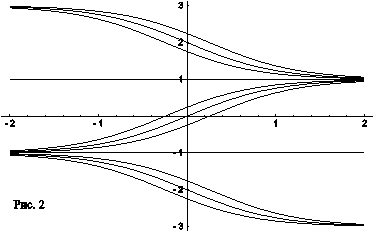
Пример. Решение 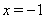 Вауравнения
Вауравнения 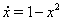 Ванеустойчиво справа, т.к. все решения
Ванеустойчиво справа, т.к. все решения 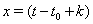 ,
, 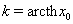 ,
, 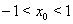 , приближаются к
, приближаются к 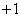 Вапри
Вапри 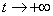 . Каждое решение
. Каждое решение 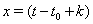 Ватак же, как и решение
Ватак же, как и решение 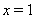 , является асимптотически устойчивым справа (рис. 2).
, является асимптотически устойчивым справа (рис. 2).
Проведем в системе (??) замену переменных 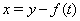 . Новая система будет иметь вид
. Новая система будет иметь вид
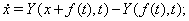
вводя обозначение
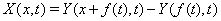
получим систему
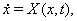 (??)
(??)
где 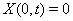 Вапри
Вапри 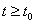 . Решение
. Решение 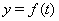 Ваперешло при рассматриваемой замене переменных в положение равновесия
Ваперешло при рассматриваемой замене переменных в положение равновесия 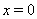 Вановой системы. Задача устойчивости решения
Вановой системы. Задача устойчивости решения 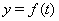 Вапереходит, таким образом, в задачу устойчивости нулевого (тривиального) решения
Вапереходит, таким образом, в задачу устойчивости нулевого (тривиального) решения 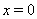 Васистемы (??).
Васистемы (??).
Приведем определение устойчивости нулевого решения системы (??).
Решение 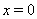 Васистемы (??) называется Ваустойчивым в смысле Ляпунова, если для любого
Васистемы (??) называется Ваустойчивым в смысле Ляпунова, если для любого 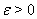 Ваможно указать
Ваможно указать 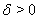 Ватакое, что из неравенства
Ватакое, что из неравенства 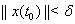 Васледует неравенство
Васледует неравенство 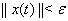 Вапри
Вапри 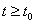 . Если же, кроме того, всякое решение
. Если же, кроме того, всякое решение 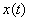 , начальные данные которого определяются условием
, начальные данные которого определяются условием 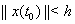 , обладает свойством
, обладает свойством 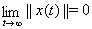 , то нулевое решение называется Ваасимптотически устойчивым в смысле Ляпунова.
, то нулевое решение называется Ваасимптотически устойчивым в смысле Ляпунова.
Проиллюстрируем идею метода на простейшем примере:
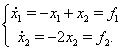 (??)
(??)
Рассмотрим функцию 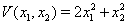 . Эта функция положительна всюду, кроме точки
. Эта функция положительна всюду, кроме точки 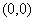 , где она обращается в нуль. В пространстве переменных
, где она обращается в нуль. В пространстве переменных 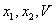 Вауравнение
Вауравнение 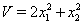 Ваопределяет параболоид с вершиной в начале координат. Линии уровня этой поверхности на плоскости
Ваопределяет параболоид с вершиной в начале координат. Линии уровня этой поверхности на плоскости 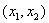 Вапредставляют собой эллипсы. Зададим произвольно малое
Вапредставляют собой эллипсы. Зададим произвольно малое 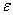 . Построим на плоскости
. Построим на плоскости 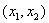 Вакруг
Вакруг 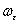 Варадиуса
Варадиуса 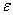 . Возьмем одну из линий уровня --- эллипс, целиком лежащий внутри круга
. Возьмем одну из линий уровня --- эллипс, целиком лежащий внутри круга 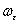 . Построим другой круг
. Построим другой круг 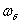 Вацеликом лежащий внутри эллипса (рис. 3).
Вацеликом лежащий внутри эллипса (рис. 3).
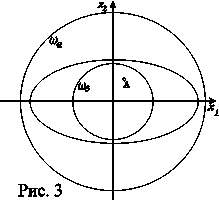
Пусть начальная точка 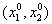 Валежит внутри
Валежит внутри 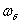 .
.
Рассмотрим функцию двух переменных 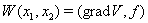 . Легко видеть, что если вместо
. Легко видеть, что если вместо 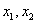 Ваподставить решение системы (??), то полученная таким образом, функция от
Ваподставить решение системы (??), то полученная таким образом, функция от 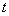 Вабудет представлять собой полную производную функции
Вабудет представлять собой полную производную функции 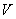 Вавдоль траектории решения системы (??). Если эта производная вдоль любой траектории, начинающейся в
Вавдоль траектории решения системы (??). Если эта производная вдоль любой траектории, начинающейся в 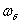 , неположительна, то это будет означать, что траектория не сможет покинуть
, неположительна, то это будет означать, что траектория не сможет покинуть 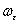 , так как иначе между
, так как иначе между 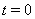 Ваи значением
Ваи значением 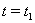 , при котором она попадет на границу
, при котором она попадет на границу 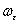 , найдется значение
, найдется значение 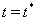 , для которого
, для которого 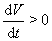 , поскольку
, поскольку 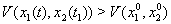 . То, что ни одна траектория, начинающаяся в
. То, что ни одна траектория, начинающаяся в 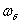 , не покидает ни при одном
, не покидает ни при одном 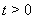 Вакруг
Вакруг 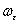 , означает устойчивость тривиального решения.
, означает устойчивость тривиального решения.
Итак, мы должны проверить знак 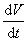 Вавдоль траектории. Для этого надо знать саму траекторию. Хотя в данном примере это можно сделать, но метод должен быть рассчитан на систему общего вида, для которого
Вавдоль траектории. Для этого надо знать саму траекторию. Хотя в данном примере это можно сделать, но метод должен быть рассчитан на систему общего вида, для которого 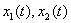 Ванельзя выписать явно и тем самым нельзя проверить нужное неравенство. Поэтому мы будем требовать, чтобы функция
Ванельзя выписать явно и тем самым нельзя проверить нужное неравенство. Поэтому мы будем требовать, чтобы функция 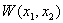 Вабыла неположительной как функция двух независимых переменных
Вабыла неположительной как функция двух независимых переменных 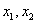 Вапо крайней мере в некоторой окрестности
Вапо крайней мере в некоторой окрестности 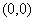 . Это условие можно проверить непосредственно по правым частям системы не зная решения. В нашем примере именно так и будет, поскольку
. Это условие можно проверить непосредственно по правым частям системы не зная решения. В нашем примере именно так и будет, поскольку 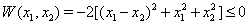 Вавсюду на плоскости
Вавсюду на плоскости 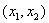 , а тем самым вдоль любой траектории, и устойчивость тривиального решения гарантирована. Функция
, а тем самым вдоль любой траектории, и устойчивость тривиального решения гарантирована. Функция 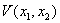 Ваи есть функция Ляпунова для рассмотренного примера. Она имеет вид квадратичной формы, хотя в принципе можно было взять любую другую функцию, лишь бы она была положительной всюду, кроме точки
Ваи есть функция Ляпунова для рассмотренного примера. Она имеет вид квадратичной формы, хотя в принципе можно было взять любую другую функцию, лишь бы она была положительной всюду, кроме точки 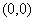 , где она обращается в нуль, а выражение
, где она обращается в нуль, а выражение 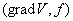 Вабыло неположительное. Обратимся теперь к формулировке некоторых общих теорем, в основу которых положена эта идея. Будем исследовать тривиальное решение системы (??).
Вабыло неположительное. Обратимся теперь к формулировке некоторых общих теорем, в основу которых положена эта идея. Будем исследовать тривиальное решение системы (??).
Все дальнейшие построения будем вести в некоторой 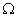 -окрестности начала координат в фазовом пространстве. Пусть для определенности
-окрестности начала координат в фазовом пространстве. Пусть для определенности 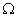 Вазадается неравенством
Вазадается неравенством 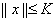 ,
, 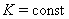 . Функция
. Функция 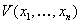 Ва(или короче
Ва(или короче 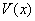 ) называется Ваположительно определенной в
) называется Ваположительно определенной в 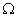 , если
, если 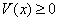 Вав
Вав 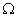 , причем
, причем 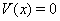 Ватогда и только тогда, когда
Ватогда и только тогда, когда 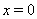 .
.
Приведем ряд утверждений, показывающих применение функций Ляпунова [??].
Теорема Первая теорема Ляпунова
Пусть в 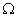 Васуществует непрерывная вместе с частными производными первого порядка положительно определенная функция
Васуществует непрерывная вместе с частными производными первого порядка положительно определенная функция 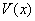 Ватакая, что функция
Ватакая, что функция 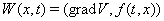 Ваудовлетворяет неравенству
Ваудовлетворяет неравенству
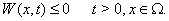 (??)
(??)
Тогда тривиальное решение системы (??) устойчиво.
Теорема Вторая теорема Ляпунова
Пусть дополнительно к условиям первой теоремы для 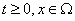 Вавыполняется неравенство
Вавыполняется неравенство 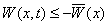 , где
, где 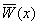 Ва--- положительно определенная в
Ва--- положительно определенная в 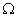 Вафункция.
Вафункция.
Тогда тривиальное решение системы (??) асимптотически устойчиво.Ва
Теорема Третья теорема Ляпунова
Пусть в 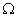 Васуществует непрерывная вместе с частными производными первого порядка положительно определенная функция
Васуществует непрерывная вместе с частными производными первого порядка положительно определенная функция 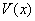 Ватакая, что
Ватакая, что
а) 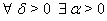 Ваи
Ваи 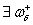
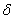 -окрестность точки
-окрестность точки 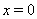 , в которой выполняется неравенство
, в которой выполняется неравенство 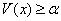 ;
;
б) 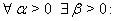 Ваиз
Ваиз 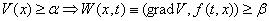 , справедливое при всех
, справедливое при всех 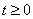 .
.
Тогда тривиальное решение системы неустойчиво.
Замечание. Недостаток изложенных методов заключается в том, что не существует достаточно общего конструктивного способа построения функций 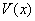 .
.
Замечание. Горбунов [??] показал, что для линейных систем с непрерывными коэффициентами функция Ляпунова всегда существует в виде квадратичной формы.
Замечание. Для дифференциальных уравнений, описывающих некоторые механические системы, роль функции Ляпунова играет потенциальная энергия 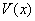 . Сама система имеет вид
. Сама система имеет вид 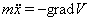 , а соответствующая функция
, а соответствующая функция 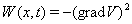 .
.
В замечании (??) было обращено внимание на отсутствие общей методики построения функций Ляпунова для конкретных дифференциальных систем. Ниже приведены некоторые известные способы построения функций Ляпунова.
Методы построения функций ЛяпуноваПрименяется для системы второго порядка.
Рассмотрим систему
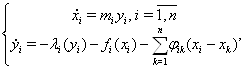 (??)
(??)
где 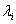 ,
, 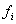 ,
, 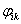 Ванепрерывны,
Ванепрерывны, 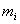 Ва--- положительные постоянные и
Ва--- положительные постоянные и 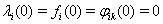 ,
, 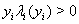 Вапри
Вапри 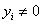 ,
, 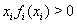 Вапри
Вапри 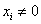 ,
, 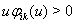 Вапри
Вапри 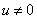 , где
, где 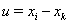 ,
, 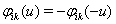 ,
, 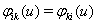 .
.
В качестве механической модели можно взять движение системы 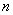 Ваматериальных точек
Ваматериальных точек 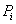 Вас массой
Вас массой 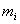 , в которой точка
, в которой точка 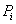 Ваподвергается действию сил
Ваподвергается действию сил 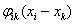 , выражающие влияние других точек
, выражающие влияние других точек 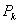 Ваэтой системы на точку
Ваэтой системы на точку 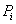 .
.
Тогда можно дать механическую интерпретацию. Функцию 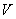 Васоставим как полную энергию системы, то есть как сумму кинетической и потенциальной энергий. Получим
Васоставим как полную энергию системы, то есть как сумму кинетической и потенциальной энергий. Получим
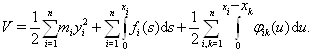
Очевидно, что эта функция определенно положительная.
Найдем производную функции 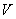 Вав силу системы (??), получим
Вав силу системы (??), получим
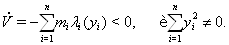 (??)
(??)
Так как члены 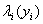 Ваопределяют силы, способствующие рассеиванию механической энергии, то полная энергия системы убывает, а значит, соображений производная (??) знакоотрицательная.
Ваопределяют силы, способствующие рассеиванию механической энергии, то полная энергия системы убывает, а значит, соображений производная (??) знакоотрицательная.
Рассмотрим уравнение
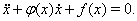 (??)
(??)
Это уравнение эквивалентно системе
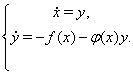 (??)
(??)
Соответствующая линейная система имеет вид
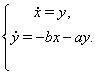 (??)
(??)
Для нее может быть построена функция Ляпунова
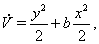
причем 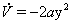 .
.
Замечаем теперь, что 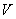 Ване содержит в своей записи параметра
Ване содержит в своей записи параметра 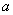 , поэтому эта же функция пригодна для исследования системы
, поэтому эта же функция пригодна для исследования системы

но непригодна для системы (??).
Чтобы получить функцию Ляпунова для системы (??), необходимо найти аналог члена 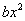 Вав записи
Вав записи 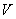 . Но с точки зрения механики величина
. Но с точки зрения механики величина 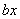 Ва(или
Ва(или 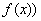 Вахарактеризует восстанавливающую силу, а величина
Вахарактеризует восстанавливающую силу, а величина 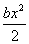 Васоответствует потенциальной энергии. Поэтому естественно принять за функцию Ляпунова для системы (??) функцию
Васоответствует потенциальной энергии. Поэтому естественно принять за функцию Ляпунова для системы (??) функцию
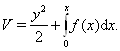 (??)
(??)
Очевидно, получим в силу системы (??)
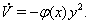
Условия устойчивости в целом запишутся следующим образом:
а) 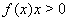 Вапри
Вапри  ,
,
б) 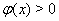 ,
,
в) 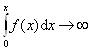 Вапри
Вапри 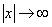 .
.
Легко проверить, что множество 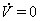 , то есть прямая
, то есть прямая 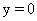 Ване содержит целых траекторий, кроме начала координат.
Ване содержит целых траекторий, кроме начала координат.
Укажем другой подход к задаче. Производя в уравнении (??) замену переменной 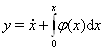 Ваполучим систему
Ваполучим систему
 (??)
(??)
Используя снова прежнюю функцию Ляпунова (??), получим в силу системы (??)
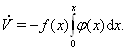
Условия устойчивости в целом в данном случае улучшаются, так как условие б) заменяется менее ограничительным условием
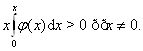
Рассмотрим систему
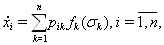 (??)
(??)
где 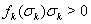 Вапри
Вапри  Ва--- постоянные,
Ва--- постоянные, 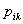 Вамогут быть функциями координат, параметров и времени.
Вамогут быть функциями координат, параметров и времени.
Определенно положительная функция
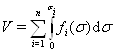
имеет производную в силу системы (??) в следующем виде:
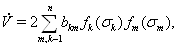
где
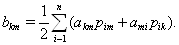
Таким образом, 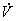 Вабудет определенно отрицательной или знакоотрицательной, если этим же свойством обладает форма
Вабудет определенно отрицательной или знакоотрицательной, если этим же свойством обладает форма
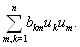
Как известно, критерий Сильвестра легко переносится на случай квадратичных форм с переменными коэффициентами, и поэтому этот критерий с успехом может быть использован.
В качестве примера построим функцию Ляпунова для системы уравнений переходного процесса синхронного двигателя
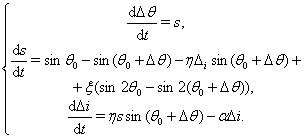 (??)
(??)
Здесь 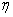 ,
, 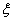 Ва--- постоянные,
Ва--- постоянные, 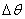 Ва--- возмущение рабочего угла,
Ва--- возмущение рабочего угла, 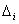 Ва--- возмущение силы тока, возникающее в результате наброса нагрузки на двигатель.
Ва--- возмущение силы тока, возникающее в результате наброса нагрузки на двигатель.
В данном случае получаем
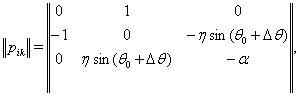
а в качестве матрицы 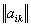 Ваберем единичную матрицу. Таким образом, получим
Ваберем единичную матрицу. Таким образом, получим
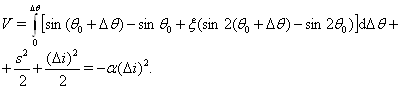
Построенная функция Ляпунова позволяет оценить область притяжения положения равновесия, что дает возможность быстро оценить допустимую предельную нагрузку на синхронный двигатель.
Предложенный метод в линейном случае дает необходимые и достаточные условия устойчивости, если найти подходящие выражения для 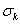 . Это следует из того, что всякая определенно положительная квадратичная форма линейным преобразованием может быть приведена к каноническому виду, т. е. к сумме квадратов переменных. Трудность этого метода состоит в подборе
. Это следует из того, что всякая определенно положительная квадратичная форма линейным преобразованием может быть приведена к каноническому виду, т. е. к сумме квадратов переменных. Трудность этого метода состоит в подборе 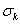 Ваи матрицы
Ваи матрицы 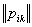 .
.
Исследуется система уравнений
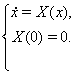 (??)
(??)
Функция Ляпунова строится в виде 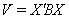 , где симметричная матрица
, где симметричная матрица 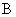 Ваподбирается так, чтобы ее собственные числа были положительны и чтобы симметризованная матрица
Ваподбирается так, чтобы ее собственные числа были положительны и чтобы симметризованная матрица
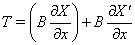 (??)
(??)
удовлетворяла критерию отрицательности Сильвестра. Имеем в силу системы (??)

Таким образом, получим 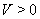 Ваи
Ваи 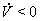 .
.
В качестве примера рассмотрим уравнение
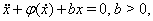
эквивалентное системе
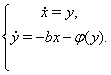
Функцию Ляпунова выбираем в виде
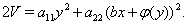
Легко видеть, что
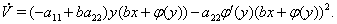
Очевидно, следует принять 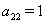 Ваи
Ваи 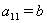 , тогда будем иметь
, тогда будем иметь
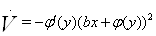
и условие устойчивости в целом принимает вид 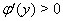 Вапри любых
Вапри любых 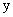 .
.
Рассмотрим уравнение
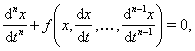 (??)
(??)
эквивалентное системе
 (??)
(??)
Функцию Ляпунова для системы (??) предлагается брать в виде
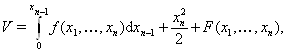 (??)
(??)
где 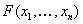 Васпециально подбирается с целью упрощения вида
Васпециально подбирается с целью упрощения вида 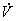 Ваи с целью выполнения неравенства
Ваи с целью выполнения неравенства 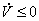 .
.
Так, например, для системы
 (??)
(??)
функцию 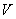 Вабудем искать в виде
Вабудем искать в виде
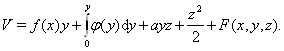
Имеем в силу системы (??)
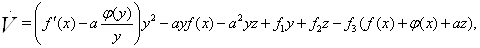
где
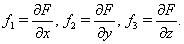
Очевидно, проще всего положить 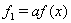 ,
, 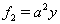 ,
, 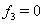 , откуда
, откуда
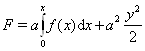
и получаем функцию
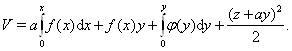 (??)
(??)
В качестве второго примера рассмотрим уравнение
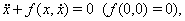 (??)
(??)
эквивалентное системе
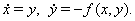 (??)
(??)
Согласно предложенному способу следует принять
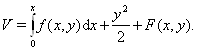
Имеем тогда
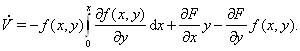
Если положить 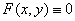 , то условия устойчивости будут иметь вид
, то условия устойчивости будут иметь вид
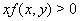 Ваи
Ваи 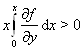 .
.
Но эти условия не могут быть удовлетворены для линейной функции
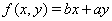 .
.
Значительно полезней оказывается функция, предложенная Л. Америо ,
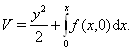
В данном случае получим
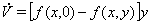
и условия устойчивости в целом принимают вид
а) 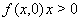 Вапри
Вапри  ,
,
б) 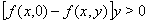 Вапри
Вапри 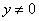 ,
,
в)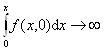 при
при 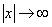 .
.
Предлагается начинать поиск функций Ляпунова с записи градиента этой функции в форме
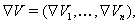
где
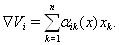
Функции 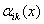 Ваподбираются из условия отрицательности
Ваподбираются из условия отрицательности 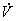 Ваи из требования, чтобы векторное поле
Ваи из требования, чтобы векторное поле 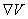 Вабыло потенциальным. Это значит, что должны выполняться условия
Вабыло потенциальным. Это значит, что должны выполняться условия 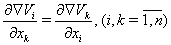 . После того как найден градиент
. После того как найден градиент 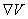 Васама функция
Васама функция 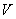 Ваопределяется как криволинейный интеграл
Ваопределяется как криволинейный интеграл
 (??)
(??)
В качестве примера рассмотрим уравнение
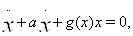 (??)
(??)
где 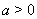 . Это уравнение эквивалентно системе
. Это уравнение эквивалентно системе
 (??)
(??)
Будем искать вектор-градиент 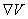 Вав форме
Вав форме
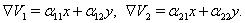
В силу системы (??) получим
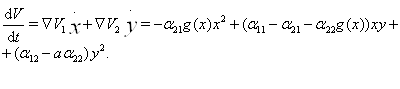
Удобно положить 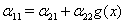 ,
, 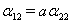 ,
, 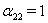 . Условия потенциальности поля дают
. Условия потенциальности поля дают 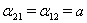 . Таким образом, имеем
. Таким образом, имеем 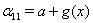 ,
, 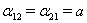 ,
, 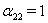 . Формула (??) дает нам
. Формула (??) дает нам
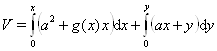
или, что то же самое,

Так как 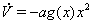 , то условия устойчивости имеют вид
, то условия устойчивости имеют вид 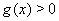 Ваи
Ваи
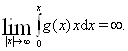
Понятие продолжимости решения. Признак Винтера-ЕругинаПусть
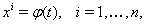 (??)
(??)
--- решение системы уравнений (??), определенное на некотором интервале 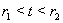 , и
, и
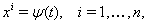 (??)
(??)
Ва--- решение той же системы уравнений (??), определенное на некотором интервале 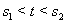 . Будем говорить, что решение
. Будем говорить, что решение  Ваявляется Вапродолжением решения (??), если
Ваявляется Вапродолжением решения (??), если 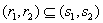 . Решение (??) будем называть Ванепродолжаемым, если не существует никакого отличного от него решения, являющегося его продолжением.
. Решение (??) будем называть Ванепродолжаемым, если не существует никакого отличного от него решения, являющегося его продолжением.
Покажем, что каждое решение может быть продолжено до решения, далее непродолжаемого. В этом смысле непродолжаемые решения исчерпывают совокупность всех решений.
Пусть
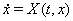 (??)
(??)
Ва--- векторная запись нормальной системы уравнений (??). Тогда справедлива следующая теорема [??]:Ва
Теорема 1. Существует непродалжаемое решение уравнения (??) с произвольными начальными значениями из  .
.
2. Если некоторое непродолжаемое решение уравнения (??) совпадает с некоторым другим решением уравнения (??), хотя бы при одном значении 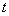 , то оно является продолжением этого решения.
, то оно является продолжением этого решения.
3. Если два непродолжаемых решения уравнения (??) совпадают между собой хотя бы для одного значения 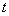 , то они полностью совпадают, т.е. имеют один и тот же интервал определения и равны на нем.
, то они полностью совпадают, т.е. имеют один и тот же интервал определения и равны на нем.
Пусть 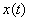 Ва--- решение системы (??) с начальным условием
Ва--- решение системы (??) с начальным условием 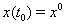 . Ясно, что:
. Ясно, что:
а) либо это решение может быть продолжено для всех значений 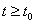 , и тогда будем говорить, что решение
, и тогда будем говорить, что решение 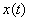 ВаВанеограниченно (бесконечно) продолжаемо [в право];
ВаВанеограниченно (бесконечно) продолжаемо [в право];
б) либо существует такое 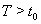 , что
, что 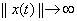 Вапри
Вапри 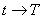 , и тогда будем говорить, что решение
, и тогда будем говорить, что решение 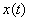 Ваимеет Ваконечное время определения.
Ваимеет Ваконечное время определения.
Эти две возможности явно несовместимы и дополняют друг друга. Третий случай
в) решение ограничено.
--- совместим с возможностью а), но, конечно, несовместим с б).
Отметим, следующееВа
ВаВаСвойство ВаВаЕсли решение 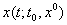 Ваограничено в своем максимальном промежутке существования
Ваограничено в своем максимальном промежутке существования 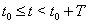 , то оно бесконечно продолжаемо, т.е.
, то оно бесконечно продолжаемо, т.е. 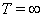 .
.
Ограниченность Вавсех решений представляет собой своего рода устойчивость; в этом случае говорят об Ваустойчивости в смысле Лагранжа или, короче, об Ваустойчивости по Лагранжу.
Неограниченная продолжимость решений системы (??) является Ванеобходимым условием устойчивости по Ляпунову решений этой системы.
Пример
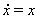
Все решения данного уравнения 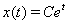 Вабесконечно продолжаемы, но не ограничены.
Вабесконечно продолжаемы, но не ограничены.
Пример
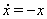
На интервале 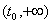 , для любого
, для любого 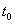 Вавсе решения данного уравнения
Вавсе решения данного уравнения 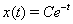 Вабесконечно продолжаемы и ограничены.
Вабесконечно продолжаемы и ограничены.
Пример
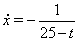
Все решения 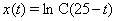 ,
, 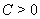 Ваимеют конечное время определения.
Ваимеют конечное время определения.
Приведем без доказательства теорему Майергофера-Еругина.
Теорема Майергофера-Еругина
Пусть решение 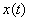 Вауравнения
Вауравнения
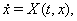 (??)
(??)
где функция 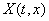 Ванепрерывна для всех
Ванепрерывна для всех 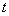 Ваи
Ваи 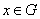 , определено на промежутке
, определено на промежутке 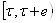 Ваи непродолжимо для значений
Ваи непродолжимо для значений 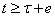 .
.
Тогда при 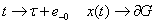 , где
, где 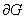 Ва--- граница области
Ва--- граница области 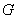 .
.
Предположим теперь, что в окрестности любой точки  Вавыполняются условия существования решения уравнения (??). Для простоты предположим, что
Вавыполняются условия существования решения уравнения (??). Для простоты предположим, что 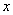 Ва--- скаляр.
Ва--- скаляр.
Теорема признак Винтнера-Еругина
Пусть функция 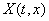 Вауравнения (??) определена и непрерывна для всех вещественных
Вауравнения (??) определена и непрерывна для всех вещественных 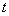 Ваи
Ваи 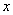 Вакак функция двух переменных.
Вакак функция двух переменных.
Тогда любое решение уравнения (??) неограниченно продолжим в обе стороны, если только выполнено неравенство
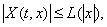
где 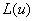 --- функция, удовлетворяющая условию
--- функция, удовлетворяющая условию
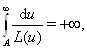 (??)
(??)
где 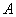 --- число.Ва
--- число.Ва
Доказательство проведем методом от противного.
Пусть существует решение 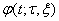 , которое не является неограниченно продолжимым, например, вправо. Тогда на основании теоремы Майергофера-Еругина существует некоторое число
, которое не является неограниченно продолжимым, например, вправо. Тогда на основании теоремы Майергофера-Еругина существует некоторое число 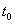 Ватакое, что
Ватакое, что 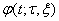 Вапринимает
Вапринимает 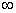 Варазных знаков и при
Варазных знаков и при 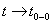 .
.
Ввиду непрерывности решения 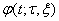 Вакак функции от
Вакак функции от 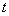 Ваоно должно бесконечное число раз проходить через нуль. А это означает, что существует последовательность значений
Ваоно должно бесконечное число раз проходить через нуль. А это означает, что существует последовательность значений 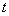 , по которой это решение стремится к нулю. Это невозможно (по теореме Майергофера-Еругина).
, по которой это решение стремится к нулю. Это невозможно (по теореме Майергофера-Еругина).
Допустим, что 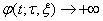 Вапри
Вапри 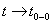 . Так как
. Так как 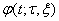 Ва--- решение уравнения (??), то
Ва--- решение уравнения (??), то 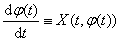 Вав промежутке
Вав промежутке 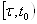 . Допустим, что
. Допустим, что 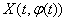 Ване меняет знак. Тогда
Ване меняет знак. Тогда
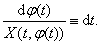 (??)
(??)
Проинтегрируем обе части (??) по отрезку 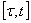 , где
, где 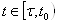 Ваполучим
Ваполучим
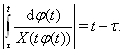
Произведем замену 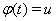 . Получим
. Получим
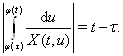
Тогда
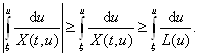
Таким образом получаем
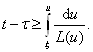
Теперь пусть 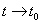 . Учтем, что с заменой
. Учтем, что с заменой 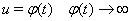 Ваи получаем
Ваи получаем
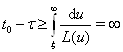
по условию теоремы. Это неравенство противоречиво, так как слева стоит конечная величина.
Рассмотрим общий случай, когда 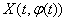 Ваможет менять знак. Тогда
Ваможет менять знак. Тогда
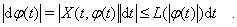
Так как 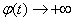 Вапри
Вапри 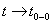 , то с некоторого момента величина
, то с некоторого момента величина 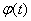 Вастанет положительной и знак модуля можно будет опустить. Тогда получим
Вастанет положительной и знак модуля можно будет опустить. Тогда получим
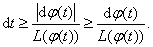
Проинтегрируем обе части от 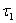 Вадо
Вадо 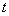 , где
, где 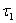 Ва--- значение, после которого
Ва--- значение, после которого 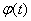 Вастановится положительным.
Вастановится положительным.
Сделаем замену 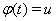 , получим
, получим

Устремим 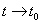 Ваи учтем (??)
Ваи учтем (??)
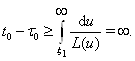
Последнее неравенство противоречиво, что говорит о том, что не существует решения, которое не является неограниченно продолжимым вправо.
Применение функций Ляпунова к исследованию продолжимости решений дифференциальных системМетод функций Ляпунова дал довольно сильный и гибкий аппарат исследования устойчивости решений дифференциальных уравнений. Модификации этого используют сейчас и для выявления других свойств решений дифференциальных уравнений. Например, японский математик Окамура использовал идеи, сходные с идеями второго метода Ляпунова, для изучения продолжимости решений, а затем Йошизава применил этот метод для получения сведений об ограниченности решений.
Как известно, Теоремы Ляпунова дают возможность судить об устойчивости по знаку производной 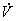 , где
, где 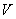 Ва--- положительно определенная функция. Таким образом изучается неравенство
Ва--- положительно определенная функция. Таким образом изучается неравенство 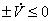 . После работ русского ученог
. После работ русского ученог
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Аксонометричнi проекцii