Факторiальнi кiльця та iх застосування

Курсова робота

на тему:

ВлФакторiальнi кiльця та iх застосуванняВ»

Вступ

Завдання алгебри i вивчення алгебраiчних структур. Безперечно, алгебра вивчаi далеко не всi алгебраiчнi структури. Можна побудувати чимало прикладiв алгебраiчних структур, але в переважнiй бiльшостi вони не матимуть нiяких застосувань нi в теорii, нi в практицi, а ВлтеорiяВ» таких структур складатиметься з означень i тривiальних наслiдкiв з них. Такi структури, очевидно, не можуть бути об'iктом вивчення.

У процесi розвитку математики видiлилася й стала докладно вивчатися невелика кiлькiсть основних типiв алгебраiчних структур, алгебраiчнi операцii в яких за своiми властивостями бiльш-менш близькi до операцiй додавання i множення чисел. Найважливiшими серед рiзних алгебраiчних структур i група, кiльце, поле, лiнiйний простiр, лiнiйна алгебра. Вивчення властивостей саме цих алгебраiчних структур, опис iх будови i зв'язкiв мiж ними й iншими основними математичними об'iктами i одним з найважливiших завдань алгебри на сучасному етапi ii розвитку.

У цiй роботi буде детально розглянуто властивостi та особливостi таких алгебраiчних структур, як кiльця. А саме, розглядатимуться кiльця, якi i факторiальними, тобто кiльця, що i областю цiлiсностi i будь-який iхнiй елемент, вiдмiнний вiд нуля i дiльникiв одиницi, однозначно (з точнiстю до дiльникiв одиницi i порядку множникiв) розкладаiться на добуток простих множникiв. Зокрема будуть дослiджуватись кiльця головних iдеалiв, евклiдовi кiльця, кiльця многочленiв вiд однiii та вiд кiлькох змiнних.

Кожний роздiл теоретичного матерiалу супроводжуiться задачами, в розвтАЩязаннi яких пiдтверджуються на практицi теореми та властивостi, якi були доведенi в теоретичнiй частинi, та розглядаються окремi конкретнi випадки, якi допомагають краще зрозумiти той чи iнший нюанс тiii чи iншоi теми зокрема та теорii кiлець в цiлому.

1. Кiльця: означення та приклади

Означення Непорожня множина K на якiй визначено двi бiнарнi алгебраiчнi операцii Вл+В» i ВлВ·В» називаiться кiльцем, якщо виконуються умови:

1. "a, b [a+b=b+a];

2. "a, b, c [(a+b)+c=a+(b+c)];

3. $θ,"a [a+θ=a];

4. "a $ã [a+ã=θ];

5. "a, b, c [(ab) c=a(bc)];

6. "a, b, c [(a+b) c=ac+bc];

7. "a, b, c [c (a+c)=ca+cb];

Якщо операцiя множення комутативна, то кiльце комутативне. Першi чотири аксiоми означають, що вiдносно операцii додавання кiльце утворюi адитивну абелеву групу.

Приклади кiлець, що наводяться нижче свiдчать про те, що система аксiом кiльця несуперечлива.

№1 Множина цiлих чисел Z i комутативне кiльце вiдносно визначених у нiй операцiй додавання i множення. Справдi, множина Z i абелева група по додаванню, операцiя множення чисел, як вiдомо, асоцiативна, комутативна i дистрибутивна вiдносно операцii додавання.

№2 Множина парних чисел i комутативне кiльце вiдносно операцiй додавання i множення чисел. Справдi, ця множина i абельова група по додаванню, в нiй визначена операцiя множення: добуток парних чисел i парне число, причому операцiя множення асоцiативна, комутативна i дистрибутивна вiдносно операцii додавання.

№3 Множина R всiх дiйсних чисел, очевидно також i кiльце вiдносно визначених у нiй операцiй додавання i множення.

№4 Множина K всiх чисел виду , де a i b тАУ будь-якi рацiональнi числа, i комутативне кiльце вiдносно визначених у нiй операцiй додавання i множення. Справдi, якi б ми не взяли числа a₁+b₁Ваi a₂+b₂Ваз множини K, iх сума (a₁+b₁)+(a₂+b₂)=(a₁+a₂)+(b₁+b₂), добуток (a₁+b₁) (a₂+b₂)= =(a₁a₂+2b₁b₂)+(a₁b₂+b₁a₂)Ваi рiзниця (a₁+b₁) тАУ (a₂+b₂)=(a₁тАУa₂)+(b₁тАУb₂)Ваi числа виду , тобто належать до множини K. Отже в множинi K визначенi операцii додавання та множення i здiйсненна обернена додаванню операцiя вiднiмання. Оскiльки операцii додавання i множення дiйсних чисел асоцiативнi й комутативнi, а елементи множини K i дiйснi числа, то операцii додавання i множення елементiв множини K також асоцiативнi й комутативнi. З цiii ж причини в множинi K операцiя множення дистрибутивна вiдносно операцii додавання. Отже, множина i комутативне кiльце.

До цього кiльця належать, зокрема, всi рацiональнi числа (при b=0), а також число (при а=0, b=1). В цьому прикладi замiсть числа Ваможна було взятиВаi iншi.

№5 Множина, що складаiться з одного числа 0, очевидно, i кiльце. Це кiльце називають нульовим.

Означення Пiдмножина K´ кiльця K називаiться його пiдкiльцем, якщо вона сама утворюi кiльце вiдносно визначених в K операцiй.

Теорема (критерiй пiдкiльця) K´ тАУ пiдкiльце кiльця K тодi i тiльки тодi, коли K´ÌK i "a, b [a, bÎK´Þ(aВ±b)ÎK´ÙabÎK´].

Означення Характеристикою кiльця K з одиницею називають найменше натуральне число n, для якого справджуiться рiвнiсть

ne=0

Якщо це можливо лише коли n=0, то говорять, що кiльце K маi нульову характеристику.

Зрозумiло, що всi числовi кiльця мають нульову характеристику.

Наведемо приклад кiльця, яке маi ненульову характеристику:

Z₄={}, 4В·=, n=4.

Теорема Якщо кiльце K маi характеристику n, то для будьтАУякого aÎK справджуiться рiвнiсть na=0.

Доведення

ne=0 за умовою

na=n(ea)=(ne) a=0a=0.

Доведено.

Означення Комутативне кiльце з одиницею e, в якому немаi дiльникiв нуля називаiться областю цiлiсностi.

Задачi

№1

На множинi R заданi операцii:

aÅb=a+b+1,

aÄb=a+b+ab,

де +, ž звичайнi арифметичнi операцii. Довести, що алгебра (R,Å,Ä), буде областю цiлiсностi.

Доведення.

Властивостi кiльця перевiряються безпосередньою перевiркою. Перевiримо дистрибутивнiсть

(aÅb)Äc=aÄcÅaÄb.

Нехай A=(aÅb)Äc, B=aÄcÅaÄb, тодi

A=(aÅb)Äc=(a+b+1)Äc=a+b+1+c+ac+ab+c=a+b+2c+ac+bc+1,

B=aÄcÅaÄb=(a+c+ac)+(b+c+bc)=a+c+ac+b+c+bc+1=a+b+2c+ac+bc+1,

Отже, A=B.

Перевiримо iснування нульового елемента

aÅq=a,

a+q+1=a,

q=тАУ1 тАУ нульовий елемент.

Перевiримо iснування симетричного елемента

aÅã=q,

a+ã+1=тАУ1,

ã=тАУ2-a тАУ протилежний елемент.

Отже, алгебра (R,Å,Ä) буде комутативним кiльцем. Тепер зтАЩясуiмо наявнiсть одиницi.

aÄe=a

a+e+ae=a,

e (1+a)=0,

e=0 тАУ одиничний елемент.

ЗтАЩясуiмо чи iснують дiльники 0.

aÄb=тАУ1, a≠тАУ1, b≠тАУ1,

a+b+ab=тАУ1,

a+1+b (a+1)=0,

(a+1) (1+b)=0.

Оскiльки a≠тАУ1, b≠тАУ1 i a, bÎR, то дiльникiв нуля немаi.

Це означаi, що K тАУ область цiлiсностi.

Доведено.

№2

Довести, що множина Z[] усiх чисел виду a+b, де a i b тАУ цiлi числа, i кiльцем вiдносно звичайних операцiй додавання i множення.

Доведення.

Застосуiмо прийом, який даi змогу скоротити процес доведення. Якщо треба довести, що деяка непорожня множина K₁ i кiльцем, то ii помiщають (якщо це можливо) в якесь вiдоме кiльце K. Тодi треба лише довести, що K₁ i пiдкiльце кiльця K, звiдки випливаi, що K₁ тАУ кiльце.

Оскiльки Z[] i пiдмножиною, наприклад, кiльця всiх дiйсних чисел R, то доведемо, що Z[] тАУ пiдкiльце кiльця R. Застосуiмо критерiй пiдкiльця.Насамперед, покажемо, що Z[]≠Ø. Це справдi так, бо, наприклад, 0=0+0ÎZ[]. Нехай тепер t=a+b, s=c+d, де a, b, c, d ÎZ, t, s ÎZ[].

Покажемо, що (t+s)ÎZ[], (tтАУs)ÎZ[], tsÎZ[].

Справдi, tВ±s=(a+b)В±(c+d)=(aВ±c)+(bВ±d)ÎZ[], оскiльки (aВ±с)ÎZ, (bВ±d)ÎZ. Аналогiчно для добутку дiстанемо ts=(a+b)В±(c+d)=(ac+3bd)+(ad+bc)ÎZ[], оскiльки для цiлих чисел a, b, c, d, 3 маiмо ac, 3bd, ad, bcÎZ.

Отже, Z[] тАУ пiдкiльце кiльця дiйсних чисел R, а тому Z[] тАУ кiльце.

Доведено.

2. РЖдеали кiльця

2.1 Поняття iдеалу

В теорii подiльностi цiлих чисел, а також в загальнiй теорii подiльностi в кiльцях, важливу роль вiдiграi теорема про можливiсть i однозначнiсть розкладу елемента (числа) в добуток простих множникiв. Виявляiться в деяких кiльцях розклад елемента на добуток простих множникiв не однозначний.

Наприклад, 60=2В·30=6В·10, а 2, 6, 30, 10 тАУ простi елементи в Z₂

Один i той же елемент в рiзних кiльцях може бути простим i складеним.

Наприклад, 17 в Z[i] тАУ складене 17=(4-i) (4+i).

Щоб зтАЩясувати, в яких кiльцях справджуiться загальна теорема про iснування i iдинiсть розкладу елемента в добуток простих множникiв, треба узагальнити поняття подiльностi елементiв, що робиться за допомогою iдеалу.

Означення Непорожня множина I кiльця K називаiться його iдеалом, якщо вона замкнена вiдносно вiднiмання i множення на довiльний елемент кiльця.

Переконаiмося, що iдеал РЖ замкнений вiдносно операцii додавання. Справдi iз замкнутостi вiдносно операцii вiднiмання випливаi, що 0ÎА (атАУа=0), тАУ еÎРЖ i поряд з кожним bÎI I'(тАУb) тАУ b=тАУeb. Тому з кожним елементом aтАУb мiстить a тАУ (тАУb)=a+b. (a+b)ÎI.

Звiдси випливаi, що iдеал РЖ кiльця К i його пiдкiльцем. Проте не всяке пiдкiльце кiльця буде його iдеалом.

Розглянемо деякi приклади:

№1 КтАУiдеал самого себе. Цей iдеал називаiться одиничним. Позначаiться РЖ_е.

№2 Кожне кiльце мiстить пiдкiльце {0}, яке теж буде iдеалом кiльця К. Цей iдеал називаiться нульовим. Позначаiться РЖ₀.

РЖ_е та РЖ₀ тАУ тривiальнi iдеали. В розумiннi вiдношення включення РЖ_е тАУ найбiльший, а РЖ₀ тАУ найменший серед усiх iдеалiв кiльця.

Означення РЖдеал РЖ кiльця К називаiться головним, якщо вiн складаiться з усiх елементiв ка кiльця К, аÎК, кÎК. Говорять, що вiн породжений елементом а. Позначають (а).

Наприклад, iдеал Z₂ кiльця Z буде головним, вiн породжений елементом 2 або тАУ2.

2.1 Операцii над iдеалами

Теорема Перетин ab iдеалiв a, bÎK i iдеалом кiльця K.

Доведення.

З того, що a, bÎI₁ÇI₂ випливаi, що abÎI₁, abÎI₂. Так як I₁ та I₂ тАУiдеали, то (aтАУb)ÎI₁, (aтАУb)ÎI₂ Þ (aтАУb)ÎI₁ÇI₂. aÎI₁ÇI₂ Þ aÎI₁, aÎI₂.

kÎK Þ kaÎI₁, kaÎI₂, kaÎI₁ÇI₂.

Отже, I₁ÇI₂ÎK.

Доведено.

Слiд зауважити, що обтАЩiднання iдеалiв не завжди буде iдеалом кiльця. Ця властивiсть поширюiться на перетин n iдеалiв.

Операцii додавання й множення пiдмножин кiльця можна, звичайно, застосувати до iдеалiв.

Означення Сумою iдеалiв I₁, I₂ кiльця K називаiться множина I₁+I₂, яка визначаiться рiвнiстю

I₁+I₂ ={a+bï aÎI₁, bÎI₂}.

Означення Добуток iдеалiв I₁I₂ кiльця К теж буде iдеалом кiльця К.

Нехай а i b тАУ довiльнi iдеали кiльця К.

Теорема2. Сума а + b iдеалiв a i кiльця К i iдеал цього кiльця.

Доведення.

Справдi, сума (а₁ +b₁) + (a₂+ b₂) будь-яких двох елементiв a₁+b₁ i a₂+b₂ множини a+b належить до a+b, оскiльки (a₁+a₂)Îa, (b₁+b₂)Î , i елемент тАУ (а+b) = (тАУа) + (тАУb), протилежний довiльно вибраному елементу (a+b)Î(a+b), також належить до a+b, бо (тАУa)Îa, (тАУb)Î.

Отже, а + b i пiдгрупа адитивноi групи кiльця K. Крiм того, для будь-яких елементiв a+bÎa+b i хÎK x (a+b)=xa+xbÎa+b i (a+b) x=ax+bxÎa+b.

Цим теорему доведено.

Теорема 3. Добуток ab iдеалiв а i кiльця К. також i iдеал кiльця К.

Доведення.

Справдi, сум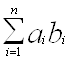а Ва+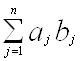Вабудь-яких двох елементiв множини аb i, очевидно, елемент цiii самоi множини, i елемент 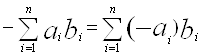, протилежний довiльно вибраному елементу 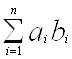Îab, належить до ab. Крiм того, для будь-яких

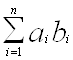Îab i xÎK 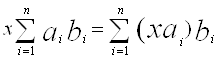Î ab й 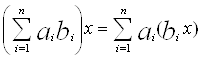ВаÎ ab.

Цим теорему доведено.

Таким чином, у множинi iдеалiв кiльця К здiйсненнi операцii додавання й множення. Операцiя додавання iдеалiв тАУ асоцiативна i комутативна, а операцiя множення тАУ асоцiативна. Якщо кiльце К тАУ комутативне, то операцiя множення iдеалiв також комутативна.

Задачi

№1

Нехай K₁ тАУ пiдкiльце кiльця K. Довести, що K₁ÇI тАУiдеал кiльця K₁.

Доведення.

Введемо позначення D=K₁ÇI. Покажемо спочатку, що iдеал I, як i будьтАУякий iдеал, мiстить нультАУелемент кiльця K. Справдi, оскiльки I≠Ø, то в I iснуi хоч один елемент а. Тодi згiдно з першим пунктом означення iдеалу, елемент атАУа, тобто 0, теж належить iдеалу I. Оскiльки 0ÎK₁, 0ÎI, то 0ÎD i тому D≠Ø.

Якщо a, bÎD, то a, bÎK₁ i a, bÎI. Згiдно з означенням iдеалу i критерiiм пiдкiльця, aВ±bÎI, aВ±bÎK₁, а тому aВ±bÎD.

Нехай aÎD, bÎK₁. Покажемо, що ab i ba належать D. Справдi, оскiльки DÍK₁, то a, bÎK₁ i за критерiiм пiдкiльця K₁ маiмо, що

ab, ba ÎK₁. (1)

Оскiльки DÍI, а I тАУ iдеал кiльця K, то для будьтАУякого елемента aÎDÍI i будьтАУякого елемента bÎK₁ÎK маiмо, що

ab, baÎI. (2)

З включень (1) i (2) випливаi, що

ab, baÎK₁ÇI=D.

Отже, D=K₁ÇI тАУiдеал кiльця K₁.

Доведено.

№2

Чи i iдеалом (лiвим або правим) така пiдмножина

в кiльцi M (2, Z).

РозвтАЩязання

Перевiримо чи буде множина S лiвим iдеалом

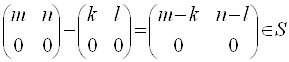
Перевiримо множення з лiва

Отже, дана пiдмножина лiвим iдеалом кiльця M (2, Z).

Перевiримо чи буде правим iдеалом

Отже правим iдеалом буде.

Вiдповiдь: i правим iдеалом.

3. Факторiальнi кiльця

3.1 Кiльця головних iдеалiв та евклiдовi кiльця

3.1.1 Подiльнiсть в областi цiлiсностi

В теорii кiлець особливоi уваги заслуговують кiльця, якi за своiми властивостями досить близькi до кiльця цiлих чисел. Зокрема, для цих кiлець можна розвинути теорiю подiльностi, аналогiчну теорii подiльностi цiлих чисел. Цi кiльця дiстали назву кiлець головних iдеалiв. Вивченням iх ми i будемо займатись. Але спочатку викладемо деякi загальнi вiдомостi, що стосуються подiльностi в областi цiлiсностi з одиницею.

Нехай R тАУ область цiлiсностi з одиницею. Оскiльки область цiлiсностi тАУ комутативне кiльце, то в нiй поняття правого i лiвого дiльника елемента збiгаються i тому означення подiльностi формулюiться так:

Означення 1. Якщо для елементiв а i b областi цiлiсностi R в R iснуi такий елемент с, що а == bс, то говорять, що а дiлиться на b або b дiлить а i пишуть вiдповiдно аM b; b/а або а == 0 (mod b).

Як бачимо, означення 1 i поширенням на область цiлiсностi означення подiльностi в кiльцi цiлих чисел, яке i конкретним прикладом областi цiлiсностi.

З означення 1 випливають такi властивостi подiльностi в областi цiлiсностi:

1. "(a, b, cÎR) [aM bÙbM cÞaM c].

2. "(a, b, cÎR) [aM cÙbM cÞ(a+b)M c Ù(a-b)M c].

3. "(a, b, cÎR) [aM b Þ acM b].

4. "(a_1, b_1, a_2, b_2,тАж, a_n, b_n, cÎ R) [a₁ M cÙa₂ M c ÙтАж Ùa_nM c Þ (a₁b₁ +a₂ b₂ + тАж + +a_n b_n) M c].

Цi властивостi, як легко бачити, i поширенням на область цiлiсностi вiдповiдних властивостей подiльностi в кiльцi цiлих чисел.

5. Кожен елемент аÎ R дiлиться на будь-який дiльник ε одиницi е. Справдi, а = ε (ε^-1а) i, отже, ε/а.

6. Якщо а Î R дiлиться на bÎ R, то а дiлиться i на bε, де ε тАУ будь-який дiльник одиницi.

Справдi, з рiвностi а = bс випливаi рiвнiсть а == bε (ε^-1с) i, отже, bε/а.

7. Кожен з дiльникiв одного з елементiв а ÎR i aεÎ R де ε тАУ будь-який дiльник одиницi, i дiльником i iншого.

Справдi, з рiвностi а = сg випливаi рiвнiсть aε == с (εg), а з рiвностi аε = сq тАУ рiвнiсть а == с (ε^-1q). Отже, якщо с/а, то с/аε, i навпаки.

Всюди далi будемо розглядати елементи областi цiлiсностi R, вiдмiннi вiд нуля.

Означення 2. Елементи а i b областi цiлiсностi R називаються асоцiйованими, якщо кожен з них i дiльником iншого:

а = bс, b= аd. (1)

З рiвностей (1) випливаi, що а = а (сd). Звiдси, скоротивши обидвi частини рiвностi на а≠0, дiстаiмо сd = 1. Отже, с i d i дiльники одиницi. Таким чином, якщо а i b тАУ асоцiйованi елементи, то b = аε, де ε тАУ деякий дiльник одиницi. З другого боку, який би ми не взяли дiльник одиницi ε, елементи а i аε асоцiйованi мiж собою, оскiльки а = (аε) ε^-1.

Означення 2'. Елементи а i b областi цiлiсностi R називаються асоцiйованими, якщо b= аε, де ε тАУ деякий дiльник одиницi.

В кiльцi цiлих чисел, наприклад, асоцiйованими i кожнi два числа т i тАУ т.

Якщо а i b тАУ асоцiйованi елементи, тобто а = bс i b = аd, то (а) Í (b) i (b) Í (а) i, отже, (а) = (b).

Таким чином, два асоцiйованi елементи а i b породжують той самий головний iдеал.

Нехай а i b тАУ довiльнi елементи областi цiлiсностi R.

Означення 3. Елемент сÎR називаiться спiльним дiльником елементiв а i b, якщо кожен з цих елементiв дiлиться на с. За властивiстю 5, всi дiльники одиницi е областi цiлiсностi R i спiльними дiльниками елементiв а i b. Але в елементiв а i b можуть бути й iншi спiльнi дiльники. Ми хочемо ввести поняття найбiльшого спiльного дiльника цих елементiв. Означення НСД двох цiлих чисел, за яким найбiльшим спiльним дiльником називають найбiльший iз спiльних дiльникiв, поширити на область цiлiсностi не можна, оскiльки в довiльнiй областi цiлiсностi R немаi вiдношення порядку. Проте ми знаiмо й iнше означення НСД двох чисел, а саме: НСД двох чисел називають такий спiльний дiльник цих чисел, який дiлиться на будь-який iнший iхнiй спiльний дiльник. Саме це означення ми й поширимо на область цiлiсностi.

Означення 4. Найбiльшим спiльним дiльником елементiв а i b областi цiлiсностi R називаiться такий спiльний дiльник цих елементiв, який дiлиться на будь-який iнший iхнiй спiльний дiльник.

Щоб зазначити, що d i найбiльший спiльний дiльник елементiв а i b, пишуть а=(а, b).

Якщо також d' = (а, b), то елементи d i d' дiляться один на одного i, отже, вони асоцiйованi. З другого боку, якщо d = (а, b) i ε тАУ будь-який дiльник одиницi, то, очевидно, dе = (а, b). Як бачимо, найбiльший спiльний дiльник елементiв а i b визначаiться з точнiстю до множника ε, що i дiльником одиницi.

Означення 5. Елементи а, bÎR називаються взаiмно простими, якщо вони не мають спiльних дiльникiв, вiдмiнних вiд дiльникiв одиницi, тобто якщо (а, b) = 1.

Нехай ε тАУ будь-який дiльник одиницi i а тАУ довiльний елемент областi цiлiсностi R. Тодi а = аεтАв ε^-1. З цiii рiвностi випливаi, що всi елементи, асоцiйованi з елементом а, i всi дiльники одиницi ε дiльниками елемента а. РЗх називають тривiальними, або невласними, дiльниками елемента а. Всi iншi дiльники елемента а, тобто дiльники, вiдмiннi вiд аε i ε, якщо такi iснують, називають нетривiальними, або власними. Так, в кiльцi цiлих чисел Z тривiальними дiльниками числа 10 i числа В±1, В±10 i нетривiальними тАУ числа В±2, В±5.

Означення 6. Елемент аÎR називаiться нерозкладним, або простим, якщо вiн не i дiльником одиницi й не маi нетривiальних дiльникiв; елемент аÎR називаiться розкладним, або складеним, якщо вiн маi нетривiальнi дiльники.

РЖнакше кажучи, елемент аÎR називаiться розкладним, якщо його можна записати у виглядi добутку а = bс двох нетривiальних множникiв b i с; вiн називаiться нерозкладним, якщо його не можна записати у виглядi добутку двох нетривiальних дiльникiв, тобто якщо з а = bс завжди випливаi, що один з множникiв b i с i дiльник одиницi, а iнший тАУ асоцiйований з а. Так, у кiльцi цiлих чисел Z нерозкладними i числа В±2, В±3, В±5,тАж (тобто числа простi й протилежнi простим); всi iншi числа, вiдмiннi вiд В±1, тАУ розкладнi.

Наведемо такi двi властивостi нерозкладних елементiв.

1. Якщо елемент рÎR нерозкладний, то i будь-який асоцiйований з ним елемент рε також нерозкладний. Ця властивiсть випливаi з властивостi 7 подiльностi елементiв областi цiлiсностi R.

2. Якщо а тАУ будь-який, а р тАУ нерозкладний елемент з R, то або а дiлиться на р, або а i р тАУ взаiмно простi.

Справдi, якщо (а, р) = d, то d, як дiльник нерозкладного елемента р, або i деякий дiльник ε одиницi, або елемент вигляду рε. У першому випадку а i р взаiмно простi, в другому тАУ а дiлиться на р.

Задачi

№1

Довести, що (-8+3)M (1+2) в кiльцi z [].

Доведення.

Подiлимо цi гаусовi числа, домноживши чисельник i знаменник частки на число спряжене iз знаменником

.

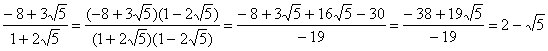Так як 2тАУÎZ[], то (-8+3)M (1+2).

Доведено.

№2

Довести, що в областi цiлiсностi К елементи 25тАУ17Ваi 7-Ваасоцiйованi, якщо К=z[].

Доведення.

Асоцiйованiсть доводиться тим, що одне число дiлиться на друге i навпаки.

ВаОскiльки 3тАУ2Î Z[], то (25тАУ17)M(7-).

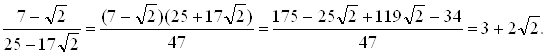
Бачимо, що i (7-)M(25тАУ17).

Отже, данi елементи асоцiйованi.

Доведено.

№3

Довести, що характеристикою областi цiлiсностi i або нуль, або просте число.

Доведення.

Нехай K тАУ область цiлiсностi, а е тАУ одиниця кiльця К. Якщо me≠0 для жодного натурального числа m₁, то характеристика кiльця K дорiвнюi нулю.

Нехай тепер me=0 i m найменше натуральне число, що маi цю властивiсть, тобто m тАУ характеристика кiльця K. Тодi m≠1, оскiльки е≠0. Якщо m просте число, то твердження задачi доведено.

Нехай m складене число. Тодi iснують натуральнi числа s i t такi, що 1

0=me=(st) e=(se) (te).

Крiм того, оскiльки m тАУ характеристика кiльця K i s

Тому характеристикою областi цiлiсностi i або нуль, або просте число.

Доведено.

3.1.2 Кiльце головних iдеалiв

Перейдемо тепер до вивчення кiлець головних iдеалiв.

Означення. Кiльцем головних iдеалiв називаiться область цiлiсностi з одиницею, в якiй кожен iдеал i головний.

Найпростiшим прикладом кiлець головних iдеалiв i кiльце цiлих чисел Z: кiльце Z, як вiдомо, i область цiлiсностi з 1 i, за теоремою, кожен його iдеал головний.

Кожне поле Р i кiльце головних iдеалiв. Справдi, поле Р i областю цiлiсностi з одиницею; якщо U i ненульовий iдеал поля Р, то разом з будь-яким своiм елементом а ≠ 0 вiн мiстить i елемент аa^-1 = 1 i, отже, U = (1). Кiльцем головних iдеалiв i також кiльце многочленiв вiд змiнноi х з коефiцiiнтами з поля Р.

Звичайно, не кожна область цiлiсностi з одиницею i кiльцем головних iдеалiв. Нижче ми наведемо приклади таких областей цiлiсностi. А тепер займемося вивченням властивостей кiлець головних iдеалiв. Всюди далi вважатимемо, що R тАУ кiльце головних iдеалiв.

Теорема 1. Будь-якi два елементи а i b кiльця головних iдеалiв R мають найбiльший спiльний дiльник d, причому d= rа + sb, де r i s тАУ деякi елементи кiльця R.

Доведення.

Якщо один з елементiв а i b дорiвнюi нулю, то справедливiсть теореми очевидна. Нехай а i b тАУ будь-якi вiдмiннi вiд нуля елементи кiльця R. Вони породжують iдеал (а, b), який складаiться з усiх елементiв вигляду ха + уb, де х i у тАУ будь-якi елементи кiльця R. Оскiльки R тАУ кiльце головних iдеалiв, то iдеал (а, b) i головний, тобто породжуiться деяким елементом dÎR: (а, b) = (d).

Тому

d = rа + sb (r, sÎR), (2)

а = gd, b = hd (g, hÎR). (3)

З рiвностей (3) випливаi, що d i спiльний дiльник елементiв а i b;

з рiвностi ж (2) випливаi, що d дiлиться на будь-який спiльний дiльник елементiв а i b. Отже, а = (а, b).

Доведено.

Спираючись на теорему 1, доведемо твердження, яке i критерiiм взаiмноi простоти двох елементiв кiльця головних iдеалiв.

Теорема 2. Елементи а i b кiльця головних iдеалiв R взаiмно простi тодi i тiльки тодi, коли в кiльцi R i такi елементи r i s, що rа +sb = 1.

Доведення.

Необхiднiсть умови очевидна: якщо а i b тАУ взаiмно простi, тобто (а, b) = 1, то, за теоремою 1, в кiльцi R iснують такi елементи r i s, що rа + sb = 1. Доведемо достатнiсть умови. Припустимо, що в кiльцi R iснують такi елементи r i s, що rа + sb = 1.

З цiii рiвностi випливаi, що спiльними дiльниками елементiв а i b можуть бути лише дiльники одиницi i, отже, елементи а i b взаiмно простi.

Доведено.

Теорема 3. Якщо елемент аÎR взаiмно простий з кожним iз елементiв bÎR i сÎК, то вiн взаiмно простий i з добутком цих елементiв.

Доведення.

Оскiльки а i b тАУ взаiмно простi, то, за теоремою 2, iснують такi r, sÎR, що

rа + sb = 1.

Помноживши цю рiвнiсть на с, дiстаiмо: а (rc) + (bс) s = с. З цiii рiвностi випливаi, що кожен спiльний дiльник елементiв а i bс буде дiльником i елемента с. Але за умовою теореми спiльними дiльниками елементiв а i с i лише дiльники одиницi, тому i спiльними дiльниками a i bс будуть лише дiльники одиницi й, отже, а i bс взаiмно простi.

Теорема 4. Якщо добуток елементiв aÎR i bÎR дiлиться на елемент с ÎR, але а i с взаiмно простi, то b дiлиться на с.

Доведення.

Оскiльки а i с тАУ взаiмно простi, то в кiльцi R iснують такi r i s, що

rа + sc = 1.

Помноживши цю рiвнiсть на b, дiстаiмо:

(аb) r+с (bs) = b.

Обидва доданки лiвоi частини останньоi рiвностi дiляться на с, а тому i права ii частина b дiлиться на с.

Теорема 5. Якщо елемент а ÎR дiлиться на кожен з елементiв bÎR i сÎR, якi мiж собою взаiмно простi, то а дiлиться i на добуток bс.

Доведення.

Справдi, за умовою теореми, а.^: b, тобто а = bg. Оскiльки а M с, то bgM с. Але b i с взаiмно простi, тому, за теоремою 4, g: с, тобто g=cq.

Отже, а == (bс) q, тобто аMbс.

Доведено.

Теорема 6. Якщо R тАУ кiльце головних iдеалiв i р тАУ простий елемент цього кiльця, то фактор-кiльце R/(р) i поле.

Доведення.

Одиничний елемент Ва= 1 + (р) кiльця R/(р) вiдмiнний вiд Ва= (р). Справдi, якби = , то елемент 1 мiстився б в iдеалi (р) i тому р/1. Але елемент р не може бути дiльником одиницi, оскiльки вiн нерозкладний. Отже, в кiльцi R/(р) i принаймнi один вiдмiнний вiд нуля елемент.

Покажемо, що в кiльцi R/(р) здiйсненна операцiя дiлення, крiм_дiлення на нуль, тобто що для будь-яких елементiв Ва= a + (р) ≠ 0 i =Ва+ (р) кiльця R/(р) рiвняння тАв Ва= Вамаi в цьому кiльцi розв'язок. Справдi, оскiльки ≠, то а не дiлиться на р. Отже, за другою властивiстю нерозкладних елементiв, елементи а i р тАУ взаiмно простi, тобто (а, р) = 1. Тому, за теоремою 2, в кiльцi R iснують такi елементи r i s, що аr + рs = 1. Звiдси

аrb + рsb =b, аrb º b (тоd p),

i, отже, тАв = . Таким чином, =Ваi розв'язком рiвняння =.

Доведено.

Наслiдок. Якщо добуток кiлькох елементiв кiльця головних iдеалiв R дiлиться на простий елемент рÎR, то принаймнi один iз спiвмножникiв дiлиться на р.

Доведення.

Припустимо, що добуток a₁ тАв а₂ тАвтАж тАв a_s (a_iÎR) дiлиться на нерозкладний елемент р ÎR, тобто що a₁а_2тАж а_s Î (р).

Розглянемо елементи a_i = а_i+(р) (i =1, 2,тАж. s) i = a₁ a₂ тАжa_s+(р). За означенням операцii множення в кiльцi R/(р) =Оскiльки a₁ a₂ тАжa_sÎ(р), то =Ваi, отже, = ВаЗвiдси, оскiльки, за теоремою 6, R/(р) i поле, випливаi, що для деякого m (1 < т < s) =. Але =означаi, що a_mÎ(p), тобто що a_m M р.

Цим справедливiсть наслiдку доведено.

Нашою метою буде тепер доведення твердження про можливiсть розкладу кожного елемента кiльця головних iдеалiв у добуток простих (нерозкладних) множникiв. Воно ТСрунтуiться на такiй лемi.

Лема. В кiльцi головних iдеалiв R не iснуi нескiнченноi строго зростаючоi послiдовностi iдеалiв

U₀Ì U₁Ì U₂ ÌтАжÌU_NÌ тАж. (4)

Доведення.

Припустимо, що нескiнченна строго зростаюча послiдовнiсть (4) iснуi. Позначимо символом b об'iднання всiх iдеалiв послiдовностi (4). Множина b i iдеал кiльця R. Справдi, якщо ai i bi, то а i елемент деякого iдеалу U_s, i b тАУ деякого iдеалу U_l. Тому а i b i елементи iдеалу U_m, де m тАУ бiльший з iндексiв s i l. Отже, (а + b)i U_mÌ, (а тАУ b)iU_mÌ i для будь-якого riR ariU_mÌ. Оскiльки R тАУ кiльце головних iдеалiв, то iдеал b головний. Нехай b= (b). Елемент b, як елемент об'iднання iдеалiв послiдовностi (4), належить до деякого iдеалу U_k, а отже, i до кожного iдеалу U_i, при i ≥k

Тому (b) = U_k=U_k+1 = U_k+2 =тАж. А це суперечить нашому припущенню.

Доведено.

Теорема7. В кiльцi головних iдеалiв R кожен вiдмiнний вiд нуля елемент, що не е дiльником одиницi, розкладаiться в добуток простих множникiв.

Доведення.

Для кожного простого елемента кiльця R теорема справедлива: для простого елемента добуток, про який говориться в теоремi, складаiться з одного множника. Припустимо, що в кiльцi R i вiдмiнний вiд нуля елемент а, який не можна розкласти в добуток простих множникiв. Елемент а не простий i, отже, а = a₁a₂, де a₁ i a₂ тАУ нетривiальнi дiльники елемента а.

Принаймнi один з елементiв a₁ i a₂ не можна розкласти в добуток простих множникiв, бо в противному разi i елемент а розкладався б у добуток простих множникiв. Не втрачаючи загальностi мiркувань, припустимо, що a₁ не можна розкласти в добуток простих множникiв. Тодi a₁=a₁₁a_12, де a₁₁ та a₁₂тАУнетривiальнi дiльники. Принаймнi один з елементiв a₁₁ та a₁₂ також не можна розкласти в добуток простих множникiв. Нехай цим елементом i a₁₁. Для елемента a₁₁ мiркування повторимо i т.д. Цей процес послiдовного розкладу, очевидно, не може обiрватися. Таким чином, ми дiстанемо нескiнченну послiдовнiсть елементiв

а, a₁, a₁₁, a₁₁₁,тАж, (5)

у якiй кожен наступний член i власним дiльником попереднього.

Якщо a_i+1 i власним дiльником a_i, то (a_i+1)Ì(a_i), оскiльки a_i=a_i+1r, де r тАУ деякий елемент R. Тому головнi iдеали, породженi елементами послiдовностi (5), утворюють нескiнченну строго зростаючу послiдовнiсть iдеалiв

(а)Ì(a₁)Ì(a₁₁)Ì(a₁₁₁)ÌтАж,

а це суперечить доведенiй вище лемi. Отже, наше припущення неправильне.

Доведено.

Покажемо тепер, що розклад, про який iде мова в теоремi 7, однозначний з точнiстю до порядку спiвмножникiв i до дiльникiв одиницi.

Теорема8. Якщо

a =p₁p₂тАжp_r =q₁q₂тАжq_s

i два розклади елемента а кiльця головних iдеалiв R в добуток простих множникiв, то r=s i, при вiдповiднiй нумерацii спiвмножникiв, справджуються рiвностi q_i=ε_i p_i (i == 1, 2,тАж, r), де ε_i тАУ деякий дiльник одиницi кiльця R.

Доведення.

Доводитимемо iндукцiiю по r. При r = РЖ справедливiсть твердження очевидна.

Справдi, оскiльки елемент а = р₁ простий, то добуток q₁q₂тАжq_s

може мiстити лише один множник q₁₌p₁.

Припустимо, що теорема правильна для r тАУ 1 (2 £ r), i доведемо, що в такому разi теорема справедлива й для r. Справдi, оскiльки

a =p₁p₂тАжp_r i a = q₁q₂тАжq_s то

p₁p₂тАжp_r =q₁q₂тАжq_s (6)

З рiвностi (6) випливаi, що q₁q₂тАжq_s дiлиться на p₁. Тому, за наслiдком з теореми 6, принаймнi один iз спiвмножникiв q_1,q_2,тАж, q_s дiлиться на p_i. Ми вважатимемо, що на p₁ дiлиться множник q₁: цього завжди можна досягти змiною нумерацii множникiв q_1,q_2,тАж, q_s. Оскiльки q₁ тАУ простий елемент i дiлиться на простий елемент p₁, то q₁=e₁p₁, де e₁ тАУ деякий дiльник одиницi кiльця R. Пiдставивши в рiвнiсть (6) e₁p₁ замiсть q₁ i скоротивши обидвi частини одержаноi рiвностi на р₁, дiстанемо:

p₂p₃тАжp_r =(e₁q₂) q₃тАжq_s.

Але, за iндуктивним припущенням, rтАУ 1 == sтАУ 1 i при вiдповiднiй нумерацii множникiв q_1,q_2,тАж, q_r:

q₂=e₁q₂=e₂p_2, q₃=e₃p₃, тАж, q_r=e_rp_r,

де e_i тАУ деякi дiльники одиницi кiльця R. Тому r = s i при вiдповiднiй нумерацii множникiв q₁, q₂, тАж, q_r:

q₁=e₁p₁, q₂=e₁^тАУ1e₂p₂ =e₂p_2, q₃=e₃p₃, тАж, q_r=e_rp_r

Доведено.

Зауважимо, що теореми 7 i 8 справедливi, зокрема, для кiльця цiлих чисел, яке i кiльцем головних iдеалiв.

Постаi запитання: чи не можна теореми 7 i 8 поширити на клас областей цiлiсностi бiльш широкий, нiж кiльце головних iдеалiв? Вiдповiдь на це запитання в загальному випадку негативна. РД областi цiлiсностi, в яких не справджуiться теорема про розклад елементiв областi цiлiсностi в добутки простих множникiв, а також областi цiлiсностi, в яких розклад елементiв на простi множники хоч i можливий, але не однозначний. Наведемо приклади таких областей цiлiсностi, не вивчаючи ii докладно.

Нехай К тАУ множина всiх дiйсних чисел виду

де n тАУ будь-яке натуральне число, a_1,a_2,тАж, a_n тАУ будь-якi цiлi числа й r₁, r₂,тАж, r_n тАУ будь-якi числа виду Ва(m, k тАУ цiлi невiд'iмнi числа). Сума, рiзниця й добуток чисел такого виду тАУ числа такого самого виду. Отже, К тАУ кiльце. При п = 1 i r₁=0 дiстанемо с = а₁; тому К мiстить усi цiлi числа, зокрема 1. Легко бачити, що кiльце К i область цiлiсностi. У цiй областi цiлiсностi число 2 розкладаiться на множники так:

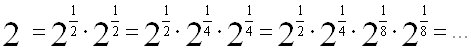
Можна довести, що числа виду

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Аксонометричнi проекцii