Функция многих переменных
Функция многих переменных. Предел и непрерывность функции многих переменных. Частные производные.
План.
1. Определение функции многих переменных.
2.Ва Предел функции многих переменных. Непрерывность функции многих переменных.
3.Ва Частные производные.
1. Обозначим через D некоторое множество точек в п-мерном пространстве.
Если задан законВа fВа, в силу которого каждой точке М(х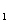 ;..;х
;..;х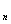 )
)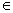 D ставится в соответствие число и, то говорят, что на множестве Dопределена функция и=f(х
D ставится в соответствие число и, то говорят, что на множестве Dопределена функция и=f(х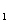 ;..;х
;..;х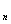 ).
).
Множество точек М(х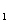 ;..;х
;..;х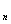 ), для которых функция и=f(х
), для которых функция и=f(х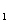 ;..;х
;..;х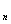 ) определена, называютВа областью определения этой функции и обозначают D(f).
) определена, называютВа областью определения этой функции и обозначают D(f).
Функции многих переменных можно обозначать одним символом и=f(М), указывая размерность пространства, которому принадлежит точка М.
Функции двух переменных можно изобразить графически в виде некоторой поверхности.
Графиком функции двух переменныхВа z=f(х;у) в прямоугольной системе координат Оху называется геометрическое место точек в трехмерном пространстве, координаты которых (х;у;z) удовлетворяют уравнению z=f(х;у).
2. Обозначим через 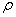 (М;М
(М;М ) расстояние между точками М и М
) расстояние между точками М и М . Если п=2, М(х;у), М
. Если п=2, М(х;у), М (х
(х ;у
;у ), то
), то
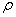 (М;М
(М;М )=
)=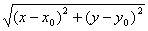 .
.
ВаВаВаВаВа В п-мерном пространстве
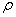 (М;М
(М;М )=
)=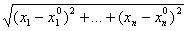 .
.
ВаВаВаВаВа Пусть на множестве Dзадано функцию и=f(М).
ВаВаВаВаВа Число А называется пределом функции и=f(М) в точке М , если для произвольного числа
, если для произвольного числа 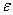 >0 найдётся такое число
>0 найдётся такое число 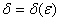 >0, что для всех точек М
>0, что для всех точек М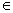 D, которые удовлетворяют условию 0<
D, которые удовлетворяют условию 0<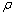 (М;М
(М;М )<
)<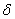 , выполняется неравенство
, выполняется неравенство


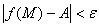 .
.
ВаВаВаВаВа Свойства пределов функций одной переменной сохраняются и для функций многих переменных, то есть если функции f(М) и g(М) имеют в точке М Ваконечные пределы, то
Ваконечные пределы, то
ВаВаВаВаВаВаВаВа 1. 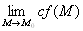 = с
= с ,
,
Ва2. 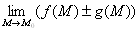 =
=
 ,
,
ВаВаВаВаВаВаВаВа 3. 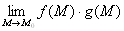 =
=
 .
.
ВаВаВа ВаВаВаВаВа4. 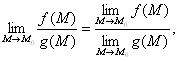 ВаВаесли
ВаВаесли 
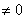 .
.
ВаВаВаВаВаВа Заметим, чтоВа если пределВа  Васуществует, то он не должен зависеть от пути, по которому точка М стремится к точкеВа М
Васуществует, то он не должен зависеть от пути, по которому точка М стремится к точкеВа М .
.
ВаВаВаВаВаВа Функция и=f(М) называется непрерывной в точкеМ , если
, если
 = f(М
= f(М ).
).
ВаВаВаВаВа Функция и=f(М) называется непрерывной на множестве D, если она непрерывна в каждой точке М D.
D.
Точки, в которых непрерывность функции нарушается, называются точками разрыва функция. Точки разрыва могут быть изолированными, создавать линии разрыва, поверхности разрыва и т. д.Например, функцияВа z=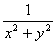 имеет разрыв в точке (0;0), а функцияВа z=
имеет разрыв в точке (0;0), а функцияВа z=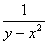 Ваимеет разрыв на параболе
Ваимеет разрыв на параболе 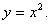
3. Множество точек М, которые удовлетворяют неравенствуВа 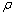 (М;М
(М;М )<
)<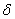 , называют
, называют 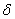 -окрестностью точки М
-окрестностью точки М .
.
ВаВаВаВаВа Пусть функция двух переменныхВа z=f(x;у)Ва (для большего количества переменных всё аналогично) определена в некоторойВа окрестности точки М(x;у). Дадим переменной х приращение 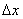 так, чтобы точка (х+
так, чтобы точка (х+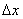 ;у) принадлежала этой окрестности. При этом функцияВа z=f(x;у) изменится на величину
;у) принадлежала этой окрестности. При этом функцияВа z=f(x;у) изменится на величину
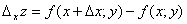 ,
,
которая называется частичным приращением функции z=f(x;у) по переменной х.
Аналогично величину
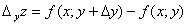
называют частичным приращением функциипо переменной у.
ВаВаВаВаВа Если существует предел
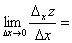
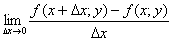 ,
,
то его называют частной производной функции z=f(x;у) в точкеМ(x;у) по переменной х и обозначают такими символами:
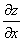 ,
,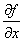 ,
,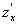 ,
,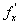 .
.
ВаВаВаВаВа Аналогично
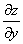 =
= 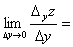
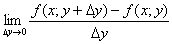 .
.
Ва ВаВаВаВаИз таких определений следует, что правила вычисления производных, совпадают с правилами дифференцирования функций одной переменной. Следует только помнить, что при вычислении частной производной по одной переменной остальные переменные считаются постоянными.
ВаВаВаВаВа Частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей.
ВаВаВаВаВа Частные производные от частных производныхВа 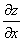 ,
, 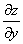 Вафункцииz=f(x;у) называются частными производными второго порядка. Функция двух переменныхВа может иметь четыре частные производные второго порядка, которые обозначают так:
Вафункцииz=f(x;у) называются частными производными второго порядка. Функция двух переменныхВа может иметь четыре частные производные второго порядка, которые обозначают так:
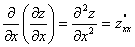 ,ВаВаВаВаВаВаВаВа
,ВаВаВаВаВаВаВаВа 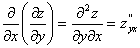 ,
,
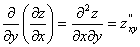 ,ВаВаВаВаВаВаВаВа
,ВаВаВаВаВаВаВаВа 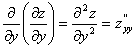 .
.
ВаВаВаВаВа Производные 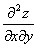 Ваи
Ваи 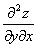 Ваназываются смешанными. Можно доказать, что если они непрерывны, то равны между собой.
Ваназываются смешанными. Можно доказать, что если они непрерывны, то равны между собой.
ВаВаВаВаВа Частные производные от частных производных второго порядка называютсяВа частными производными третьего порядка и т. д.
Лекция 11.Ва Тема тАУ Дифференцируемость функции. Производная в направлении. Градиент. Локальные экстремумы.
План.
1. Дифференцируемость функции. Полный дифференциал. Дифференциалы высших порядков.
2.Ва Производная в направлении. Градиент и его свойства.
3.Ва Локальные экстремумы функции высших порядков.
1. Пусть функцияВа z=f(x;у) непрерывна в некоторой окрестности точки М(x;у) вместе со своими частными производными 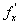 (х;у),
(х;у),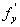 (х;у). Выберем приращение
(х;у). Выберем приращение 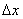 и
и 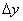 так, чтобы точка (х+
так, чтобы точка (х+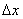 ;у+
;у+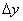 ) принадлежала рассматриваемой окрестности.
) принадлежала рассматриваемой окрестности.
Если полное приращение функцииВа z=f(x;у)Ва в точке М(x;у)
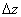 = f(x+
= f(x+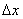 ;у+
;у+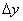 )-f(x;у)
)-f(x;у)
можно записать в виде
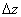 =
=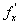 (х;у)
(х;у)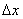 +
+ 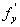 (х;у)
(х;у)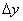 +
+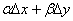 ,
,
где 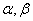 - бесконечно малые функции при
- бесконечно малые функции при 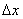
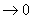 ,
, 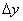
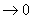 , то функцияВа z=f(x;у) называется дифференцированной в точке М(x;у), а линейная относительно
, то функцияВа z=f(x;у) называется дифференцированной в точке М(x;у), а линейная относительно 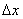 и
и 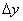 Вачасть её полного приращения
Вачасть её полного приращения 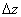 Ваназывается полным дифференциалом функции и обозначается
Ваназывается полным дифференциалом функции и обозначается
dz=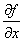
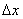 +
+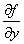
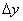 .
.
Дифференциалами независимых переменных называют приращения этих переменных dх=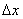 , dу=
, dу=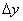 . Поэтому
. Поэтому
dz=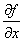 dх +
dх +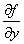 dу,
dу,
или в других обозначениях
dz=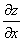 dх +
dх +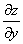 dу.
dу.
Для функции трёх переменных и= f(x;у;z)Ва
dи=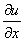 dх +
dх +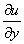 dу+
dу+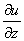 dz.
dz.
Полный дифференциал функцииВа z=f(x;у)
dz=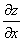 dх +
dх +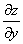 dу,
dу,
который ещё называют дифференциалом первого порядка, зависит от независимых переменных х, у и от их дифференциалов dх, dу. Заметим, что дифференциалы dх, dу не зависят от х, у.
Дифференциалы второго порядка определяют по формуле
d2z= d(dz).
Тогда
d2z= d(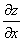 dх+
dх+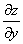 dу)=
dу)= 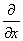 (
(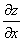 dх+
dх+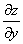 dу)dх+
dу)dх+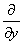 (
(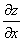 dх+
dх+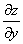 dу)dу=
dу)dу=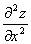 dх2+
dх2+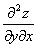 dу dх+
dу dх+
+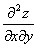 dх dу+
dх dу+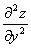 dу2,
dу2,
откуда
d2z=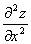 dх2+2
dх2+2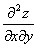 dх dу+
dх dу+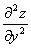 dу2.
dу2.
Символически это можно записать так:
d2z=(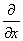 dх+
dх+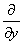 dу)2z.
dу)2z.
Аналогично можно получить формулу для полного дифференциала п-го порядка:
dпz= d(dп-1z) =(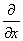 dх+
dх+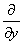 dу)пz.
dу)пz.
2. Производная функцииВа z=f(x;у) в направлении вектора 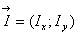 Вавычисляется по формуле
Вавычисляется по формуле
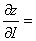
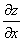
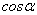 +
+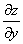
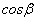 ,
,
где 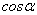 ,
, 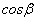 - направляющие косинусы вектора
- направляющие косинусы вектора 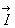 :
:
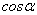 =
= 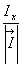 ,ВаВаВа
,ВаВаВа 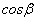 =
= 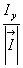 .
.
Если частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей, то производная в направлении вектора 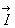 определяет скорость изменения функции в направлении вектора
определяет скорость изменения функции в направлении вектора 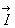 .
.
Градиентом функцииВа z=f(x;у) называется вектор
grad z=(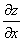 ,
,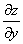 ).
).
Свойства градиента
1. Производная 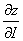 Ваимеет наибольшее значение, если направление вектора
Ваимеет наибольшее значение, если направление вектора 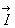 Васовпадает с направлением градиента, причём это наибольшее значение производной равно
Васовпадает с направлением градиента, причём это наибольшее значение производной равно 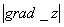 .
.
2. Производная в направлении вектора, перпендикулярного градиенту, равна нулю.
3. Пусть функцияВа z=f(x;у) определена на множестве D и точка М (х
(х ;у
;у )
)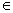 D. Если существует окрестность точки М
D. Если существует окрестность точки М , которая принадлежит множеству D, и для всех отличных от М
, которая принадлежит множеству D, и для всех отличных от М точек М выполняется неравенство
точек М выполняется неравенство
f(М)<f(М0)ВаВаВа (f(М)>f(М0)),
то точку М Ваназывают точкой локального максимума (минимума) функцииВа z=f(x;у), а число f(М0) -Ва локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.
Ваназывают точкой локального максимума (минимума) функцииВа z=f(x;у), а число f(М0) -Ва локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.
Теорема 5.1 (необходимые условия экстремума).Ва ЕслиВа функцияВа z=f(x;у) в точке М ( х
( х ;у
;у ) имеет локальный экстремум, то в этой точке частные производные
) имеет локальный экстремум, то в этой точке частные производные 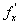 ,
,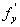 Варавны нулю или не существуют.
Варавны нулю или не существуют.
Точки, в которых 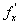 =
=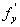 = 0, называются стационарными. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.
= 0, называются стационарными. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.
Поэтому функция может достигать экстремальных значений только в критических точках; однако не всякая критическая точка является точкой экстремума.
Пусть в стационарной точке М ( х
( х ;у
;у ) и некоторой её окрестности функцияВа z=f(x;у) имеет непрерывные частные производные второго порядка. Введём обозначения:
) и некоторой её окрестности функцияВа z=f(x;у) имеет непрерывные частные производные второго порядка. Введём обозначения:
А=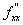 ( х
( х ;у
;у ),Ва В=
),Ва В=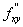 ( х
( х ;у
;у ),Ва С=
),Ва С=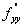 ( х
( х ;у
;у ),Ва
),Ва  =АС-В2.
=АС-В2.
Теорема 5.2 (достаточные условия экстремума).Ва
1. Если  >0, то функцияВа z=f(x;у) в точке М
>0, то функцияВа z=f(x;у) в точке М Ваимеет экстремум, причём максимум при А<0 и минимум при А>0.
Ваимеет экстремум, причём максимум при А<0 и минимум при А>0.
2. Если  <0, то в точке М
<0, то в точке М Ванет экстремума.
Ванет экстремума.
Для случая, когда количество переменных п>2, пользуются такой теоремой.
Теорема 5.3Ва Функция и=f(х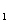 ;..;х
;..;х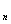 ) имеет минимум в стационарной точке М
) имеет минимум в стационарной точке М , если дифференциал второго порядка этой функции в точке М
, если дифференциал второго порядка этой функции в точке М Ваположителен d2f(М
Ваположителен d2f(М )>0, и максимум, еслиВаd2f(М
)>0, и максимум, еслиВаd2f(М )<0.
)<0.
Пример. Исследовать на экстремум функцию
z=(х+2)2+(у -1)2.
Решение.
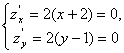

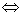
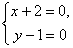
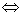
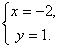
Функция имеет одну критическую точку М(-2;1).
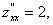
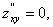
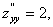 А=2,Ва В=0,Ва С=2,
А=2,Ва В=0,Ва С=2,
 =АС-В2= 2*2-02= 4>0,Ва А>0.
=АС-В2= 2*2-02= 4>0,Ва А>0.
Значит, в точке М(-2;1) функция имеет минимум: min z=z(-2;1)=(-2+2)2+(1-1)2=0.
Лекция 12.Ва Тема тАУ Интегральное исчисление функций. Первообразная. Неопределённный интеграл. Методы интегрирования.
План.
1. Первообразная функции. Неопределённный интеграл. Свойства неопределённого интеграла.
2.Ва Таблица основных интегралов. Метод подстановки (замены переменной).
3.Ва Интегрирование по частям. Интегралы, которые тАЭне берутсятАЭ.
Интеграл тАУ одно из центральных понятий математики. Оно возникло в связи с двумя задачами: 1) о восстановлении функции по её производной; 2) о вычислении площади криволинейной трапеции. Эти задачи приводят к двум связанным между собой видам интегралов: определённого и неопределённого. Термин тАЭинтегралтАЭ ввёл Якоб Бернулли в 1690 году.
1. Функция F(x) называется первообразной функции f(x) на некотором промежутке, если во всех точках этого промежутка выполняется равенство FтАЩ(x)=f(x).
Например. первообразными функцииf(x)=3х2 будут функции х3, х3+1, х3+0,5 и вообще F(x)= х3+С, где С тАУ произвольная постоянная, поскольку FтАЩ(x)=( х3+С)тАЩ=3х2. Этот пример показывает, что если функцияf(x) имеет одну первообразную, то она имеет их бесконечно много. Возникает вопрос: как найти все первообразные данной функции, если известна одна из них? Ответ даёт такая теорема.
Теорема 6.1 ЕслиВа F(x) тАУ первообразная функцииf(x) на некотором промежутке, то всякая другая первообразная функцииf(x) на этом промежутке имеет вид F(x) +С, где С тАУ произвольная постоянная.
Множество всех первообразных F(x) +С функцииf(x) называют неопределённым интегралом функции f(x) и обозначают 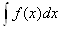 . Таким образом, по определению
. Таким образом, по определению
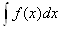 =F(x) +С,ВаВа еслиВаВаВа FтАЩ(x)=f(x).
=F(x) +С,ВаВа еслиВаВаВа FтАЩ(x)=f(x).
При этомВа f(x) называют подынтегральной функцией,Ва f(x)dх тАУ подынтегральным выражением, х тАУ переменной интегрирования, знак 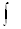 - знаком интеграла, С тАУ постоянной интегрирования.
- знаком интеграла, С тАУ постоянной интегрирования.
Операцию нахождения первообразной функцииf(x) называют интегрированием этой функции.
Операции дифференцирования и интегрирования являются обратными по отношениюВа друг кВа другу.
Возникает вопрос: для каждой ли функцииf(x) существует первообразная, а значит, и неопределённый интеграл? Оказывается не для каждой. Но справедлива такая
Теорема 6.2. Всякая непрерывная на промежутке [a;b] функция имеет на этом промежутке первообразную.
СВОЙСТВА НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. (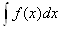 )тАЩ=f(x).
)тАЩ=f(x).
2. 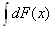 =F(x) +С.
=F(x) +С.
3. d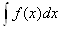 = f(x)dх.
= f(x)dх.
4. 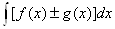 =
=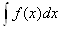
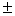
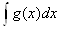 .
.
5. Если 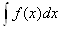 =F(x) +С и и=
=F(x) +С и и=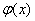 - произвольная функция, которая имеет непрерывную производную, то
- произвольная функция, которая имеет непрерывную производную, то
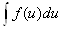 =F(и) +С.
=F(и) +С.
В частности,
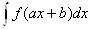 =
=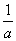 F(ax+) +С.
F(ax+) +С.
Из очень важного свойства 5 следует, что таблица интегралов остаётся верной независимо от того, является ли переменная интегрирования независимой переменной или произвольной дифференцированной функцией. Таким образом, из одной формулы можно получать много других.
Пример.
 =
=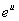 +С
+С 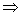
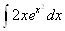 =
=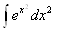 =
=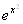 +С,
+С, 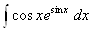 =
=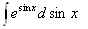 =
=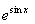 +С,
+С, 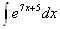 =
=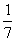
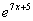 +С.
+С.
2. ВаВаТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
1. 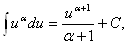
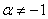 .
.
2. 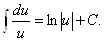
3. 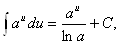 а>0,ВаВа
а>0,ВаВа 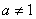 .
.
4. 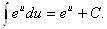
5. 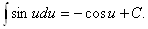
6. 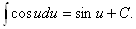
7. 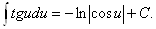
8. 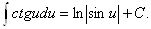
9. 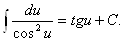
10. 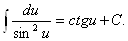
11. 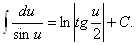
12. 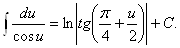
13. 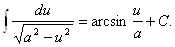
14. 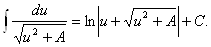
15. 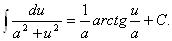
16. 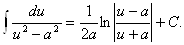
17. 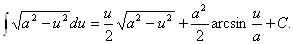
18. 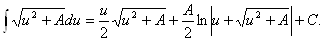
Непосредственным интегрированием называют вычисление интегралов с помощью основных свойств неопределённого интеграла и таблицы интегралов.
Пример.
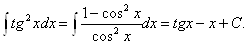
Метод подстановки является одним из основных методов интегрирования. Больше того, изучение методов интегрирования в основном сводится к выяснению того, какую подстановку надо сделать в том или ином случае.
Пример.
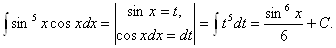
Этот пример можно было бы решить и так:
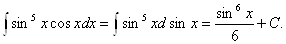
Такой метод интегрирования называется методом введения функции под знак дифференциала.
3. Пусть и(х), v(x) тАУ функции, которые имеют на некотором промежутке непрерывные производные. Тогда
d(uv) = udv + vdu
или
udv= d(uv) тАУvdu.
Интегрируя это равенство, получим
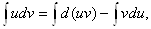
или, учитывая свойство 2 неопределённых интегралов,
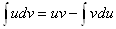 .
.
Эту формулу называют формулой интегрирования по частям.
Укажем некоторые интегралы, которые удобно вычислять методом интегрирования по частям:
1) в интегралах 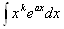
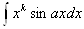
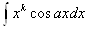 , где k тАУ натуральное число, за и следует брать хk, а за dv тАУ выражение, которое осталось;
, где k тАУ натуральное число, за и следует брать хk, а за dv тАУ выражение, которое осталось;
2) в интегралах 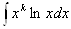
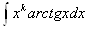
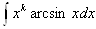
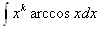 , следует обозначать dv= хkdx.
, следует обозначать dv= хkdx.
Неопределённый интеграл существует для произвольной непрерывной функцииf(x), то есть 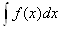 =F(x) +С. Но при этом не всегда первообразная F(x) является элементарной функцией. О таких интегралах говорят, что они тАЭне берутсятАЭ. Например, Ва
=F(x) +С. Но при этом не всегда первообразная F(x) является элементарной функцией. О таких интегралах говорят, что они тАЭне берутсятАЭ. Например, Ва
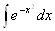 =F(x) +С,ВаВа где F(x) = х -
=F(x) +С,ВаВа где F(x) = х - 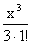 +
+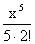 -
-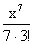 +.. .
+.. .
Не берутся такие интегралы:
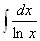 Ва- интегральный логарифм,
Ва- интегральный логарифм, 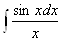 Ва- интегральный синус,
Ва- интегральный синус, 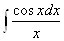 - интегральный косинус,
- интегральный косинус, 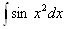 ,
, 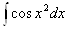 Ва- интегралы Френеля и другие.
Ва- интегралы Френеля и другие.
ВаВаВаВаВа В связи с этим важно выделить такие классы функций, интегралы от которых всегда выражаются через элементарные функции. Одним из таких классов функций, интегралы от которых Вавсегда тАЭберутсятАЭ, является класс рациональных функций.
Лекция 13.Ва Тема тАУЭлементарные дроби и их интегрирование.Интегрирование некоторых иррациональных и тригонометрических функций.
План.
1. Рациональные функции. Элементарные дроби и их интегрирование.
2. Разложение правильной рациональной дроби на элементарные дроби.
3. Интегрирование некоторых иррациональных и тригонометрических функций.
1.Рациональной функцией или рациональной дробью называют дробь
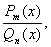
где Рт(х), Qn(x) тАУ многочлены степени т и п:
Qn(x) = 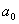 хп+
хп+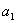 хп -1+..+
хп -1+..+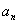 ,ВаВаВа Рт(х) =ВаВа
,ВаВаВа Рт(х) =ВаВа 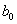 хт+
хт+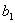 хт -1+..+
хт -1+..+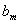 .
.
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателяВа т<п, и неправильной, если т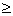 п.
п.
Неправильную дробь всегда можно записать в виде суммы многочлена и правильной дроби.
Поскольку многочлены интегрируются очень легко, то задача интегрирования рациональных функций сводится, таким образом, к интегрированию правильных дробей. Правильные дроби, в свою очередь раскладываются на элементарные дроби. Поэтому рассмотрим интегрирование элементарных дробей.
Различают четыре вида элементарных дробей:
РЖ.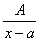 ,ВаВаВаВа РЖРЖ.
,ВаВаВаВа РЖРЖ. 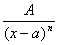 ,ВаВаВаВа РЖРЖРЖ.
,ВаВаВаВа РЖРЖРЖ. 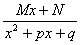 ,ВаВаВаВа РЖV.
,ВаВаВаВа РЖV. 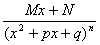 ,
,
где п=2,3,.., а трехчлен х2+рх+qне имеет действительных корней, то есть D=р2-4q<0.
Рассмотрим, как интегрируются эти дроби.
РЖ.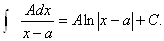
РЖРЖ. 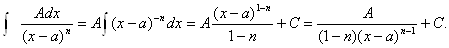
РЖРЖРЖ. Пример.
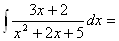
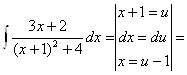
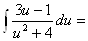
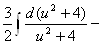

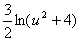 ---
---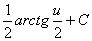 =
= 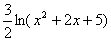 -
-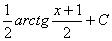 .
.
2. Как известно из алгебры, многочлен Qn(x) степени п может быть разложен на линейные и квадратичные множители
Qn(x) = 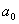 (х-х
(х-х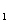 )k
)k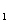 тАж(х-хr)k
тАж(х-хr)k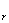 (x2+
(x2+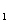 x+q
x+q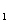 )l
)l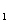 тАж(x2+p
тАж(x2+p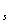 x+q
x+q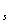 )l
)l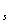 ,
,
гдеВа 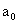 , х
, х ,
,  , q
, q Ва- действительные числа; k
Ва- действительные числа; k , I
, I Ва- натуральные числа; k
Ва- натуральные числа; k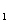 +тАж+ k
+тАж+ k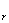 +2(I
+2(I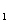 +тАж+ I
+тАж+ I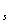 )=, р
)=, р 2- 4 q
2- 4 q <0.
<0.
ВаВаВаВаВа Рассмотрим правильную рациональную дробь
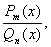
знаменатель которой уже разложен на линейные и квадратичные множители. Тогда эту дробь можно разложить на сумму элементарных дробей по таким правилам:
1) множителю (х-а)k соответствует сумма дробей вида
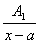 +
+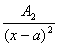 +тАж+
+тАж+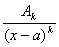 ;
;
2) множителю (x2+px+q)I соответствует сумма дробей вида
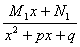 +
+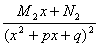 +тАж+
+тАж+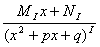 ,
,
где А ,М
,М ,N
,N - неопределённые коэффициенты.
- неопределённые коэффициенты.
Искать эти Ванеопределённые коэффициенты можно исходя из того, что равные многочлены имеют равные коэффициенты при одинаковых степенях х.
Пример. Вычислить интеграл
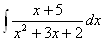 .
.
Решение.
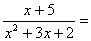
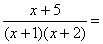
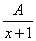 +
+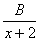 ,
,
х+5=А(х+2)+В(х+1),
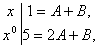 ВаВаВа А=4,ВаВа В=-3.
ВаВаВа А=4,ВаВа В=-3.
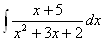 = 4
= 4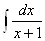 -3
-3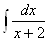 = 4ln
= 4ln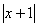 -3ln
-3ln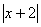 +C.
+C.
3. 1. Интегралы вида
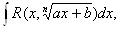
где R(х, у) тАУ рациональная функция относительно х и у, 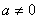 , сводятся к интегралам от рациональных функций с помощью подстановки
, сводятся к интегралам от рациональных функций с помощью подстановки
ax+=t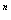 .
.
Ва2. Интегралы вида

где R тАУ рациональная функция, p , q
, q Ва- целые числа, сводятся к интегралам от рациональных функций с помощью подстановки
Ва- целые числа, сводятся к интегралам от рациональных функций с помощью подстановки
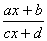 =t
=t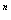 ,
,
где п тАУ общий знаменатель дробей 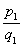 ,
,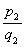 ,тАж .
,тАж .
3. Интегралы вида
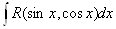 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(6.1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(6.1)
всегда сводятся к интегралам от рациональных функций с помощью, так называемой, универсальной тригонометрической подстановки
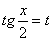 ,ВаВаВаВаВаВаВаВа
,ВаВаВаВаВаВаВаВа 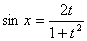 ,ВаВаВаВаВаВаВаВа
,ВаВаВаВаВаВаВаВа 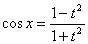 ,
,
х=2arctgt,ВаВаВаВаВаВа dx=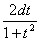 .
.
Замечание. Универсальная тригонометрическая подстановка всегда приводит к цели, но в силу своей универсальности она часто требует неоправданно громоздких вычислений. Поэтому во многих случаях удобнее пользоваться другими подстановками. Рассмотрим некоторые из них.
1) Если в интеграле (6.1) R(-sin x, cosx)= - R(sin x, cosx), то удобно делать подстановку cos x=t.
2) Если R(sin x,-cosx)= - R(sin x, cosx), то удобно делать подстановку sin x=t.
3) Если R(-sin x, -cosx)= R(sin x, cosx), то удобно делать подстановку
tg x=t,ВаВаВа 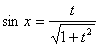 ,ВаВаВаВа
,ВаВаВаВа 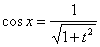 ,
,
х=arctgt,ВаВаВаВаВаВа dx=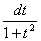 .
.
ВаВаВаВаВаВаВаВа 4. Рассмотрим более детально интегралы вида
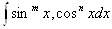 ,
,
где т, п тАУ целые числа.
1) Если т тАУ нечётное положительное число, то удобно делать подстановку cos x=t.
2) Если пВа тАУ нечётное положительное число, то удобно делать подстановку sin x=t.
3) Если оба показателя т и п тАУ чётные неотрицательные числа, то надо делать понижение степени синуса и косинуса по формулам
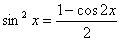 ,ВаВаВаВаВа
,ВаВаВаВаВа 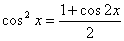 .
.
4) Для нахождения интегралов вида
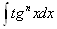 ,ВаВаВаВаВа
,ВаВаВаВаВа 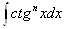
удобно пользоваться формулами
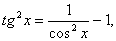
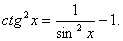
Ва5. В интегралах
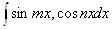 ,ВаВа
,ВаВа 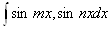 ,ВаВа
,ВаВа 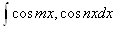 ,ВаВаВа
,ВаВаВа 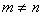
надо подынтегральную функцию записать в виде суммы функций с помощью формул
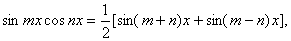
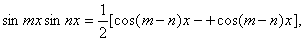
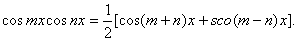
Лекция 14.Ва Тема тАУ Задача о площади криволинейной трапеции.Определённыйинтеграл его геометрический смысл и свойства.
Формула Ньютона-Лейбница.
План.
1. Задача о площади криволинейной трапеции. Определение и существование определённого интеграла.
2. Геометрический смысл определённого интеграла. Свойства определённого интеграла.
3.Ва Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
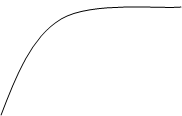 1. Криволинейной трапецией называется фигура, ограниченная линией у= f(x) и прямыми х=а, х=, у=0. Будем считать, что f(x)
1. Криволинейной трапецией называется фигура, ограниченная линией у= f(x) и прямыми х=а, х=, у=0. Будем считать, что f(x)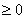 на [a;].
на [a;].





 уВаВаВаВаВаВаВаВаВаВаВаВаВаВа у= f(x)
уВаВаВаВаВаВаВаВаВаВаВаВаВаВа у= f(x)

0ВаВаВаВаВаВаВаВаВаВаВа а х ВаВаВа х
ВаВаВа х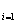
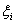 х
х x
x
ВаВаВаВаВа Разобьём отрезок [a;] произвольным образом на п частей точками а=х <x
<x <тАж< х
<тАж< х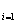 < х
< х <тАж<х
<тАж<х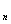 =.ВаВа
=.ВаВа
На каждом отрезке [х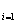 ; х
; х ] возьмём произвольную точкуВа
] возьмём произвольную точкуВа 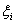 Ваивычислимзначение f(
Ваивычислимзначение f(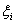 ). Тогда площадь S
). Тогда площадь S заштрихованного прямоугольника, будет равна
заштрихованного прямоугольника, будет равна
S = f(
= f(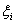 )
)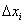 , ВаВагде
, ВаВагде 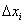 = х
= х - х
- х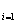 .
.
Площадь S всей трапеции приблизительно равна
S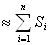
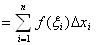 .
.
Пусть 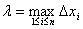 . Естественно считать, что
. Естественно считать, что
S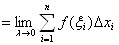 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6.2)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (6.2)
К пределам вида (6.2) приводят много других задач, поэтому возникает необходимость всестороннего изучения таких пределов независимо от конкретного содержания той или иной задачи.
Пусть функция у= f(x) определена на отрезке [a;]. Разобьём этот отрезок наВа п произвольных частей точками
а=х <x
<x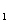 <тАж< х
<тАж< х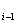 < х
< х <тАж<х
<тАж<х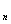 =.
=.
На каждом из созданных отрезков [х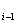 ; х
; х ] возьмём произвольную точкуВа
] возьмём произвольную точкуВа 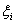 Ваи составим сумму
Ваи составим сумму
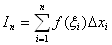 ,ВаВа где
,ВаВа где 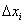 = х
= х - х
- х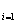 ,
,
которую будем называть интегральной суммой функции f(x).
Обозначим 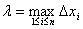 . Если существует конечный предел интегральной суммы
. Если существует конечный предел интегральной суммы 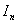 , при
, при 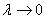 , который не зависит ни от способа разбиения отрезка [a;], ни от выбора точек
, который не зависит ни от способа разбиения отрезка [a;], ни от выбора точек
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Аксонометричнi проекцii