Чисельнi методи розвтАЩязування крайових задач для звичайних диференцiальних рiвнянь
Мiнiстерство освiти i науки Украiни
Сумський Державний Унiверситет
Кафедра РЖнформатики
Курсова робота
на тему:
ВлЧисельнi методи розвтАЩязування крайових задач для звичайних диференцiальних рiвняньВ»
ВлМетод скiнченних рiзницьВ»
Суми 2006
Змiст
Вступ
Постановка задачi
Метод скiнчених рiзниць
Дослiдження точностi
Збiжнiсть рiзницевоi схеми
Програмна реалiзацiя(представлена на мовi Delphi
Висновки
Лiтература
Вступ
На сьогоднiшнiй день iснуi багато чисельних методiв розвтАЩязування крайових задач для звичайних диференцiальних рiвнянь. Але всi вони подiляються на двi групи: наближенi методи чисельного розвтАЩязання i наближенi аналiтичнi методи.
Наближенi чисельнi методи:
1.Розв'язання лiнiйноi крайовоi задачi комбiнуванням двох задач Кошi:
Припустимо, що розв'язок задачi (11.4), (11.5) будемо шукати у виглядi
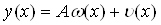 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.6)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.6)
де 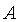 Ва- деяка константа,
Ва- деяка константа, 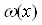 Ва- функцiя, що задовольняi однорiдне рiвняння
Ва- функцiя, що задовольняi однорiдне рiвняння
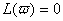 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.7)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.7)
а 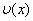 Ва- функцiя, яка задовольняi неоднорiдне рiвняння
Ва- функцiя, яка задовольняi неоднорiдне рiвняння
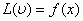 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.8)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.8)
Через те, що рiвняння (11.4) i лiнiйним, функцiя 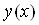 буде його розв'язком для будь-якого
буде його розв'язком для будь-якого 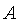 . Справдi,
. Справдi,
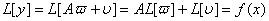
Якщо припустити, що розвтАЩязок (11.6) задовольняi першу граничну умову (11.5) для будь-якого 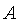 , то отримаiмо рiвняння
, то отримаiмо рiвняння
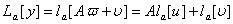
Ця гранична умова задовольняiться, якщо покласти
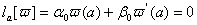 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.9)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.9)
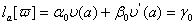 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.10)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.10)
Рiвнiсть (11.9) справедлива, коли прийняти, наприклад, що
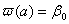 ,
, 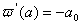 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.11)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.11)
Щоб задовольнити рiвнiсть (11.10), можна покласти
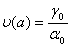 ,
, 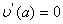 , якщо
, якщо 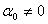 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.12)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.12)
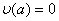 ,
, 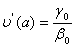 , якщо
, якщо 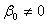 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.13)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.13)
Враховуiмо, що одночасно 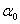 Ваi
Ваi 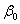 Вана нуль не перетворюються через умову (11.5).
Вана нуль не перетворюються через умову (11.5).
Таким чином, для розв'язання крайовоi задачi (11.4), (11.5) необхiдно знайти розв'язок задач
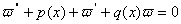 ,
, 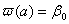 ,
, 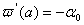 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.14)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.14)
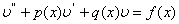 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.15)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.15)
з початковими умовами (11.12) чи (11 13). Для цього можна використати будь-який чисельний метод розв'язання задачi Кошi для рiвнянь другого порядку. Наближений розв'язок цих рiвнянь отримуiмо на вiдрiзку  , у результатi чого стають вiдомими значення
, у результатi чого стають вiдомими значення 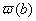 ,
,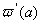 ,
,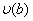 ,
,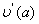 . Це дозволяi вибрати таку константу
. Це дозволяi вибрати таку константу 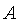 . щоб функцiя (11.6) задовольняла не тiльки рiвняння (11.12) i першу граничну умову, але i другу граничну умову (11.5). Маiмо
. щоб функцiя (11.6) задовольняла не тiльки рiвняння (11.12) i першу граничну умову, але i другу граничну умову (11.5). Маiмо
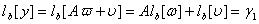 ,
,
звiдки
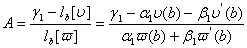 ,
,
якщо 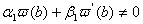 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.16)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.16)
Коли 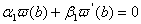 , то однорiдна крайова задача
, то однорiдна крайова задача
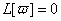 ,
, 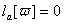 ,
, 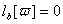
мас нетривiальний розв'язок 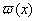 , який i ознакою виродженостi початковоi задачi (11.4), (11.5).
, який i ознакою виродженостi початковоi задачi (11.4), (11.5).
2. Метод прицiлювання:
Викладений вище метод редукцii крайовоi задачi до задачi Кошi маi певнi недолiки.
Вiн не дозволяi використовувати методи розв'язання задачi Кошi зi змiнним порядком i змiнним кроком. Розв'язки 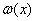 Ваi
Ваi 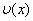 Ваповиннi обчислюватись на сiтцi з однаковим кроком, iнакше знайти iх комбiнацiю (11.6) буде неможливо.
Ваповиннi обчислюватись на сiтцi з однаковим кроком, iнакше знайти iх комбiнацiю (11.6) буде неможливо.
Використання методу, як правило, обмежуiться лише одновимiрною лiнiйною задачею. Причина полягаi в тому, що пiд час розв'язання системи рiвнянь потрiбно обчислювати не одне значення константи А (11.16), а матрицю А, що i далеко не простою задачею.
Метод не придатний для розв'язання нелiнiйних крайових задач.
Цi недолiки спричинилися до появи нових методiв. На практицi двоточкова крайова задача (лiнiйна чи нелiнiйна) звичайно розв'язуiться методом прицiлювання (стрiльби), назва якого запозичена iз теорii артилерiйськоi стрiльби. Вiдповiдно до цього методу розв'язок шуканого рiвняння другого порядку
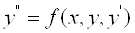
iз заданими граничними умовами
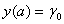 ,
, 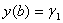 ,
, 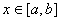
знаходять у такий спосiб: iтерацiйним розв'язанням задачi Кошi
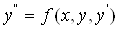 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(11.18)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(11.18)
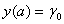 Ваi
Ваi 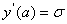
пiдбираiться значення першоi похiдноi 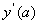 , для якоi виконуiться друга крайова умова
, для якоi виконуiться друга крайова умова 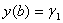 .
.
Спочатку вибираiться довiльне значення 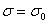 Ваi розв'язуiться задача Кошi (11.18). Значення
Ваi розв'язуiться задача Кошi (11.18). Значення 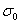 Вабажано вибирати так, щоб наближений розв'язок на кiнцi iнтервалу задовольняв умову
Вабажано вибирати так, щоб наближений розв'язок на кiнцi iнтервалу задовольняв умову 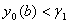 Ва(рис 1.). Потiм вибираiться
Ва(рис 1.). Потiм вибираiться 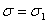 , i розв'язання задачi Кошi повторюiться. Тепер бажано вибрати його так, щоб виконувалась умова
, i розв'язання задачi Кошi повторюiться. Тепер бажано вибрати його так, щоб виконувалась умова 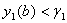 Ва(рис 1.).
Ва(рис 1.).
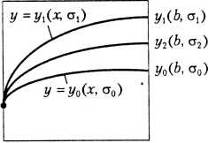
рис. 1. РЖлюстрацiя методу стрiльби.
Пiсля цього шляхом iнтерполяцii уточнюiться значення 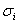 Вадля задач Кошi з початковими умовами:
Вадля задач Кошi з початковими умовами:
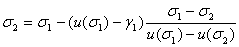 ,
,
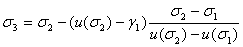
тАжтАж.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа тАжтАж.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа тАжтАж.
де 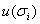 Ва- наближений розв'язок задачi Кошi в точцi
Ва- наближений розв'язок задачi Кошi в точцi 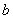 Вадля вибраного значення
Вадля вибраного значення 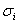 .
.
Метод прицiлювання i унiверсальним i використовуiться для розв'язання нелiнiйних диференцiальних рiвнянь 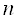 -ого порядку. Слiд зазначити, що довiльний вибiр початкового наближення
-ого порядку. Слiд зазначити, що довiльний вибiр початкового наближення 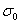 Ваможе привести до того, що задача (11.18) виявиться жорсткою навiть у випадку, коли задача (11.1), (11.2) i добре обумовленою.
Ваможе привести до того, що задача (11.18) виявиться жорсткою навiть у випадку, коли задача (11.1), (11.2) i добре обумовленою.
Наближенi аналiтичнi методи:
3.Метод колокацiй:
У методi колокацiй розв'язок крайовоi задачi (11.4), (11.5) шукаiться у виглядi функцii
 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.36)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.36)
де 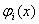 ,
, 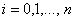 Ва- лiнiйно незалежнi, двiчi диференцiйованi базиснi функцii, визначенi на вiдрiзку
Ва- лiнiйно незалежнi, двiчi диференцiйованi базиснi функцii, визначенi на вiдрiзку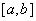 . Функцiя
. Функцiя 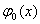 Ваповинна задовольняти заданi граничнi умови (11.5):
Ваповинна задовольняти заданi граничнi умови (11.5):
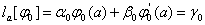
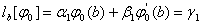 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.37,а)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.37,а)
а функцii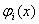 ,
, 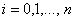 Ва- вiдповiднi однорiднi граничнi умови, тобто
Ва- вiдповiднi однорiднi граничнi умови, тобто
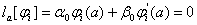 ,
,
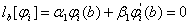 ,
,
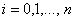 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.37,б)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.37,б)
Через лiнiйнiсть граничних умов функцiя 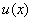 Вау (11.36) задовольняi граничним умовам (11.24) для будь-яких значень
Вау (11.36) задовольняi граничним умовам (11.24) для будь-яких значень 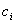 . Наприклад, у точцi
. Наприклад, у точцi 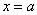 Вамаiмо
Вамаiмо
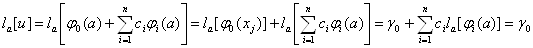 .
.
Аналогiчно для 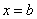 Ваотримаiмо
Ваотримаiмо
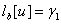
Суть методу колокацiй полягаi в тому, що для заданих 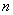 Ваточок на вiдрiзку
Ваточок на вiдрiзку 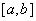 , названих вузлами колокацii, пiдбирають значення
, названих вузлами колокацii, пiдбирають значення 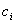 Ватак, щоб отримана при цьому функцiя
Ватак, щоб отримана при цьому функцiя 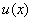 Ва(11.36) задовольняла рiвняння (11.4) у кожному з вузлiв колокацii:
Ва(11.36) задовольняла рiвняння (11.4) у кожному з вузлiв колокацii:
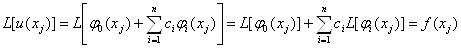 ,
,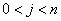 (11.38)
(11.38)
де
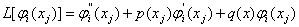 ,
, 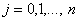 .
.
Покладемо
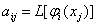 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.39)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.39)
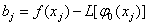
тодi (11.39) матиме стандартний вигляд системи лiнiйних алгебраiчних рiвнянь:
 ,
, 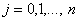 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.40)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.40)
вiдносно коефiцiiнтiв 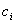 . Якщо розв'язати цю систему i пiдставити отриманi значення коефiцiiнтiв у вираз (11.36), отримаiмо наближений розв'язок
. Якщо розв'язати цю систему i пiдставити отриманi значення коефiцiiнтiв у вираз (11.36), отримаiмо наближений розв'язок 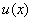 .
.
Точнiсть розв'язку крайовоi задачi методом колокацiй залежить вiд типу базисних функцiй 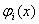 . У конкретних задачах вибiр цих функцiй слiд здiйснювати з урахуванням апрiорноi iнформацii про розв'язки задачi або на основi емпiричних даних. Нехай
. У конкретних задачах вибiр цих функцiй слiд здiйснювати з урахуванням апрiорноi iнформацii про розв'язки задачi або на основi емпiричних даних. Нехай 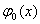 Ва- це лiнiйна функцiя
Ва- це лiнiйна функцiя
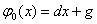 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.41)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.41)
параметри якоi визначимо таким чином, щоб вона задовольняла неоднорiднi граничнi умови (11.5), тобто з системи рiвнянь
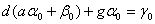 ,
,
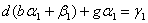 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.42)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.42)
Функцii 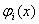 Ваможна задати у виглядi:
Ваможна задати у виглядi:
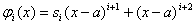 ,
, 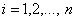 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.43)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.43)
Очевидно, що за будь-яких 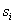 Вафункцiя (11.43) задовольняi умову (11.37, а). Значення
Вафункцiя (11.43) задовольняi умову (11.37, а). Значення 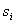 , за якого буде задовольнятися друга умова (11.37, б), таке:
, за якого буде задовольнятися друга умова (11.37, б), таке:
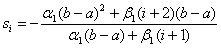 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.44)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.44)
Якщо в умовах (11.37, а, б) 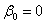 , то можливий iнший вибiр, а саме:
, то можливий iнший вибiр, а саме:
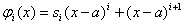 ,
,
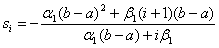 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.45)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.45)
4.Метод Гальоркiна
Як i в методi колокацiй, у методi Гальоркiна наближений розв'язок крайовоi задачi (11.4), (11.5) шукаiмо у виглядi
 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.48)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.48)
де 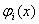 ,
, 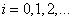 Ва- лiнiйно незалежнi, двiчi диференцiйованi базиснi функцii, визначенi на вiдрiзку
Ва- лiнiйно незалежнi, двiчi диференцiйованi базиснi функцii, визначенi на вiдрiзку 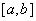 . Функцiя
. Функцiя 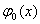 Ваповинна задовольняти заданi граничнi умови (11.37, а), а функцii
Ваповинна задовольняти заданi граничнi умови (11.37, а), а функцii 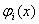 ,
, 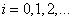 Ва- вiдповiднi однорiднi граничнi умови (11.37, 6).
Ва- вiдповiднi однорiднi граничнi умови (11.37, 6).
Необхiдно, щоб система базисних функцiй 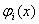 ,
, 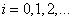 Вабула ортогональною на вiдрiзку
Вабула ортогональною на вiдрiзку 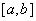 , тобто
, тобто
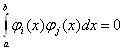 Вапри
Вапри 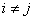 Ваi
Ваi 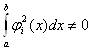 ,
,
i повною. Остання вимога означаi, що не повинно iснувати нiякоi iншоi вiдмiнноi вiд нуля функцii, яка ортогональна до всiх функцiй 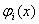 ,
, 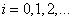 .
.
Використовуючи наближений розв'язок (11.48) знайдемо нев'язку:
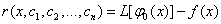 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.49)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.49)
Коефiцiiнти 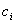 Вамають бути такими, щоб значення iнтеграла вiд квадрата нев'язки
Вамають бути такими, щоб значення iнтеграла вiд квадрата нев'язки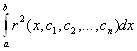
було найменшим.
Це досягаiться лише в тому випадку, коли нев'язка 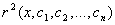 Ваортогональна до всiх базисних функцiй
Ваортогональна до всiх базисних функцiй 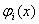 . Умову ортогональностi запишемо у виглядi:
. Умову ортогональностi запишемо у виглядi:
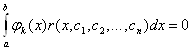 ,
, 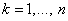
або
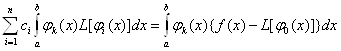 ,
, 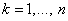 ВаВаВаВаВаВаВаВаВаВаВа (11.50)
ВаВаВаВаВаВаВаВаВаВаВа (11.50)
Таким чином, отримаiмо систему лiнiйних алгебраiчних рiвнянь для обчислення коефiцiiнтiв 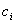
5.Метод найменших квадратiв
У методi найменших квадратiв наближений розв'язок крайовоi задачi (11.4) i (11.5) задасться у виглядi:
 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.54)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.54)
де 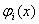 ,
, 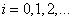 Ва- лiнiйно незалежнi, двiчi диференцiйованi базиснi функцii, визначенi на вiдрiзку
Ва- лiнiйно незалежнi, двiчi диференцiйованi базиснi функцii, визначенi на вiдрiзку 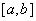 . Функцiя
. Функцiя 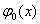 Ваповинна задовольняти заданi граничнi умови (11.37, а), а функцii
Ваповинна задовольняти заданi граничнi умови (11.37, а), а функцii 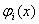 ,
, 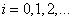 Ва- вiдповiднi однорiднi граничнi умови (11.38, б).
Ва- вiдповiднi однорiднi граничнi умови (11.38, б).
Пiдставимо наближений розв'язок (11.54) у рiвняння (11.4) i знайдемо нев'язку:
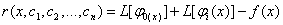 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.55)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.55)
абсолютна величина якоi для 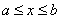 Ваповинна бути якомога меншою. Тому вимагатимемо, щоб виконувалася умова
Ваповинна бути якомога меншою. Тому вимагатимемо, щоб виконувалася умова
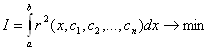 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.56)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.56)
Значення iнтегралу будуть мiнiмальними за умов:
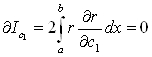 ,
,
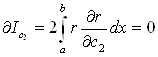 ,
,
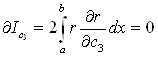 ,
,
тАжВаВаВаВаВа тАжВаВаВаВаВа тАжВаВаВаВаВа тАж
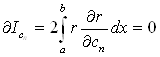 .
.
На основi цих умов формуiться система лiнiйних рiвнянь для обчислення коефiцiiнтiв 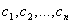 .
.
6.Метод скiнченних елементiв
Метод Гальоркiна накладаi певнi обмеження на вибiр системи базисних функцiй, якi залежать вiд граничних умов крайовоi задачi. Це обмеження значно ускладнюi реалiзацiю методу, особливо пiд час розв'язання задач математичноi фiзики. Це обмеження можна подолати, якщо для апроксимацii розв'язку використовувати систему простих базисних функцiй, якi залежать вiд координат вузлiв на вiдрiзку 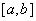 . У цьому випадку розв'язання крайовоi задачi зводиться до формування i розв'язання системи лiнiйних алгебраiчних рiвнянь, тому метод отримав назву методу скiнченних елементiв. Його часто використовують для розв'язання дво- та тривимiрних диференцiальних рiвнянь iз частинними похiдними.
. У цьому випадку розв'язання крайовоi задачi зводиться до формування i розв'язання системи лiнiйних алгебраiчних рiвнянь, тому метод отримав назву методу скiнченних елементiв. Його часто використовують для розв'язання дво- та тривимiрних диференцiальних рiвнянь iз частинними похiдними.
Шукатимемо наближений розв'язок задачi
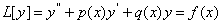 ,
, 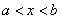 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.59)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.59)
як лiнiйну комбiнацiю простих однотипних функцiй
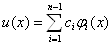 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.60)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.60)
що мають вигляд
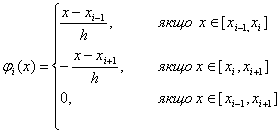 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.61)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.61)
i, як правило, називаються фiнiтними. Графiк однiii з таких функцiй наведено на рис. 2, де видно, що функцiя не дорiвнюi нулю тiльки на iнтервалi 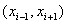 . Щодо множини фiнiтних функцiй, якi задаються на вiдрiзку
. Щодо множини фiнiтних функцiй, якi задаються на вiдрiзку 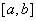 Вавiдомо, що вони лiнiйно незалежнi (бiльш того, ортогональнi в спецiальнiй енергетичнiй нормi) i утворюють повну систему в просторi
Вавiдомо, що вони лiнiйно незалежнi (бiльш того, ортогональнi в спецiальнiй енергетичнiй нормi) i утворюють повну систему в просторi 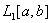 .Це даi пiдставу використати iх як базиснi функцii в методi Гальоркiна.
.Це даi пiдставу використати iх як базиснi функцii в методi Гальоркiна.
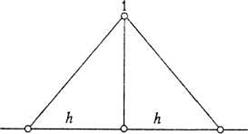
рис. 2. Графiк фiнiтноi функцii.
Запишемо умову ортогональностi (11.50):
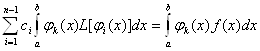 ,
, 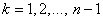 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.62)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.62)
i отримаiмо систему лiнiйних алгебраiчних рiвнянь для знаходження невiдомих 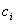 .Правi частини цих рiвнянь позначимо через
.Правi частини цих рiвнянь позначимо через 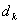 Ваi отримаiмо для iх обчислення вираз
Ваi отримаiмо для iх обчислення вираз
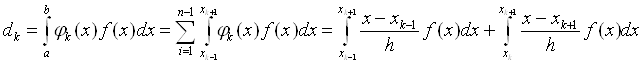 (11.63)
(11.63)
Коефiцiiнти системи рiвнянь (11.62) позначимо через
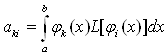
Знайдемо вирази для коефiцiiнтiв системи рiвнянь 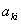 Ваз невiдомими
Ваз невiдомими 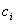 . Пiдставляючи в останнiй вираз
. Пiдставляючи в останнiй вираз 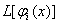 , отримаiмо
, отримаiмо
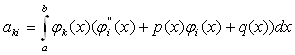
Перший з iнтегралiв у цьому виразi обчислимо по частинах:
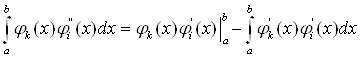
Оскiльки за граничних умов (11.60) використовуються 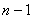 , базисних функцiй вiд
, базисних функцiй вiд 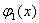 Вадо
Вадо 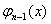 Ваi всi вони в точках
Ваi всi вони в точках 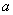 Ваi
Ваi 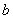 Вадорiвнюють 0, то
Вадорiвнюють 0, то
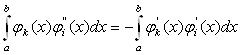
Тодi вираз для обчислення набуваi вигляду:
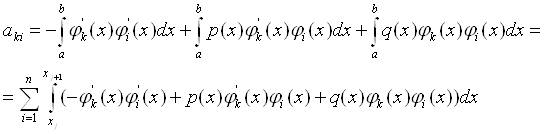 (11.64)
(11.64)
Для обчислення 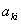 Ватреба знайти значення похiдних вiд фiнiтних функцiй. РЖз цiiю метою диференцiюiмо (11.61) i отримуiмо:
Ватреба знайти значення похiдних вiд фiнiтних функцiй. РЖз цiiю метою диференцiюiмо (11.61) i отримуiмо:
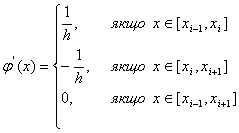 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.65)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.65)
Функцiя вiдмiнна вiд нуля тiльки на iнтервалi 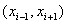 . Крiм того, на одному i тому ж iнтервалi ненульовими i двi базиснi функцii i iх похiднi з сусiднiми iндексами (рис. 3), тобто на iнтервалi
. Крiм того, на одному i тому ж iнтервалi ненульовими i двi базиснi функцii i iх похiднi з сусiднiми iндексами (рис. 3), тобто на iнтервалi 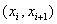 Вавiдмiннi вiд нуля
Вавiдмiннi вiд нуля 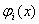 ,
, 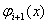 ,
, 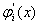 ,
, 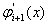 Ваi т. д.
Ваi т. д.

рис. 3. Система фiнiтних функцiй.
У виразi для 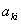 Ва(11.64) добутки
Ва(11.64) добутки 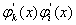 ,
, 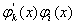 ,
, 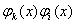 Ваможна вважати вiдмiнними вiд нуля тому, що на елементарному iнтервалi не дорiвнюють нулю фiнiтнi функцii та iх похiднi, якi мають сусiднi iндекси у випадках, коли
Ваможна вважати вiдмiнними вiд нуля тому, що на елементарному iнтервалi не дорiвнюють нулю фiнiтнi функцii та iх похiднi, якi мають сусiднi iндекси у випадках, коли 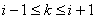 . А це означаi, що
. А це означаi, що
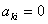 Вадля
Вадля 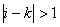 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.66)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.66)
тобто матриця системи 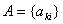 Ва(11.62) i тридiагональною матрицею. ii ненульовi елементи обчислюються таким чином. Формули для дiагональних елементiв отримаiмо, приймаючи
Ва(11.62) i тридiагональною матрицею. ii ненульовi елементи обчислюються таким чином. Формули для дiагональних елементiв отримаiмо, приймаючи 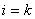 Вау виразi (11.64):
Вау виразi (11.64):
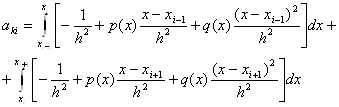 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.67)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.67)
Для 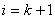 , отримаiмо формули для елементiв правоi бiчноi дiагоналi матрицi
, отримаiмо формули для елементiв правоi бiчноi дiагоналi матрицi 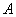 :
:
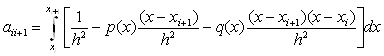 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.68)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.68)
а для 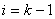 Ва- лiвоi;
Ва- лiвоi;
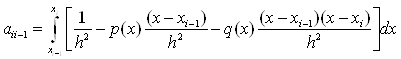
Три останнi вирази визначають систему алгебраiчних рiвнянь (11.62) для невiдомих коефiцiiнтiв 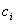 .
.
Розглянемо розвтАЩязання задачi (11.59) у випадку неоднорiдних граничних умов
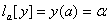 ,ВаВаВаВаВа
,ВаВаВаВаВа 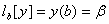 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.70)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.70)
i зведемо ii до розв'язання задачi з однорiдними граничними умовами. Для цього введемо замiну:
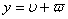 , де
, де 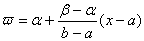 .
.
Двiчi диференцiюючи цю функцiю i пiдставляючи вирази для похiдних у рiвняння (11.59), отримаiмо крайову задачу з однорiдними граничними умовами:
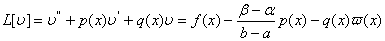 ,
,
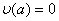 ,
, 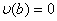 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.71)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.71)
Постановка задачi
Щоб знайти iдиний розв'язок звичайного диференцiального рiвняння, необхiдно задати деякi допомiжнi умови, що використовуються для обчислення iнтегрування. Для рiвняння n-ого порядку потрiбно п таких умов. Якщо цi умови задаються для одного значення незалежноi змiнноi (зокрема, для одного кiнця iнтервалу, на якому необхiдно знайти розв'язок), то говорять про початковi умови для задачi Кошi. Якщо ж додатковi умови задаються для значень незалежноi змiнноi на рiзних кiнцях iнтервалу, то мають на увазi крайову задачу i граничнi умови для неi.
Двоточкова крайова задача для рiвняння другого порядку маi такий вигляд:
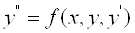
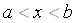 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.1)
iз граничними умовами
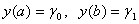 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.2)
Перш нiж застосовувати будь-який чисельний метод, варто перевiрити умови, що гарантують iснування розв'язку цiii задачi. Наведена нижче теорема визначаi загальнi умови, що забезпечують iснування й одиничнiсть розв'язку.
Теорема. Припустимо, що 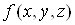 Ванеперервна в областi
Ванеперервна в областi
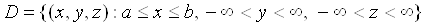
РЖ що
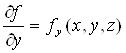 Ваi
Ваi 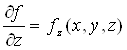
Теж неперервнi на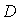 . Якщо iснуi постiйна
. Якщо iснуi постiйна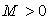 , для якоi виконуються умови
, для якоi виконуються умови
 для всiх
для всiх 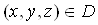
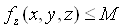 Вадля всiх
Вадля всiх 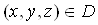 ВаВаВаВаВаВаВа (11.3)
ВаВаВаВаВаВаВа (11.3)
то крайова задача (11.1) (11.2) маi iдиний розв'язок 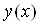 Вадля
Вадля 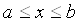 .
.
Найчастiше зустрiчаються i найкраще вивченi двоточковi лiнiйнi крайовi задачi виду
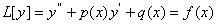 ,
, 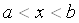 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.4)
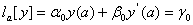 ,
, 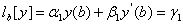 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.5)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.5)
де
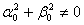 ,
, 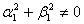
Умови, якi повиннi задовольняти функцii 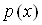 ,
, 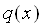 Ваi
Ваi 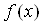 , для того щоб задача (11.4), (11.5) мала iдиний розв'язок, випливають iз теореми як наслiдок.
, для того щоб задача (11.4), (11.5) мала iдиний розв'язок, випливають iз теореми як наслiдок.
Наслiдок. Якщо 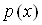 Ваi
Ваi 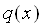 Ванеперервнi на
Ванеперервнi на 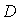 Ваi
Ваi 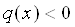 , то задача (11.4), (11.5) маi iдиний розв'язок на
, то задача (11.4), (11.5) маi iдиний розв'язок на 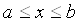 .
.
Граничнi умови (11.5) визначають третю крайову задачу для рiвняння (11.4). Якщо припустити, що 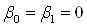 , то умови (11.5) визначають першу крайову задачу, а коли
, то умови (11.5) визначають першу крайову задачу, а коли 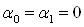 Ва- другу.
Ва- другу.
Точне (аналiтичне) розв'язання крайових задач - бiльш складна процедура, нiж знаходження розв'язку задачi Кошi. Це спричинило появу великоi кiлькостi наближених методiв. Цi методи можна роздiлити на двi групи: наближено-аналiтичнi методи, що дають наближений розв'язок крайовоi задачi на вiдрiзку  Вау виглядi конкретноi аналiтичноi функцii, i чисельнi методи, що визначають розвозок у виглядi табличноi функцii, заданоi на сiтцi вiдрiзка
Вау виглядi конкретноi аналiтичноi функцii, i чисельнi методи, що визначають розвозок у виглядi табличноi функцii, заданоi на сiтцi вiдрiзка  .
.
Метод скiнченних рiзниць
РЖдея методу скiнченних рiзниць полягаi в тому, що похiднi в диференцiальному рiвняннi (11.4) i граничних умовах (11.5) замiняються iх скiнченними рiзницями. Для цього спочатку введемо на вiдрiзку 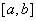 Васiтку з кроком
Васiтку з кроком 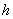 :
:
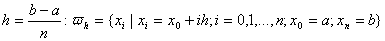 .
.
Позначимо через 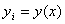 точний розв'язок задачi (11.1) у i-му вузлi сiтки, а через
точний розв'язок задачi (11.1) у i-му вузлi сiтки, а через 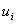 Ва- наближений розв'язок у цiй точцi. Замiняючи в кожному внутрiшньому вузлi сiтки похiднi рiзницями, отримаiмо рiзницевi рiвняння:
Ва- наближений розв'язок у цiй точцi. Замiняючи в кожному внутрiшньому вузлi сiтки похiднi рiзницями, отримаiмо рiзницевi рiвняння:
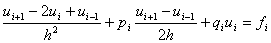 ,
, 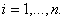
Симетричнi рiзницевi апроксимацii похiдних першого i другого порядкiв мають похибку другого порядку вiдносно 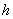 , тобто
, тобто 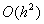 . Це легко довести на основi розкладання в ряд Тейлора точного розв'язку рiвняння. Дiйсно, для вузлiв
. Це легко довести на основi розкладання в ряд Тейлора точного розв'язку рiвняння. Дiйсно, для вузлiв 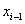 та
та 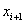 Вамаiмо
Вамаiмо
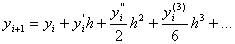
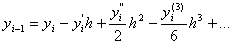
з рiзницi яких отримуiмо шуканий результат:
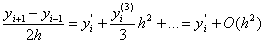 ,
,
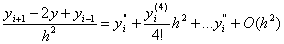 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВа (11.21)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВа (11.21)
Знайдемо невтАЩязку рiзницевого рiвняння
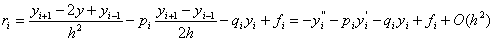 .
.
Оскiльки 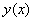 Ваi точним розв'язком рiвняння (11.4),
Ваi точним розв'язком рiвняння (11.4),
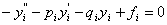 Вата
Вата 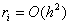 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.22)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.22)
Тому рiзницеве рiвняння (11.21) апроксимуi вихiдне диференцiальне рiвняння
(11.4) також iз другим порядком вiдносно 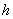 .
.
Тепер апроксимуiмо граничнi умови скiнченними рiзницями:
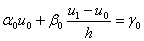 ,
, 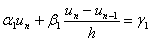 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.23)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.23)
Знайдемо похибку апроксимацii граничних умов. НевтАЩязки граничних умов (11.23) мають вигляд:
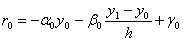 ,
, 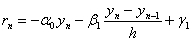 .
.
Асиметрична апроксимацiя першоi похiдноi на вiдмiну вiд симетричноi маi глобальну похибку першого порядку вiдносно 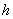 , тобто
, тобто 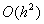 . Це безпосередньо випливаi з розкладання в ряд Тейлора
. Це безпосередньо випливаi з розкладання в ряд Тейлора
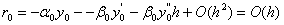 ,
,
iз якого отримуiмо
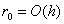 ,
, 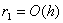
Отже, граничнi умови (11.23) апроксимуються з першим порядком за к. Порядок iх апроксимацii можна пiдвищити до другого, наприклад, використовуючи спiввiдношення

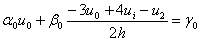 ,
,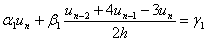 ВаВаВаВаВаВаВаВаВаВа (11.24)
ВаВаВаВаВаВаВаВаВаВа (11.24)
похибка апроксимацii яких також пропорцiйна 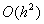 , як i для випадку симетричноi апроксимацii похiдних. Це випливаi iз порiвняння двох рядiв Тейлора:
, як i для випадку симетричноi апроксимацii похiдних. Це випливаi iз порiвняння двох рядiв Тейлора:
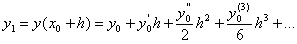
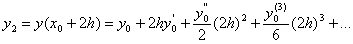
Якщо перший вираз помножити на 4 i вiдняти його вiд другого, отримаiмо:
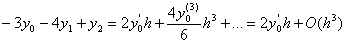 .
.
Пiсля його пiдстановки у формулу (11.24) знаходимо нев'язку у виглядi:
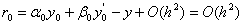
тобто крайова умова апроксимуiться з другим порядком вiдносно 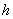 .
.
У такий же спосiб доводиться, що i друга гранична умова (11.23) апроксимуiться з другим порядком вiдносно 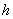 .
.
Розглянемо ще одну можливiсть апроксимацii крайових умов типу (11.5) на прикладi умови
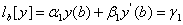 .
.
Для цього за межами iнтервалу 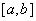 Вавводиться додаткова точка
Вавводиться додаткова точка 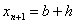 , за допомогою якоi обчислюiться перша похiдна за симетричною формулою апроксимацii:
, за допомогою якоi обчислюiться перша похiдна за симетричною формулою апроксимацii:
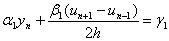 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.25)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.25)
Точку 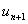 Ваможна виключити, скориставшись спiввiдношенням (11.25) i рiзницевою апроксимацiiю диференцiального рiвняння (11.4) в кiнцевiй точцi iнтервалу
Ваможна виключити, скориставшись спiввiдношенням (11.25) i рiзницевою апроксимацiiю диференцiального рiвняння (11.4) в кiнцевiй точцi iнтервалу 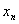 .
.
Отримуiмо рiвняння для граничноi умови в точцi 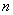 Ваiз порядком
Ваiз порядком 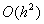 , яким можна замiнити останнi рiвняння в системi алгебраiчних рiвнянь, одержанiй у разi кусочно-рiзницевоi апроксимацii похiдних у рiвняннi (11.4).
, яким можна замiнити останнi рiвняння в системi алгебраiчних рiвнянь, одержанiй у разi кусочно-рiзницевоi апроксимацii похiдних у рiвняннi (11.4).
Те ж саме можна зробити з першою умовою (11.5) i першим апроксимуючим рiвнянням для 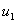 . Варто пiдкреслити, що врахування граничних умов рiзних типiв впливаi тiльки на перше й останнi рiвняння цiii системи.
. Варто пiдкреслити, що врахування граничних умов рiзних типiв впливаi тiльки на перше й останнi рiвняння цiii системи.
Зведемо подiбнi члени в рiвняннi (11.21) i отримаiмо стандартне триточкове рiзницеве рiвняння:
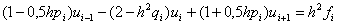 ,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.27)
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.27)
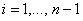 .
.
Включивши до системи рiвнянь (11.25) рiзницеве рiвняння (11.23) чи (11.24), отримаiмо систему рiвнянь, що мiстить 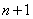 Варiвняння з
Варiвняння з 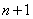 Ваневiдомими
Ваневiдомими 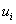 .
.
Порiвняiмо цi два варiанти апроксимацii крайовоi задачi. У першому з них система лiнiйних алгебраiчних рiвнянь, утворена рiвняннями (11.21) i (11.23), маi тридiагональну матрицю коефiцiiнтiв, i ii можна розв'язати методом прогону. Щоб застосувати метод прогону в другому випадку, слiд створити вiдповiдну тридiагональну матрицю. Для цього потрiбно з першого рiвняння (11.27) для 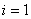
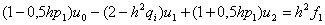
Маiмо рiвняння з двома невiдомими - 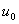 Ваi
Ваi 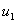 . Замiнимо ним перше рiвняння (11.24). Виконаiмо такi ж перетворення з другим (11.24) i останнiм рiвнянням (11.27) для
. Замiнимо ним перше рiвняння (11.24). Виконаiмо такi ж перетворення з другим (11.24) i останнiм рiвнянням (11.27) для 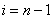 :
:
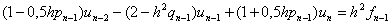
Виключивши з них 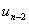 , знаходимо:
, знаходимо:
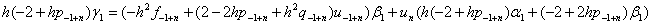
Це рiвняння мiстить двi невiдомi - 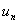 Ваi
Ваi 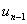 . Замiнимо ним друге рiвняння (11.27). Два останнi рiвняння разом iз (11.27) утворюють систему рiвнянь iз тридiагональною матрицею, що апроксимуi вихiдну крайову задачу (11.4), (11.5) з порядком
. Замiнимо ним друге рiвняння (11.27). Два останнi рiвняння разом iз (11.27) утворюють систему рiвнянь iз тридiагональною матрицею, що апроксимуi вихiдну крайову задачу (11.4), (11.5) з порядком 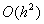 . Цю систему також можна розв'язати методом прогону. Метод прогону i стiйким, якщо матриця коефiцiiнтiв дiагонально домiнантна. Забезпечити дiагональну домiнантнiсть можна обранням кроку
. Цю систему також можна розв'язати методом прогону. Метод прогону i стiйким, якщо матриця коефiцiiнтiв дiагонально домiнантна. Забезпечити дiагональну домiнантнiсть можна обранням кроку 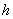 . Для цього необхiдно, щоб для системи рiвнянь (11.27) виконувались умови:
. Для цього необхiдно, щоб для системи рiвнянь (11.27) виконувались умови:
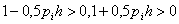 Ваi
Ваi 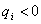 ,
, 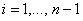 .
.
Пiдсилюючи останнi нерiвностi, маiмо такi обмеження на величину кроку:
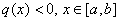 Ваi
Ваi 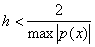 ,
, 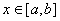 .ВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.28)
.ВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.28)
Щоб задовольнялись умови (11.23), мають виконуватись нерiвностi
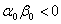 Ваi
Ваi 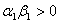 .ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.29)
.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (11.29)
Наявнiсть обмежень (11.28) i (11.29) свiдчить про умовну стiйкiсть розглянутого методу апроксимацii.
Дослiдження точностi
Дослiдження точностi отриманих виразiв при чисельних розрахунках зручно робити за допомогою апостерiорноi оцiнки, по швидкостi спадання членiв вiдповiдного ряду Тейлора. Якщо крок сiтки досить малий, то похибка близька до першого вiдкинутого члена.
У такий спосiб порядок точностi результату стосовно кроку сiтки дорiвнюi числу залишених членiв ряду, чи iншими словами, вiн дорiвнюi числу вузлiв iнтерполяцii мiнус порядок похiдноi. тому мiнiмальне число вузлiв необхiдне для обчислення m-оi похiдноi, дорiвнюi m+1, воно забезпечуi перший порядок точностi.
Цi висновки вiдповiдають принципу: при почленному диференцiюваннi ряду швидкiсть його збiжностi зменшуiться.
Якщо врахувати погiршення збiжностi ряду при диференцiюваннi, то можна зробити висновок: навiть якщо функцiя задана добре складеною таблицею на досить докладнiй сiтцi, то практично чисельним диференцiюванням можна визначити першу i другу похiднi, а третю i четверту тАУ лише з великою похибкою. Похiднi бiльш високого порядку рiдко вдаiться обчислити з задовiльною точнiстю.
Одним з найбiльш простих i досить ефективних методiв оцiнки похибки й уточнення отриманих результатiв i правило Рунге. Для оцiнки похибки за правилом Рунге порiвнюють наближенi розвтАЩязки, отриманi при рiзних кроках сiтки. При цьому використовуiться наступне припущення: глобальна похибка методу порядку у точцi хiподаiться у виглядi

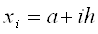 .
.
За формулою Рунге
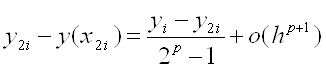
Таким чином, iз точнiстю до 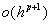 (величина бiльш високого порядку малостi) при h→0 похибка методу маi вигляд:
(величина бiльш високого порядку малостi) при h→0 похибка методу маi вигляд:
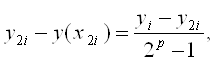
де yiтАУ наближене значення, отримане в точцi 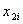 з кроком h; y2iтАУ iз кроком h/2; - порядок методу; y(x2i) - точний розвтАЩязок задачi.
з кроком h; y2iтАУ iз кроком h/2; - порядок методу; y(x2i) - точний розвтАЩязок задачi.
Формула Рунге:
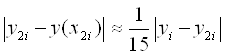 .
.
Збiжнiсть рiзницевоi схеми
Постановка задачi
Унiверсальним методом наближеного розвтАЩязання, i метод скiнченних рiзниць. Як задачi представленi у виглядi систем нелiнiйних рiвнянь у часткових, якi розглядаються у областi 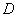
РозвтАЩязок задачi в 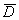 Вамаi додатковi умови:
Вамаi додатковi умови:
1) умови при 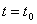 Ваназивають початковими умовами;
Ваназивають початковими умовами;
2) умови на границi 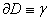 Ваобластi
Ваобластi 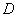 тАФ крайовими або граничними умовами.
тАФ крайовими або граничними умовами.
Задача з початковими умовами тАУ називаiться задачею Кошi.
Нехай 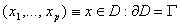 . Тодi для функцii
. Тодi для функцii 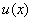 Вамаiмо задачу:
Вамаiмо задачу:
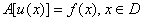 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
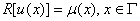 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
де 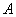 и
и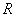 - диференцiальнi оператори задачi i крайових умов. Припустимо ,що вiдповiдно задачi (1-2) поставленi коректно, тобто оператори А и R; область D и ii границi Г такi, що при виборi вiдповiдних класiв функцiй i правих частин у рiвняннях (1) и (2) розвтАЩязок iснуi, i залежить вiд початкових даних.
- диференцiальнi оператори задачi i крайових умов. Припустимо ,що вiдповiдно задачi (1-2) поставленi коректно, тобто оператори А и R; область D и ii границi Г такi, що при виборi вiдповiдних класiв функцiй i правих частин у рiвняннях (1) и (2) розвтАЩязок iснуi, i залежить вiд початкових даних.
Рiзницева схема
Введемо у областi 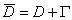 Васiтку
Васiтку 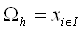 , яка складаiться з множини внутрiшнiх вузлiв
, яка складаiться з множини внутрiшнiх вузлiв 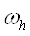 Ваi множини граничних вузлiв
Ваi множини граничних вузлiв  :
:
Далi розглянемо сiтковi функцii 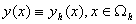 Ваi з iх допомогою побудуiмо наближений розвтАЩязок задачi (1-2). Для цього вiдносно
Ваi з iх допомогою побудуiмо наближений розвтАЩязок задачi (1-2). Для цього вiдносно 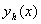 Васформулюiмо "рiзницеву задачу", замiняючи оператори задачi
Васформулюiмо "рiзницеву задачу", замiняючи оператори задачi 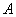 Ваi
Ваi 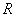 Ваi iх сiтковим аналогами
Ваi iх сiтковим аналогами 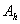 и
и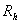 . Тодi на сiтковому шаблонi
. Тодi на сiтковому шаблонi 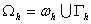 Вамаiмо
Вамаiмо
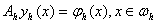 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
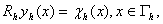 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
Задачу (3)-(4) назвемо рiзницевою схемою для задачi (1)-(2). Звичайно це алгебраiчна система рiвнянь вiдносно ![]()
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Аксонометричнi проекцii