Теорема Дирихле

Содержание

Введение. 2

1. Характеры. 3

1.1 Определение характера. Основные свойства характеров. 3

1.2 Суммы характеров. Соотношение ортогональности. 6

1.3 Характеры Дирихле. 8

2. L-функция Дирихле. 13

3. Доказательство теоремы Дирихле. 29

Введение

Простые числа расположены в натуральном ряде весьма неравномерно.

Целью данной работы является доказательство следующей теоремы о простых числах в арифметической прогрессии.

Теорема Дирихле. Если разность и первый член арифметической прогрессии есть взаимно простые натуральные числа, то она содержит бесконечное множество простых чисел.

Пусть

mn+ l, =1,2, тАж,

прогрессия, удовлетворяющая условию теоремы.

Условие (m, l)=1, наложенные на числа m и e в формулировке теоремы, естественно, поскольку в случае, когда d=(m, l)>1, все члены прогрессии делятся на d и поэтому не являются простыми числами.

Сформулированная теория была впервые высказана Л. Эйлером в 1783 г. В 1798 г. А. Лежандр опубликовал доказательство для четных m, использовавшее, как выяснилось позднее, одну ошибочную лемму.

Полностью доказал теорему в 1837тАУ1839 гг. Петер Густав Лежен-Дирихле (1805тАУ1859), немецкий математик, автор трудов по аналитической теории чисел, теории функций, математической физике.

В 1837 г. вышли две работы Дирихле, посвященные теореме о простых числах в арифметической прогрессии. Они содержали формулировку теоремы в общем виде, однако доказательство приводилось только для случая, когда разность прогрессии есть простое число. В конце второй работы содержится построение характеров для произвольного модуля и некоторые утверждения о том, как можно доказать утверждение L(1,χ)¹0 для неглавных характеров x в одном случае. В 1839 г. Дилихле опубликовал полное доказательство теоремы о простых числах в арифметической прогрессии. С тех пор она носит его имя.

1. Характеры

1.1 Определение характера. Основные свойства характеров

Характером (от греческого хараæτήp-признак, особенность) χ конечной абелевой группы G называется не равная тождественно нулю комплекснозначная функция, определенная на этой группе и обладающая тем свойством, что если, АÎGи BÎG

χ (АВ)= χ (А) χ(В).

Обозначим через Е единичные элементы в группе G и через А^-1 обратный элемент для АÎG

Характеры группы G обладают следующими свойствами:

1. Если Е-единица группы, то для каждого характера χ

χ (Е)=1 ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.1)

Доказательство. Пусть для каждого элемента АÎG справедливо неравенство

c₁(А)=c(АЕ)= c(А) χ (Е)

Из этого равенства получим, что c (Е)¹0. Теперь из равенства

c (Е)= c (ЕЕ)= c (Е) c (Е)=1

следует равенство (1.1)

2. c (А) ¹0 для каждого АÎG

Действительно, если бы χ (А) =0 для некоторого АÎG, то

c (А) χ (А^-1)= c (АА^-1)= χ (Е)=0,

а это противоречит свойству 1.

3. Если группа G имеет порядок h, то А^h=Е для каждого элемента АÎG Следовательно,

1= χ (Е)= χ (А^h)= χ (А)^h,

то есть χ (А) есть некоторый корень степени h из единицы.

Характер χ_1, обладающий свойством χ₁(А)=1 для каждого элемента АÎG, называется главным характером группы G. Остальные характеры называются неглавными.

Лемма 1. Пусть Н подгруппа конечной абелевой группы G, причем G/H тАУ циклическая порядка , тогда для каждого характера χ_HтАУ подгруппы Н существует ровно характеров.

Доказательство. Рассмотрим группу G=g^kH, причем gⁿH=H, gⁿÎH и gⁿ=h₁=1.

Для каждого элемента XÎG существует и притом единственное к=к_х и h_х=h такое, что если 0£ к_х k^х h_х=g^kh. Возьмем еще один элемент группы G, Y= g^mh_y, где 0£ m

ХY= g^к+mhh_y.

Определим характер χ (X).

χ (X)= χ (g^к h)= χ (g^к) χ (n)= χ ^к (g) χ_H (h).

В данном выражении неизвестным является χ (g).

χⁿ(g)= χ (gⁿ)= χ (h₁)= χ_H(h₁) тАУ данное число.

χ (g)= тАУ корней из 1,

то есть ξ_СШⁿ=χⁿ(g)= χ_H(h₁), получаем x^k(g)= ξ_СШⁿ. Следовательно, x(g)= ξ₁, тАж, ξ_n

Из полученных равенств получаем:

χ (X)= χ^k(g) χ_H(h_x)= ξ_j^kxχ_H (h_x)

χ (Y)= χ^m(g) χ_H(h_y)= ξ_j^kyχ_H (h_y)

Определим умножение характеров

χ (X) χ (Y)= ξ_j^kyχ_H (h_y) ξ_j^k-xχ_H (h_x)= ξ_j^kx+kyχ_H (h_x) χ_H (h_y)= _j^k+mχ_H (hh_y)

Для того чтобы определение выполнялось, необходимо рассмотреть степень g^kx+kx. Возможны два случая:

1) Если 0£ к_х + k_y

к_х + k_y= k_xy,; h_xh_y= h_xy.

В этом случае определение выполняется.

2) Если n£ к_х + k_y<2n-1, то получим

к_х + k_y = n + k_xy..

Тогда

XY= g ^kx+ky h_xh_y=g^hg^kx+ky-n h_x h_y=g^kx+ky-nh₁h_xh_y

В свою очередь 0£ к_х + k_y тАУ n£n-1 Þ k_x+k_y тАУ n=k_xy, h₁h_xh_y= h_xy.

χ (XY) = ξ_j^kх+kу χ_н (h_xу) = ξ_j^{kх + kу тАУ n}χ_н (h₁) χ_н(h_x) χ_н (h_y) = ξ_j^кх ξ_j ^ку ξ_j^{тАУ n} χ_н (h₁) χ_н(h_x) χ_н (h_y) = ξ_j ^кх χ_н (h_1х) В· ξ_j ^ку χ_н(h_y) = χ (X) χ(Y).

Лемма доказана.

5. Характеры конечной мультипликативной абелевой группы G образуют конечную мультипликативную абелевую группу Ĝ.

Под произведением двух характеров χ' и х χ'' группы G будем понимать характер х, определяемый следующим свойством:

χ (AB) = χ' (A) χ'' (В)

Для любого элемента АÎG, имеем:

χ (АВ) = χ' (АВ) χ'' (АВ) = χ' (А) χ' (В) В· χ'' (А) χ'' (В) = χ(А) χ(В)

Таким образом, получаем χ ' χ '' действительно является характером.

Роль единичного элемента группы G играет главный характер χ₁

Обратным элементом G является:

χ₂ (g₁ g₂) = Ва== Ва= χ₂(g₁) χ₂(g₁)

1.2 Суммы характеров. Соотношение ортогональности

Пусть G тАУ конечная мультипликативная абелева группа порядка h. Рассмотрим сумму:

S = ,

где А пробегает все элементы G, и сумму

Т =

где c пробегает все элементы группы характеров Ĝ.

Рассмотрим чему равна каждая из сумм.

а) Если В-фиксированный элемент группы G и А пробегает все элементы G, то АВ также пробегает все элементы группы G. Следовательно,

SВ·c (В) = c (В) = Ва= Ва= S.

Получили Sc (В) = S, откуда следует, что (c (В) тАУ 1)В·S = 0. Следовательно, возможны два варианта:

1) S = 0, то c (В) тАУ негативный характер

2) S≠0, то c (В) = 1 для каждого элемента ВтВмG и в этом случае c (В)= c₁(В) есть главный характер и сумма S равна порядку h группы G. Таким образом,

S = Ва= {(1.2)

б) Если мы умножим сумму Т на некоторый характер cтАЩ группы Ĝ, то аналогичным образом получим

cтАЩ (А) Т = ВаcтАЩ (А) = Ва= Т,

Следовательно,

1) или Т = 0, то А ≠Е

2) или Т ≠ 0, то cтАЩ (А) = 1 для каждого характера cтАЩтВм G. В этом случае согласно свойству 3Вз 1, имеем А=Е. И тогда Т=h. Таким образом,

Т = = {

1.3 Характеры Дирихле

Пусть m тАУ положительное целое число. Определим числовые характеры по модулю m. Мы знаем, что j(m) приведенных классов вычетов по модулю m образуют мультипликативную абелеву группу порядка h=j(m). Мы можем, следовательно, рассмотреть характер этой группы. Но определение характера для приведенных классов вычета по модулю m можно перенести на множество целых чисел следующим образом. Положим

c(а)= c(А), если аÎА,

где А тАУ приведенный класс вычетов по модулю m. Тогда очевидно, c(а)= c(b) (mod m), и c(ab)= c(а) c(b), если (а, m)=(b, m)=1. Поскольку c(А)¹0 для каждого приведенного класса вычетов А, то c(а)¹0, если (a, m)=1.

Это определение применимо только к целым числам а, которые взаимно просты с m.

Мы можем рассмотреть его на все целые числа, положив

c(а)=0, если (a, m)>1.

Следовательно, характер по модулю m есть арифметическая функция c, обладающая следующими свойствами:

c(а)= c(b), если с=b (mod m)

c(ab)= c(a) c(b) для всех целых a и b

c(а)=0, если (a, m)>1

c(а)¹0, если (a, m)=1

Имеется точно j(m) тАУ количество характеров по модулю m, где j(m) тАУ количество положительных целых чисел, не превосходящих m и взаимно простых с m. Они образуют мультипликативную абелеву группу приведенных классов вычета по mod m. Единичным элементом этой группы будет главный характер c_1, то есть такой характер, что c₁(а)=1, если (а, m)=1. Далее имеем следующее соотношение ортогональности:

= {

= {

Пусть m тАУ положительное целое число. Определим числовые характеры по модулю m. Комплекснозначная функция, определенная для всех целых чисел n, называется числовым характером или характером Дирихле по модулю m, она удовлетворяет следующим условиям:

а) c (n) = 0 тогда и только тогда, когда (n, m) ≠ 1

б) c (n) периодична с периодом m

в) для любых чисел а и b

c (аb) = c (а) c (b)

Функция

c₁(n) = {

является числовым характером и называется главным характером. Остальные числовые характеры по модулю m называются неглавными.

Имеет место следующее утверждение о числовых характерах.

Теорема 1 Существует равно φ(m) числовых характеров по модулю m. Если c = c (n) тАУ числовой характер по модулю m, то:

1) для n, взаимно простых с модулем m, значения c (n) есть корень из 1 степени φ(m).

2) для всех n выполняется неравенство /c (n)/ ≤1

3) Имеет место равенство

{

4) Для каждого целого числа n

Ва= {

Доказательство. Пусть c (n) тАУ некоторый числовой характер по модулю m. Из пункта б) определения следует, что c (n) задает некоторую функцию cтАЩ() = c (n) на мультипликативной группе классов вычетов по модулю m, взаимно простых с m, а именно

cтАЩ() = c (n)

Здесь Ваобозначает класс вычетов по модулю m, содержащий n. Так как c(1) ≠ 0, то cтАЩ() не равняется тождественно нулю, а из пункта в) определения числового характера следует, что cтАЩ() = cтАЩ() = cтАЩ (ab) = c (a) c () = cтАЩ()cтАЩ().

Таким образом, cтАЩ() есть характер модультипликативной группы G_m.

Обратно, по каждому характеру cтАЩ() группы G_m можно построить числовой характер c (n) по модулю m, положив

{

Установленное соответствие является взаимнооднозначным. И все утверждения теоремы 1 следуют из доказанного выше для групповых характеров применительно к группе G_m, если учесть, что порядок группы G_m равен φ(m), где φ(m) тАУ функция Эйлера.

В дальнейшем требуется еще одно утверждение с числовых характерах. Обозначим для каждого c, c ≥ 1

Где суммирование ведется по всем натуральным числам n, не превосходящим c.

Лемма 2. Пусть c (n) тАУ неглавный характер. Тогда для каждого c, c ≥ 1 справедливо неравенство

/S(x)/

Доказательство. Функция c (n) периодична с периодом m и по теореме з

0, так как c≠ c₁

Поэтому, представив [c] тАУ целую часть числа c тАУ в виде [c]=m1+z, 0£z£m, будет иметь

S(c) =S([c])=q

В виду равенства /c(n)/£1 отсюда получили S(c)£z£m

2.
L-функция Дирихле

Пусть х(п) тАУ произвольный характер по модулю m. Рассмотрим ряд

, ВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.1)

члены которого являются функциями комплексного переменного S. В области сходимости он определяет функцию, которая называется L-функцией Дирихле, соответствующей характеру c(n), и обозначается L (s, c).

Лемма 3

1. Если c¹c₁, то ряд (1) сходится в области ReS > 0 и определяемая им функция L (s, c) является аналитической в этой области.

2. Ряд, определяющий L (S, c₁), сходится в области ReS >1. Функция L (S, c₁) является аналитической в области ReS > 1.

Доказательство.

Пусть c(n) тАУ произвольный характер по модулю m, а б тАУ некоторое положительное число. Так как /c(n)/ £ 1, то в области ReS > 1 + б справедливо неравенство

Следовательно, ряд (1) равномерно сходится в области ReS > 1 + б. Определяемая им функция L (S, c) по теореме Вейерштрасса о сумме равномерно сходящегося ряда аналитических функций является аналитической в этой области. Ввиду произвольности 6 это доказывает второе утверждение Леммы.

Для неглавных характеров c(n) потребуется более сложное исследование ряда (1).

Лемма 4 (преобразование Абеля).

Пусть a_n, n=1,2,тАж, тАУ последовательность комплексных чисел, c>1,

А(c)=

а q(t) тАУ комплекснозначная функция, непрерывно дифференцируемая на множестве 1£t£¥

Тогда

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.2)

Если же

то

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.3)

при условии, что ряд в левой части равенства сходится.

Доказательство. Положим А(0)=0 и В(х) равным левой части равенства (2.2). Тогда при любом натуральном N

так как А(0)=0. Далее

поскольку функция А(х) постоянна на каждом полуинтервале n£t

пусть х³1 тАУ произвольное число. Положим N=[x]; значит, N£x£N+1. Тогда А(х)=А(N), B(x)=B(N), а

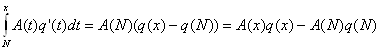
Следовательно,

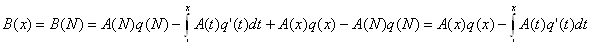
Тем самым доказано, что равенство (2.2) верно и для нецелых чисел значений х.

Равенство (2.3) получаем из равенства (2.2) переходом к пределу при хВо¥. Лемма доказана.

Воспользовавшись леммой 4, получим следующее равенство

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.4)

где

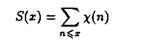
функция, введенная Лемме 4.

Для s = p+it из области ReS = s, где s тАУ некоторое положительное число, пользуясь леммой 4, находим

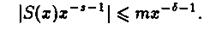
Поэтому интеграл

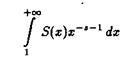
сходится в области ReS > s. Поскольку в этой области выполняется неравенство

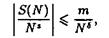
то из равенства (2) следует, что ряд (1), определяющий функцию L (S, x), сходится в области ReS > s. Эти рассуждения справедливы для любого положительного числа s. Значит, ряд (1) сходится в полуплоскости ReS > 0.

Из равенства (2) следует, что в этой полуплоскости для L-функции, соответствующей неглавному характеру c(n), справедливо представление

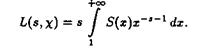
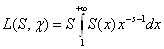ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.5)

так как

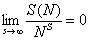
Интеграл, стоящий в правой части равенства (2.5), можно также представить в виде

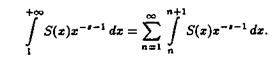ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.6)

Члены ряда (2.6) являются аналитическими функциями в области ReS >s, что следует из равенств

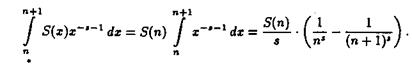
При этом использовано, что на полуинтервале n£х< n+1 функция S(х) принимает значение S(n). Поскольку

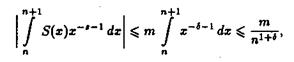
то ряд (2.6) равномерно сходится в области ReS >s. Отсюда, как и выше, получаем, что сумма его, т.е.

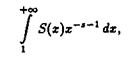
является аналитической функцией (по теореме Вейерштраса) в области ReS >s.

Из представления (2.5) следует теперь, что L (S, x) есть аналитическая функция в полуплоскости ReS >s, а ввиду произвольности S тАУ s и b полуплоскости ReS > 0.

Следствие. Пусть c (n) тАУ произвольный характер. Тогда в области ReS > 1 справедливо равенство

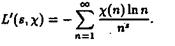ВаВаВаВаВаВаВаВаВаВаВа (2.7)

Это следует из того, что ряд (2.1) по доказанному равномерию сходится в области ReS>1+s, где s>0. Следовательно, по теореме Вейштрасса о равномерно сходящихся рядах аналитических функций в этой области ряд (2.1) можно почленно дифференцировать

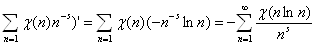
Поэтому в полуплоскости ReS>1+s выполняется равенство (2.7). Так как в этом рассуждении s-любое положительное число, то равенство (2.7) будет справедливо в полуплоскости ReS>1.

Для L-функций имеет место представление в виде бесконечного произведения по простым числам, аналогичное тождеству Эйлера. Рассмотрим вспомогательную Лемму.

Лемма 5. Пусть функция f(n) вполне мультипликативна и ряд

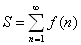ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.8)

абсолютно сходится. Тогда выполняется равенство

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.9)

Доказательство. Отметим прежде всего, что /f(n)/<1 при любом натуральном n>1. В противном случае при каждом mÎN

/f(n)^m/=/f(n)/^m³1,

что противоречит сходимости ряда (2.6). Поэтому при каждом простом р ряд

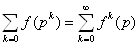
абсолютно сходится, и его сумма как сумма бесконечно убивающей геометрической прогрессии равна (1-f(р))^-1. Кроме этого, в силу абсолютной сходимости, ряды можно перемножить. Перемножая конечное число таких рядов и используя то, что f(n) есть вполне мультипликативная функция, получим

где n_e= p^a тАж p^as и в сумме в правой части равенства содержатся такие и только такие слагаемые f(n_e), что все просты делители n_eне превосходят х. Следовательно, в разности

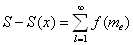
остаются те и только те слагаемые f(m_e), для которых у числа m_e имеется хотя бы один простой делитель р>x. Тогда оценим разность

/S-S(x)/£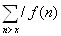

и из абсолютной сходимости ряда (2.8) следует, что

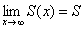
Это доказывает, что бесконечное произведение (2.7) сходится и выполняется утверждение Леммы.

Лемма 6. Для каждого характера c(n) в области ReS > 1 справедливо представление

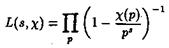
Доказательство. Эта лемма является следствием Леммы 5, поскольку функция c(n) вполне мультипликативна, то есть c(АВ)= c(А) c(В), и выполняется неравенство /c(n)/£ 1 по теореме 1.

Следствие 1. В области ReS > 1 для главного характера c₁(n) по модулю m справедливо равенство

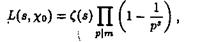ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.10)

и поэтому функция L (S, c₁) может быть аналитически продолжена в область ReS > 0, где она имеет единственный полюс (первого порядка) в точке S=1.

Действительно, по определению главного характера c₁(n) имеет место равенство

Поэтому

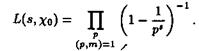
Пользуясь теперь тождеством Эйлера для дзета-функции Римана получаем равенство (2.10). Остальные утверждения легко следуют из этого равенства, поскольку дзета-функция является аналитической в области ReS > 0 с единственным полюсом первого порядка в точке S = 1.

Следствие 2. Для каждого характера c функция L (S, x) не обращается в нуль в области ReS > 1.

Доказательство.

Если s = ReS > 1. то

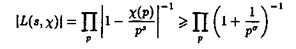
Пользуясь неравенством для дзета-функции Римана, находим

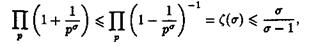
Получаем:

L (S,c) ≥ 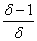> 0

Теперь докажем утверждения, что L тАУ функция, соответствующая неглавному характеру c, точке S =1 отлична от нуля.

Теорема 2. Если c тАУ неглавный характер, то L (1, c)≠0

Для доказательства рассмотрим 2 случая

1. Пусть характер c тАУ комплексное число, не является действительным. Тогда характер c²(n) не является главным. В этом случае доказательство теоремы будет основываться на тех же идеях, что и доказательство отсутствия нулей дзета тАУ функции на прямой ReS=1.

Лемма7. Пусть 0<ч<1, а х тАУ действительное число, тогда выполняется неравенство /(1 тАУ ч)³ (1 тАУ че^ix)⁴ (1 тАУ че^2ix)/^-1 ≥ 1

Доказательство.

Для всех z из круга /z/<1 имеет место расположение

тАУ ln (1 тАУ z) =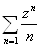(2.11)

Так как ln(t) = Re lnt, то обозначая М (ч φ), левую часть неравенства (2.11), получим

lnM (ч φ) = 3ln (1 тАУ ч) тАУ 4 ln (1 тАУ чеⁱ⁴) тАУ ln (1 тАУ че²ⁱ⁴) = тАУ 3ln (1-ч) тАУ 4Reln/1 тАУ чеⁱ⁴/ тАУ Reln/1 тАУ че²ⁱ⁴/=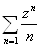rc (3+4e)^inl/1-reⁱ⁴/= 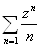(3+4cosnl+2cos2nl)= 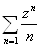(2+4cosa+1+cos2a)=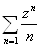1 (1+cosa)²³0

ln=M (r, l)=³0

Следовательно, M (r, l)=³1 доказана.

Из леммы 7 следует, сто при любом действительном S>1 выполняется равенство:

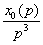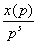L³(8, c₁) L⁴(S, c) 4 (S, c⁴) 1 = П (1- )³(1- )⁴(1- 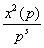)|^-1Ва (2.12)

Получая в лемме ч = р^-s, т.е.

0< ч = c₁(р)<1

0< р^-s<1

c (р) р^-s = чеⁱ⁴, в силу того что c (р) тАУ комплексное

c (р) р^-s= че²ⁱ⁴

Получаем, что каждый сомножитель в правой части равенства (f) не меньше 1 и, следовательно, при любом S>1 выполняется равенство:

|L³(Sc₁) В· L⁴(Sc) L (Sc²)| ≥ 1ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.13)

Допустим, что для некоторого характера c (c²≠c₁) выполняется равенство

L (1, c) = 0ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.14)

Оценим сверху левую часть неравенства. Из оценки дзета-функции Римана

ξ(S) ≤ 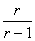, следует, что при S тВм R, S>1 выполняется неравенство

а) 0 < 4 (S, c₁) =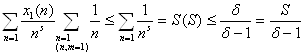

получили 01)≤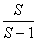

б) Функция L (S, c) разложим в ряд Тейлора

L (S, c) = C_p + C₁ (S тАУ 1) + C₂(S тАУ 1)² +тАж + C_n(S тАУ 1)ⁿ +тАж

Предположим, что у нее есть нуль L (1, c) = 1; тогда С₀ = 0

Перепишем разложение L тАУ функции в ряд

L(S^c) = C_к (S тАУ 1)^к + С_к+1(S тАУ 1)^к+1 = (S тАУ 1)¹ (C_к + С_к+1(S -1)+тАж.), где к≥1, С_к ≤ 0, т. к. S>1

| L (S, c)| = |S тАУ 1|^k| C_k + C_k+1(S тАУ 1) +тАж.| ≤ 2 C_k|S тАУ 1)^k, при |S тАУ | < r

Функция L (S, c²) в точке S = 1 не имеет полюса, следовательно не имеет особенности. Это в силу того, что c комплексное и c²≠c₁

Получаем неравенство:

L (S, c²) ≤ C,

При условии | S тАУ 1|< δ

Учитывая все неравенства и оценки

| L³ (S, c) L⁴(S, c) L (S, c²)| = (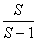)³ В· 2⁴ |C_k|⁴ (S тАУ 1)^4kВ· C≥1

Следовательно, это неравенство становится противоречивым, если перейти к пределу при S→1+0. Полученное противоречие показывает, что равенство (2.14) не выполняется.

2. Рассмотрим c тАУ вещественный характер, т.е. принимающий только вещественные значения, несовпадающий с главным характером

Лемма 8. Пусть c тАУ вещественный характер.

Рассмотрим функцию

F(S) = ξ(S) L (S, x)ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.15)

Докажем, что если Re S>1, то

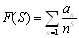ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.16)

представляется рядом Дирихле, которого справедливы следующие утверждения:

1) Все коэффициенты а_n≥ 0

2) при n=k², k тВм / N(N)/ а_n≥1

3) В области ReS<1 можно почленно дифференцировать, то есть

F ^(k) (S)= 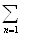(-1)^k(ln n)^k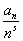Ваk=1,2тАж; ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.17)

4) Ряд (1) в точке S=1/2 расходится.

Доказательство. В области ReS > 1 ряды, определяющие функции S(S) и L (S,c), абсолютно сходятся, поэтому их можно перемножить:

где

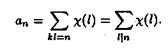ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.19)

Пусть 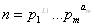- расположение числа n в произведение простых сомножителей. Тогда все натуральные делители l числа n имеют вид

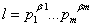
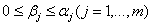
поэтому из равенства (14) находим, что

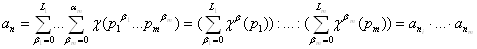
где a_{ni =} 1+ c (p_i)+ тАж +c^Li (p_i), i=1,тАж, mВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.21)

так как c тАУ вещественный характер, то он может принимать только три значения: 0, 1, -1. Из равенства (2.21) следует, что

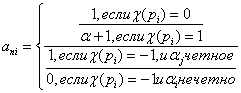ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.22)

Во всех случаях числа a_ni³0, а значит, и a_n=a_n1 тАж a_nm³0

Если же число п является полным квадратом, то

N=k²=p_/^2g тАж p_m^2g,

и из равенств (2.20) и (2.22) следует, что а_n ³1

При любом s > 0 в области ReS> 1 +s выполняется неравенство

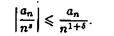
Ряд (2.18) сходится в области ReS > 1. Поэтому по признаку Вейерштрасса ряд (2.16) сходится равномерно в области ReS > 1 + s, а по теореме Вейерштрасса его можно в этой области почленно дифференцировать любое число раз. Следовательно, в области ReS > 1 +s выполняется равенство (2. 17), а в силу произвольности s оно выполняется и в области ReS > 1.

Однако ряд (39) расходится, так как по второму утверждению леммы

Ряд (2.16) при S = 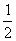Ваимеет неотрицательные члены. Поэтому, если бы он сходился, то также сходился бы ряд

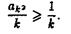ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.23)

Следовательно, ряд (2.23) расходится. Лемма доказана.

Переходим непоредственно к доказательству второго случая теоремы. Допустим, что L (1,c) = 0. Тогда полюс дзета-функции будет компенсироваться в произведении S(S) L (S, c) нулем функции L (S, c).

Поэтому функция (2.15) F(S) будет аналитической в области ReS > 0 так как в точке S=1 у F(z) тАУ устраненная особая точка. Следовательно, ее можно разложить в ряд Тейлора в точке S = 2:

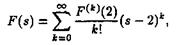ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2. 24)

радиус сходимости которого не меньше 2 R³2/

Из равенств (2.17), в частности S=2, находим

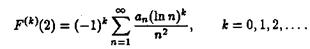ВаВаВаВаВаВаВаВаВаВаВаВа (2.25)

В радиусе сходимости будет брать не все S, а только вещественные ReS=s S=sÎ(0,2). Пользуясь разложениями (18) и (19), находим

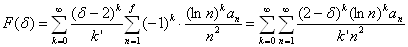
Члены двойного ряда неотрицательны, поэтому он сходится абсолютно, и в нем можно поменять порядок суммирования. Тогда

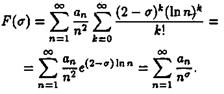
Следовательно, ряд (2.16) сходится во всех точках, s < (, 0, 2), и в точке 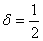, а это противоречит четвертому утверждению леммы. Поэтому L (S,c)¹0/

Этим завершается доказательство теоремы

По следствию 2 леммы 2 функция 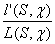Ваявляется аналитической в области ReS > 1. Для дальнейшего доказательства теоремы Дирихле нам будет необходимо представление этой функции в виде ряда, аналогичного ряда (2.16).

Лемма. Для каждого характера c(n) в области ReS > 1 справедливо равенство

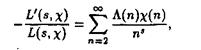ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2.26)

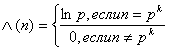
Доказательство.

Так как S=s+it имеет место неравенство

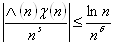
получаем, что ряд стоящий в правой части равенства (2.26), абсолютно сходится в области s>1. Умножим этот ряд на ряд определяющий L (S, c). Получили

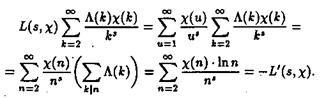
Предпоследнее равенство имеет место ввиду равенства 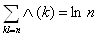), а последнее тАУ по следствию из леммы 3, равенство 2.7.

3. Доказательство теоремы Дирихле

Теорема. Если разность и первый член арифметической прогрессии есть взаимно простые натуральные числа, то она содержит бесконечное множество простых чисел.

Доказательство.

Рассмотрим равенство (2.26), которое справедливое по Лемме в области ReS > 1. Поскольку 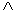(n) = 0 для всех n, не являющихся степенями простых чисел, то все отличные от нуля члены ряда в правой части (2.26) имеют вид

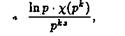
где р тАУ простое и k тАУ натуральное числа. Ряд (2.26) абсолютно сходится, следовательно, его можно представить в виде двойного ряда) и, значит, в области ReS > 1

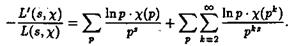ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.1)

Второе слагаемое в правой части этого равенства равномерно ограничено по s в области ReS³3/4. Действительно, если S=p+it, p³3/4, то

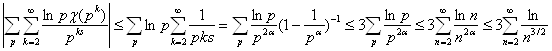
Следовательно, при SВо1+0 для каждого характера c имеет место равенство

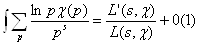ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.2)

Здесь и в дальнейшем s Во 1 + o обозначает, что S стремится к 1 по действительной оси справа.

Пусть u тАУ некоторое натуральное число, удовлетворяющее сравнению

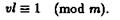ВаВаВаВаВаВаВаВаВаВаВаВаВа (3.3)

Умножим обе части равенства (3.2) на c(u) и просуммируем получившиеся равенства по всем числовым характерам c. Тогда получим

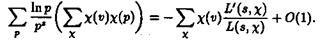ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.3)

Если простое число р удовлетворяет сравнению р ºl (mod m), то pu ≠ 1 (mod m), и по теореме 1

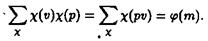
Если же p≠l (mod m), то pu≠ 1 и по той же теореме

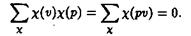
Таким образом, равенство (3.3) можно переписать в виде

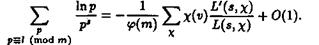ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.4)

По лемме 3 и теореме 2 для неглавного характера c функция 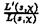Ваявляется аналитической в точке S = 1. Поэтому для таких характеров при S Во1 + 0 имеем

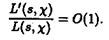ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3.5)

По следствию 1 леммы 4 функция L (S, c₁) имеет в точке S=1 полюс первого порядка. Значит, при SВо1+0

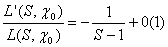ВаВаВаВаВаВаВаВаВаВаВаВа (3/6)

Учитывая равенства (3.5) и (3.6.) из равенства (26) получаем, что

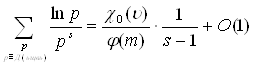
Так как число u удовлетворяет сравнению (3.3), то (u, m) = 1 и c₀(u)=1. Итак, при SВо1+0

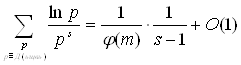(3.7)

Правая часть равенства а (3.7) при SВо1+0 имеет бесконечный предел. Значит, сумма, стоящая в левой части этого равенства, имеет бесконечное множество слагаемых. Поэтому существует бесконечное множество простых чисел, удовлетворяющих сравнению

pºe (mod m)

Теорема Дирихле доказана.

Вместе с этим смотрят:

РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора

РЖнтегральнi характеристики векторних полiв

РЖнтерполювання функцiй

Автокорреляционная функция. Примеры расчётов

Аксонометричнi проекцii