Поняття фракталiв
План
I. Вступ
1.1 Фрактал. РЖсторiя його виникнення
1.2 Види фракталiв та методи iх створення
1.3 Типи самоподiбностi у фракталах
1.4 Розмiрнiсть фракталiв
II. Основна частина
2.1Класифiкацiя алгоритмiв створення фракталiв
2.2 Системи РЖтерiруiмих Функцiй
2.3 Стиснюючi афiннi перетворення
2.4 Метод простоi замiни
2.4.1 Серветка Серпiнського
2.4.2 Дракон Хартера-Хейтуея
2.5 Алгебраiчнi фрактали
2.6 Графiки функцiй комплексноi змiнноi
2.7 Формули побудови фракталiв
2.7.1 Рiзновид алгебраiчних фракталiв тАФ басейни Ньютона
2.7.2 Множина Жюлiа та Мандельброта
III. Висновок
IV. Використана лiтература
РЖ Вступ
1.1 Фрактал. РЖсторiя його виникнення
Все, що створено людиною, обмежено площинами. Коли зустрiчаiться обтАЩiкт у природi, то спочатку можна побачити, що описати його форму можна лише наближено й допоможуть в цьому фрактали. Де закiнчуються правильнi форми Евклiдовоi геометрii, там зустрiчаються фрактали.
Фракта́л (лат. fractus тАФ подрiбнений, дробовий) тАУ нерегулярна, самоподiбна структура. У широкому розумiннi фрактал означаi фiгуру, малi частини якоi в довiльному збiльшеннi i подiбними до неi самоi (мал.1).
Об'iкти, якi тепер називаються фракталами, дослiджувались задовго до того, як iм було дано таку назву. В етноматематицi, наприклад в роботах Рона Еглаша "Африканськi Фрактали", задокументовано поширенi фрактальнi геометричнi фiгури в мистецтвi тубiльцiв. У 1525 роцi нiмецький митець Альбрехт Дюрер опублiкував свою працю тАЬКерiвництво ХудожникатАЭ, один iз роздiлiв якоi маi назву "Черепичнi шаблони, утворенi пентагонами". Пентагон Дюрера багато в чому i схожим на килим Серпiнського, але замiсть квадратiв використовуються п'ятикутники. Джексон Поллок (американський експресiонiст 50-тих рокiв) малював об'iкти, дуже схожi на фрактали.
РЖдею "рекурсивноi самоподiбностi" було висунуто фiлософом Лейбнiцом, який також розробив багато з деталей цiii iдеi. У 1872 Карл Веiрштрасс знайшов приклад функцii з неiнтуiтивною особливiстю, скрiзь неперервноi, але нiде недиференцiйованоi тАФ графiк цiii функцii тепер називався б фракталом. У 1904 Хельга Фон Кох, незадоволений занадто абстрактним та аналiтичним означенням Веiрштрасса, розробив бiльш геометричне означення схожоi функцii, яка тепер маi назву снiжинки Коха. РЖдею самоподiбних кривих, котрi складаються iз частин, схожих на цiле, було далi розвинено Полем П'iром Левi, який у своiй роботi "Кривi та поверхнi на площинi та у просторi", виданiй 1938 року, описав нову фрактальну криву, вiдому тепер як Крива Левi (мал.2 а, б, в).
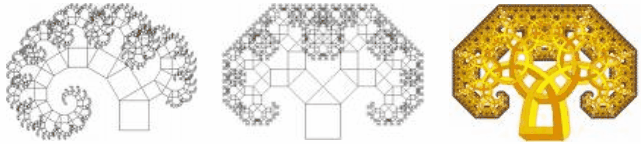
а) б) в)
Мал.2
ТРеорг Кантор навiв приклади пiдмножин дiйсних чисел iз незвичними властивостями тАФ цi множини Кантора тепер також визнаються як фрактали.
РЖтерацiйнi функцii на комплекснiй площинi дослiджувались в кiнцi XIX та на початку XX столiття Анрi Пуанкаре, Фелiксом Кляйном, П'iром Фату та ТРастоном Жюлiа. Проте за браком сучасноi комп'ютерноi графiки у них забракло засобiв вiдобразити красу багатьох iз вiдкритих ними об'iктiв.
У 1975 роцi Мандельброт використав слово фрактал як назву для об'iктiв, розмiрнiсть Хаусдорфа яких i бiльшою за топологiчну розмiрнiсть, наприклад Крива Хильберта (мал.3 а,б,в,г).
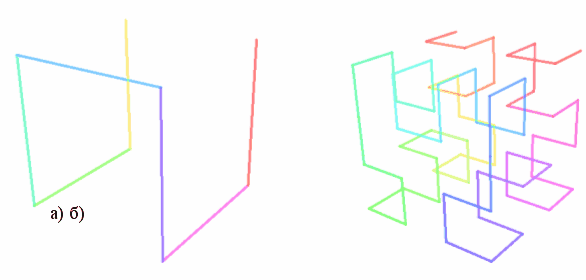

Мал.3
1.2 Види фракталiв та методи iх створення
РЖснують три поширенi методи створення (генерування) фракталiв:
Перший метод тАФ iтерацiйнi функцii, якi будуються вiдповiдно до фiксованого правила геометричних замiщень, в результатi яких утворюються геометричнi фрактали, наприклад: снiжинка Коха (мал.4).
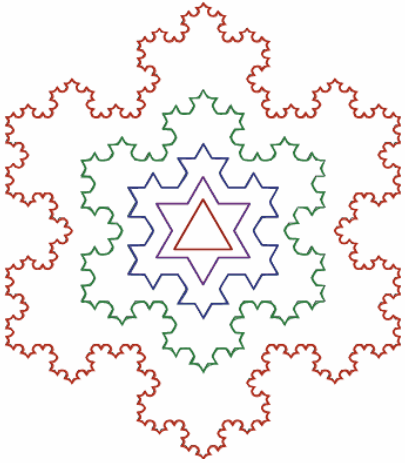
ВаМал.4
А також множина Кантора, килим Серпiнського, трикутник Серпiнського, крива Пiано, крива Коха, крива дракона, Т-Квадрат та губка Менгера i прикладами геометричних фракталiв.
Другий метод тАФ рекурентнi вiдношення, це фрактали, що визначаються рекурентним вiдношенням у кожнiй точцi простору (такому як площина комплексних чисел). Отриманi таким методом фрактали називають алгебраiчними.
Прикладами алгебраiчних фракталiв i множина Мандельброта (мал.5), палаючий корабель та фрактал Ляпунова.

Мал.5
Третiй метод тАФ випадковi процеси, це фрактали, що генеруються з використанням стохастичних, а не детермiнованих процесiв, наприклад: фрактальнi ландшафти (мал.6 а,б,в,г,д), траiкторiя Левi та броунiвське дерево.

Мал.6.
1.3 Типи самоподiбностi у фракталах
Розрiзняють три типи самоподiбностi у фракталах:
Точна самоподiбнiсть тАФ це найсильнiший тип самоподiбностi; фрактал виглядаi однаково при рiзних збiльшеннях. У фракталiв, згенерованих з використанням iтерацiйних функцiй, часто виявляiться точна самоподiбнiсть.
Майже самоподiбнiсть тАФ слабка форма самоподiбностi; фрактал виглядаi приблизно (але не точно) самоподiбним при рiзних збiльшеннях. Майже самоподiбнi фрактали мiстять малi копii цiлого фракталу у перекручених та вироджених формах. Фрактали, згенерованi з використанням рекурентних вiдношень, зазвичай i майже (але не точно) самоподiбними.
Статистична самоподiбнiсть тАФ це найслабкiша форма самоподiбностi; фрактал маi чисельнi або статистичнi мiри, що зберiгаються при збiльшеннi. Найприйнятнiшi означення "фракталiв" просто мiстять в собi деякий вид статистичноi самоподiбностi (розмiрнiсть фракталу, саме по собi, i чисельною мiрою, що зберiгаiться при збiльшеннi). Ймовiрнiснi фрактали i прикладами фракталiв, якi i статистично, але не майже й не точно самоподiбними.
1.4 Розмiрнiсть фракталiв
У евклiдовоi геометрii i поняття розмiрностi: розмiрнiсть крапки тАФ нуль, вiдрiзка та кола тАФ одиниця, круга i сфери тАФ два, кулi тАФ три. З одновимiрними об'iктами ми пов'язуiмо поняття довжини, з двовимiрними - площi i так далi. Але як можна уявити собi множину з розмiрнiстю 3/2? Мабуть, для цього потрiбно щось промiжне мiж довжиною i площею, i якщо довжину умовно назвати 1-мiрою, а площа - 2-мiрою, то потрiбна (3/2) -мiра.
У 1919 роцi Ф. Хаусдорф дiйсно визначив таку а-мiру i на цiй основi кожнiй множинi в евклiдовому просторi пiдставив число, назване iм метричною розмiрнiстю. Вiн же навiв першi приклади множин з дробовою розмiрнiстю. Виявилось, що дробову розмiрнiсть мають канторова множина, крива Коха i iншi екзотичнi об'iкти, до недавнього часу маловiдомi за межами математики.
Оскiльки фрактал складаiться з нескiнченного числа елементiв, що повторюються, неможливо точно вимiряти його довжину. Це означаi, що чим точнiшим iнструментом ми будемо його вимiрювати, тим бiльшою виявиться його довжина. Тодi як гладка евклiдова лiнiя заповнюi в точностi одновимiрний простiр, фрактальна лiнiя виходить за межi одновимiрного простору, вторгаючись у двовимiрне. Таким чином, фрактальна розмiрнiсть кривоi Коха знаходитиметься мiж 1 i 2. Найдивовижнiшим виявляiться те, що й багато природних об'iктiв володiють нiби дробовою розмiрнiстю, хоча, вiдверто кажучи, для природних об'iктiв таку розмiрнiсть обчислити неможливо. Правильнiше сказати, що в певних дiапазонах спостереження природнi об'iкти, що виникли в результатi довгоi дифузii й абсорбцii, схожi на фрактальнi множини. Наприклад, розмiрнiсть побережжя лежить мiж 1,01 i 1,6, а кровоносноi системи людини тАФ мiж 3,4 i 3,6
РЖРЖ Основна частина
2.1Класифiкацiя алгоритмiв створення фракталiв
Бенуа Мандельброт в своiх книгах навiв яскравi приклади вживання фракталiв до пояснення деяких природних явищ. Мандельброт придiлив велику увагу цiкавiй властивостi, якою володiють багато фракталiв. Рiч у тому, що часто фрактал можна розбити на скiльки завгодно малi частини так, що кожна частина виявиться просто зменшеною копiiю цiлого. РЖнакше кажучи, якщо ми дивитимемося на фрактал в мiкроскоп, то iз здивуванням побачимо ту ж саму картину, що i без мiкроскопа. Це властивiсть самоподiбностi рiзко вiдрiзняi фрактали вiд об'iктiв класичноi геометрii.
Необхiдно вiдзначити, що властивiсть самоподiбностi характерна лише для регулярних фракталiв.Багато регулярних фракталiв будуються шляхом нескiнченного повторення декiлькох простих операцiй - замiною одного елементу деякою комбiнацiiю iнших, йому подiбних. Потiм ця ж операцiя повторюiться з кожним з цих елементiв, i так далi до нескiнченностi. На методi простоi замiни заснований перший алгоритм побудови фракталiв.
ВаВиникаi питання, чи не можна цю "процедуру замiни" перекласти мовою математичних формул. Таким чином, в серединi 80-х рокiв з'явився метод Систем РЖтерiруiмих Функцiй - СРЖФ (Iterated Function System - IFS) як простий засiб здобуття фрактальних структур. Таким чином, деякi з вищеперелiчених фракталiв можна отримати за допомогою методу СРЖФ. Метод Систем РЖтерiруiмих функцiй i основою для другого алгоритму побудови фрактальних структур. Замiсть детермiнованого способу побудови регулярних фракталiв в алгоритм створення фрактальних структур був включений деякий елемент випадковостi, що приводить до побудови випадкових фракталiв. Багато фракталiв можуть бути отриманi за допомогою цих двох алгоритмiв. Тодi в першому випадку вони побудованi як регулярнi фрактали, а в другому як випадковi.
Одним з найбiльш яскравих прикладiв серед рiзних систем iтерiруiмих функцiй i вiдкрита система М. Бранслi з чотирьох стискуючих афiнних перетворень, аттрактором для якоi i множина точок, яка дуже нагадуi по формi зображення листа папоротi.

Мал.7
Третiм алгоритмом створення фрактальних об'iктiв на площинi i використання комплексних вiдображень, що зiставляють одному комплексному числу iнше комплексне число за деяким iтерацiйним правилом. Прикладом фрактала отриманого за допомогою комплексних вiдображень i множина Жюлiа (мал.7).
2.2 Системи РЖтерiруiмих Функцiй
У евклiдовом просторi ![]() Вавiдстань
Вавiдстань ![]() (x;y) мiж точками x=(
(x;y) мiж точками x=(![]() ;
;![]() ) i y=(
) i y=(![]() ;
;![]() ) визначаiться за допомогою наступноi формули
) визначаiться за допомогою наступноi формули

Вiдстань в просторi ![]() Ваможна також вимiрювати функцiiю
Ваможна також вимiрювати функцiiю ![]() (x;y)=|
(x;y)=|![]() -
-![]() |+|
|+|![]() -
-![]() |.
|.
ВаДвi приведенi функцii, будучи вимiрами вiдстанi, по-рiзному визначають вiдстанi мiж двома точками. РЖснують чотири основнi властивостi функцii вiдстанi:
ü вiдстанi вiд точки x до точки y i вiд точки y до точки x рiвнi: d(x;y)=d(у;x);
ü вiдстань вiд точки x до цiii ж точки x дорiвнюi нулю: d(x;x)=0;
ü вiдстань по прямiй - це найкоротша вiдстань мiж двома точками: d(x;y) <=d(x;z)+d(z;y);
ü для двох точок x i у функцiя вiдстанi маi бути дiйсною, скiнченою i додатною : ![]() .
.
Функцiя вiдстанi, що задовольняi даним властивостям, називаiться метрика.
Метричний простiр (X,d) - множина точок X разом з метрикою d, визначеною на X.
Перетворення - зiставлення, згiдно заздалегiдь визначеному правилу, точцi в одному просторi точки в iншому (можливо i в тому ж самому просторi).
![]() Вiдображення, це перетворення, яке переводить простiр X1 в простiр X2 i позначаiться fn: X1 X2.
Вiдображення, це перетворення, яке переводить простiр X1 в простiр X2 i позначаiться fn: X1 X2.
![]() Стиснююче вiдображення - перетворення
Стиснююче вiдображення - перетворення ![]() Вав метричному просторi X1 X2 за умови iснування коефiцiiнта стиснення перетворення f: 0
Вав метричному просторi X1 X2 за умови iснування коефiцiiнта стиснення перетворення f: 0![]() s<1 такого, що d(f(x1),f(x2))
s<1 такого, що d(f(x1),f(x2)) ![]() sd(x1,x2) для всiх
sd(x1,x2) для всiх ![]()
![]() Система iтерiруiмих функцiй (Iterated Function System) складаiться з повного метричного простору (X,d) i скiнченноi множини стиснюючих вiдображень fn: X1 X2 з коефiцiiнтами стиснення Sn.
Система iтерiруiмих функцiй (Iterated Function System) складаiться з повного метричного простору (X,d) i скiнченноi множини стиснюючих вiдображень fn: X1 X2 з коефiцiiнтами стиснення Sn.
2.3 Стиснюючi афiннi перетворення

Мал. 8.
Перш нiж розкривати змiст поняття - стиснюючi афiннi перетворення, розглянемо лiнiйне перетворення ![]() Вана комплекснiй площинi Z, яке переводить рiвностороннiй трикутник з довжиною сторони рiвнiй одиницi в рiвностороннiй трикутник в два рази меншого розмiру представлений на мал. 8.
Вана комплекснiй площинi Z, яке переводить рiвностороннiй трикутник з довжиною сторони рiвнiй одиницi в рiвностороннiй трикутник в два рази меншого розмiру представлений на мал. 8.
Розглянуте вище лiнiйне перетворення на комплекснiй площинi i окремим випадком афiнного перетворення площини
xn+1=axn+byn+e
yn+1=cxn+dyn+f
Його можна подати в матричному виглядi
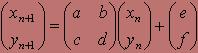
Так, наприклад, розглянуте перетворення можна записати у виглядi
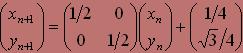
У загальному випадку афiнне перетворення на площинi задаiться шiстьма незалежними дiйсними числами. Два числа e i f описують звичайну трансляцiю, а чотири числа а, b, с, d задають довiльне лiнiйне перетворення при незмiнному положеннi початку координат (0;0).
2.4 Метод простоi замiни
2.4.1 Серветка Серпiнського
Фрактал серветка Серпiнського може бути побудований як за допомогою методу простоi замiни, який застосовують для побудови регулярних фракталiв, так i за допомогою методу IFS.
ВаРозглянемо алгоритм побудови, заснований на методi простоi замiни. Правильний трикутник дiлений середнiми лiнiями на чотири рiвнi трикутники i внутрiшнiсть центрального викидаiмо. З трьома трикутниками, що залишилися, робимо те ж саме i так нескiнченне число разiв. Пiсля певного числа викидань залишаiться множина S, представлена на мал. 9, яка i серветкою Серпiнського.

Мал.9.
Фрактальна розмiрнiсть серветки Серпiнського пiдраховуiться по формулi D=ln3/ln2=1,5849. Серветка маi нульову площу, оскiльки неважко перевiрити, що в процесi ii побудови була виключена площа, в точностi рiвна площi вихiдного трикутника. Про це ж свiдчить i значення фрактальноi розмiрностi D<2, яка менше розмiрностi площини, на якiй знаходиться цей об'iкт.
Всiм вiдомий трикутник Паскаля (мал.10) за допомогою якого обчислюють коефiцiiнти розкладу виразу виду ![]() . Починаючи з трикутника, що складаiться з одиниць, обчислюють значення на кожному наступному рiвнi шляхом додавання сусiднiх чисел; останньою ставлять одиницю.
. Починаючи з трикутника, що складаiться з одиниць, обчислюють значення на кожному наступному рiвнi шляхом додавання сусiднiх чисел; останньою ставлять одиницю.

Мал.10
Таким чином можна наприклад визначити, що:
![]() .
.
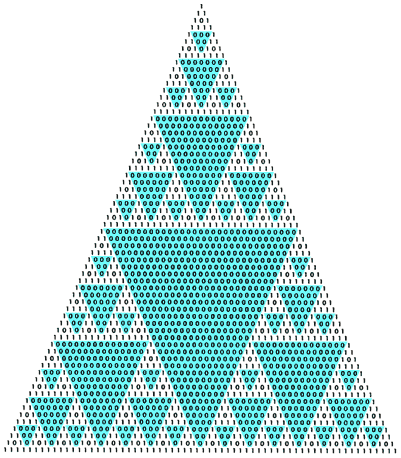
Мал.11
Цей трикутник можна перетворити на привабливий фрактальний вiзерунок (мал.11), якщо замiнити непарнi коефiцiiнти одиницями, а парнi тАФ нулями.
Вiзерунок демонструi властивостi коефiцiiнтiв, що використовуiться при ВларифметизацiiВ» комптАЩютерних програм, що перетворюi iх в алгебраiчнi рiвняння.
2.4.2 Дракон Хартера-Хейтуея
Для бiльшостi регулярних фракталiв фрактальна розмiрнiсть D менша, нiж розмiрнiсть d того простору, в якому знаходиться даний фрактальний об'iкт. Нерiвнiсть D < d вiдображаi факт некомпактностi фрактала, причому чим бiльше розрiзняються величини D i d, тим бiльше рихлим i фрактал. РЖснують фрактали, якi щiльно заповнюють простiр, в якому вони знаходяться, так що iх фрактальна розмiрнiсть D = d. Одним з прикладiв такого роду i кривi Пеано (Peano curves). Дракон Хартера-Хейтуея (мал.12) i прикладом кривоi Пеано, для якоi область, яку вона заповнюi на площинi, маi химерну форму.

Мал.12
Першi чотири кроки його побудови представлено на мал.12
Як випливаi з мал.13 кожний з вiдрiзкiв прямоi на наступному кроцi замiнюiться на два вiдрiзки, створюючих бiчнi сторони рiвнобедреного прямокутного трикутника, для якого вихiдний вiдрiзок був би гiпотенузою. В результатi вiдрiзок як би прогинаiться пiд прямим кутом. Напрям прогину чергуiться. Перший вiдрiзок прогинаiться вправо (по ходу руху злiва направо), другий - влiво, третiй - знову управо i так далi На мал.13 пунктиром показана конфiгурацiя попереднього кроку. Таким чином, пiсля кожного кроку число наявних вiдрiзкiв подвоюiться, а довжина кожного вiдповiдно зменшуiться вдвiчi. Тому фрактальна розмiрнiсть кривоi, що утворюiться в результатi (пiсля нескiнченного числа крокiв), рiвна 2.
Для реалiзацii вказаного вище алгоритму побудови необхiдно перейти до комплексних чисел ZA, ZB и ZC (Мал.14).
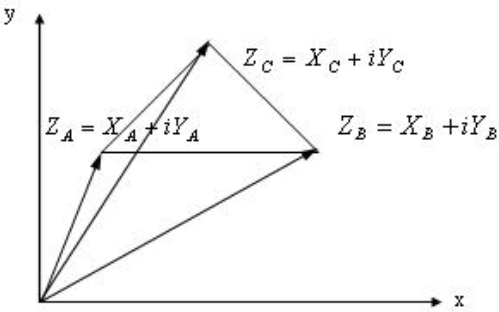
Мал.13
Для знаходження координат точки C представимо комплекснi числа в тригонометричнiй формi. Знаходження координат точки C представлене формулами 1-8.
![]() Ва(1)
Ва(1)
![]() Ва(2)
Ва(2)
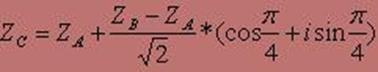 Ва(3)
Ва(3)
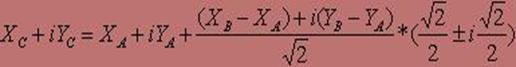 (4)
(4)
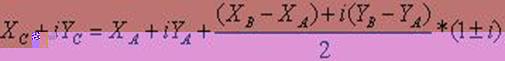 (5)
(5)
![]() Ва(6)
Ва(6)
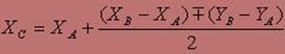
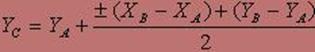
Гранична фрактальна крива (коли прямуi до нескiнченностi) називаiться драконом Хартера-Хейтуея. У машиннiй графiцi використання геометричних фракталiв необхiдно для отримання зображень дерев, кущiв, берегових лiнiй. Двовимiрнi геометричнi фрактали використовуються для створення обтАЩiмних текстур (малюнка на поверхнi обтАЩiкту).
2.5 Алгебраiчнi фрактали
Це найкрупнiша група фракталiв. Отримують iх за допомогою нелiнiйних процесiв в -мiрних просторах. Найбiльш дослiдженi двомiрнi процеси. РЖнтерпретуючи нелiнiйний iтерацiйний процес, як дискретну динамiчну систему, можна користуватися термiнологiiю теорii цих систем: фазовий портрет, сталий процес, аттрактор та iншi.
ВаВiдомо, що нелiнiйнi динамiчнi системи володiють декiлькома стiйкими станами. Той стан, в якому виявилася динамiчна система пiсля деякоi кiлькостi iтерацiй, залежить вiд ii початкового стану. Тому кожен стiйкий стан (або як говорять - аттрактор) володii деякою областю початкових станiв, з яких система обов'язково попаде в данi кiнцевi стани. Таким чином фазовий простiр системи розбиваiться на областi тяжiння аттракторiв. Якщо фазовим i двомiрний простiр, то забарвлюючи областi тяжiння рiзними кольорами, можна отримати кольоровий фазовий портрет цiii системи (iтерацiйного процесу). Змiнюючи алгоритм вибору кольору, можна отримати складнi фрактальнi картини з химерними багатокольоровими узорами. Несподiванкою для математикiв стала можливiсть за допомогою примiтивних алгоритмiв породжувати дуже складнi нетривiальнi структури.

Мал.14.
Наприклад, фрактал Ньютона, який штрихуiться вiдповiдно до кiлькостi iтерацiй (мал.14).
2.6 Графiки функцiй комплексноi змiнноi
Комплекснi числа можна трактувати як точки на площинi. Тодi множину Мандельброта можна побудувати у просторi ![]() .
.
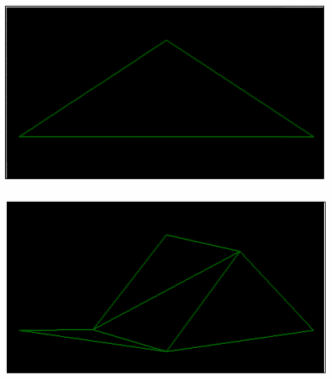
Взагалi, графiк дiйсноi функцii можна побудувати в двомiрному просторi (2D), на площинi xOy. Це багатьом знайомо й звично(мал.15 а,б):

Мал.15(а,б)
![]() Графiк комплексноi функцii можна було б побудувати в чотиривимiрному (4D) просторi (двi координати потрiбно для зображення
Графiк комплексноi функцii можна було б побудувати в чотиривимiрному (4D) просторi (двi координати потрiбно для зображення ![]() , i двi тАУ для
, i двi тАУ для ![]() Ва).
Ва).
![]()
![]()
![]()
![]() На жаль, переважна бiльшiсть людей стикаються з серйозними проблемами при уявi чотиривимiрного простору.. Тому, одне з хитрощiв, зазвичай вживане, полягаi в наступному: графiк будуiться в тривимiрному (3D) просторi. Вiсь Ox вiдповiдаi за , вiсь Oy тАУ за , вiсь Oz тАУ затАжтАж. Для зображення використовуiться колiр отриманоi 3D-крапки. Колiр береться iз заздалегiдь сформованоi кольоровоi шкали (градiiнта).
На жаль, переважна бiльшiсть людей стикаються з серйозними проблемами при уявi чотиривимiрного простору.. Тому, одне з хитрощiв, зазвичай вживане, полягаi в наступному: графiк будуiться в тривимiрному (3D) просторi. Вiсь Ox вiдповiдаi за , вiсь Oy тАУ за , вiсь Oz тАУ затАжтАж. Для зображення використовуiться колiр отриманоi 3D-крапки. Колiр береться iз заздалегiдь сформованоi кольоровоi шкали (градiiнта).
Ось декiлька прикладiв (мал.16 а,б) для ![]() :
:
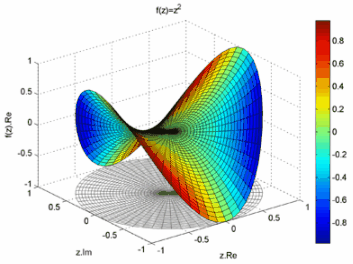
а)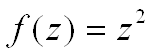
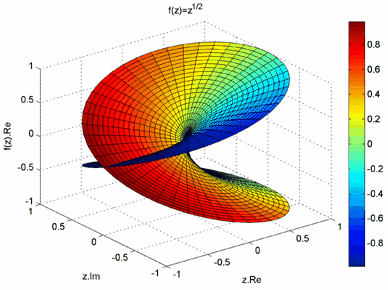
б)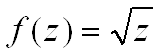
Мал.16 (а,б)
Для наочностi пiд отриманою ВлповерхнеюВ» зображено множина значень ![]() Ва( (Влкругла тiньВ»).
Ва( (Влкругла тiньВ»).
2.7 Формули побудови фракталiв
2.7.1 Рiзновид алгебраiчних фракталiв тАФ басейни Ньютона (мал.17).
p(z) = 0, p(z) = ![]() Ва− 1,
Ва− 1,
якi будуються за формулою:
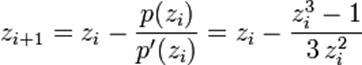
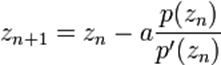
Узагальнена формула , де a тАФ будь-яке комплексне число.

2.7.2 Множина Жюлiа та Мандельброта
Позначимо через ![]() Ваплощину комплексних чисел, а через
Ваплощину комплексних чисел, а через ![]() тАФ риманову сферу
тАФ риманову сферу ![]() . Розглянемо процес
. Розглянемо процес![]() , де
, де ![]() Вата
Вата ![]() . Взявши будь-яке число
. Взявши будь-яке число ![]() , пiднесемо до квадрату та додамо константу для того, щоб отримати
, пiднесемо до квадрату та додамо константу для того, щоб отримати ![]() ; потiм повторимо розрахунки для того, щоб отримати
; потiм повторимо розрахунки для того, щоб отримати ![]() ,
, ![]() Ваi так далi.
Ваi так далi.
ВаПочнемо з найпростiшого iз можливих значень константи ![]() , тобто
, тобто ![]() . Тодi при кожнiй iтерацii пiдраховуiться точний квадрат числа:
. Тодi при кожнiй iтерацii пiдраховуiться точний квадрат числа: ![]() . У залежностi вiд значення розглядаiться три випадки:
. У залежностi вiд значення розглядаiться три випадки:
1. Якщо ![]() , тодi числа отримуються все меншi та меншi, iх послiдовнiсть прямуi до нуля.
, тодi числа отримуються все меншi та меншi, iх послiдовнiсть прямуi до нуля.
2. Якщо ![]() , тодi числа отримуються все бiльшi та бiльшi, прямуючи до нескiнченностi.
, тодi числа отримуються все бiльшi та бiльшi, прямуючи до нескiнченностi.
3. Якщо ![]() , тодi точки продовжують залишатися на вiдстанi 1 вiд нуля. РЗх послiдовностi лежать на границi двох областей тритягання, у данному випадку на колi (мал.18) з одиничним радiусом та центром у нулi.
, тодi точки продовжують залишатися на вiдстанi 1 вiд нуля. РЗх послiдовностi лежать на границi двох областей тритягання, у данному випадку на колi (мал.18) з одиничним радiусом та центром у нулi.

Мал.18
Ситуацiя така: площина дiлиться на двi зони впливу, а границя мiж ними i просто коло.
Сюрприз починаiться, коли ми вiзьмемо значення параметру ![]() Ване дорiвнюi нулю, наприклад
Ване дорiвнюi нулю, наприклад ![]() . У цьому випадку для послiдновностi присутнi також три вищеперелiчених випадкiв, але внутрiшня точка, до якоi прямуi послiдовнiсть, вже не i нулем, а границя вже не i плоскою, вона надто крива(мал.19). Саме це Б. Мандельброт назвав фрактальной структурой такоi границi.
. У цьому випадку для послiдновностi присутнi також три вищеперелiчених випадкiв, але внутрiшня точка, до якоi прямуi послiдовнiсть, вже не i нулем, а границя вже не i плоскою, вона надто крива(мал.19). Саме це Б. Мандельброт назвав фрактальной структурой такоi границi.

Мал.19
ВаОднiiю з таких характерних особливостей такоi границi i ii самоподiбнiсть. Якщо взяти будь-яку частину границi, то можна побачити, що вона зустрiчаiться в рiзних мiсцях границi та мають рiзнi розмiри. Границi такого виду в математицi називають множинами Жюлiа.
Рiзноманiтнi значення параметру ![]() Ваможуть створювати рiзноманiтнi множини Жюлiа, причому найменшi змiни цього параметру нерiдко призводять до суттiвих метаморфоз.
Ваможуть створювати рiзноманiтнi множини Жюлiа, причому найменшi змiни цього параметру нерiдко призводять до суттiвих метаморфоз.

Деякi множини Жюлiа звтАЩязнi, iншi являють собою ВлпилевиднiВ» канторовi множини(мал.20 а,б,в,г).
РЖснуi правило, що зтАЩясовуi вид множини Жюлiа. Воно залежить вiд параметру ![]() Вата повтАЩязано з зображенням множини Мандельброта. Множина всiх точок
Вата повтАЩязано з зображенням множини Мандельброта. Множина всiх точок ![]() , для яких iтерацii
, для яких iтерацii ![]() Вазалишаються обмеженими при
Вазалишаються обмеженими при ![]() , називаiться множиною Мандельброта (мал.21).
, називаiться множиною Мандельброта (мал.21).
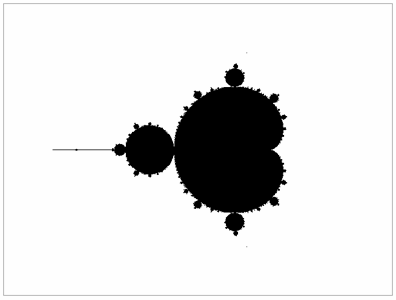
Мал.21
Цiкаво, що всi значення ![]() , при яких множини Жюлиа звтАЩязнi, належать множинi Мандельброта, тому останнi може бути визначеним i як множина всiх значень параметру
, при яких множини Жюлиа звтАЩязнi, належать множинi Мандельброта, тому останнi може бути визначеним i як множина всiх значень параметру ![]() , при яких множина Жюлiа звтАЩязна.
, при яких множина Жюлiа звтАЩязна.
![]()
![]() Сукупнiсть елементiв
Сукупнiсть елементiв ![]() Ваполя коплексних чисел, для яких послiдовнiсть:
Ваполя коплексних чисел, для яких послiдовнiсть: ![]() , що визначена iтерацiйно за правилом
, що визначена iтерацiйно за правилом ![]() , де тАжтАж задовольняi умову . Наприклад множина Мандельброта (мал.22 а,б,в,г,д,е).
, де тАжтАж задовольняi умову . Наприклад множина Мандельброта (мал.22 а,б,в,г,д,е).

а)![]() б)
б)![]() в)
в)![]()

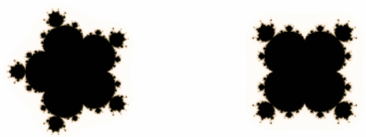
г) ![]() Вад)
Вад) ![]() Вае)
Вае) ![]()
Мал.22
Висновок
Фрактал i однiiю з багатьох складових частин певноi субстанцii, тому зникнення однiii з таких складових призводить до втрати вiзуальноi гармонii, що людське око розпiзнаi одразу. Присутнiсть фрактала з першого погляду можна i не помiтити, якщо не заглиблюватись у досконале вивчення математики. Ця наука, дiйсно, не маi меж i постiйно спонукаi до рiзноманiтних дослiджень.
Фрактал тАФ це математична величина, що зустрiчаiться досить часто. Але якщо добре не придивитися, його можна i не побачити. Абсолютно точна, алгебраiчна величина, яка творить собою неймовiрнi фiгури, вiзерунки та складаi цiкавi орнаменти, що ми зустрiчаiмо кожного дня. Це i листя папоротi, i маленькi снiжинки та ще багато iншого.
Галiлео Галiлей у 1623 роцi писав: тАЬВся наука записана у цiй великiй книзi, тАФ я маю на увазi Всесвiт, тАФ що завжди вiдкрита для нас, але яку неможливо зрозумiти, не навчившись розумiти мову, на якiй вона написана, а написана вона на мовi математики, i ii лутерами i трикутники, кола i iншi геометричнi фiгури, без яких людинi не можливо розiбрати жодного ii слова; без них вона подiбна блукаючому в пiтьмiтАжтАЭ
Поняття фрактала змiнило багато традицiйних уявлень про геометрiю, а в iсторii розвитку математики введення цього поняття стало переломним моментом. З кожним роком поняття фрактала стаi вiдоме все бiльш широкому колу людей. РЖ зараз цей термiн важко залишити без належноi уваги. У природi i багато чого, що маi прямий звтАЩязок до цього термiну.
Займаючись цiiю темою напротязi двох рокiв, я бiльш широко дiзнався про обтАЩiкт дослiдження: його властивостi, способи створення та використання. З алгебраiчних фракталiв я звернув увагу на три основнi iх види: множину Мандельброта, множину Жюлiа, дракон Хартера-Хейтуея, якi вiдрiзняються один вiд одного за побудовою та своiми загальними формулами створення, на мою думку, найбiльше дослiдженi в наш час. За допомогою iх зтАЩявляiться бiльшiсть новостворених фракталiв.
Знайшовши збiрник зображень фракталiв, що були створенi небагато рокiв тому, i серед яких провели конкурс на найкращий малюнок, мене дуже вразило розмаiття кольорiв та фантазiя людей. Менi стало вiдомо, яким чином вони створюються в наш час, що цiiю темою зацiкавленi люди, яким до вподоби неординарне художнi мистецтво, що не рiдко втiлюiться у комптАЩютернiй графiцi.
Сподiваюсь, що i пiсля закiнчення гiмназii, у мене залишиться велике бажання продовжити дослiджувати загальнi формули побудови фракталiв i за допомогою цих формул створювати новi фрактали та захоплюватися iхньою незрiвнянною красою.
Використана лiтература
1. Мандельброт Б. Фрактальная геометрия природы. тАФ М.: ВлИнститут компьютерных исследованийВ», 2002.
2. Пайтген Х.-О., Рихтер П. Х. Красота фракталов. тАФ М.: ВлМирВ», 1993.
3. Федер Е. Фракталы. тАФ М: ВлМирВ», 1991.
4. Фоменко А. Т. Наглядная геометрия и топология. тАФ М.: изд-во МГУ, 1993.
5. Фракталы в физике. Труды 6-го международного симпозиума по фракталам в физике, 1985. тАФ М.: ВлМирВ», 1988.
6. Шредер М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая. тАФ Ижевск: ВлРХДВ», 2001.
7. Мандельброт Бенуа, Ричард Л. Хадсон (Не)послушные рынки: фрактальная революция в финансах = The Misbehavior of Markets. тАФ М.: ВлВильямсВ», 2006. тАФ С. 400. ISBN 5-8459-0922-8
8. http://en.wikipedia.org/wiki/Fractal
9. http://en.wikipedia.org/wiki/Mandelbrot_set
10. http://en.wikipedia.org/wiki/Julia_set
Ва11. http://en.wikipedia.org/wiki/Newton_fractal
Ва12. http://en.wikipedia.org/wiki/Fractal_art
Ва13. http://commons.wikimedia.org/wiki/Fractal
Ва14.http://en.wikipedia.org/wiki/Fractal_landscape 15.http://" onclick="return false">
Ва16. http://" onclick="return false">
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
Автокорреляционная функция. Примеры расчётов