Применение тригонометрической подстановки для решения алгебраических задач
Решение задач является важнейшим видом учебной деятельности, в процессе которой учащимися усваивается математическая теория и развиваются логическое мышление и творческие способности. Развитие творческих способностей учащихся старших классов при обучении математике осуществляется более эффективно при вовлечении их в творческую деятельность, которая включает в себя:
1. Осознание, что данная конкретная задача есть представитель класса однородных задач.
2. Отыскание различных вариантов решения, их сопоставление, выявление сильных и слабых сторон каждого способа решения с целью выбора из них наиболее рационального, простого, ВлизящногоВ». Сравнение и анализ различных решений одной задачи делает знания более прочными и осознанными. Установлено, что решение одной и той же задачи несколькими способами приносит больше пользы, чем решение подряд такого же числа стереотипных заданий.
3. Самостоятельное комбинирование известных способов деятельности.
4. Изобретение, по крайней мере, для данной задачи принципиально нового приема решения.
Для развития творческих способностей учащихся наиболее ценными являются сложные и нестандартные задачи. Решение сложных задач по математике во многом зависит от опыта их решения, от степени овладения методами их решения и техникой преобразований. Нестандартные задачи тАУ это задачи, для решения которых у учащихся нет готового алгоритма и нужен самостоятельный поиск ключевой идеи. При решении нестандартных задач формируется математическая культура, воспитывается гибкость ума и осуществляется постижение единства математики. Вот почему, по мнению Д. Пойа, Влнестандартные задачи могут способствовать интеллектуальному развитию ученика, чего нельзя сказать о стандартныхВ» [36].
Важнейшим источником нестандартных задач являются олимпиадные и конкурсные задания. Как правило, нестандартные задачи требуют нестандартного подхода к их решению. Важно, чтобы у учащихся был создан запас методов решения нестандартных задач, так как не всегда школьники могут самостоятельно додуматься до нестандартного метода решения.
С точки зрения стандартных школьных методов решения алгебраических задач метод тригонометрической подстановки является нестандартным приемом. С другой стороны, тригонометрическая подстановка позволяет решать сложные многоходовые задачи. Она применяется при решении таких алгебраических задач, которые своими средствами не решаются или решаются очень сложно.
Учащиеся классов с углубленным изучением математики знакомятся с методом тригонометрической подстановки [21], [57] но есть смысл в более подробном и глубоком его изучении. Необходимость в таком изучении в классах с углубленным изучением математики обусловлена следующими положениями.
1. Углубленное изучение предполагает наполнение курса разнообразными, интересными и нестандартными задачами, которые играют существенную роль в развитии творческих способностей учащихся. Применение тригонометрической подстановки для решения задач позволяет дать эффективный способ решения нестандартных олимпиадных задач [8], [9], [16], [25], [29].
2. Учащиеся классов с углубленным изучением математики в условиях серьезного конкурса на вступительных экзаменах в вузы с профилирующим изучением математики окажутся перед необходимостью решить трудные и очень трудные задачи. Неоценимую помощь в таком решении им может оказать метод тригонометрической подстановки [4], [10], [30], [31], [37]-[40], [44], [51], [52].
3. Задачи, предлагаемые к решению с помощью тригонометрической подстановки, базируются на достаточно высоком уровне владения техникой как алгебраических, так и тригонометрических преобразований. Это позволяет оценить метод решения и применить его в сходной ситуации.
4. Применение тригонометрической подстановки приучает учащихся к полноте аргументации введения подстановки для решения задач.
5. Применение тригонометрической подстановки при решении алгебраических задач направлено на установление взаимосвязи различных разделов математики, а именно: алгебры и тригонометрии. Важно воспитать у учащихся смелости и находчивости в поиске способов решения задач не только в ближайшем окружении условия, но и в более широкой, иногда неожиданной области.
Наиболее уместно организовать работу, посвященную применению тригонометрической подстановки для решения алгебраических задач, на факультативных занятиях по математике. При этом целесообразно предложить учащимся для решения разнообразные задачи: рациональные и иррациональные уравнения, неравенства, их системы, задания на отыскание наибольшего и наименьшего значений функции, задачи с параметрами. Желательно создать такую работу, которая бы содержала в себе подборку из разнообразных алгебраических заданий, решаемых с помощью тригонометрической подстановки, не ограничиваясь рассмотрением отдельного класса задач.
Цель работы: разработать методику применения тригонометрической подстановки для решения алгебраических задач старшими школьниками на факультативных занятиях в классах с углубленным изучением математики.
Объект исследования: процесс применения тригонометрической подстановки как метода решения разнообразных алгебраических задач.
Предмет исследования: организация деятельности учащихся по овладению тригонометрической подстановки на факультативных занятиях в классах с углубленным изучением математики.
При исследовании исходим из гипотезы, что применение методики, разработанной на основе сравнительного анализа решения большого числа задач, позволит развить творческие способности учащихся и подготовит их к вступительным экзаменам в серьезные вузы.
Для достижения поставленной цели и проверки гипотезы необходимо решить следующие задачи:
1. Выявить теоретические основы возможности введения тригонометрической подстановки.
2. Провести сравнительный анализ решения задач с помощью тригонометрической подстановки и без нее.
3. На основе проведенного сравнительного анализа разработать методику изучения тригонометрической подстановки при решении алгебраических задач на факультативных занятиях по математике в старших классах с углубленным изучением математики.
4. Провести опытное испытание эффективности разработанной методики.
Глава 1
Метод замены переменной при решении задач
Вз1. Общие положения
Переход к новым обозначениям, замена неизвестных тАУВа существенный прием и метод, который применяется при решении самых различных задач как элементарной, так и высшей математики. Очень важно, чтобы этот прием и метод был прочно усвоен и освоен в школе, так как идея замены переменной является сквозной и в том или ином виде фигурирует практически во всех разделах школьной математики.
Существуют два подхода к определению метода замены переменной. Если уравнение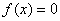 
Ваудалось преобразовать к виду 
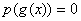, то нужно ввести новую переменную 
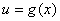, решить уравнение 
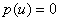, а затем рассмотреть совокупность уравнений
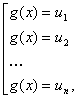
где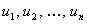 
тАУ корни уравнения 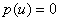. Чтобы при замене не потерять корней, достаточно убедиться, что каждому значению 
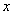Ваиз рассматриваемой области соответствует хотя бы одно значение 
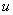, удовлетворяющее равенству .
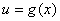В отличие от описанного выше метод равносильной замены требует нахождения множества значений переменной 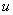. В данном случае накладывается требование: каждому значению 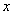Ваиз рассматриваемой области соответствует ровно одно значение переменной 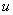, удовлетворяющее равенству 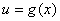. Такой подход ведет к сохранению области определения исходного уравнения и не требует перехода к совокупности.
Подобные замены порой существенно упрощают решение. Замена переменных и переход к новым обозначениям облегчают выкладки и делают громоздкое алгебраическое выражение компактным и обозримым. Вот почему следует приучать школьников при решении задач не торопиться начинать преобразования: пусть они сначала посмотрят, нельзя ли записать уравнение проще, введя новую переменную. При этом не стоит забывать, что, во-первых, далеко не всегда замена бывает столь уж необходима. Во-вторых, если приходится прибегать к замене неизвестной, то стоит сразу подобрать ее так, чтобы она вбирала в себя по возможности большее количество неприятных деталей, затрудняющих решение.
Умение удачно ввести новую переменную тАУ важнейший элемент математической культуры школьника. При этом искусство производить замену переменных заключается в том, чтобы увидеть, какая замена будет более рациональна и быстрее приведет к успеху.
Новая переменная иногда очевидна, иногда несколько завуалирована, но ВлощущаетсяВ». В более сложных случаях, для того чтобы найти удачную замену неизвестной, требуется дополнительная творческая работа, которая впоследствии окупается простотой и изящностью решения.
Учить методу замены, выбору удачных новых переменных следует специально еще и потому, что не всегда учащиеся могут додуматься до него самостоятельно. В таких случаях удобную подстановку желательно знать заранее. Особенно трудно учащимся представить себе, что вместо переменной можно подставить тригонометрическую функцию, поскольку при этом, как кажется, алгебраическое выражение усложняется. Однако известные свойства тригонометрических функций упрощают некоторые уравнения, неравенства и их системы, в то время как прямое алгебраическое решение оказывается более сложным технически. Таким образом, тригонометрическую подстановку можно назвать нестандартным методом решения стандартных по постановке задач тАУ уравнений, неравенств и их систем.
Вз2. Тригонометрическая подстановка
Тригонометрическая подстановка является одним из способов реализации метода замены переменной и используется в тех случаях, когда область определения исходного уравнения совпадает с областью значения тригонометрической функции или включается в эту область. Выбор той или иной функции при этом зависит от вида уравнения, неравенства, их систем или алгебраического выражения, которое требуется упростить.
Если из условия задачи следует, что допустимые значения переменной 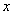Ваопределяются неравенством 
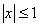, то удобны замены 
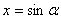Ваили 
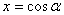. В первом случае достаточно рассмотреть 
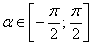, так как на этом промежутке непрерывная функция 
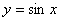Вавозрастает, поэтому каждое свое значение принимает ровно в одной точке. Непрерывная функция 
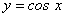Ваубывает на промежутке 
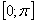, поэтому также каждое свое значение принимает ровно в одной точке. Вот почему в случае замены 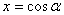, достаточно взять 
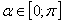. Причем какую из двух подстановок выбрать, зависит от конкретной ситуации.
В случаях, когда переменная может принимать любые действительные значения, используются замены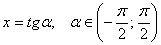 
Ваили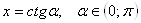 
, так как область значения функции 
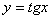Ваи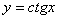 
Вана соответствующих промежутках есть множество всех действительных чисел.
Реже используются замены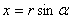 
Ваили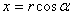 
, где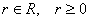 
, а выбор значений 
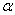Васнова зависит от конкретной ситуации.
Когда выражение зависит от двух переменных 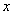Ваи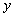 
, целесообразно положить , 
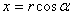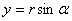, где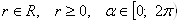 
. Такая замена законна. Действительно, для любых 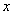Ваи 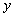Васуществует такое 
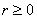, что 
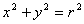. При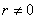 
Ваимеем 
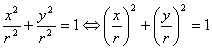. А числа, сумма квадратов которых равна единице, по модулю не превосходят единицы и их можно рассматривать как синус и косинус некоторого угла. Геометрический смысл такой замены состоит в следующем: для каждой точки 
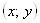Ваопределяется расстояние 
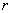Вадо начала координат и угол 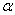Ванаклона вектора 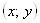Вак положительному направлению оси абсцисс.
И последнее замечание. Реализовать такую подстановку не так уж трудно, главное и, наверное, самое сложное тАУ суметь ее увидеть. Поэтому целесообразно помочь учащимся научиться распознавать ВлприметыВ» тригонометрических подстановок. Содержание следующей главы направлено на выработку соответствующих умений.
Глава 2
ПРИМЕНЕНИЕ МЕТОДА
ТРИГОНОМЕТРИЧЕСКОЙ ПОДСТАНОВКИ ПРИ РЕШЕНИИ ЗАДАЧ
Вз1. Решение уравнений
1.1 ВаИррациональные уравнения
ВаВаВаВа Иррациональные уравнения часто встречаются на вступительных экзаменах по математике, так как с их помощью легко диагностируется знание таких понятий, как равносильные преобразования, область определения и другие. Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. Эквивалентность не нарушается при возведении обеих частей в нечетную степень. В противном случае требуется проверка найденных решений или оценка знака обеих частей уравнения. Но существуют и другие приемы, которые могут оказаться более эффективными при решении иррациональных уравнений. Например, метод тригонометрической подстановки.
Пример 1. ВаРешите уравнение
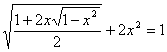Ва[12].
Решение с помощью тригонометрической подстановки
Так как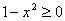 
, то 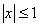. Поэтому можно положить 
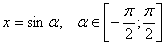. Уравнение примет вид
.
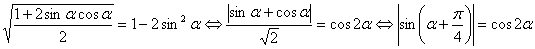Положим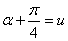 
, где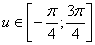 
, тогда
.
.
.
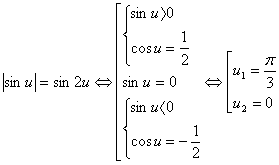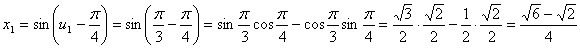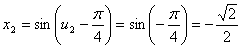Ответ: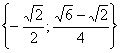 
.
Алгебраическое решение
.
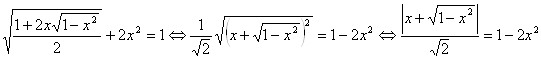Так как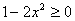 
, то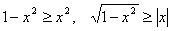 
. Значит, 
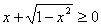, поэтому можно раскрыть модуль
.
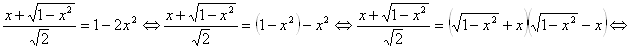
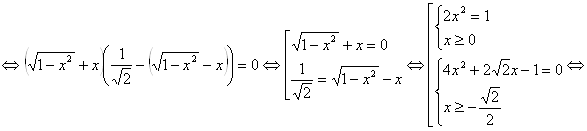
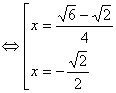Ответ: .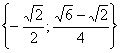
Решение уравнения алгебраическим способом требует хорошего навыка проведения тождественных преобразований и грамотного обращения с равносильными переходами. Но в общем оба приема решения равноценны.
Пример 2. Решите уравнение
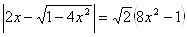Ва[14].
Решение с помощью тригонометрической подстановки
Область определения уравнения задается неравенством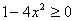 
, что равносильно условию 
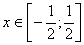, тогда 
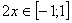. Поэтому можно положить 
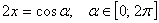. Уравнение примет вид
.
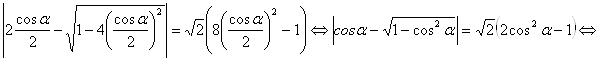
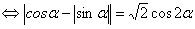Так как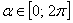 
, то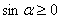 
. Раскроем внутренний модуль
.
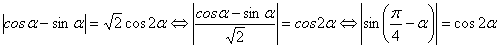Положим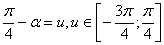 
, тогда
.
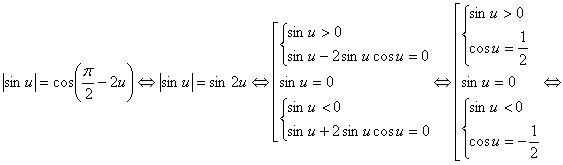
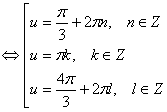Условию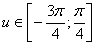 
Ваудовлетворяют два значения Ва
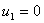Ваи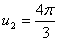 
.
.
.
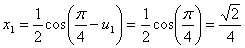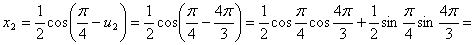
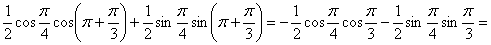
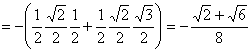Ответ: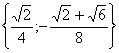 
.
Алгебраическое решение
.
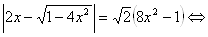
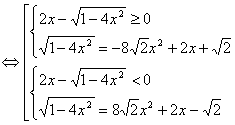Возведем в квадрат уравнение первой системы совокупности, получим
.
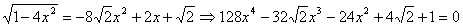Пусть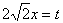 
, тогда 
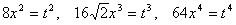. Уравнение перепишется в виде
.
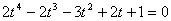Проверкой устанавливаем, что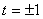 
ВатАУ корень, тогда делением многочлена 
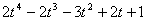Вана двучлен 
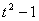получаем разложение правой части уравнения на множители
.
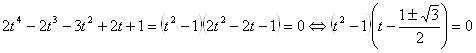От переменной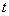 
Ваперейдем к переменной 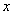, получим
.
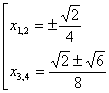Условию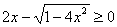 
Ваудовлетворяют два значения
.
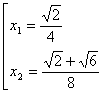Подставив эти значения в исходное уравнение, получаем, что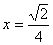 
ВатАУ корень.
Решая аналогично уравнение второй системы исходной совокупности, находим, что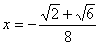 
Ватоже корень.
Ответ: .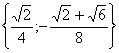
Если в предыдущем примере алгебраическое решение и решение с помощью тригонометрической подстановки были равноценны, то в данном случае решение подстановкой выгоднее. При решении уравнения средствами алгебры приходится решать совокупность из двух уравнений, то есть дважды возводить в квадрат. После этого неравносильного преобразования получаются два уравнения четвертой степени с иррациональными коэффициентами, избавиться от которых помогает замена. Еще одна трудность тАУ проверка найденных решений подстановкой в исходное уравнение.
Пример 3. Решите уравнение
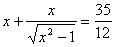Ва[31].
Решение с помощью тригонометрической подстановки
Так как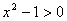 
, то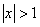 
. Заметим, что отрицательное значение неизвестного не может быть решением задачи. Действительно, преобразуем исходное уравнение к виду
.
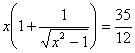Множитель в скобках в левой части уравнения положительный, правая часть уравнения тоже положительная, поэтому множитель 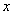Вав левой части уравнения не может быть отрицательным. Вот почему 
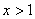, тогда 
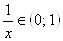, поэтому можно положить 
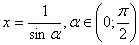ВаИсходное уравнение перепишется в виде
.
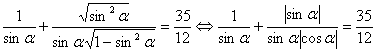Так как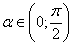 
, то 
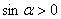Ваи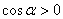 
. Уравнение примет вид
.
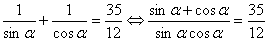Пусть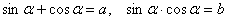 
. Перейдем от уравнения к равносильной системе
.
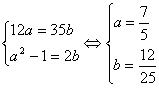Числа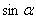 
Ваи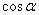 
Ваявляются корнями квадратного уравнения
.
.
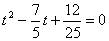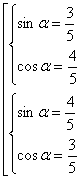Ответ: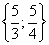 
.
Алгебраическое решение
Возведем обе части уравнения в квадрат
.
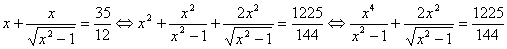Введем замену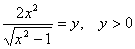 
, тогда уравнение запишется в виде
.
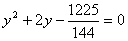
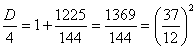
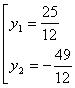Второй корень является лишним, поэтому рассмотрим уравнение
.
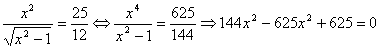
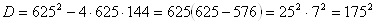
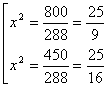Так как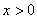 
, то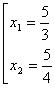 
.
Ответ: .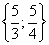
В данном случае алгебраическое решение в техническом плане проще, но рассмотреть приведенное решение с помощью тригонометрической подстановки следует обязательно. Это связано, во-первых, с нестандартностью самой подстановки, которая разрушает стереотип, что применение тригонометрической подстановки возможно лишь, когда 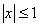. Оказывается, если 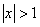Ватригонометрическая подстановка тоже находит применение. Во-вторых, представляет определенную трудность решение тригонометрического уравнения 
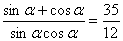, которое сводится введением замены к системе уравнений. В определенном смысле эту замену тоже можно считать нестандартной, а знакомство с ней позволяет обогатить арсенал приемов и методов решения тригонометрических уравнений.
Пример 4. Решить уравнение
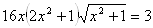Ва[4].
Решение с помощью тригонометрической подстановки
Так как переменная 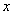Ваможет принимать любые действительные значения, положим 
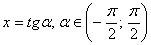. Тогда
,
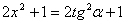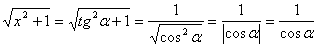,так как 
.
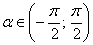Исходное уравнение с учетом проведенных преобразований примет вид
.
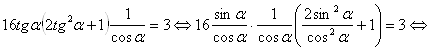
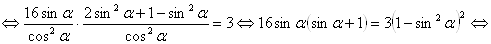
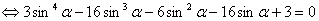Так как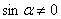 
, поделим обе части уравнения на 
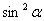, получим
.
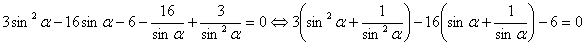Пусть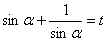 
, тогда 
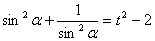. Уравнение примет вид
.
.
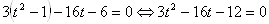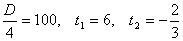Учитывая подстановку 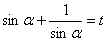, получим совокупность из двух уравнений
.
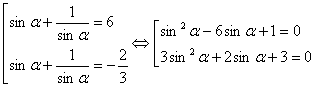Решим каждое уравнение совокупности по отдельности.
1)ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа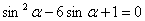 
.
.
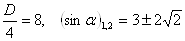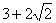Ване может быть значением синуса, так как 
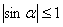Вадля любых значений аргумента.
.
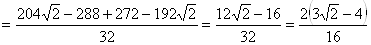Откуда
.
Так как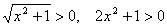 
Ваи правая часть исходного уравнения положительна, то 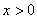. Из чего следует, что 
.
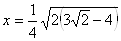2)ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа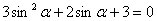 
.
.
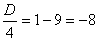Это уравнение корней не имеет, так как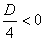 
.
Итак, исходное уравнение имеет единственный корень
.
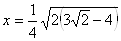Ответ: 
.
Алгебраическое решение
Данное уравнение легко ВлпревратитьВ» в рациональное уравнение восьмой степени возведением обеих частей исходного уравнения в квадрат. Поиск корней получившегося рационального уравнения затруднен, и необходимо обладать высокой степенью изобретательности, чтобы справиться с задачей. Поэтому целесообразно знать иной способ решения, менее традиционный. Например, подстановку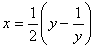 
, предложенную И. Ф. Шарыгиным [57].
Положим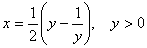 
, тогда
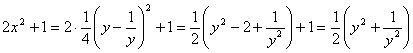
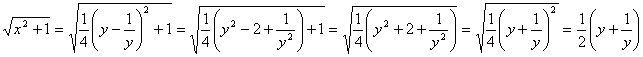Преобразуем правую часть уравнения :
.
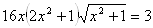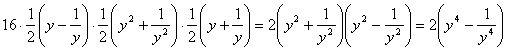С учетом преобразований уравнение 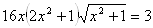Вапримет вид
.
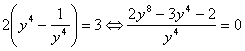Введем замену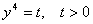 
, тогда
.
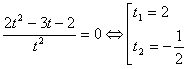Второй корень является лишним, поэтому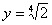 
, а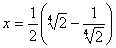 
.
Ответ: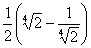 
.
Если заранее не известна идея решения уравнения 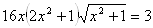, то решать стандартно возведением обеих частей уравнения в квадрат проблематично, так как в результате получается уравнение восьмой степени 
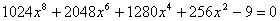, найти корни которого чрезвычайно сложно. Решение с помощью тригонометрической подстановки выглядит громоздким. Могут возникнуть трудности с поиском корней уравнения 
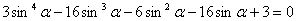, если не заметить, что оно является возвратным. Решение указанного уравнения происходит с применением аппарата алгебры, поэтому можно сказать, что предложенное решение является комбинированным. В нем сведения из алгебры и тригонометрии работают совместно на одну цель тАУ получить решение. Также решение указанного уравнения требует аккуратного рассмотрения двух случаев. Решение заменой 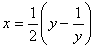технически проще и красивее, чем с помощью тригонометрической подстановки. Желательно, чтобы учащиеся знали такой способ замены и применяли его для решения задач.
Подчеркнем, что применение тригонометрической подстановки для решения задач должно быть осознанным и оправданным. Использовать подстановку целесообразно в тех случаях, когда решение другим способом сложнее или вовсе невозможно. Приведем еще один пример,Ва который, в отличие от предыдущего, проще и быстрее решается стандартным способом.
Пример 5. Решить уравнение
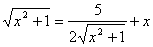Ва[51].
Решение с помощью тригонометрической подстановки
Так как переменная 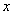Ваможет принимать любые действительные значения, можно положить 
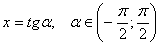. Уравнение примет вид
.
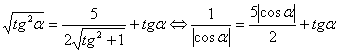В силу того, что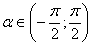 
, можно раскрыть модуль
.
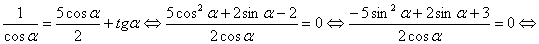
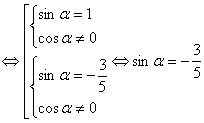Так как 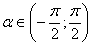, то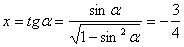 
.
Ответ: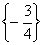 
.
Алгебраическое решение
Проверкой убеждаемся, что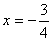 
ВатАУ корень.
Ответ: .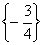
1.2 Рациональные уравнения
Тригонометрическая подстановка применяется при решении рациональных уравнений, когда уравнение не имеет рациональных корней или найденные рациональные решения не исчерпывают всего множества решений уравнения.
При решении иррациональных уравнений возможность введения тригонометрической подстановки была видна по структуре уравнения. В нескольких следующих задачах применение метода тригонометрической подстановки не так очевидно. Вот почему прежде чем ввести подстановку, нужно доказать законность такого введения.
Пример 1. Сколько корней имеет уравнение
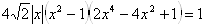Ва[37].
Решение этой задачи любым методом начинается одинаково. Докажем, что все корни данного уравнения принадлежат промежутку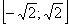 
. Действительно, если
.
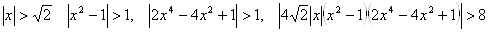Но тогда в исходном уравнении слева стоит произведение больше восьми, а справа единица, что невозможно.
Решение с помощью тригонометрической подстановки
Положим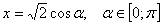 
. Тогда каждому корню 
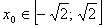Ваисходного уравнения будет соответствовать ровно один корень 
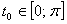, где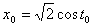 
. Наоборот, каждому корню 
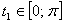Вауравнения соответствует ровно один корень исходного уравнения. Таким образом, задача может быть переформулирована так: сколько корней на промежутке 
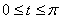Ваимеет уравнение
.
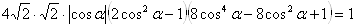Так как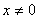 
Ваи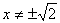 
, то можно взять 
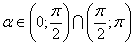. Заметим, что если 
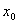Ва- корень данного уравнения, то и 
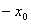Ватоже корень. Вот почему достаточно рассмотреть 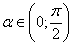, то есть отыскать только положительные решения. С учетом выше изложенного исходное уравнение перепишется в виде
.
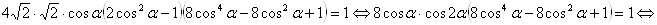
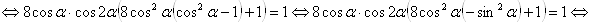
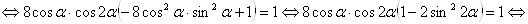
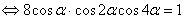Так как 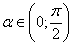, то можно обе части равенства умножить на 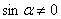, получим
.
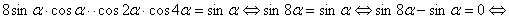
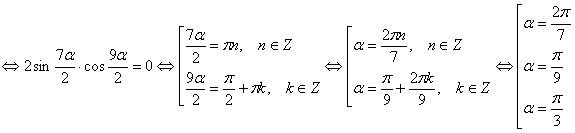Ответ: шесть корней.
Алгебраическое решение
Так как выражение от правой части равенства четное 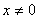и Ваи 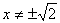, выясним вопрос о наличии корней на промежутке 
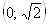. Проверкой устанавливаем, что 
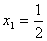ВатАУ корень. Рассмотрим функции от правой и левой частей уравнения, то есть функции 
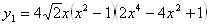Ваи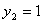 
. Так как
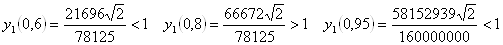
и функцияВа 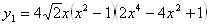Ванепрерывна на числовой прямой, то найдутся такие значения 
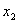Ваи 
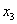, что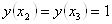 
. Поэтому на промежутке 
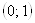Вауравнение имеет три корня, а на всей числовой прямой тАУ шесть корней.
Ответ: 6 корней.
В данном случае можно решать любым способом, но если количество корней на небольшом промежутке достаточно велико, вычисления могут оказаться громоздкими, и сам метод неэффективным. В этом случае на помощь приходит метод тригонометрической подстановки. Надо заметить, что решить вопрос о количестве корней можно с помощью производной, но в данном случае такое решение мало эффективно, так как затруднительно найти нули производной.
Пример 2. Решить уравнение
.
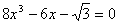Если для выше приведенных задач не удается найти нетрадиционный путь решения, то все равно остается вероятность справиться с задачей с помощью стандартных школьных рассуждений, правда, затратив при этом гораздо больше времени. Эта задача лишает такого выбора, так как ее решение другим способом не представляется возможным.
Решение с помощью тригонометрической подстановки
Поделим все члены уравнения на 2. Уравнение примет вид
.
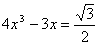Докажем, что все корни данного уравнения по модулю не превосходят единицы. Пусть 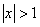, тогда 
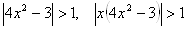. Получили, что при 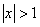Валевая часть уравнения по модулю больше единицы, а правая тАУ меньше единицы, что невозможно.
Положим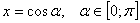 
. Уравнение примет вид
.
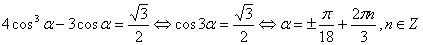Условию 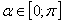Ваудовлетворяют три значения
.
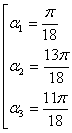Поскольку кубическое уравнение не может иметь больше трех различных корней, то мы нашли все решения.
Ответ: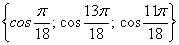 
.
ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 1.3 Показательные уравнения
Приведем пример задания, решить которое без введения тригонометрической подстановки не представляется возможным.
Пример 1. Решить уравнение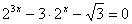 
.
Пусть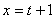 
, тогда уравнение перепишется в виде
.
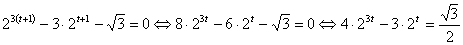Введем замену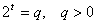 
, получим
.
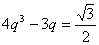Это уравнение мы уже решали[1]
. Его корни
.
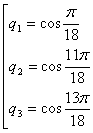Два последних значения меньше нуля, поэтому нам подходит только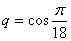 
. Перейдем к переменной 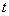, а затем к переменной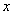
.
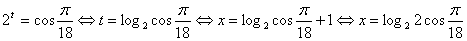Ответ: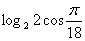 
.
Вз2. Решение систем
В данном параграфе предложены системы повышенной сложности, решить которые, не зная специальных методов решения, сложно.
Пример 1. Решить систему уравнений
Ва[3].
Решение с помощью тригонометрической подстановки
Так как квадрат суммы чисел 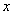Ваи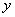 
равен единице, то каждое из этих чисел по модулю не превосходит единицы и их можно рассматривать как синус и косинус некоторого угла. Поэтому можно положить 
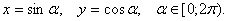ВаВторое уравнение системы примет вид
.
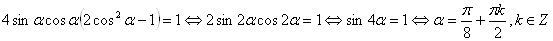Условию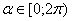 
Ваудовлетворяют четыре значения
.
.
.
.
.
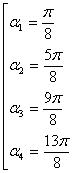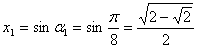
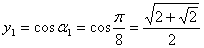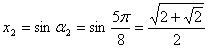
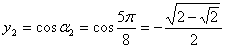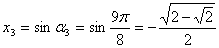
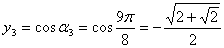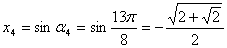
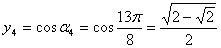Ответ: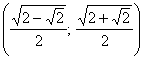 
; 
; 
; 
.
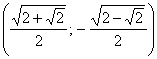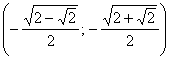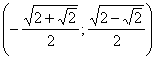Алгебраическое решение
.
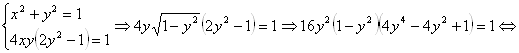
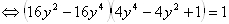Пусть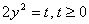 
, тогда 
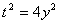. Имеем
.
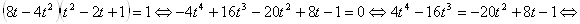
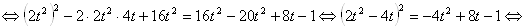
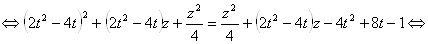
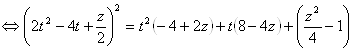Подберем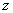 
Ватак, чтобы многочлен, стоящий в правой части равенства, стал полным квадратом. Для этого он должен иметь один двукратный корень, то есть
.
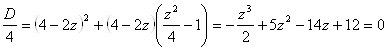Подбором находим, что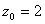 
Ваявляется корнем уравнения
.
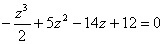Подставим 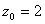Вав уравнение 
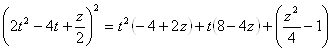, после чего оно примет вид
.
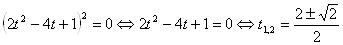Перейдем к переменной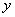
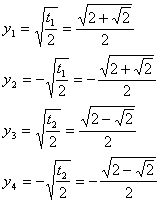
Подставив получившиеся значения переменной 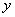Ваво второе уравнение системы, найдем соответствующие значения переменной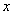
Ответ: ; ; ; .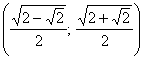
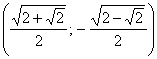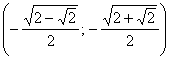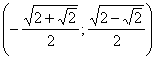Пример 2. Сколько решений имеет система уравнений
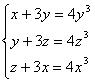[18].
Здесь представлена так называемая циклическая система уравнений. Подобные системы часто предлагаются на вступительных экзаменах в вузы с повышенными требованиями по математике [30]. Решить эти системы, не зная специальных методов решения, очень сложно. В данном случае подбором устанавливается решение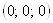 
. Попытки доказать, что система не имеет других решений, положительных результатов не дают. Неоценимую помощь в решении такого класса задач оказывает метод тригонометрической подстановки.
Перепишем систему в виде
.
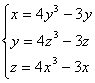Докажем, что все числа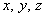 
Вапо абсолютной величине не превосходят единицы. Пусть ![]()
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
РЖнтегральнi характеристики векторних полiв
РЖнтерполювання функцiй
Автокорреляционная функция. Примеры расчётов
Аксонометричнi проекцii