Методичний матерiал по викладанню алгебри

ЗМРЖСТ

Урок тАУ 1. Поняття про вектори. Абсолютна величина вектора i напрям

Урок тАУ 2. Рiвнiсть векторiв. РозвтАЩязування вправ

Урок тАУ 3. Координати вектора

Урок тАУ 4. РозвтАЩязування вправ. Самостiйна робота

Урок тАУ 5. Додавання векторiв

Урок тАУ 6. Додавання векторiв (продовження)

Урок тАУ 7. Додавання векторiв (продовження)

Список використаноi лiтератури

УРОК тАУ 1 Тема уроку. ПОНЯТТЯ ПРО ВЕКТОР. АБСОЛЮТНА ВЕЛИЧИНА ВЕКТОРА РЖ НАПРЯМ

Мета уроку. Увести поняття вектора, абсолютна величина й напрям вектора, а також розвтАЩязати вправи.

Тип уроку. Урок засвоiння нових знань.

Навчальнi посiбники i ТЗН. 1)кодоскоп; 2)кодопозитиви; 2)дiапроек- тор; 4) фрагменти з дiафiльму тАЭ Вектор тАЭ.

ХРЖД УРОКУ

РЖ. Повторення вивченого матерiалу(фронтальне опитування накодоскопi).

1). Якi вiдображення площини на себе називаiться рухом (перемi- щенням)? Перерахувати вiдомi вам види перемiщення.

[симетрiя вiдносно точки, симетрiя вiдносно прямоi, поворот, паралельне перенесення].

2). Дати означення напряму на площинi.

[Наочно паралельне перенесення означають як перетворення, при якому точки змiщуються в одному i тому самому напряму на одну i ту саму вiдстань, або точки змiщуються вздовж паралельних прямих ( або прямих якi збiгаються) на одну й ту саму вiдстань].

3). Яке вiдображення площини на себе називаiться паралельним пере- несенням?

4). Яке вiдображення площини на себе називаiться паралельним пере- несенням?

[Паралельне перенесення задаiться формулами:

x'=x+a, y'=y+b ].

5). Скiльки рiзних паралельних перенесень задають двi рiзнi точки? [A(x₁;y₁), B(x₂;y₂) переходять при паралельному перенесеннi у точки A'(x₁+a;y₁+b), B'(x₂+a;y₂+b)].

РозвтАЩязати задачу на тотожне вiдображення.

Дано вiдрiзок AB. Побудувати образ цього вiдрiзка

а) При паралельному перенесеннi, який переводить точку A у точку В.

AB].ВаВаВаВаВа [AB AB].

б) При поворотi на 0^o навколо вибраноi поза вiдрiзком AB точки. [AB

в) Чи являiться довiльне перемiщення тотожнiм вiдображенням, якщо вiдомо,що воно переводить точку А в точку В, а також В в точку В, тобто АВ АВ? [Нi, бо при будь-якому розмiщеннi осi симетрii з вiссю AB на площинi знайдуться точки, якi не переходять самi в себе, а тотожне вiдображення i перетворення всiii площини на себе, яка будь-яку точку площини вiдображаi на себе].

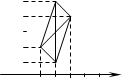
Паралельне перенесення задано формулами x=x+2, y=y+3. Знайдiть координати точок N' i M', в якi переходять точки N(1;2), M(2;1) при паралельному перенесеннi. Побудувати точки N i N ', M i M'; кожну пару точок зтАЩiднайте вiдрiзком.

Демонструю на кодоскопу мал. 1, який складаiться з кодоплiвок: система координат, iз двох пар точок N i N', M i M'. Одержаний малюнок показуi, що при даному паралельному перенесеннi точки змiстилися за паралельними прямими на однакову вiдстань. Пропоную учням цю властивiсть довести, тобто, що чотирикутник NN'M'M тАУ паралелограм. Для доведення вправи необхiдно згадати з учнями означення й властивiсть паралелограма, формули координат середини вiдрiзка.

Пропоную учням знайти середину вiдрiзка NM' i N'M i переконатися, що цi точки спiвпадають. Учнi роблять висновок, що дiагоналi чотирикутника NN'M'M перетинаються i в точцi перетину дiляться навпiл, це означаi, що NN'M'M тАУ паралелограм. Таким чином доведено, точки N i M змiстили на одну i ту ж вiдстань.

Потiм я доводжу це твердження в загальному виглядi ( тобто для будь-якого паралельного перенесення i довiльних точок N i M ), показую на кодоскопi мал. 1.

Алгоритм доведення демонструю на кодоскопi.

Нехай O₁ тАУ середина вiдрiзка NM', а O₂ тАУ середина вiдрiзка N'M. Знайти координати точок i.

Для O₁:

x = (x₁+x₂+a)/2, y = (y₁+ y₂ b)/2;

для O₂ :

x = (x₁+a+x₂)/2, y = (y₁ +y₂+b)/2.

Точки О₁=О₂ тАУ спiвпадають (одна i та ж точка).

Отже, дiагональ чотирикутника N'NM'M перетинаються i точкою перетину i точка О (середина ); звiдки слiдуi, що чотирикутник NN'M'M тАУ паралелограм (мал. 2), тобто NN' || MM' i NN'=MM'.

y

N(x₁+a;y₁+b)

5

M(x₂+a;y₂+b)

o

2 N

MВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 0 1 2 3 4 x

Мал. 2

Звертаю увагу учням на те, що ми довели наступне:

а) NM=N'M', тобто, що паралельне перенесення зберiгаi вiдстань мiж точками, а це означаi тАУ рух;

б) пряма переходить у паралельну пряму.

Пригадати з учнями теорему 9.4 (про iснування i iдиностi паралельного перенесення).

Пiдвести пiдсумок фронтального опитування й оголосити оцiнки.

РЖРЖ. Вивчення нового матерiалу.

Звертаю увагу учням на те, що ми повторили паралельне перенесення, яке тепер буде називатися по новому тАУ вектор.

Пiсля таких мiркувань переходимо до означення вектора, яке подано у пiдручнику (п. 91).

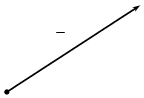
Вектором називаiться напрямлений вiдрiзок (за пiдручником мал. 215 демонструю на кодоскопу).

ВаB

Ваa

ВаA

мал. 3 (за пiдручником мал. 211)

Звертаю увагу на те, що учнi вже зустрiчалися iз вектором у курсi фiзики при вивченнi величин, якi характеризуються числом i напрямом (такi, як сила, швидкiсть i т. д.).

На мал. 3 напрям вектора визначаiться його початком i кiнцем (стрiлка). Для позначення вектора використовуються малi букви латинського алфавiту a, b, c

Можна також позначати вектор, вказавши його початок i кiнець великими буквами латинського алфавiту. При такому способi позначення

вектора на перше мiсце ставлять його початок (перша буква), а кiнцем i друга буква. Зверху над буквою (буквами) ставлять риску (стрiлку). Повiдомляю, що вектор на мал. 3 позначають так: a i AB.

ВаB C

A D

Мал. 4

На кодоскопу демонструю наступнi завдання:

1. Виписати всi вектори, зображенi на мал. 4.

2. Дано точки A,B,C,D (мал. 5):

а) зобразити вектори, DA, BA,DB,BC;

B

C

A D

Мал. 5

б) накреслити вектор, початок якого спiвпадаi iз

початком вектора DB, а кiнець тАУ з кiнцем вектора DC.

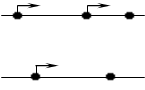
Пiсля розвтАЩязування цих вправ увожу поняття однаково напрямлених векторiв. Показую на кодоскопу мал. 6 i пояснюю учням, яке паралельне перенесення сумiщаiться, а) пiв прямi AB i DE; б) пiв прямi AB i BC.

A B C

D E

Мал. 6

[а) паралельне перенесення, переводить точку в точку A у точку B; б) паралельне перенесення, переводить точку А в точку В ].

Звертаю увагу учням на те, що згiдно означенню однаково напрямленнi пiв прямi лежать або на паралельних прямих, або на однiй i тiй же прямiй.

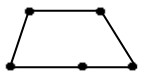B C

A N D

Мал. 7

На кодоскопу демонструю мал. 7 i умову завдання:тАЭ ABCD тАУ трапецiя. Пояснити, чому пiв прямi BC i AD однаково напрямленi тАЭ [Пiв прямi BC i AD лежать на паралельних прямих ВС i AD по одну сторону вiд сiчноi AB].

Увожу означення протилежно напрямленнi пiв прямi. Демонструю мал. 8 на кодоскопу.

Пояснити, чому пiв прямi BC i DA протилежно напрямленi.[Пiв прямi BC i DA лежать на паралельних прямих по одну сторону вiд сiчноi AB ].

Звертаю увагу на те, що протилежно напрямленнi пiв прямi (подiбно до однаково напрямлених ) лежать або на паралельних прямих, або на однiй й тiй же прямiй.

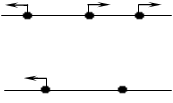
ВаK M N

F E

Мал. 8

Означення однаково напрямлених векторiв показую на прикладах. За допомогою кодоскопу демонструю мал. 7 i умову завдання.

Дано трапецiю ABCD (мал. 7):

а) Знайти всi можливi пари одинаково напрямлених векторiв.

б) Чи являються ВА CD однаково напрямленнi? (Вiдповiдь пояснiть)

Ввожу поняття протилежно ( ) напрямленнi вектори :тАЭCB i AD (мал. 7) називаються протилежно напрямленими, якщо пiв прямi CB i AD протилежно напрямленiтАЭ. Пiсля цього демонструю задаю ще одне запитання:

тАЭВкажiть якi-небудь пари протилежно напрямлених векторiвтАЭ.

[Наприклад, BC i DA, AD i NA, BC i CB].

Пiдсумок. Вектори CB AD називаються однаково напрямленими, якщо однаково напрямленi й пiв прямi CB i AD. Вектори CB AD називаються протилежно напрямленими, якщо протилежно напрямленi й пiв прямi CB i AD.

Для введення поняття абсолютноi величини (модуля) пропоную учням такi вправи.

Нехай ABCD тАУ квадрат iз стороною рiвною 3.

Чому дорiвнюють абсолютнi величини (модулi) векторiв AB, BA, AC ?

Пiдсумовую разом з учнями: тАЭ Абсолютною (або модулем) вектора називаiться довжина вiдрiзка, що зображаi вектор. Абсолютна величина вектора а позначаiться | a | тАЭ.

Далi знайомлю учнiв iз нульовим вектором, тобто, коли початок вектора збiгаiться з кiнцем. Показую як позначаiться нульовий вектор i учнi записують це позначення в зошитi ( 0 ). А також зауважую, що про напрям нульового вектора не говорять i абсолютна величина нульового вектора дорiвнюi нулю. Операцii над нульовими векторами вiдiграють ту саму роль, що й число нуль в операцiях числа.

РЖРЖРЖ. Тренувальнi вправи (на кодопозитивi, напiвснi ).

1. Вектори AB i DC однаково ( ) чи протилежно ( ) напрямленнi

2. Два вектори AB i DC рiвнi. Порiвняйте iхнi абсолютнi величини й напрям.

3. Вектори AB i CB рiвнi за абсолютною величиною. Чи рiвнi цi вектори?

IV. Пiдсумок уроку.

1) Пригадую з учнями як позначаiться вектор.

2) Звертаю увагу на поняття одинаковi ( ) i протилежно ( ) напрямленнi вектори i ,що такi вектори називаються колiнеарними.

3) Учнi пригадують, що вектор маi довжину, тобто нове поняття, абсолютна величина вектора.

4) Ще раз пригадую учням, про нульовий вектор i операцii над ним. На кiнець звертаю увагу, що вектор i операцii над ним використовуються у фiзицi.

IV. Домашнi завдання. Вз 10 (п. 91); №1; за. 1 тАУ 4.

B C

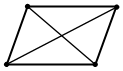
O

A D

Мал. 9

Додаткове завдання.

1) Довести, що для справедливостi рiвностi AB = CD необхiдноi i достатньо, щоб середина вiдрiзка AD збiгалася iз серединою вiдрiзка BC.

2) Позначте на мал.9 вектори AB,CB,OA, OC, BD, AD, DC, OB . Записати спiвнапрямленi i протилежно напрямленi вектори.

УРОК тАУ 2. Тема уроку. РРЖВНРЖСТЬ ВЕКТОРРЖВ. РОЗВтАЩЯЗУВАННЯ ВПРАВ

Мета уроку. Ознайомлення учнiв iз поняттям рiвнi вектори i закрiпити на прикладах.

Тип уроку. Урок засвоiння нових знань; застосування знань i формування вмiнь.

Знання, вмiння, навички. Знати формулювання рiвностi векторiв, умiти вiдкладати вiд довiльноi точки вектор, який дорiвнюi даному.

Наочнi посiбники i ТЗН. 1) Кодоскоп; 2) кодопозитиви iз зразками алгоритму розвтАЩязку вправ.

ХРЖД УРОКУ

РЖ. Фронтальне опитування.

В тАУ 1 [ В тАУ 2]

1) Вектором називаiться .. 1) Абсолютною величиною вектора називаiться

а) напрямлений вiдрiзок; а) довжина вiдрiзка;

б) вiдрiзок певноi довжини; б) довжина вектора;

в) стрiлка з напрямом; в) довжина променя;

г) промiнь. г) довжина вiдрiзка, що зображаi вектор. (1 бал)

2) Якi вектори спiв напрямленi: 2) Якi вектори протилежно напрямленi:

M A N

K B L

Мал. 10

а)BK i BL; б) NA i AN; а) LB i BK; б) NA NM. в) MN i AN; г) KM i NL; в) MK i LN; г) NM i LK. (2бали)

3) Вектор AB=3. Яка довжина вектора 3) Вектор NK=5. Яка довжина

MN, коли вектор AB= MN? вектора DC, коли NK= DC?

а) MN=6; б) MN=3; в) MN=0;г) MN=5. а) AB=5;б)AB=3;в)AB=10; г)AB=0. (3 бали)

4) Нехай ABCDтАУ квадрат OтАУточка перетину дiагоналей, |AC|= 6см. нього Δ ABC iз стороною 8 см

4) DEтАУсередня лiнiя

Чому дорiвнюi |OA|?

B C

ВаO

A D

а) |OA|= 6см ; редина BC). Знайти |AD|.

B

ВаD E

AC

б) |OA|=3см; а)|AD|=3см;

в) |OA|=6см; б)|AD|=6см;

г) |OA|=3см. в)|AD|=4см;

г)|AD|=8см. (3бали)

5) Паралельне перенесення задаiться формулами x'=x+2[x'=x+3], y'=yтАУ1

[y'=yтАУ2]. У якi точки при цьому паралельному перенесеннi переходить

початок i кiнець вектора AB [MN], що мають вiдповiднi координати (1;2) i (2;3) [ (2;4) i (1;3) ].

а) (2;3) i (4;2); б) (1;3) i (2;4); а) (5;1) i (4;0); б) (5;2) i (4;1);

в) (-3;1) i (4;-2); г) (2;1) i (-4;2). в) (-5;-2) i (-4;-1); г) (4;1) i (2;5). (3 бали)

Пiсля цього демонструю на екран правильнi вiдповiдi. Учнi виставляють оцiнки за бальною системою, яка демонструiться на екран (або таблицю). Звертаiться увага на 4-те завдання, до якого ми ще повернемося в наступних уроках.

РЖРЖ. Вивчення нового матерiалу.

Пропоную учням порiвняти вектори (4-те завдання iз тестiв фронтального опитування) BC i AD, AO i OC. Назвати пару векторiв, якi однаково напрямленi i рiвнi за абсолютною величиною. Учнi знаходять правильну вiдповiдь, пропонують своi версii означення рiвностi векторiв. Пiсля цього ввожу означення рiвних векторi:

Два вектори називаються рiвними, якщо вони сумiщаються паралельним перенесенням.

1

ВаD

C B

A

2

Показую на екранi мал. 213 (за пiдручником) i за допомогою двох кодоплiвок (плiвка-1, плiвка-2) демонструю динамiку паралельного перенесення. З екрана учнi бачать, що iснуi паралельне перенесення, яке переводить початок (С) i кiнець (D) одного вектора вiдповiдно у початок (А) i кiнець (В) другого вектора.

Пiдсумовую необхiдну i достатню умову рiвностi векторiв: тАЭрiвнi вектори однаково напрямленi й рiвнi мiж за абсолютною величиноютАЭ.

Повертаючись до екрану звертаю увагу учням, що вектори AB i CD тАУодинаково напрямленi i рiвнi за абсолютною величиною. Паралельне перенесення, яке переводить точку C у точку A, сумiщаi (учнi дивляться на екран) роблять висновок: AB = CD (вiдрiзки) i тому точка D збiгаiться з точкою B, тобто паралельне перенесення переводить вектор CD у вектор AB. Отже, вектори AB i CD рiвнi, що й треба було довести.

РЖРЖРЖ. Закрiплення матерiалу (демонструю на кодоскопi).

1. Вектори AB i DC однаково напрямленi й мають рiвну абсолютну величину. Чи рiвнi цi вектори?

2. Два вектори AB = BC. Порiвняйте iхнi абсолютнi величини i напрям.

3. Дано паралелограм ABCD. Якi векторнi рiвностi можна скласти, використовуючи малюнок 11?

5. OA, OB, OC тАУ радiуси одного кола. Що можна сказати про вектори OA, OB, OC?

6. Розглянути розвтАЩязок (за пiдручником мал. 214) задачi.

Пiсля ознайомлення учнiв iз розвтАЩязком задачi 2 i з можливiстю й однозначнiстю вiдкладання вiд будь-якоi точки площини вектора, що дорiвнюi даному(за пiдручником с. 142), пропоную розвтАЩязати таку задачу: Дано вектор АВ i точку D. Побудувати точку С так, щоб вектор DC= АВ

Скiльки розвтАЩязкiв маi задача?

В

Ваа

ВаА С

а΄

О

План побудови записую на кодоплiвцi. Учнi коментують i записують цей план у зошитi, а також виконують побудову:

1) будуiмо пiв пряму з початком у точцi D, паралельно пiв прямiй АВ (за допомогою косинця й лiнiйки);

2) на цiй пiв прямiй будуiмо точку С, яку одержимо сумiщенням з точкою В (iснуi паралельне перенесення, при якому початок вектора АВ переходить у точку D, а кiнець точки В точку С).

Таким чином вiд точки D площини вiдкладаiмо один i тiльки один вектор a΄, що дорiвнюi a.

IV. Пiдсумок уроку.

Звертаю увагу учнiв на необхiдну й достатню умову рiвностi векторiв, а також на те, що рiвнiсть векторiв iстотно вiдрiзняiться вiд рiвностi вiдрiзкiв (учнi самi роблять висновок).

V. Завдання додому. Вз10 (п. 92); №3; зап.5 тАУ 7.

Додаткова вправа.

1) ABCD тАУ квадрат, О тАУ точка перетину його дiагоналей. Чи рiвнi вектори?

AB i CD, AD i OC, AO i OB, BO i OD?

УРОК тАУ 3. Тема уроку. КООРДИНАТИ ВЕКТОРА

Мета уроку. Сформулювати поняття координати вектора, ознайомити iз знаходженням координати вектора через координати пари чисел (координата кiнцiв вектора).

Тип уроку. Урок засвоiння нових знань.

Наочнi посiбники i ТЗН. 1) кодоскоп; 2) кодопозитиви.

Знання, вмiння, навички. Знати, що таке координати вектора; формулювання прямоi i оберненоi теореми про рiвнiсть векторiв; вмiти знаходити координати вектора за його початку i кiнця; обчислювати абсолютну величину за його координатами; набути навичок при виконаннi вправ на обчислення рiвностi векторiв i iх, координат.

ХРЖД УРОКУ

РЖ. Повторення вивченого матерiалу.

Перевiрку домашнього завдання проводжу за допомогою кодоскопу. На екран демонструю алгоритм розвтАЩязку вправи № 3 (Вз10) i додаткову вправу (квадрат).

До даних вправ задаю запитання 5 тАУ 7 (за пiдручником). Один учень розповiдаi доведення запитання 6, а iнший за допомогою кодоскопу розповiдаi доведення запитання 7.

Пiсля цього активним учням виголошую оцiнки (бали).

РЖРЖ. Вивчення нового матерiалу.

1. Демонструю на екран мал. 12 (з коментуванням).

y

y₁ B(x₂;y₂)

y₁ A(x₁;y₁)

O x₁ x₂ x

Мал. 12

Задаю запитання:

1) Назвати координати точок А i В.

2) Показати на екранi АВ вiсi абсцис i ординат.

3) Записати довжини проекцiй на осi Ox i Oy.

Пояснюю, що числа a₁ = x₂ тАУ x₁ i a₂ = y₂ тАУ y₁ i довжини проекцiй вектора на осi координат i тим самим ми знайшли координати вектора.

Корисно сформулювати правило знаходження вектора:

тАЭ Щоб знайти координати вектора, потрiбно з координат його кiнця вiдняти вiдповiднi координати його початку тАЭ.

Пiдсумовую: координати векторiв (OA,OC) iз початком в точцi O(0;0) спiвпадають з координатами, iх кiнцiв.

Пропоную учням обчислити координати кiнця (початку) вектора за його координатами й координатами його початку (кiнця):

1) Знайти координати кiнця вектора (2;5), початок якого в точцi: а) (2;3); б) (-1;5), в) (0;0).

2) Знайти координати початку вектора (5;-3), кiнець якого в точцi:

а) (-3;1), б) (0;0), в) (5;-3).

Для усних обчислень використовую таблицю (на кодопозитивi).

2. Формулу для обчислення абсолютноi величини вектора за його координатами виводжу пiд час розвтАЩязування вправ (учнi по черзi на дошцi записують розвтАЩязок):

1) Дано точки А(3;1) i В(5;3). Знайдiть абсолютну величину вектора АВ.

2) Вектор а маi початком точку А(x₁;y₁) ,а кiнцем точку B(x₂;y₂).ЗнайдiтьВаабсолютну величину вектора а.

РозвтАЩязування.

| a | = | AB | = Ва= .

Пропоную учням обчислити модулi векторiв, заданих: а) координатами;

б) початку й кiнця (самостiйно на кодопозитивi).

3. Для доведення теореми про рiвнi вектори користуюся мал.13 i розпо вiдаю сам процес доведення.

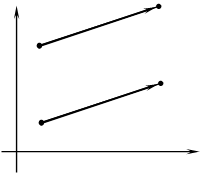y A₂(x₂; y₂)

A₁(x₁; y₂)

A₂'(x₂; y₂)

A₁'(x₁'; y₁')

O x

Мал. 13

Формулюю пряму i обернену теорему:

тАЭ Рiвнi вектори мають рiвнi вiдповiднi координати тАЭ.

РЖ навпаки:

тАЭЯкщо у векторiв вiдповiднi координати рiвнi, то вектори рiвнi тАЭ.

На кодоскопу або на таблицях демонструю доведення прямоi, i оберненоi теореми про рiвнiсть векторiв. Учнi беруть участь в обговореннi доведення.

Пряма теорема:Обернена теорема:

Дано: а = а΄. Дано: x₂ тАУx₁ = x₂΄ тАУ x₁΄_, (1)

Довести: x₂ тАУx₁ = x₂΄ тАУ x₁΄, y₂ тАУ y₁ = y₂΄ тАУ y₁΄. (2)

y₂ тАУ y₁ = y₂΄ тАУ y₁΄. Довести: а = а'.

Доведення. Нехай паралельне пере- Доведення. Знайдеться паралельне, яке перенесення водить точку А₁ в точку А₁΄. Тодi , пiдставляiмо

Ваx΄ = x + c, d = y₁΄ тАУ y₁.

Ваy΄ = y + d; РЖ

тому А΄₁ переходить в А΄₁ за допомогою паралельного перенесення:

переводить а в а΄, тобто x΄= x + x₁΄ тАУx₁, y΄= y₁΄тАУ y₁.

x΄ = x₁ + c, y₁΄ = y₁ + d, Цi рiвностi задовольняють координати точок А₂ i А₂΄ x΄₂ = x₂ + c΄, y₂΄= y₂ + d, звiдси x₂΄=x₂+x₁΄ тАУx₁ , y₂΄=y₂ + y₁΄тАУ y₁.З умови випливаi що

x₂΄ тАУ x₂΄ = x₂ тАУ x₁, iснуi паралельне перенесення: А₁ А₁΄ i А₂ А₂,΄

y₂΄ тАУ y΄₂ = y₂ тАУ y_1, що й, т. б. д. тобто вектори а й а рiвнi, що й т. б. д.

За допомогою кодоскопу (таблицi) показую скорочений запис прямоi, i оберненоi теореми: