Методика решения иррациональных уравнений и неравенств в школьном курсе математики
Вз 1. Анализ школьных учебников по алгебре и началам анализа
1.1. ВлАлгебра, 8В», авт. А. Г. Мордкович
1.2. ВлАлгебра и начала анализа, 10-11В», авт. А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницин и др.
1.3. ВлАлгебра и начала анализа, 10-11В», авт. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др.
1.4. ВлАлгебра и начала анализа, 10-11В», авт. М. И. Башмаков.
1.5. ВлАлгебра и начала анализа, 10-11В», авт. А. Г. Мордкович.
1.6. ВлСборник задач по алгебре, 8-9В», авт. М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич.
1.7. ВлАлгебра и математический анализ, 11В», авт. Н. Я. Виленкин, О.С. Ивашев-Мусатов, С. И. Шварцбурд.
Вз 2. Методика изучения иррациональных уравнений
2.1. Теоретические основы решения уравнений
2.1.1. Основные понятия, относящиеся к уравнениям
2.1.2. Наиболее важные приемы преобразования уравнений
2.2. Методы решения иррациональных уравнений
2.2.1. Метод сведения к эквивалентной системе уравнений и неравенств
2.2.2. Метод уединения радикала
2.2.3. Метод введения новой переменной.
2.2.4. Метод сведения к эквивалентным системам рациональных уравнений
2.2.5. Умножение обеих частей уравнения на функцию.
2.2.6. Решение иррациональных уравнений с использованием свойств входящих в них функций
3. Тождественные преобразования при решении иррациональных уравнений
Вз 3. Методика решения иррациональных неравенств
3.1. Теоретические основы решения иррациональных неравенств
3.2. Методы решения иррациональных неравенств
3.2.1. Метод сведения к эквивалентной системе или совокупности рациональных неравенств
3.2.2. Умножение обеих частей неравенства на функцию
3.2.3. Метод введения новой переменной
3.2.4. Решение иррациональных неравенств с использованием свойств входящих в них функций
Вз 4. Опытное преподавание
Заключение
Список библиографии
Приложение А
Приложение Б
Приложение В
Введение
Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики. Одним из сложных разделов алгебры, изучаемых в школьной программе, являются иррациональные уравнения и неравенства, так как в школе им уделяют достаточно мало внимания.
Трудности при изучении данного вида уравнений и неравенств связаны со следующими их особенностями:
В· в большинстве случаев отсутствие четкого алгоритма решения иррациональных уравнений и неравенств;
В· при решении уравнений и неравенств данного вида приходится делать преобразования, приводящие к уравнениям (и неравенствам), не равносильным данному, вследствие чего чаще всего возникают ошибки, которые обычно связаны с потерей или приобретением посторонних корней в процессе решения.
Опыт показывает, что учащиеся в недостаточной степени овладевают умением решать иррациональные уравнения и неравенства, часто допускают ошибки при их решении. Однако задачи по теме ВлИррациональные уравнения и неравенстваВ» встречаются на вступительных экзаменах, и они довольно часто становятся Влкамнем преткновенияВ».
Выше изложенное обусловило проблему исследования: обучение школьников решению иррациональных уравнений и неравенств, используя при этом основные методы решения иррациональных уравнений различных видов.
Объектом исследования является процесс обучения алгебре в 7-9 классах и алгебре и началам анализа в 10-11 классах.
Предметом исследования являются различные виды иррациональных уравнений и неравенств и методы их решения.
Целью работы является разработка методики изучения учащимися иррациональных уравнений и неравенств в школе.
Гипотеза исследования: освоение умения различать основные виды иррациональных уравнений и неравенств, умения применять необходимые приемы и методы их решения позволит учащимся решать иррациональные уравнения и неравенства на сознательной основе, выбирать наиболее рациональный способ решения, применять разные способы решения, в том числе те, которые не рассмотрены в школьных учебниках.
Для достижения поставленной цели и проверки гипотезы необходимо решить следующие задачи:
1. проанализировать действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств;
2. изучить стандарты образования по данной теме;
3. изучить статьи и учебно-методическую литературу по данной теме;
4. подобрать теоретический материал, связанный с равносильностью уравнений и неравенств, равносильностью преобразований, методами решения иррациональных уравнений и неравенств;
5. рассмотреть основные методы и приемы решения различных иррациональных уравнений и неравенств;
6. подобрать примеры решения иррациональных уравнений и неравенств для демонстрации излагаемой теории;
7. разработать
8. осуществить опытное преподавание.
Вз 1. Анализ школьных учебников по алгебре и началам анализа
При изучении любой новой темы в основном курсе школы встает проблема изложения данной темы в школьных учебниках. Пропедевтикой изучения раздела иррациональных уравнений и неравенств в школе является введение понятие арифметического корня и, соответственно, рассмотрение его свойств.
Проанализируем в каких классах вводится данное понятие разными авторами учебников. Алимов Ш. А. в учебнике ВлАлгебра. 9классВ» вводит понятие арифметического корня натуральной степени, а также свойства арифметического корня. Макарычев Н. Г. же разделяет понятия квадратного корня и корня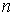 
-ой степени. В учебнике ВлАлгебра. 8 классВ» классе вводится понятие арифметического квадратного корня и, соответственно, рассматриваются его свойства. В учебнике ВлАлгебра. 9 классВ» вводятся понятия корня 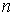-ой степени, арифметического корня 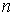-ой степени и рассматриваются свойства арифметического корня 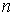-ой степени. Колмогоров А. Н. в учебнике ВлАлгебра. 10 классВ» вводит понятия корня 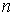-ой степени, арифметического корня 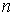-ой степени и рассматривает свойства арифметического корня 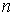-ой степени перед изучением иррациональных уравнений. Мордкович А. Г. в учебнике ВлАлгебра. 8 классВ» вводит понятие квадратного корня и его свойства. Кроме того, в этом же учебнике есть отдельный параграф, посвященный иррациональным уравнениям.
1.1. ВлАлгебра, 8В», авт. А. Г. Мордкович [27], [28]
Данное учебное пособие состоит из двух частей: учебника и задачника.
В I части данного учебного пособия материал, посвященный иррациональным уравнениям, изложен в главе ВлКвадратные уравненияВ» в параграфе ВлИррациональные уравненияВ». Параграф начинается с определения иррационального уравнения. Далее рассматривается решение иррационального уравнения 
Вапо определению квадратного корня из чего выводится метод решения иррациональных уравнений тАУ метод возведения в квадрат обеих частей уравнения. Затем данный метод демонстрируется на примерах решения иррациональных уравнений вида 
, 
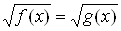. Найденные корни проверяются подстановкой в исходное уравнение, при этом обращено внимание на те случаи, когда могут появиться посторонние корни. Автор подчеркивает, что проверка тАУ обязательный этап решения иррационального уравнения. Далее приводится решение уравнения вида 
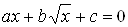Ваметодом введения новой переменной 
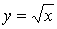. Параграф завершается беседой о равносильных и неравносильных преобразованиях: дается определение равносильных уравнений, перечисляются и демонстрируются на примерах равносильные и неравносильные преобразования.
Система задач во II части данного учебного пособия достаточно разнообразна. В №№ 1011-1014 необходимо решить иррациональные уравнения вида , где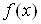 
ВатАУ линейное, квадратное или дробно-рациональное выражение. В № 1015 чтобы решить уравнение необходимо сначала уединить радикал. В № 1016 для решения предложены уравнения вида 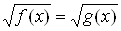. №№ 10017-1020 тАУупражнения для решения методом замены иррациональных уравнений вида , 
, 
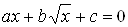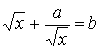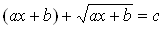. В №№ 1023, 1024 необходимо выяснить, равносильны ли уравнения. В №№ 1021, 1022, 1025-1027 нужно решить уравнения вида 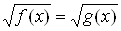, , где выражения , 
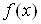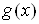могут быть как линейными так и квадратными, а в №№ 1028-1031 тАУ уравнения вида 
.
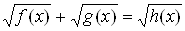№№ 1032, 1033 тАУ упражнения повышенной трудности для решения иррациональных уравнений методом замены.
Теперь проанализируем действующие учебники по алгебре и началам математического анализа для 10-11 классов, чтобы выяснить, как в них представлены методы решения иррациональных уравнений и неравенств.
1.2. ВлАлгебра и начала анализа, 10-11В», авт. А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницин и др. [13].
Материал по данной теме изложен в IV главе ВлПоказательная и логарифмическая функцииВ», как пункт ВлИррациональные уравненияВ» параграфа ВлОбобщение понятия степениВ». Автор рекомендует рассматривать решение иррациональных уравнений в теме ВлУравнения, неравенства, системыВ», где систематизируются сведения об уравнениях.
В пункте ВлИррациональные уравненияВ» дается понятие иррационального уравнения, приводится несколько примеров простейших иррациональных уравнений вида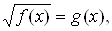 
, которые решаются с помощью возведения обеих частей уравнения в квадрат. Найденные корни проверяются подстановкой в исходное уравнение, при этом обращено внимание на те случаи, когда могут появиться посторонние корни. Показано, что кроме возведения в квадрат иррациональные уравнения удобно решать, используя равносильный переход от уравнения к системе, состоящей из уравнения и неравенства. Рассмотрен пример иррационального уравнения, содержащего корень третьей степени. Для того чтобы Влизбавиться от радикалаВ», обе части такого уравнения возводятся в куб.
После пункта приведены упражнения для закрепления умений решать иррациональные уравнения. В №№417-420 предложены простейшие уравнения вида 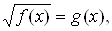, решить которые можно с помощью возведения обеих частей уравнения либо в квадрат, либо в куб, а также используя равносильные переходы. Такие задачи, по мнению авторов учебника необходимо уметь решать для получения удовлетворительной оценки. Задачи же в №№422-425 чуть сложнее. Здесь уравнения содержат корни выше третьей степени.
Иррациональным неравенствам в данном пункте внимания не уделено.
В заключительной главе учебника ВлЗадачи на повторениеВ» помещены практические упражнения для повторения курса. Здесь в параграфе ВлУравнения, неравенства, системы уравнений и неравенствВ» иррациональным уравнениям и неравенствам посвящен пункт ВлИррациональные уравнения и неравенстваВ». То есть, не смотря на то, что в основной части учебника иррациональным неравенствам внимания не уделено, автор включает в задания для повторения такие неравенства.
1.3. ВлАлгебра и начала анализа, 10-11В», авт. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. [1].
В данном учебнике нет материала, посвященного иррациональным уравнениям и неравенствам. Лишь в конце ученика помещены упражнения для итогового повторения курса алгебры. Здесь есть только один номер для решения простейших иррациональных уравнений (№801). Упражнений для решения иррациональных неравенств нет.
Это можно объяснить тем, что, по мнению автора, умение решать иррациональные неравенства не является обязательным для учащихся и соответствующая тема может быть предложена для изучения самостоятельно или на факультативных занятиях. [14] Поэтому в учебнике предложены задачи для внеклассной работы, где встречаются иррациональные уравнения (№№934, 947) и неравенства (№942).
1.4. ВлАлгебра и начала анализа, 10-11В», авт. М. И. Башмаков [2].
В данном учебном пособии иррациональные уравнения и неравенства рассматриваются в заключительной VI главе ВлУравнения и неравенстваВ». Глава предназначена для систематизации и обобщения сведений об уравнениях, неравенствах и системах уравнений. В начале главы помещена вводная беседа, которая состоит из трех пунктов.
В пункте ВлУравнениеВ» вводятся такие понятия как уравнение, неизвестные, корень уравнения, подробно рассказывается, что значит решить уравнение с одним или двумя неизвестными, что означает найти корни уравнения, приведены некоторые рекомендации о форме записи ответа при решении уравнений с одним или двумя неизвестными.
В пункте ВлРавносильностьВ» выясняется, когда одно уравнение является следствием другого, вводится понятие равносильных уравнений. Автор подробно останавливается на некоторых полезных преобразованиях уравнений:
1) Перенос членов из одной части уравнения в другую с противоположным знаком.
2) Переход к совокупности уравнений.
3) Переход к системе уравнений.
Все равносильные переходы представлены в виде схем и рассмотрены на примерах.
В следующем пункте ВлНеравенствоВ» приведены примеры верных и неверных числовых неравенств, основные правила преобразования неравенств, при этом используются знаки следствия и равносильности. Вводятся такие понятия как ОДЗ неравенства, решение неравенства, равносильные неравенства, выясняется, когда одно неравенство является следствием другого.
Вз1 ВлУравнения с одним неизвестнымВ» состоит из трех пунктов: ВлОбщие приемыВ», ВлПримеры решения уравненийВ» и ВлПриближенные методы вычисления корнейВ». В первом пункте перечислены стандартные уравнения, которые были изучены ранее. Основным шагом в решении уравнения является преобразование уравнения к одному из стандартных. Приведены некоторые наиболее употребительные приемы, общие для всех типов уравнений:
1) Разложение на множители.
2) Введение нового неизвестного.
3) Графический метод.
Отметим, что во втором пункте на ряду со стандартными уравнениями рассматривается решения только одного простейшего иррационального уравнения с помощью равносильного перехода к системе.
В третьем пункте кратко рассказывается о таких методах приближенного вычисления корней как метод половинного деления, метод хорд и касательных.
Вз 2 ВлНеравенства с одним неизвестнымВ» состоит из двух пунктов: ВлОбщие приемыВ» и ВлПримеры решения неравенствВ». В первом пункте демонстрируется два приема решения неравенств: разложение на множители и метод замены неизвестного.
Во втором пункте на примерах показана техника решения неравенств с помощью переходов, сохраняющих равносильность. Отметим, что на ряду со стандартными неравенствами рассматривается решение только одного простейшего иррационального неравенства.
В конце главы помещены задания для решения иррациональных уравнений №17, для решения иррациональных неравенств тАУ №21, в котором есть задание со звездочкой, то есть относящееся к разделу Влтрудные задачиВ».
Иррациональным уравнениям и неравенствам в главе уделено недостаточно внимания: приведены решения с помощью переходов, сохраняющих равносильность одного простейшего иррационального уравнения и одного неравенства.
Цель данной главы тАУ обобщить имеющиеся у учащихся знаний об уравнениях, неравенствах и системах уравнений, поэтому здесь подробно не рассматриваются конкретные виды уравнений, а лишь повторяются сведения об изученных видах уравнений и методах их решения. [14]
1.5. ВлАлгебра и начала анализа, 10-11В», авт. А. Г. Мордкович
[10], [11].
Данное учебное пособие состоит из двух частей: учебника и задачника.
В I части данного учебного пособия материал, касающийся иррациональных уравнений и неравенств, изучается в последней VIII главе ВлУравнения и неравенства. Системы уравнений и неравенствВ», завершающей изучение школьного курса алгебры и начал математического анализа. Здесь уравнения и неравенства рассматриваются с самых общих позиций. Это, с одной стороны, своеобразное подведение итогов и, с другой стороны, некоторое расширение и углубление знаний.
В первых трех параграфах этой главы подведены итоги изучения в школе уравнений, неравенств. Использованы следующие термины:
¨ равносильность уравнений, равносильность неравенств;
¨ следствие уравнения, следствие неравенства;
¨ равносильное преобразование уравнения, неравенства;
¨ посторонние корни (для уравнений);
¨ проверка корней (для уравнений).
Сформулированы теоремы:
¨ о равносильности уравнений;
¨ о равносильности неравенств.
Даны ответы на четыре главных вопроса, связанных с решением уравнений:
1) как узнать, является ли переход от одного уравнения к другому равносильным преобразованием;
2) какие преобразования переводят данное уравнение в уравнение-следствие;
3) как сделать проверку, если она сопряжена со значительными трудностями в вычислениях;
4) в каких случаях при переходе от одного уравнения к другому может произойти потеря корней и как этого не допустить?
Перечислены возможные причины расширения области определенияуравнения, одна из которых тАУ освобождение в процессе решения уравнения от знаков корней четной степени; указаны причины, по которым может произойти потеря корней при решении уравнений.
Выделены четыре общих метода решения уравнений:
1) замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x);
2) метод разложения на множители;
3) метод введения новых переменных;
4) функционально-графический метод.
Что касается иррациональных уравнений, то им в данном учебном пособии уделено достаточно большое внимание.
На примере иррационального уравнения показано как решение любого уравнения осуществляется в три этапа: технический, анализ решения, проверка.
Также на примере иррационального уравнения показано, как сделать проверку, если проверка корней с помощью их подстановки в исходное уравнение сопряжена со значительными вычислительными трудностями.
Метод замены уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x) применятся при решении иррациональных уравнений для перехода от уравнения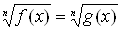 
Вак уравнению 
.
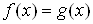Метод введения новой переменной также разобран и на примере решения иррационального уравнения.
Отдельный пункт посвящен иррациональным неравенствам. Здесь с теоретическим обоснованием рассматривается решение неравенств вида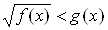 
, 
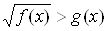. В первом случае иррациональное неравенство заменяется равносильной системой неравенств 
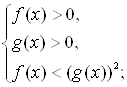Ваво втором тАУ равносильной совокупностью систем неравенств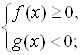 
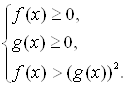
Система задач во II части данного учебного пособия изложена в той же последовательности, что и соответствующий материал в I части. В Вз 55 ВлРавносильность уравненийВ» изложены различные типы заданий на равносильность и следствие уравнений, в том числе и иррациональных. В Вз 56 ВлОбщие методы решения уравненийВ» помещены задания для использования четырех методов, изложенных в I части данного учебного пособия, для решения уравнений. Все задачи в соответствии с ними разбиты на четыре блока, в каждом из которых встречаются иррациональные уравнения. В Вз 57 ВлРешение неравенств с одной переменнойВ» изложены различные типы заданий на равносильность и следствие неравенств, в том числе и иррациональных.
В № 1673 нужно решить простейшие иррациональные уравнения. №№1674, 1675, 1712-1719 тАУ упражнения выше среднего уровня для решения иррациональных уравнений, №№1790, 1791 тАУ неравенств. № 1792 тАУ упражнение повышенной трудности для решения иррациональных неравенств.
Много заданий, в которых требуется решить ВлсмешанноеВ» уравнение или неравенство, то есть логарифмическое, показательное или тригонометрическое уравнение или неравенство, в которое входят и иррациональные выражения. Среди этих заданий есть задания как базового, так и повышенного уровня.
В I части учебника много внимание уделено равносильности уравнений и неравенств, достаточно строго рассмотрены общие методы решения уравнений, с оговоркой о потере корней и приобретении посторонних. II часть учебника отличается обилием и разнообразием задач. Достаточно много задач на равносильность и следствие уравнений и неравенств.
1.6. ВлСборник задач по алгебре, 8-9В», авт. М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич [5].
Данная книга представляет собой сборник задач по курсу алгебры, предназначенный для учащихся 8-9 классов с углубленным изучением математики.
В начале параграфа ВлСтепень с рациональным показателемВ» помещен справочный материал теоретического характера, посвященный иррациональным уравнениям и неравенствам. Описаны такие пути решения иррациональных уравнений, как:
В· возведение обеих частей уравнения в натуральную степень с последующей проверкой найденных корней;
В· переход к равносильным системам, в которых учитывается область определения уравнения и требование того, что бы были неотрицательными обе части уравнения, возводимые в четную степень.
При решении иррациональных неравенств либо используется метод интервалов, либо с помощью равносильных преобразований заменяется данное иррациональное неравенство системой (или совокупностью систем) рациональных неравенств.
В параграфе рассмотрено три способа решения иррационального уравнения вида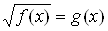 
:
1) переход к равносильной системе;
2) введение новой переменной;
3) использование свойства монотонности функций.
Среди упражнений, помещенных в данном параграфе, есть упражнения для закрепления умений и навыков решать иррациональные уравнения и неравенства. В №№115-117 необходимо доказать, что уравнение не имеет решения, в №№118-119 тАУ ответить на вопрос: равносильны ли уравнения. №№120-144 предлагаются для решения иррациональных уравнений, №№145-155 тАУ для решения неравенств описанными выше способами.
1.7. ВлАлгебра и математический анализ, 11В», авт. Н. Я. Виленкин, О.С. Ивашев-Мусатов, С. И. Шварцбурд [4].
Данное учебное пособие представляет собой продолжение книги ВлАлгебра и начала анализаВ» для 10 класса и предназначено как для общеобразовательной школы, так и классов и школ с углубленным изучением курса математики.
Иррациональные уравнения и неравенства изучаются в параграфе ВлСтепенная функция. Иррациональные выражения, уравнения и неравенстваВ» VIII главы ВлПоказательная, логарифмическая и степенные функцииВ».
Пункт ВлИррациональные уравненияВ» начинается с определения иррационального уравнения и примеров таких уравнений. Далее сформулирована и доказана теорема о равносильных уравнениях, на которой основано решение иррациональных уравнений. Из теоремы следует, что если в ходе решения иррационального уравнения приходилось возводить обе его части в степень с четным показателем, то могут появиться посторонние корни. Поэтому, чтобы не было необходимости подставлять найденные корни в данное уравнение, сформулировано еще два утверждения о равносильном переходе от уравнений вида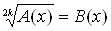 
Ваи 
Вак системам, состоящим из уравнения и неравенства. Далее на примерах решения иррациональных уравнений демонстрируются данные равносильные переходы. Также автор рекомендует перед возведением обеих частей уравнения в некоторую степень Влуединить радикалВ», то есть представить уравнение в виде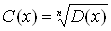 
. Далее данный метод применяется для решения иррациональных уравнений
После данного пункта помещены упражнения для закрепления умений решать иррациональные уравнения описанными выше методами тАУ №216. В №215 необходимо доказать, что данные иррациональные уравнения не имеют решений.
В следующем пункте ВлИррациональные неравенстваВ» сформулированы приемы решения иррациональных неравенств вида 
Ваи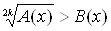 
Вас помощью равносильного перехода к системе неравенств в первом случае и совокупности систем неравенств тАУ во втором. Рассматривается решение иррационального неравенства вида 
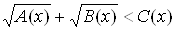Вас помощью равносильного перехода к неравенству 
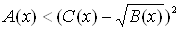. Решение каждого из видов неравенств демонстрируется на примерах.
После данного пункта помещены упражнения (№217) для закрепления умения решать иррациональные неравенства с помощью равносильных переходов, описанных выше.
Все утверждения, сформулированные в данном учебном пособии, изложены со строгим обоснованием. Описан полезный метод при решении иррациональных уравнений тАУ метод Влуединения радикалаВ». Не смотря на то, что учебник не отличается обилием упражнений, предлагаемые задания разнообразны, различной степени сложности
Проведенный анализ позволяет сделать следующие выводы:
1) В учебнике [1] материала по методам решения иррациональных уравнений нет. В учебниках [13] и [4] материала по теории способов решения иррациональных уравнений достаточно. В большом объеме теория по общим методам решения рассмотрена учебнике [2] и [10].
2) В каждом учебнике рассмотрены два основных способа решения: возведение обеих частей уравнения в степень, с последующей подстановкой полученных корней в исходное уравнение, а также решение уравнений с помощью равносильных переходов к системе, состоящей из уравнения и неравенства. В учебниках [2] и [10] рассмотрены такие общие методы решения уравнений как метод разложения на множители, метод введения новых переменных, функционально-графический метод; некоторые из них продемонстрированы на примерах решения иррационального уравнения.
3) В учебниках [1] и [13] не рассмотрено решение иррациональных неравенств. В учебнике [2] материала по решению иррациональных неравенств не достаточно. В учебниках [4] и [10] подробно и с теоретическим обоснованием рассмотрено решение иррациональных неравенств вида 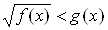, 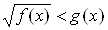Вас помощью равносильного перехода к системе (или совокупности систем). Только в учебнике [4] рассматривается решение иррационального неравенства вида .
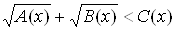4) Наиболее большой объем упражнений для решения иррациональных уравнений и неравенств представлен в учебниках [11] и [5]. В учебнике [4] упражнений немного, но они разнообразны.
Вз 2. Методика изучения иррациональных уравнений
2.1. Теоретические основы решения уравнений
2.1.1. Основные понятия, относящиеся к уравнениям
Равенство вида
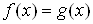,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(1)
где 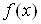Ваи 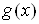ВатАУ некоторые функции, называют уравнением с одним неизвестным x (с одной переменной x). Это равенство может оказаться верным при одних значениях x и неверным при других значениях x.
Число a называется корнем (или решением) уравнения (1), если обе части уравнения (1) определены при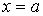 
Ваи равенство 
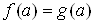Ваявляется верным. Следовательно, каждый корень уравнения (1) принадлежит множеству, которое является пересечением (общей частью) областей определения функци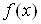й Ваи 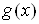Ваи называется областью допустимых значений (ОДЗ) уравнения (1).
Решить уравнение тАУ значит найти все его корни или доказать, что корней нет.
Если в условиях задачи не указано, на каком множестве нужно решить уравнение, то решение следует искать в ОДЗ этого уравнения.
В процессе решения часто приходится преобразовывать уравнение, заменяя его более простым (с точки зрения нахождения корней). Есть одно правило, которое не следует забывать при преобразовании уравнений: нельзя выполнять преобразования, которые могут привести к потере корней.
Назовем преобразование уравнения (1) допустимым, если при этом преобразовании не происходит потери корней, то есть получается уравнение
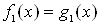,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)
которое либо имеет те же корни, что и уравнение (1), либо, кроме всех корней уравнения (1), имеет хотя бы один корень, не являющийся корнем уравнения (1), посторонний для уравнения (1) корень. В связи с этим используют следующие понятия.
Уравнение (2) называется следствием уравнения (1), если каждый корень уравнения (1) является корнем уравнения (2).
Уравнения (1) и (2) называются равносильными (эквивалентными), если каждое из этих уравнений является следствием другого. Иными словами, уравнения (1) и (2) равносильны, если каждый корень уравнения (1) является корнем уравнения (2) и наоборот, каждый корень уравнения (2) является корнем уравнения (1). Уравнения, не имеющие корней, считаются равносильными.
Если уравнения (1) и (2) равносильны, то пишут
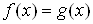
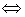
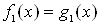Ваили (1)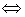(2),
а если уравнение (2) является следствием уравнения (1), то пишут
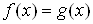
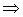
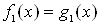Ваили (1)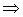(2).
Отметим, что если исходное уравнение с помощью допустимых преобразований заменено другим, причем в процессе преобразования хотя бы один раз уравнение заменялось неравносильным ему следствием, то проверка найденных корней путем подстановки в исходное уравнение является обязательной.
Если же при каждом преобразовании уравнение заменялось равносильным, то проверка не нужна (не следует путать проверку с контролем вычислений).
Рассмотрим еще одно понятие, связанное с решением уравнений. Будем говорить, что уравнение (1) равносильно совокупности уравнений
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВа(3)
если выполнены следующие условия:
1) каждый корень уравнения (1) является корнем, по крайней мере, одного из уравнений (3);
2) любой корень каждого из уравнений (3) является корнем уравнения (1).
Если указанные условия выполнены, то множество корней уравнения (1) является объединением множеств корней уравнений (3).
Если уравнение записано в виде
,ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
то каждое решение этого уравнения является решением, по крайней мере, одного из уравнений
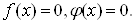ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)
Однако нельзя утверждать, что любой корень каждого из уравнений (5) есть корень уравнения (4).
Например, если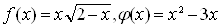 
, то 
ВатАУ корень уравнения 
, но число 3 не является корнем уравнения (4), так как функция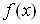 
Ване определена при .
Таким образом, в общем случае нельзя утверждать, что уравнение (4) равносильно совокупности уравнений (5). Чтобы решить уравнение (4), достаточно найти корни уравнений 
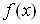Ваи , а затем отбросить те, которые не входят в ОДЗ уравнения (4), то есть не принадлежат множеству, на котором определены функции Ваи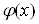 
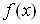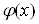. В ОДЗ уравнения (4) это уравнение равносильно совокупности уравнений (5). Справедливо более общее утверждение: если функция Ваопределена при всех xтаких, что , а функция Ваопределена при всех xтаких, что , то уравнение (4) равносильно совокупности уравнений (5). [18]
2.1.2. Наиболее важные приемы преобразования уравнений
Все преобразования уравнений можно разделить на два типа: [15]
1) Равносильные, то есть преобразования, после применения любых из которых получится уравнение, равносильное исходному.
2) Неравносильные, то есть преобразования, после применения которых может произойти потеря или приобретение посторонних корней.
Рассмотрим некоторые виды преобразований уравнений и проанализируем, к каким типам они относятся.
1. Перенос членов уравнения из одной части в другую, то есть переход от уравнения
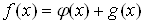ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)
к уравнению
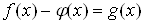.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(2)
Указанное преобразование приводит к равносильному уравнению, то есть (1)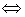(2).
В частности, 
. Заметим, что здесь речь идет только о переносе членов уравнения из одной его части в другую без последующего приведения подобных членов (если таковые имеются). [18]
2. Приведение подобных членов, то есть переход от уравнения
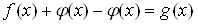ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)
к уравнению
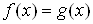.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)
Справедливо следующее утверждение: для любых функций ,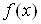
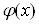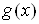, Вауравнение (4) является следствием уравнения (3), то есть (3)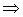(4).
Переход от уравнения (3) к уравнению (4) является допустимым преобразованием, при котором потеря корней невозможна, но могут появиться посторонние корни.
Таким образом, при приведении подобных членов, а также при отбрасывании одинаковых слагаемых в левой и правой частях уравнения получается уравнение, являющееся следствием исходного уравнения. [18]
Например, если в уравнении
вычеркнуть в левой и правой его частях слагаемое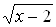 
, то получится уравнение
,
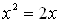являющееся следствием исходного: второе уравнение имеет корни 
, 
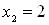, а первое тАУ единственный корень 
.
Отметим еще, что если ОДЗ уравнения (4) содержится в области определения функции 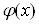, то уравнения (3) и (4) равносильны.
3. Умножение обеих частей уравнения на одну и ту же функцию, то есть переход от уравнения (4) к уравнению
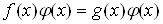.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (5)
Справедливы следующие утверждения:
1) если ОДЗ уравнения (4), то есть пересечение областей определения функци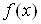й Ваи 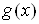, содержится в области определения функции 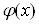, то уравнение (5) является следствием уравнения (4);
2) если функция 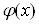Ваопределена и отлична от нуля в ОДЗ уравнения (4), то уравнения (4) и (5) равносильны. [18]
Заметим, что в общем случае переход от уравнения (5) к уравнению (4) недопустим, так как это может привест
Вместе с этим смотрят:
WEB-дизайн: Flash технологии
РЖiрархiчна структура управлiння фiзичною культурою i спортом в Хмельницькiй областi у м. КамтАЩянець-Подiльському
РЖгрова дiяльнiсть в групi продовженого дня
РЖнновацiйнi методи навчання на уроках зарубiжноi лiтератури
РЖнтенсифiкацiя навчального процесу у вищiй школi