Проблема Ферма для простых показателей больше 3

Утверждение великого французского математика Пьера Ферма (1601 тАУ 1665) о том, что неопределенное уравнение Xn + Yn = Zn не имеет решений в целых (не равных нулю) рациональных числах для n > 2 признано мировым математическим сообществом верным, после представления в 1995 г. его доказательства группой математиков Оксфордовского университета во главе с английским математиком Эндрю Уайльсом.

Это утверждение великого француза, получившее название Проблема Ферма или Великая теорема Ферма (она же ВлБольшаяВ» или ВлПоследняяВ»), более чем 300 лет оставалось проблемной задачей теории чисел. Свое УтверждениеПьер Ферма написал на полях книги Диофанта ВлАрифметикаВ» и сопроводил его следующим известным комментарием: тАЬЯ открыл этому поистине чудесное доказательство, которое из-за недостатка места не может разместиться на этих поляхтАЭ.[3]

Этот комментарий Пьера Ферма (учитывая его авторитет) указывал на возможность решения Проблемы в рамках математических знаний XVII века, это обстоятельство и другие, социально тАУ психологические причины, толкали сотни любителей математики на поиск элементарного решения Великой теоремы.

Проблема Ферма вышла за пределы математического сообщества, стала популярной, привлекая к себе не только сотни любителей математики, но и представителей культуры, которые сделали ее неким украшением художественных героев.

Показанный С.П. Капица фильм ВлЧерт и математикВ» в одной из передач ВлОчевидное тАУ НевероятноеВ» в начале 70-х годов прошлого столетия и его комментарий послужили толчком моего увлечения этой Проблемой.

В основе настоящей работы лежит моя книжка тАЬПроблема Ферма и другоетАЭ2008 г. выпуска, в которой отсутствовало доказательство ПФ 2-го случая для простых показателей вида 6n + 5.

Известно, что для показателя n = 4 Проблема решена Пьером Ферма, а для показателя n = 3 доказана гениальным Леонардом Эйлером, а потому я стал искать решение приведенного уравнения для простых показателей P> 3 т.е. для простых показателей вида 6n + 5 и вида 6n = 1.

Элементарные алгебраические преобразования многочленов, вспомогательные числа, и вспомогательные сравнения позволили найти элементарное доказательство Проблемы, если не считать примененный в работе метод сравнения чисел по модулю, введенный в математику К.Ф.Гауссом (1777 тАУ 1855).

1.Проблемы ФермаВа для простых показателей > 3

Доказательство Великой теоремыВа для простых показателей вида 6n + 1Ва иВа для простых показателей вида 6n + 5

Множество простых чисел > 3 разбиваем на два класса: на класс простых чисел вида 6n + 1 и на класс простых чисел вида 6n + 5.

Докажем сначала вспомогательные утверждения.

1.1 Вспомогательные утверждения

Теорема 1.1. Для любого простого числа P > 2 существуют целые числа, которые обозначим через А1, А2, А3, тАж, Ar, тАж, АPтАУ1/2, такие, что для любых чисел Z и X выполняется:

ZP тАУ XP = (Z тАУ X)P + A1ZX(Z тАУ X)PтАУ2 + A2Z 2X 2(Z тАУ X)PтАУ4 +

+ A3Z 3X 3(Z тАУ X)PтАУ6 + А4Z 4X 4(Z тАУ X)РтАУ8+ тАж +AРтАУ3/2 ´

´ ZPтАУ3/2XPтАУ3/2(Z тАУ X)3 + APтАУ1/2 ZРтАУ1/2 XРтАУ1/2 (Z тАУ X), ВаВаВаВаВаВаВаВаВа (1.1)

при этом числа A1 = AРтАУ1/2 = P, а числа А2, А3,тАж, Ar, тАж, АРтАУ3/2 тАУ целые и кратные Р. Доказательство. Пусть имеем многочлен вида

(Z тАУ X)PтАУ1 + A1ZX (Z тАУ X)PтАУ3 + A2Z 2 X 2 (Z тАУ X)PтАУ5 +

+ А3Z 3 X 3 (Z тАУ X)P-7+ A4Z 4 X 4 (Z тАУ X)РтАУ9+тАжВаВаВа .. + AРтАУ3/2 Z PтАУ3/2 X РтАУ3/2 (Z тАУ X)2 + AРтАУ1/2Z РтАУ1/2 X PтАУ1/2 . ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа Ва(1.2)

Покажем, что существуют такие целые числа (кратные Р) A1, A2, тАж, AРтАУ1/2, что многочлен (1.2) тождественно равен многочлену вида:

Z PтАУ1 + Z PтАУ2X + Z PтАУ3X 2 + тАж+ Z 2X PтАУ3 + ZX PтАУ2 + X PтАУ1. Ва (1.3)

Пусть многочлены (1.2) и (1.3) тождественно равны, тогда их коэффициенты при подобных членах будут равны.

Чтобы сравнить коэффициенты при подобных членах многочленов (1.2) и (1.3) воспользуемся табл. 1. Благодаря равенству биноминальных коэффициентов от начала и конца разложения бинома Ньютона в табл. 1 внесены коэффициенты от начала разложения соответствующих биномов многочлена (1.2) до серединного их члена (включительно) (строки 1, .., Р + 1/2).

В строке 1 записаны биноминальные коэффициенты разложения бинома (Z тАУ X)PтАУ1.

В строке 2 (начиная со столбца 2) записаны биноминальные коэффициенты разложения бинома (Z тАУ X)PтАУ3, умноженные на число А1.

В строке 3 (начиная со столбца 3) записаны биноминальные коэффициенты разложения бинома (Z тАУ X)PтАУ5, умноженные на число А2 и т. д.

B строке (РтАУ1)/2 записаны (начиная со столбца (РтАУ1)/2)биноминальные коэффициенты разложения бинома (ZтАУX)2, умноженные на число АРтАУ3/2.

В строке (Р+1)/2 записан коэффициент последнего члена многочлена (1.2) тАУ число АРтАУ1/2.

В последней строке табл. 1 записаны коэффициенты многочлена (1.3), которые равны +1.

Обратим внимание на то, что в каждом столбце табл. 1 (до строки Р + 1/2 включительно) записаны все коэффициенты подобных членов многочлена (1.2), а в строке без номера записаны коэффициенты членов многочлена (1.3).

Это обстоятельство позволяет вычислять числа А1, А2, тАж

Суммируя последовательно коэффициенты столбцов табл. 1 от столбца 2 до столбца (Р + 1)/2 и приравнивая полученные суммы (в силу тождества (1.2) и (1.3)) к (+1), получим значения чисел А1, А2,

Из столбца 2 получим 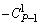Ва+ А1 = 1, тогда А1 = 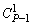+ 1, отсюда

А1 = Р. ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1.4)

Таблица 1.Таблица коэффициентов

	1	2	3	4	5	.	.	тАж	тАж	p тАУ 1/2	P + 1/2
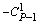
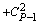
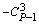
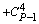
1	+1					.	.	.	.	тАж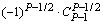
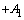
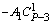
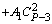
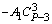
2						.	.	.	.	тАж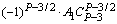
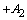
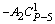
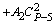
3						.	.	.	.	тАж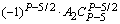
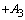
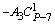
4						.	.	.	.	тАж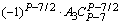
5						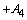.	.	.	.	тАж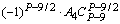
.						.	.	.	.	тАж
.							.	.	.	тАж
.								.	.	тАж
.									.	тАж
PтАУ1/2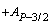
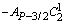
P+1/2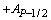
	+ 1	+ 1	+ 1	+ 1	+ 1	.	.	.	.	+ 1	+ 1