Використання можливостей системи Wolfram Mathematica при вивченi математичного аналiзу
ВступНа сьогоднiшнiй день в широких колах користувачiв обчислювальних машин став досить Вапопулярним i широко використовуваним термiн Влкомп'ютерна математикаВ». Дане поняття включаi сукупнiсть як теоретичних i методичних засобiв, так i сучасних програмних i апаратних засобiв [10].
Попит на унiверсальнi i спецiалiзованi програмнi пакети для вирiшення рiзних прикладних завдань викликав появу на ринку програмних продуктiв систем комп'ютерноi математики (СКМ), якi швидко стали популярними.
В останнi роки в процес математичноi освiти дедалi наполегливiше i успiшнiше впроваджуються такi системи, як DERIVE, MatLab, Maple, MuPAD, Mathematica та iн. Вони звiльняють користувача вiд проведення громiздких, рутинних викладок, однотипних обчислень i дозволяi зосередитися безпосередньо на аналiзi модельованого явища. Дiалог з пакетом СКМ вiдбуваiться на досить природнiй мовi, використовуються традицiйнi позначення i способи написання формул. Безсумнiвним достоiнством сучасних СКМ i прекраснi графiчнi можливостi, що дозволяi зробити наочними багато математичних понять i методiв.
У викладацькому середовищi математикiв iснуi обТСрунтоване побоювання, що використання систем комп'ютерноi математики "зiпсуi" математичну пiдготовку студентiв, подiбно до того, як "калькулятор розучив iх рахувати". Вихiд бачиться у роз'ясненнi призначення та використання СКМ. Очевидно, що успiшне використання СКМ можливо лише за умови знання основ математики. Бiльше того, щоб використати всi можливостi таких пакетiв як MatLab, Maple, Mathematica потрiбна дужа висока математична культура [7, c. 3].
А також, при залученнi СКМ для обчислень потрiбно пам'ятати, що використовувати обчислювальну систему не завжди просто. Для одних i тих же завдань система може пропонувати кiлька варiантiв виконання, i студент, який застосовуi систему, повинен вмiти вибрати найбiльш ефективний варiант. Далi, будь-яка система комп'ютерноi математики не застрахована вiд локальних помилок, i користувач повинен пам'ятати про способи контролю проведених обчислень. Тобто потрiбно, в певному сенсi, вмiти вiдслiдковувати процес виконання перетворень. Також потрiбно мати уявлення про способи подання даних в СКМ.
В данiй курсовiй роботi об'iктом дослiдження i процес вивчення математичного аналiзу.
Предметом дослiдження тАУ використання СКМ Wolfram Mathematica при вивченнi математичного аналiзу.
Мета даноi роботи тАУ продемонструвати можливостi системи Wolfram Mathematica при вивченi математичного аналiзу.
Актуальнiсть роботи полягаi в тому, що за допомогою системи WM, студент може самостiйно перевiряти себе, тобто, контролювати рiвень формування навичок i умiнь, представляти результати у найбiльш наочнiй формi, будувати без труднощiв складнi тривимiрнi поверхнi i т.д. При цьому звiльняти час для обдумування алгоритмiв, бiльш глибокого вивчення математичноi сутностi розв'язуваних задач i iх рiшень рiзними методами.
Для досягнення поставленоi мети визначенi наступнi задачi:
1. розглянути програму навчальноi дисциплiни ВлМатематичний аналiзВ» та самостiйну роботу студентiв по цiй дисциплiнi;
2. розглянути та проаналiзувати сучаснi СКМ;
3. розглянути загальнi вiдомостi про систему Wolfram Mathematica;
4. розглянути особливостi та iнтерфейс системи WM;
5. продемонструвати обчислення границь функцiй у WM;
6. продемонструвати обчислення похiдних i iнтегралiв у WM;
7. продемонструвати побудову графiкiв на плоскостi та у просторi в WM;
8. продемонструвати розкладання функцiй в ряди Тейлора i Маклорена.
9.
Роздiл 1. Теоретичнi аспекти математичного аналiзу та системиWolram Mathematica
1.1 Деякi вiдомостi математичного аналiзу
Математичний аналiз займаi центральне мiсце в ряду математичних i технiчних дисциплiн, якi вивчаються. Вiн i базою, стартовим матерiалом для iх розумiння та засвоювання.
В процесi навчання математичного аналiзу студенти отримують знання та навички як найпростiшого, так i складного аналiзу. Вони вчаться використовувати методи диференцiального та iнтегрального числення функцiй однiii або декiлькох змiнних. Широко ознайомлюються з дослiдженнями функцiй та способами iх представлення, вивчають рiзноманiтнi прийоми та оператори для логiчного та грамотного запису виразiв. Бiльш повний змiст курсу представлений у програмi навчальноi дисциплiни "Математичний аналiз", яка приведена у додатку 1.
Методи математичного аналiзу, заснованi на доказах теорем, лем, наслiдках та iн., привчають студентiв до строгостi математичного мислення, абстрактностi в пiдходах до розвтАЩязання задач, до бачення та прогнозування аналогових ситуацiй. Оволодiння методами математичного аналiзу дозволяi використовувати iх в дослiдницьких та практичних цiлях, домагаючись реальностi результатiв та необхiдноi точностi розрахункiв [6, c. 3].
Мiцне засвоiння сучасних математичних методiв даi змогу випускнику унiверситету розвтАЩязувати в своiй дiяльностi актуальнi практичнi задачi та розумiти написанi на сучасному науковому рiвнi результати iнших дослiдникiв i тим самим удосконалювати свою проф. майстернiсть [6, c. 4].
Однак, курс математичного аналiзу дуже широкий i складний, вiн охоплюi великий обтАЩiм матерiалу. Проте, видiлених годин на практичнi заняття не достатньо для якiсного засвоiння необхiдного матерiалу та для формування навичок i умiнь по цiй дисциплiнi. Тому, приблизно 1/3 вiдводиться на самостiйну роботу студентiв.
Самостiйна навчальна робота не лише формуi у студентiв навички i вмiння самостiйного здобування знань, що важливо для здiйснення неперервноi освiти протягом усiii подальшоi трудовоi дiяльностi, а й маi важливе виховне значення, оскiльки формуi самостiйнiсть як рису характеру, що вiдiграi iстотну роль у структурi особистостi сучасного спецiалiст вищоi квалiфiкацii.
Вагомим пiдТСрунтям для самостiйноi роботи маi стати лекцiя, на якiй викладач не просто закликаi до самостiйноi роботи, а й порушуi проблеми, пропонуi конкретнi завдання, рекомендуi певну лiтературу чи системи комптАЩютерноi математики, визначаi час для виконання роботи, повiдомляi види й термiни ii контролю, наголошуi на можливостi отримати консультацiю [8,c. 126].
Використання СКМ у самостiйнiй роботi студентiв при вивченi математичного аналiзу даi змогу поiднати високi обчислювальнi можливостi з перевагами графiчного подання iнформацii. Це сприяi розвитковi геометричноi iнтуiцii, графiчних навичок, евристичноi дiяльностi студентiв i даi змогу враховувати iхнi iндивiдуальнi здiбностi. Також системи комптАЩютерноi математики можна паралельно використовувати як потужнi електроннi довiдники з великою кiлькiстю прикладiв [8, c. 140].
1.2 Короткий
огляд та аналiз сучасних систем комптАЩютерноi математики
Новi iнформацiйнi технологii докорiнно змiнили порядок вирiшення математичних завдань. Тепер рiшення завдань i виконання математичних перетворень доцiльно проводити за допомогою спецiальних програм. Саме огляду i короткому аналiзу таких програмних продуктiв i присвячений даний пiдроздiл [4, c. 15].
За функцiональнiстю сучаснi математичнi системи дiляться в цiлому на двi категорii: пакети, призначенi в основному для чисельних розрахункiв (MatLab, S-PLUS) i системи комптАЩютерноi алгебри (Derive, Mathematica, Maple, Macsyma, частково, MathCad) тАУ вони також називаються системами символьних чи аналiтичних обчислень (Symbolic Manipulation Program). Це найбiльш унiверсальнi математичнi програми, здатнi вирiшувати най рiзноманiтнi задачi, причому як чисельно, так i точно тАУ аналiтично [11].
Опис та особливостi системи Mathematica будуть розглянутi в пiдроздiлi 1.3.
1) DERIVE
Система Derive, повна назва якоi Derive a Mathematical Assistant (математичний помiчник Derive), фiрми Soft Warehouse, Inc., являiться маловимогливим до ресурсiв пакетом символьноi математики, орiiнтованим в першу чергу на студентiв та шкiльних викладачiв. Однак вiн з успiхом використовуiться також для серйозних наукових дослiджень [3, c. 11].
Derive i зручним iнструментом при диференцiюваннi, iнтегруваннi, розкладаннi функцiй в ряди, знаходженнi границь. Система маi повний набiр вбудованих елементарних функцiй, а також безлiч статистичних i спецiальних математичних функцiй. Система дозволяi працювати з матрицями, проводити перетворення ФуртАЩi i Лапласа. Здатнiсть системи працювати з комплексними числами робить ii привабливою для радiотехнiчних i електротехнiчних розрахункiв. Загалом, можливостi системи повнiстю покривають потреби класичних курсiв елементарноi та вищоi математики [1, c. 23].
2) MAPLE
Даний продукт компанii Waterloo Maple Software, Inc. (http://" onclick="return false">
Проста i ефективна мова-iнтерпретатор, вiдкрита архiтектура, можливiсть перетворення кодiв Maple в коди C робить його дуже ефективним засобом створення нових алгоритмiв. Володii iнтуiтивно зрозумiлим iнтерфейсом, простими правилами роботи i широким функцiоналом, цей продукт вже завоював популярнiсть у росiйських математикiв та iнженерiв. Найближчим конкурентом Maple i пакет Mathematica фiрми Wolfram Research.
3) MATHСAD
Це iнтегроване середовище для виконання, документування та обмiну результатами технiчних обчислень вiд компанii MathSoft, Inc. (http://" onclick="return false">
Система Mathcad спочатку була орiiнтована на чисельнi розрахунки, але в даний час, у звтАЩязку з iнтеграцiiю з Maple, система набула широкi можливостi для символьних перетворень [7, c. 27].
Багато проблем, що виникають при роботi з Mathcad, знiмаються завдяки наявностi електронних пiдручникiв та можливостi пiдключення до глобальноi Мережi РЖнтернет, через яку користувач отримуi доступ до сервера, на якому можна знайти приклад вирiшення подiбного завдання.
4) MACSYMA
Macsyma вiд компанii Macsyma, Inc.( http://" onclick="return false">
Macsyma маi дуже зручний iнтерфейс. Робочим документом програми i науковий зошит, в якому мiстяться доступнi для редагування поля тексту, команд, формул i графiкiв. Вiдмiнною особливiстю пакету i сумiснiсть з текстовим редактором Microsoft Word. Майже всi команди Macsyma в бiблiотечних файлах завантажуються автоматично; дуже зручно i вiкно перегляду (браузер) математичних функцiй. Macsyma генеруi коди FORTRANа i C, включаючи керуючi оператори [10].
5) MATLAB
MATLAB (MATrix LABoratory тАУ матрична лабораторiя) тАУ продукт компанii MathWorks, Inc. (http://" onclick="return false">
В основу створення системи MATLAB покладено принцип розширюваностi, що дозволяi адаптувати систему пiд завдання користувача. Сутнiсть цього принципу полягаi в тому, що користувач може створювати практично необмежену кiлькiсть власних функцiй, якi зберiгаються на жорсткому диску ЕОМ.
Основнi областi застосування MATLAB тАУ це математичнi розрахунки, розробка алгоритмiв, моделювання, аналiз даних i вiзуалiзацiя, наукова та iнженерна графiка, розробка програм, включаючи графiчний iнтерфейс користувача.
Мультиплатформенiсть MATLAB зробила його одним з найпоширенiших продуктiв тАУ вiн фактично став прийнятими в усьому свiтi стандартом технiчних обчислень [10].
Програма MATLAB в основному призначена для чисельного моделювання систем, однак починаючи з версii 5.0 мiстить спецiальний модуль MatLab Notebook для оформлення документiв, а також придбаний модуль символьноi бiблiотеки програми Maple V для виконання аналiтичних перетворень [1, c. 30].
6) S-PLUS
S-PLUS тАУ продукт компанii Insightful Corporation (http://" onclick="return false">
S-PLUS представляi собою iнтерактивне комптАЩютерне середовище, яке забезпечуi повнофункцiональний графiчний аналiз даних i включаi оригiнальну обтАЩiктно-орiiнтовану мову. До основних переваг S-PLUS вiдносяться неперевершена функцiональнiсть, можливiсть iнтерактивного вiзуального аналiзу даних, методи пiдготовки аналiзованих даних, простота використання найсучаснiших статистичних методiв, потужнi обчислювальнi можливостi, розширюваний набiр статистичних методiв i гнучкий iнтерфейс користувача [10].
1.3 Загальнi вiдомостi про систему Wolfram Mathematica
Система Mathematica створена американською компанiiю Wolfram Research, Inc., голова i засновник якоi тАУ вiдомий фiзик i математик Стефан Вольфрам (Stephen Wolfram) тАУ i основним автором розробки. Ще в 70-х роках молодий дослiдник (С. Вольфрам народився в 1959 роцi), працюючи в рiзних галузях фiзики, звернув увагу на те, що вченим дуже часто зустрiчаються схожi комплекси громiздких математичних викладок, якi вiднiмають багато часу. Проводити такi обчислення в той час можна було або Влв лобВ» тАУ озброiвшись ручкою i зошитом, або за допомогою ВлзамовнихВ» комптАЩютерних програм вузькоi спецiалiзацii [12].
Поставивши собi за мету забезпечити вчених продуктивним математичним iнструментом, Вольфрам зiбрав колектив розробникiв для визначення архiтектури новоi (як тепер кажуть, повнiстю ексклюзивноi) комптАЩютерноi системи. Далекоглядна концепцiя системи Mathematica полягало у створеннi раз i назавжди такоi системи символьноi математики, в якiй можна було б обробляти найрiзноманiтнiшi аспекти технiчних обчислень i не тiльки, когерентним i iдиним чином. Ключовим iнтелектуальним досягненням, завдяки якому це стало можливо, стало створення нового виду символiчноi комптАЩютерноi мови, яка вперше змогла манiпулювати найширшим дiапазоном обтАЩiктiв, необхiдних для досягнення унiверсальностi, обовтАЩязкових для технiчних обчислень, використовуючи при цьому лише невелику кiлькiсть примiтивiв [13].
У серпнi 1987 року була заснована Wolfram Research, а наступного року тАУ у червнi 1988 року тАУ офiцiйно вийшла перша версiя системи Mathematica на платформi Macintosh. Програма одразу ж отримала дуже гарнi вiдгуки з боку провiдних (i не тiльки математичних) видань свiту. Ще менш нiж через пiвроку зтАЩявилася версiя Mathematica для комптАЩютерiв з MS-DOS.З тих пiр були розробленi версii системи для Microsoft Windows, Windows NT, OS/2, Linux, Unix, Convex i т.д. тАУ всього бiльше нiж для 20 операцiйних систем i апаратних засобiв.
У 1991 роцi фiрма Wolfram Research представила другу версiю Mathematica, що включаi в себе вдосконалену мову програмування, компiлятор i можливiсть використання готових звукових схем. Третя версiя, випущена в 1996 роцi, представила Mathematica як пакет з новим, простим у використаннi iнтерфейсом з кнопками та палiтрами [13].
Спочатку, вплив системи Mathematica вiдчувався у фiзицi, математицi та iнженерних дисциплiнах. Але з роками, система Mathematica стала активно використовуватися в набагато ширшому дiапазонi областей знань, що виходять за рамки технiчних. Система Mathematica використовуiться сьогоднi в рiзних дисциплiнах тАУ фiзицi, бiологii, соцiальних та iнших науках. Вона зiграла вирiшальну роль у багатьох важливих вiдкриттях i стала основою для тисяч технiчних документiв. У комерцiйнiй дiяльностi система Mathematica граi важливу роль у розвитку складного фiнансового моделювання i в даний час широко використовуiться в багатьох видах загального планування та аналiзу. Система Mathematica також i важливим iнструментом у галузi iнформатики i в розробцi програмного забезпечення тАУ ii мовний компонент широко використовуiться як середовище для проведення дослiджень, написання прототипiв, i в створеннi iнтерфейсiв.
Найбiльша частина користувачiв системи Mathematica складаiться з фахiвцiв технiчних та iнших галузей знань. Однак система Mathematica також широко застосовуiться в освiтi i зараз сотнi курсiв, вiд середньоi школи до аспiрантури, заснованi на ii використаннi. До того ж, пiсля появи студентськоi версii, Mathematica стала популярним i престижним iнструментом для студентiв у всьому свiтi [2, c. 102].
З тих пiр, як була випущена перша версiя Mathematica, кiлькiсть користувачiв системи неухильно зростаi i зараз iх загальна кiлькiсть налiчуi мiльйони. Сьогоднi вона використовуiться всiма компанiями зi списку Fortune 50, в усiх 15-ти департаментах уряду США, i в кожному з 50-ти найбiльших унiверситетах свiту.
Протягом багатьох рокiв спiльнiсть базового дизайну системи Mathematica неухильно дозволяла iй розширювати сфери ii областi впливу. Поступово, система Mathematica пройшла шлях вiд програми, яка використовуiться переважно для математичних та технiчних розрахункiв до iнструменту, широко застосовуваного у рiзних iнших областях обчислювальних дисциплiн [13].
1.4 Особливостi системи Wolfram Mathematica
З перших крокiв i до остаточного результату Mathematica володii швидким та iнтуiтивно-зрозумiлим управлiнням. Mathematica допомагаi швидко просуватися до рiшення при використаннi ii безпосередньо як iнструмент обчислень або ж як потужну систему моделювання.
Для того, хто зiбрався вперше попрацювати з Mathematica, труднощi можуть розпочатися негайно. Все, що система пропонуi при запуску, - це чисте робоче вiкно нового блокнота. Однак досить невеликого досвiду роботи з комптАЩютером, щоб поступово освоiтися i вже незабаром визнати тАУ за широтою охоплення математичного матерiалу, за можливостями оформлення робочих документiв i, особливо, по частинi iнтерфейсу Mathematica як мiнiмум не поступаiться всiм iншим математичним системам разом взятих.
Вбудованi пiдказки й iнтегрована допомога допомагають швидко почати роботу. Вводячи необхiднi числа i символи можна використовувати традицiйну систему запису [9].
Однiiю з особливостей програми i назва стандартних функцiй повними iменами без скорочень. Це дозволяi (при певному рiвнi знання математичноi англiйськоi мови) дуже швидко знаходити потрiбнi функцii.
Mathematica не тiльки може виконувати необхiднi обчислення, але й у багатьох випадках вона вибере оптимальний спосiб проведення обчислень. Все що потрiбно зробити тАУ це визначити завдання; Mathematica ховаi всi складнi механiчнi аспекти вирiшення, дозволяючи концентруватися безпосередньо на завданнi.
Mathematica однаково добре справляiться з завданнями рiзноi складностi i масштабiв, це щось бiльше, нiж звичайна script-мова. Можна сказати, що система Mathematica написана на мовi Mathematica, хоча деякi функцii, особливо повтАЩязанi з лiнiйною алгеброю, з метою оптимiзацii були написанi мовою C [5, c.15].
Система Mathematica складаiться з ядра (обчислювальний механiзм) i зовнiшньоi оболонки (вiзуальний iнтерфейс), якi взаiмодiють через протокол MathLink. Цi компоненти можуть зтАЩiднуватися самими рiзними шляхами. РЖншi компоненти, якi використовують MathLink, можуть мати можливiсть взаiмодiяти з Mathematica.
Бiблiотека програм Mathematica тАУ це постiйно розширювальна збiрка складного програмного забезпечення, яка створена для вирiшення технiчних i обчислювальних завдань для рiзних специфiчних областей. Кожний додаток програми було створено фахiвцем у своiй галузi, який знаi, як застосувати обчислювальнi можливостi Mathematica для вирiшення щоденних завдань [13].
Основнi можливостi системи Mathematica наведенi у додатку 2.
Величезним достоiнством програми Wolfram Mathematica i потужна довiдкова система, яка дозволяi уточнити призначення будь-якоi функцii, оператора або службового слова системи i поступово знайомить з ii можливостями. Однак вона включаi в себе не тiльки дуже якiсний опис функцiй з прикладами, а також пiдручник. У нiй i всi матерiали для тих хто тiльки починаi роботу з програмою, i для тих хто працюi з нею дуже давно. Але i один недолiк тАУ вся програма i довiдкова система написанi виключно англiйською мовою. Тому ця довiдкова система не претендуi на роль навчальноi системи i незручна для знайомства з системою Mathematica [9].
1.5 РЖнтерфейс системи Wolfram Mathematica
Пiсля установки пакета в головному меню створюються ярлики на два файли: Mathematica i Mathematica Kernel. Справа в тому, що ярлик Mathematica Kernel запускаi ядро пакету, яке робить всi обчислення, а ярлик Mathematica запускаi iнтерфейсну частину пакету.
РЖнтерфейс системи Mathematica реалiзуi вiдображення вiкон, палiтр, панелей iнструментiв, знакiв i розташування iх у рiзному виглядi i в рiзних мiсцях екрану монiтора. Типовий робочий вид програми показано на рис.1.4.1. Вiн складаiться з основного меню програми (у верхнiй частинi екрана), вiкна робочого документа або ВлблокнотуВ» (notebook) i панелi (палiтри) для введення _пец символiв i знакiв найбiльш вживаних математичних операцiй (в Mathematica i можливiсть виклику ще шести стандартних панелей, крiм того , користувач сам може створити подiбну панель з набором потрiбних йому _пец символiв i команд) [12].
Основне меню програми мiстить кiлька сотень найменувань пунктiв меню, пiдменю, команд, функцiй. Вивчити iх вiдразу неможливо: з короткого опису не можна зрозумiти змiст. Змiст пунктiв меню, пiдменю, команд можна зрозумiти тiльки в процесi роботи з системою.
Вiкно робочого документа або блокнот складаiться з комiрок. Грубо комiрку можна порiвняти з параграфом у текстовому редакторi. Вся iнформацiя, яка i в блокнотi, зберiгатися в його комiрках. Як тiльки в порожньому новому файлi набираiться хоча б один символ, Mathematica створить для нього комiрку. Комiрка також i мiнiмальною одиницею, яку можна обчислити. Тобто, якщо у комiрцi i двi формули, обчислити iх окремо не вийде. Усi комiрки можна роздiлити на три типи:
тАв комiрки введення тАУ в них задаються команди (формули), якi будуть обчисленi;
тАв комiрки результату тАУ у них Mathematica виводить результат обчислень;
тАв не обчислюванi комiрки тАУ комiрки з текстом, заголовки i все iнше, що вводить користувач i обчислювати не треба [7, c. 59].
Будь-якi клiтинки можна обтАЩiднувати i розбивати за допомогою команд меню Cell: Divide Cell (розбити клiтинку) i Merge Cells (обтАЩiднати комiрки).
Введення даних здiйснюiться в комiрки. Пакет пiдтримуi кирилицю i грецькi лiтери нарiвнi з англiйським алфавiтом. Можна називати змiннi росiйськими лiтерами, також як i грецькими. У той же час, iдентифiкатори розрiзняються по регiстру, тобто змiнна A не те саме, що змiнна a.
Для швидкого доступу до функцiй, розробники Mathematica ввели спецiальнi типи вiкон, якi називаються палiтрами. Палiтри мiстять вiкна з кнопками, якi виконують дii. Дii можуть бути абсолютно рiзними: вiд додавання грецькоi букви, до розкриття дужок у алгебраiчному виразi. Рiзнi палiтри доступнi через меню Palettes. Огляд стандартних палiтр можна знайти у додатку 3 [12].
Wolfram Mathematica маi розвиненi засоби форматування тексту. За допомогою iх можна розбивати блокнот на глави i роздiли, вводити пояснювальний текст i т.д. Стилi можна задати як всьому блокноту, так i окремiй комiрцi цiлком, або частково. Також можна змiнити вiдображення всiх стандартних стилiв i додати новi.
Роздiл 2. Використання системи Wolfram Mathematica при вивченi математичного аналiзу
2.1 Обчислення границь функцii
wolfram mathematica математичний аналiз функцiя
Багато функцiй при наближеннi аргументу до деякого значення або до деякоi областi значень прагнуть до певноi границi. Так, функцiя sin(x)/x при х, яка прагне до нуля (позначимо це як х→ 0), даi границю 1 у виглядi усувноi невизначеностi 0/0.
Чисельнi математичнi системи, так само як i бiльшiсть програм на звичайних мовах програмування, не сприймають вираз 0/ 0 → 1 як об'iктивну реальнiсть. РЗх захисний механiзм налаштований на примiтивне правило - нiчого не можна дiлити на 0. Отже, обчислення sin(x)/x при х = 0 буде супроводжуватися видачею помилки типу ВлДiлення на 0В». Звичайно, в даному конкретному випадку можна передбачити особливий результат тАУ видати 1 при х = 0. Але це окремий випадок. У цiлому ж подiбнi системи Влне розумiютьВ» поняття границi.
У системi Mathematica границi визначаються за допомогою вбудованоi функцii Limit, яка маi вигляд:
Limit [f(х), х → х0],
де:
тАв f (х) - функцiя, границю якоi необхiдно визначити;
тАв х - аргумент функцii f(х);
тАв х0 - граничне значення х.
На рис. 2.1.1 представленi приклади застосування функцii Limit. Ця функцiя дозволяi не тiльки чисельно знаходить границi функцiй, заданих аналiтично, але i дозволяi знайти границю у виглядi математичного виразу. Це свiдчить про високi iнтелектуальнi можливостi системи Mathematica.
При роботi з функцiiю Limit використовуються наступнi опцii:
тАв Analytic тАУ вказуi, чи i невiдома функцiя аналiтичною. Опцiя використовуiться у виглядi Analytic→True (або False), значення за замовчуванням тАУ Automatic. Великого практичного значення ця опцiя не маi;
тАв Direction - вказуi напрямок, в якому вiдбуваiться наближення до границi. Опцiя використовуiться у виглядi Direction→-1 (або +1), за замовчуванням вибiр залишаiться за системою (Automatic). Значення +1 означаi границю лiворуч, а -1 тАУ праворуч (здавалося б, повинно бути навпаки, але задано саме так).
Застосування опцii Direction пояснюють приклади, показанi на рис. 2.1.2.
З прикладiв видно, що границi при наближеннi до них злiва i справа рiзнi. Графiк даi пояснення наближень i вiдповiдей. З графiка видно, що функцiя маi розрив безперервностi i при наближеннi до нього лiворуч (+1), границею буде вiдтАЩiмне значення функцii (-π / 2), i при наближеннi праворуч (-1) тАУ позитивне (π / 2).
2.2 Обчислення похiдних
До числа найбiльш часто використовуваних математичних операцiй належить обчислення похiдних функцiй як в аналiтичнiй, так i в символьнiй формi. Для цього використовуються такi функцii:
тАв D [f, х] тАУ повертаi частинну похiдну функцii f по змiннiй х;
тАв D [f, {х, n}] тАУ повертаi частинну похiдну n-го порядку по х;
тАв D [f, xl, х2 ,..] тАУ повертаi змiшану похiдну;
тАв Dt [f, х] тАУ повертаi узагальнену похiдну функцii f по змiннiй х;
тАв Dt [f] тАУ повертаi повний диференцiал f.
Для функцii D iснуi опцiя NonConstants, яка дозволяi задати список об'iктiв, що знаходяться в неявнiй залежностi вiд змiнних диференцiювання. За замовчанням цей список порожнiй. Для функцii Dt i опцiя Constants, яка, навпаки, вказуi символи, якi i константами (за замовчанням iх список також порожнiй). На практицi застосовувати данi опцii приходиться рiдко.
РЖснуi ще одна функцiя, Derivative [nl, n2 ,..] [f], - основна (загальна) форма подання функцii, отриманоi в результатi nl-кратного диференцiювання функцii f по першому аргументу, n2-кратного - по другому аргументу i т . д.
Приклади застосування функцii D i Dt для обчислення похiдних в аналiтичному виглядi показанi на рис. 2.2.1 й рис. 2.2.2, вiдповiдно.
Приклади на рис. 2.2.3 iлюструють обчислення похiдних вiд першого до третього порядку включно для функцii f[х], заданоi користувачем.
З останнього прикладу видно, що для обчислення вищих похiдних можливе послiдовне застосування функцii D.
У цiлому засоби для символьного обчислення похiдних, якi i в ядрi системи Mathematica, охоплюють практично всi важливi типи математичних виразiв. Вони можуть включати в себе як елементарнi, так i спецiальнi математичнi функцii, що вигiдно вiдрiзняi систему Mathematica вiд деяких простих систем символьноi математики, таких як Derive.
3. Обчислення iнтегралiв
Одна з найважливiших операцiй тАУ обчислення первiсних i визначених iнтегралiв у символьному виглядi. Зауважимо, що визначений iнтеграл може бути представлений як аналiтичним, так i чисельним значенням. Для обчислення чисельних значень визначених iнтегралiв розроблено ряд наближених методiв тАУ вiд простих (прямокутникiв i трапецiй) до складних, якi автоматично адаптуються до характеру змiни пiдiнтегральноi функцii f(x).
Для iнтегрування в системi Mathematica використовуються наступнi функцii:
тАв Integrate [f, x] тАУ повертаi первiсну (невизначений iнтеграл) пiдiнтегральноi функцii f по змiннiй х;
тАв Integrate [f, {x, xmin, xmax}] тАУ повертаi значення визначеного iнтеграла з межами вiд xminдо xmax;
тАв Integrate [f, {x, xmin, xmax}, {у, ymin, ymax },..] тАУ повертаi значення кратного iнтеграла з межами вiд xminдо xmaxпо змiннiй х, вiд yminдо ymaxпо змiннiй у i т. д.
Для бiльш зручного вживання цих функцiй, також як i для похiдноi i границi, iснують кнопки з вiдповiдними значками на палiтрi Basic Math Assistant ![]() .
.
Приклади обчислення невизначених iнтегралiв представленi на рис. 2.3.1.
Тут вхiдна комiрка у першому прикладi представлена у форматi введення (Input-Form), а в iнших прикладах тАУ в стандартному форматi (StandardForm), при використаннi палiтри. При записi iнтегралiв останнiй формат кращий зважаючи на наочностi, оскiльки при цьому знаки iнтеграла мають природний математичний вигляд.
Наступна серiя прикладiв (рис. 2.3.2) iлюструi обчислення визначених iнтегралiв звичайного виду та iнтегралiв з межами-функцiями.
Система Mathematica маi найширшi можливостi обчислення iнтегралiв. Ядро системи увiбрало в себе формули iнтегрування з усiх вiдомих довiдникiв.
Mathematica здатна обчислювати навiть кратнi iнтеграли з фiксованими i змiнними, верхнiм або нижнiм, межами.
На рис. 2.3.3 представлено обчислення декiлькох подвiйних визначених iнтегралiв. Хоча обчислення подвiйного iнтеграла передбачено в синтаксисi функцii Integrate, це не завжди даi результат. Як правило, обчислення кратних iнтегралiв краще виробляти, використовуючи послiдовне обчислення однократних iнтегралiв, вкладених один в одного.
При обчисленнi складних iнтегралiв, наприклад якi не мають представлення через елементарнi функцii, система Mathematica 2 зверталася до своiх пакетiв розширень в спробi знайти рiшення, яке може бути представлене через спецiальнi математичнi функцii. Mathematica наступних версiй вже не акцентуi увагу користувача на своi проблеми i, як правило, видаi результат iнтегрування. Однак деколи вiн може мати досить незвичайний вигляд (рис. 2.3.4).
Цi приклади наочно показують, що обчислення первiсних в системi може дати результати, далекi вiд тривiального обчислення невизначених iнтегралiв, приведених у звичайних довiдниках з математики. До речi, i при обчисленнi тривiальних iнтегралiв результат може бути iншим, нiж у довiдниках, iз-за рiзних перетворень, застосованих для отримання кiнцевих формул. Часом можуть знадобитися певнi зусилля для отримання результату в заданiй формi. Як пiдiнтегральний вираз, так i результати обчислень можуть мiстити як елементарнi, так i спецiальнi математичнi функцii.
Необхiдно зазначити, що результати символьного iнтегрування в системах Mathematica рiзних версiй нерiдко рiзняться. Бiльше того, вони можуть рiзнитися i в межах однiii версii Mathematica, так як ядро системи постiйно вдосконалюiться. Звичайно бiльш пiзнi версii дають бiльш точнi результати обчислень особливих iнтегралiв, хоча часом вони i виглядають бiльш складними i навiть незвичайними. Це говорить про необхiднiсть вдумливо ставитися до одержуваних результатiв.
Для обчислення чисельних значень визначених iнтегралiв використовуiться функцiя NIntegrate [f, {x, xmin, xmax}], яка повертаi чисельне наближення iнтеграла вiд функцii f по змiннiй х в межах вiд xminдо xmax.
Вона маi ряд опцiй, якi можна отримати, виконавши команду Options [Nlntegrate]. Наведемо приклади чисельного iнтегрування (рис. 2.3.5).
Цi приклади показують, що функцiя NIntegrate з успiхом може застосовуватися для обчислення як однократних, так i багатократних визначених iнтегралiв, в тому числi зi змiнними межами.
4. Побудова графiкiв на площинi
У вiдношеннi графiки система Mathematica i лiдером серед систем комп'ютерноi алгебри. Велика кiлькiсть опцiй дозволяi оформляти графiчнi образи практично в будь-якому бажаному виглядi.
Графiки в системi Mathematica i об'iктами i тому вони можуть бути значеннями змiнних.
Почнемо розгляд графiчних можливостей системи з побудови найпростiших графiкiв функцiй однiii змiнноi виду у = f (x) або просто f (x). Графiк таких функцiй будуiться на площинi, тобто в двовимiрному просторi. При цьому використовуiться прямокутна (декартова) система координат. За замовчуванням будуються i лiнii координатноi системи.
Для побудови двовимiрних графiкiв функцiй виду f(x) використовуiться вбудована в ядро функцiя Plot:
Plot [f, {x, xmin, xmax}] тАУ повертаi об'iкт, що представляi собою графiк функцii f аргументу х в iнтервалi вiд xmin до xmax;
Plot [{f1, f2 ,..}, {x, xmin, xmax}] тАУ повертаi об'iкт у виглядi графiкiв ряду функцiй fi.
Функцiя Plot використовуiться для побудови однiii або кiлькох лiнiй, що дають графiчне представлення для зазначених функцiй f, f1, f2 i т. д. Приклади застосування функцii Plot показанi на рис. 2.4.1.Зауважимо, що графiки побудованi без використання будь-яких опцiй (точнiше, з набором опцiй за замовчуванням).
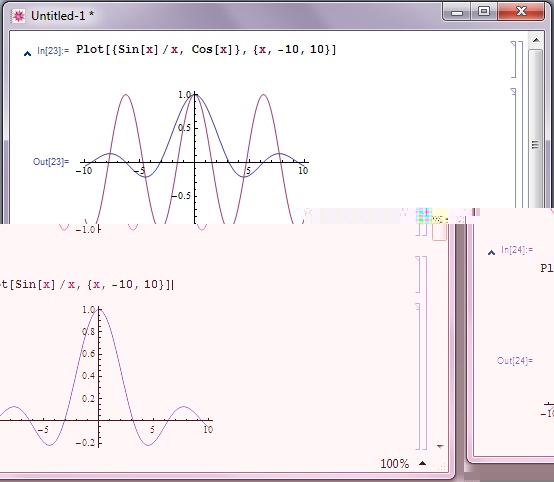
Рис. 2.4.1. Приклади Побудови графiкiв на площинi
В мiру ускладнення задач користувачевi рано чи пiзно перестануть влаштовувати графiки, одержуванi при автоматичному виборi iх стилю та iнших параметрiв. Для точного налаштування графiкiв Mathematica використовуi спецiальнi опцii графiчних функцiй. Для виведення iх списку треба використовувати команду Options [Plot].
Ще одним важливим засобом настроювання графiкiв i графiчнi директиви. Синтаксис iх подiбний синтаксису функцiй. Однак директиви не повертають об'iктiв, а лише впливають на iх характеристики. Застосування графiчних директив спiльно з опцiями дозволяi створювати графiки самого рiзного виду. Так як список опцiй i директив дуже великий, то не будемо на ньому зупинятися.
Також часто виникаi необхiднiсть побудови графiка по точках. Це забезпечуi вбудована в ядро графiчна функцiя ListPlot:
тАв ListPlot [{yl, у2 ,..}] тАУ виводить графiк списку величин. Координати х приймають значення 1, 2, ..;
тАв ListPlot [{{x1, y1}, {х2, у2 },..}]тАУ виводить графiк списку величин з зазначеними х i y координатами.
У найпростiшому випадку (рис. 2.4.2) ця функцiя сама задаi значення координати х = 0, 1, 2, 3, ..i будуi на графiку точки з координатами (х, у), вибираючи у послiдовно зi списку координат. Функцiя ListPlot, особливо в ii другiй формi (iз заданими координатами х i у), зручна для виведення на графiк експериментальних точок.
Система Mathematica також дозволяi будувати графiки функцiй в полярнiй системi координат. Побудова графiкiв в полярнiй системi координат можливо двома способами. Перший спосiб ТСрунтуiться на використаннi звичайноi декартовоi системи координат. Координати кожноi точки при цьому задаються в параметричному виглядi: x = f x(t) i у = f у(t), де незалежна змiнна t змiнюiться вiд мiнiмального значення tmin до максимального tmах. Особливо зручне застосування таких функцiй для побудови замкнутих лiнiй, таких як кола, елiпси, циклоiди i т. д.
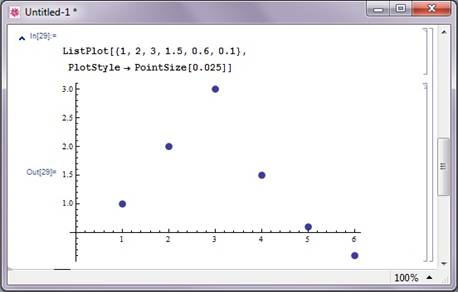
Рис. 2.4.2. Приклад Побудови графiка по точках
Для побудови параметрично заданих функцiй використовуються наступнi графiчнi засоби:
тАв ParametricPlot [{fx, fy}, {t, tmin, tmax}] тАУ будуi параметричний графiк з координатами fх i fу (вiдповiдними х i у), одержуваними як функцii вiд t;
тАв ParametricPlot [{{fx, fy}, {gx, gy },..}, {t, tmin, tmax}] тАУ будуi графiки декiлькох параметричних кривих.
Функцii fx, fу можуть бути як безпосередньо вписанi в список параметрiв, так i визначенi як функцii користувача.
Рисунок 2.4.3 показуi побудову параметрично заданоi фiгури Лiссажу. Вона задаiться функцiями синуса i косинуса з постiйним параметром R i аргументами, кратними t.
Тепер розглянемо другий спосiб побудови графiкiв в полярнiй системi координат (рис. 2.4.4). Для цього використовуiться функцiя PolarPlot:
PolarPlot [f, {t, tmin, tmax}] тАУ будуi графiк в полярнiй системi координа
Вместе с этим смотрят:
РЖнварiантнi пiдпростори. Власнi вектори i власнi значення лiнiйного оператора
Актуальные проблемы квантовой механики
Алгебра и алгебраические системы
Анализ эмпирического распределения
Аналитическая теория чисел. L-функция Дирихле